- Полный квадрат
- Неполный квадрат
- решение уравнений на формулы сокращённого умножения
- Краткое описание документа:
- Математика: теория и методика преподавания в образовательной организации
- Дистанционное обучение как современный формат преподавания
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Тема урока: «Решение линейных уравнений, содержащих формулы сокращенного умножения»
- 🎬 Видео
Формулы сокращённого умножения
Выберите формулы сокращённого умножения, которые записаны правильно.
$a^3 + b^3 = (a + b)(a^2 — ab +b^2)$
$a^3 — b^3 = (a — b)( a^2+2ab + b^2)$
$a^2 — b^2 = a^2 — 2ab + b^2$
$(a + b)^2 = a^2 + 2ab + b^2$
Умножение многочлена
Выполните умножение и вычеркните все неверные ответы $(x — 3)(x^2 +3x+ 9)$.
Произведение многочленов
Установите соответствие, укажите равные выражения.
$(b + 5c)(b^2-5bc + 25c^2)$
$(2b — c)(4b^2 + 2bc +c^2)$
Неполный квадрат
Разделите следующие выражения на две группы.
Полный квадрат
Неполный квадрат
Неверные равенства
Выберите неверные равенства.
$1000 — x^3 = (10 — x)(100 — 10x +x^2)$
$125 — x^3 = (5 — x)( 25 + 10x + x^2)$
$x^3 — 64 = (x — 4)(x^2 + 4x + 16)$
Разность кубов
Разложите на множители $x^3 — 125$.
$(x — 5)(x^2 + 10x + 25)$
Числовое выражение
Зачеркните выражение, которое не делится нацело на 3.
Многочлен
Упростите выражение и введите полученный ответ.
$(b + 7)(b^2 — 7b + 49) — b(b^2 — 5) = b^3 + $ $-b^3 + $ = +
Внимание, знак
Вставьте знак + или – , чтобы равенство было верным.
(a + b)(a 2 ab + b 2 ) = (a 3 b 3 )
(a — b)(a 2 ab + b 2 ) = (a 3 b 3 )
(b — a)(b a) = b 2 a 2
Вычисление значений выражений
Найдите наименьший натуральный делитель числа, отличный от 1.
Преобразование выражений
Упростите выражение и выберите полученный результат из выпадающего списка.
$(4a + 3)(16a^2 — 12a + 9) — a(8a — 5)(8a + 5)$
Разность кубов
Используя формулы сокращённого умножения, решите уравнение и выделите цветом корень уравнения.
$(x — 1)(x^2 + x + 1) + (2 — x)(4 + 2x + x^2)= x$
Решение уравнения
Найдите корень уравнения
$( 2x — 3)( 4x^2 + 6x + 9) + 19 = 0$.
Этапы преобразований
Докажите, что $(3n + 2)^3 + (4n + 5)^3$ делится на 7.
Восстановите последовательность доказательства.
Разложим многочлен на множители, получим:
$(3n + 2 + 4n + 5)$ (Х), где Х неполный квадрат разности
$3n + 2 + 4n + 5 = 7n + 7 = 7(n + 1)$
Делится на 7 так, как один из множителей делится на 7
Видео:7 класс, 24 урок, Формулы сокращённого умноженияСкачать

решение уравнений на формулы сокращённого умножения
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Решение уравнений на формулы сокращённого умножения с построением на плоскости. 7 класс.
1. (х – 7) 2 + 3 = (х — 2) ∙ (х +2)
8. ( 4х – 3)∙(3+4х) – 2х∙(8х – 1) = 0
2. (х +1) ∙ (х +2) – (х — 3) ∙ (х + 4) = 6
9. (3х -1)∙( 2х +7) – ( х+1)∙( 6х – 5) = 7
3. 8 m ∙(1+ 2 m ) – (4 m + 3)∙(4 m – 3) = 2 m
10. х — 3х∙(1 – 12х) = 11 – (5 – 6х)∙(6х + 5)
4. (2х – 3) 2 – 2х∙ (4 + 2х) = 11
11. (2х – 3) 2 – (7 – 2х) 2 = 2
5. (8 – 9а)∙а = — 40 + (6 – 3а)∙(6 + 3а)
12. 24 –( 3у + 1)∙( 4у – 5) = (11 – 6у)∙(2у – 7)
6. ( х + 6) 2 – (х -5)∙(х + 5) = 79
13. ( 6х – 1)∙(6х + 1) – 4х∙(9х + 2) = -1
7. (6у +2)∙(5 –у) = 47–(2у -3)∙(3у – 1)
14. ( 5х – 1) 2 – ( 1 – 3х) 2 = 16х∙(х – 3)
Краткое описание документа:
После того, как изучили формулы сокращённого умножения,решила немного разнообразить работу на уроке и тем самымрешить несколько проблем сразу: повторить решение уравнений, закрепить умение пользоваться формулами на практике, повторение построений на координатной плоскости. Работа заключается в следующем: дети решают уравнения, находят в во втором столбике таблицы ответ и соответствующую ему координату. Затем, по этим координатам они строят фигуру. Учащимся такая работа очень нравится.Они с удовольствием решают уравнения, стараясь быстрее узнать, что за рисунок спрятан. Желаю успеха всем ученикам. которые будут решать эти уравнения.
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 691 человек из 75 регионов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 861 человек из 78 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 51 человек из 23 регионов
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Видео:Формулы сокращенного умножения | Математика | TutorOnlineСкачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 841 044 материала в базе
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 19.02.2015
- 799
- 1
- 19.02.2015
- 503
- 1
- 19.02.2015
- 1550
- 0
- 19.02.2015
- 4071
- 5
- 19.02.2015
- 1962
- 0
- 19.02.2015
- 685
- 0
- 19.02.2015
- 31347
- 327
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 19.02.2015 8791
- DOCX 59.5 кбайт
- 169 скачиваний
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Широкая Ольга Валерьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 7 лет и 3 месяца
- Подписчики: 0
- Всего просмотров: 105282
- Всего материалов: 12
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Решить уравнения, используя формулы сокращенного умножения.Сумма и квадрат разности. Алгебра 7 классСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
С 1 сентября в российских школах будут исполнять гимн России
Время чтения: 1 минута
Инфофорум о буллинге в школе: итоги и ключевые идеи
Время чтения: 6 минут
Около 20% детей до 15 лет не воспринимают прочитанную информацию
Время чтения: 1 минута
Российские школьники начнут изучать историю с первого класса
Время чтения: 1 минута
Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу
Время чтения: 1 минута
В Брянской области часть школ переводят на дистанционное обучение
Время чтения: 0 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Тема урока: «Решение линейных уравнений, содержащих формулы сокращенного умножения»
Разделы: Математика
Цели урока:
- Обработка рациональных приёмов решения уравнений.
- Выработка умения решения задач.
- Развитие элементов творческой деятельности учащихся и умения контролировать свои действия.
- Повторение решения уравнений.
Оборудование: печатные бланки, таблица.
Тип урока: урок- семинар комплексного применения знаний, умений и навыков.
1.Организационный момент. Сообщается план семинара.
2.Сообщение по теме « Уравнение»
3. Решение линейных уравнений.
4.Сообщение о формулах сокращённого умножения.
(Работа у доски и по карточкам.)
а) Решение уравнений, содержащих квадрат суммы.
б) Решение уравнений, содержащих квадрат разности.
в) Решение квадратных уравнений, содержащих разность квадрата.
г) Решение уравнений, содержащих несколько формул.
5. Решение задачи.
6. Творческая работа учащихся.
7. Подведение итогов урока.
Ход урока.
1.Вступительное слово учителя.
Один начинающий волшебник, герой шуточной песенки, неумело обращался с заклинаниями, в результате вместо грозы у него получилась коза, а вместо утюга слон. Чтобы решить уравнение, тоже нужно совершить ряд превращений (алгебраических преобразований) и делать их нужно очень осмотрительно. Сегодня мы ещё раз увидим, какая удивительная сила заключена в формулах сокращённого умножения и как ловко они работают при решении уравнений.
Прежде всего, нужно чётко понимать, чем вы занимаетесь, когда решаете уравнение. Что, значит, решить уравнение и нужно знать, что главная задача при решении любого уравнения — свести его к простейшему.
И сегодня нам будут помогать формулы Сокращённого умножения.
2. Сообщение по теме «Уравнение»
3. Решение линейных уравнений у доски (учащиеся класса записывают решения в тетрадях)
| а) 2-3(x+2)=5-2x; 2-3x-6=5-2x, -3x+2x=5-2+6 -x =9 x=-9 Ответ:-9. | б) 20+4(2x-5)=14x+12 20+8x-20=14x+12, 8x-14x=12, -6x=12, x=-2, Ответ: -2. |
Решение уравнений по карточкам.
в) 4(2-3x)+7(6x+1)-9(9x+4)=30
г) 3-5(x+1)=6-4x.
Сообщение №2.
Слово о формулах.
4. Решение уравнений, содержащих квадрат суммы и квадрат разности.
а) x+(5x+2)2 =25(1+x2).
б) (x-6)2-x(x+8)=2.
Решение уравнений по карточкам.
в) (2-x)2-x(x+1,5)=4
г) x(x-1)-(x-5)2=2.
5. Решение уравнений, в которых содержится формула разности квадратов.
Работа у доски.
8x(1+2x)-(4x+3)(4x-3)=2x.
8x+16×2-(16×2-9)=2x,
8x+16×2-(16×2-9)=2x,
8x+16×2-16×2+9=2x,
8x-2x=-9,
6x=-9,
x=-1,5
Ответ: -1,5
Решение задачи.
Сторона первого квадрата на 2см. больше стороны второго, а площадь первого на 12 см больше площади второго. Найдите периметры этих квадратов.
Пусть x см сторона второго квадрата. Тогда(x+2) см сторона первого квадрата. Площадь первого (x+2) 2 см 2 ,а площадь второго x 2 .
Составляем уравнение:
(x+2) 2 -x 2 =12
x 2 +4x+4-x 2 =12,
4x=12-8,
4x=8,
x=2.
Если x=2,то 4x=4*2=8
Если x=2, то 4(x+2)=4(2+2)=16.
Ответ:16см,8см.
6. Решение разных уравнений, содержащих формулы сокращённого умножения.
7.Творческая работа учащихся. Заполнение таблицы.
Узнайте фамилию величайшего математика XVII века. Для этого зачеркните
буквы, не связанные с найденными ответами.
(Декарт)
| -9 | 8,2 | -2 | 3,4 | 1 | 3,1 | 1,7 | 15 | -1,5 | 17 | 11 | 3 |
| Д | П | Е | Ф | К | С | А | И | Р | Г | Ш | Т |
Приложение к уроку.
Решение линейных уравнений.
| 4(2-3x)+7(6x+1)-9(9x+4)=30 8-12x+42x+7-81-36=30, 51x-21=30, 51x=51 x=1 Ответ: 1. | 3-5(x+1)=6-4x, 3-5x-5=6-4x, -5x+4x=6-3+5, -x=8x= -8. Ответ:-8. |
Решение уравнений, содержащих квадрат суммы и квадрат разности.
| x+(5x+2) 2 =25(1+x 2 ) x+(25x 2 +20+4)=25(1+x 2 ) x+25x 2 +20x+4=25+25x 2 , 21x+25x 2 -25x 2 =25-4, 21x=21 x=1 Ответ:1. | (x -6) 2 -x(x+8)=2 x 2 -12x+36-x 2 -8x=2 -20x=2-36, -20x=-34, x=1,7 Ответ: 1,7. |
Работа по карточкам.
| (2-x)2-x(x+1,5)=4, 4-4x+x 2 -x 2 -1,5x=4, -4x-1,5x=4-4, -5,5 x=0 Ответ:0. | x(x-1)-(x-5) 2 =2 x 2 -x-(x 2 -10x+25)=2, x 2 -x-x 2 +10x-25=2 9x=27 x=3 Ответ: 3. |
Решение разных уравнений содержащих несколько формул сокращённого умножения.
| (x-4x)+(x+4)+(3x-4)(x+2)=(2x+3) 2 x 2 -16+3x 2 +6x-4x-8=4x 2 +12x+9 -10x=33 x=-3,3 Ответ:3,3. | ( 2x+3)2-4(x-1)(x+1)=49 4x 2 +12x+9-4(x 2 -1)=49 4x 2 +12x+9-4x 2 +4=49 12x+13=49 12x=36 X=3 Ответ: 3. |
8. Подведение итогов урока.
🎬 Видео
Квадрат суммы и квадрат разности двух выражений. 7 класс.Скачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Вычисления. Корни. Преобразования. Формулы сокращенного умножения.Скачать

Алгебра 7. Урок 4 - Формулы сокращенного умножения и как их запомнить.Скачать

Решение уравнений с формулами сокращенного умножения, 7 классСкачать

Формулы сокращенного умножения #математика #алгебра #формулы #шпаргалкаСкачать

Разность квадратов двух выражений. 7 класс.Скачать

#110 Урок 35. Вычисление значений корня при помощи формул сокращенного умножения. Алгебра 8 класс.Скачать

Решите уравнение ➜ (x²-x-1)²-x³=5 ➜ Задача от подписчикаСкачать

Формула сокращенного умноженияСкачать

Алгебра 7 класс с нуля | Математика | УмскулСкачать

Как раз и навсегда выучить формулы сокращенного умноженияСкачать
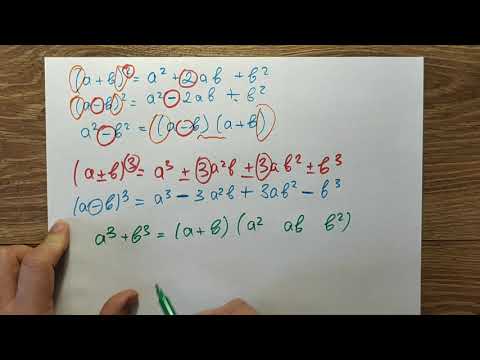
Формула сокращённого умноженияСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Алгебра 7 класс – Квадрат суммы и разности – ФСУ часть 1Скачать




