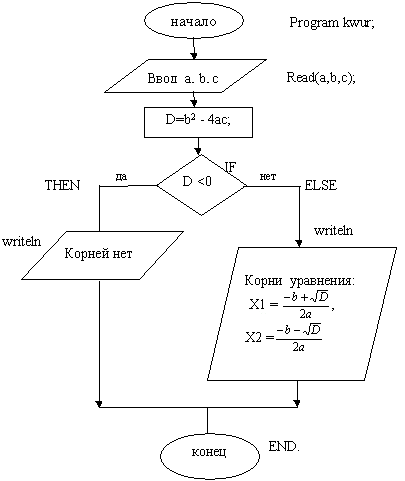
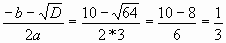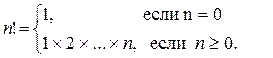Алгоритм решения данной задачи сначала должен быть представлен в виде словесного описания или графически в виде блок-схемы. Алгоритм вычисления корней квадратного уравнения может быть представлен в виде блок-схем, изображенных на рисунках, отображающих основные элементы блок-схем и алгоритм вычисления корней квадратного уравнения:
Изображение алгоритма в виде блок-схемы позволяет наглядно представить последовательность действий, необходимых для решения поставленной задачи, убедиться самому программисту в правильности понимания поставленной задачи.
После разработки алгоритма решения задачи и представления его в виде блок-схемы можно перейти к написанию программы – последовательности инструкций на выбранном языке программирования, соответствующей разработанному алгоритму. Например, ниже приведен фрагмент программы решения квадратного уравнения, соответствующий приведенному выше алгоритму, составленному на языке Visual Basic.
procedure SqRoot(Editi,Edit2,Edit3:tEdit;Label2:tLabel);
var
a,b,c:real;
d:real;
xl,x2:real;
begin
a:=StrToFloat(Editl.text);
b:=StrToFloat(Edit2.text);
с:=StrToFloat(Edj.t3.text);
d:=Sqr(b)-4*a*c;
if d=0 then begin
Label2.color:=clRed;
Label2.font.color:=clRed;
Label2.caption:=’Дискриминант меньше нуля.’+#13+
‘Уравнение не имеет корней.’ end else
begin
х1:=(-b+Sqrt(d))/(2*a);
x2:=(-b-Sqrt(d))/(2*а);
Label2.font.color:=clBlack;
Label 2.caption=’Корни уравнения:’ +#13+’xl=1+FloatToStr(xl)
+#13+’x2=’+FloatToStr(x2);
end;
end.
Но программа, написанная на языке программирования, состоит из инструкций, понятных человеку, но не понятных процессору компьютера. Поэтому чтобы процессор смог выполнить работу в соответствии с инструкциями исходной программы, она должна быть переведена на язык команд процессора, то есть машинный язык. Задачу преобразования исходной программы в машинный код выполняет специальная программа — компилятор. Помимо преобразования исходной программы в машинную, компилятор выполняет проверку правильности записи инструкций исходной программы, т. е. осуществляет синтаксический анализ.
Компилятор создает исполняемую программу только в том случае, если в тексте исходной программы нет синтаксических ошибок. Однако генерация исполняемой программы машинного кода свидетельствует только об отсутствии в тексте программы синтаксических ошибок. Убедиться в правильности работы программы можно только во время ее тестирования – пробных запусках программы и при анализе полученных результатов. Например, если в программе нахождения корней квадратного уравнения допущена ошибка в записи выражения вычисления дискриминанта, то даже если это выражение будет синтаксически верно, программа выдаст неверные значения корней.
Решение квадратных уравнений средствами Visual Basic
Задача: Дано квадратное уравнение общего вида: ax 2 +bx+c=0. Ввести в память компьютера числовые коэффициенты: a, b, c, выполнить необходимый анализ введенной информации согласно известному из курса средней школы алгоритму решения квадратного уравнения: найти дискриминант d=b 2 -4ac и, проанализировав его знак, найти все действительные корни, если знак дискриминанта положительный, или сообщить о том, что действительных корней нет, если знак дискриминанта отрицательный.
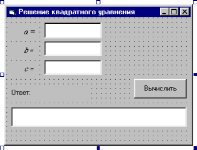
Начать составление проекта решения данной задачи необходимо с ответа на вопрос: что нужно поместить на форму Form1?
Поместим на форму две кнопки: CommandButton1 и CommandButton2.
Для этого нужно воспользоваться Панелью элементов (объектов) управления General, которая расположена в левой части основного окна компилятора Visual Basic.
Первая кнопка CommandButton1 предназначается для начала работы программы согласно следующему алгоритму:
- ввод коэффициентов исходного уравнения a, b, c;
- расчет дискриминанта d=b 2 — 4ac;
- анализ знака дискриминанта, вычисление корней уравнения и вывод их на форму, если знак дискриминанта d>0 (положительный);
- вывод сообщения: «Решений нет», если знак дискриминанта d 2 -5x+6=0.
Далее рассмотрим процесс решения второго квадратного уравнения: 10x 2 +5x+200=0.
В окне InputBox вводим значение первого коэффициента уравнения a=10.
Ввод первого коэффициента a завершается нажатием кнопки Ok.
Аналогично в окне InputBox вводим значение второго коэффициента уравнения b=5.
Ввод второго коэффициента b так же завершается нажатием соответствующей кнопки Ok.
Наконец, в окне InputBox вводим значение третьего коэффициента нового уравнения c=200.
Ввод третьего коэффициента c так же завершается нажатием соответствующей кнопки Ok.
После этого программа, проанализировав полученную информацию, должна выдать в окне формы соответствующее сообщение о том, что данное уравнение не имеет решений.
И, наконец, рассмотрим процесс решения третьего квадратного уравнения: x 2 -8x+16=0.
Это уравнение имеет двукратный корень, так как его дискриминант d=0. Как и в двух предыдущих случаях, вводим коэффициенты квадратного уравнения. Первым вводим коэффициент a=1.
Далее вводим второй коэффициент уравнения b= –8.
Третий коэффициент уравнения c=16 вводим в последнюю очередь.
В итоге мы должны увидеть правильное решение третьего квадратного уравнения. Действительно последнее уравнение имеет два одинаковых корня.
- Составьте блок схему нахождение корней квадратного уравнения ax2 + bx + c = 0?
- Составить блок — схему нахождения квадрата числа?
- Составьте блок — схему алгоритма поиска корней квадратного уравнения ax2 + bx + c = 0?
- Начертите блок схемы?
- Помогите составить план алгоритма (блок схема)1 задача?
- Составьте блок — схему алгоритма нахождения х уравнения 2х + а = с ?
- Составить алгоритм нахождения квадратов, кубов и корней целых чисел от1 до 100(блок – схема)?
- Составьте блок схему решения уравнения ax = b?
- Помогите написать программный код для решения квадратного уравнения в Паскале с блок схемой?
- Составить блок схему алгоритма нахождения знакочередующейся суммы?
- Составьте блок — схему и программу для нахождения суммы квадратов всех нечетных чисел в интервале от 30 до 80?
- Составить блок схему алгоритма решения квадратного уравнения
- Visual basic практическая работа «Решение квадратного уравнения»
- Просмотр содержимого документа «Visual basic практическая работа «Решение квадратного уравнения»»
- 🎥 Видео
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Составьте блок схему нахождение корней квадратного уравнения ax2 + bx + c = 0?
Информатика | 10 — 11 классы
Составьте блок схему нахождение корней квадратного уравнения ax2 + bx + c = 0.
Смотри во вложении_______________.
Видео:Блок-схемы для начинающих (Блок схемы алгоритмов)Скачать

Составить блок — схему нахождения квадрата числа?
Составить блок — схему нахождения квадрата числа!
Видео:0.Блок схема. 8 классСкачать

Составьте блок — схему алгоритма поиска корней квадратного уравнения ax2 + bx + c = 0?
Составьте блок — схему алгоритма поиска корней квадратного уравнения ax2 + bx + c = 0.
Видео:Алгебра 8 класс (Урок№28 - Решение квадратных уравнений вида ax2 + bx + c = 0.Формула корней кв.ур.)Скачать

Начертите блок схемы?
Начертите блок схемы.
Задача : составьте алгоритм нахождения большего из четырех чисел a, b, c, d?
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Помогите составить план алгоритма (блок схема)1 задача?
Помогите составить план алгоритма (блок схема)
Вычислить длину окружности
Вычисление корней квадратного уравнения через дискриминант.
Видео:Решаем задачи в виде блок-схемы (7 класс)Скачать

Составьте блок — схему алгоритма нахождения х уравнения 2х + а = с ?
Составьте блок — схему алгоритма нахождения х уравнения 2х + а = с .
Выполните его при : а) а = 5 , с = 7.
; б) а = — 15 , с = 105 ; в) а = 5 , с = 5.
Видео:Самый подробный урок про Блок-схемы, Понимание, Чтение и Создание блок-схемСкачать

Составить алгоритм нахождения квадратов, кубов и корней целых чисел от1 до 100(блок – схема)?
Составить алгоритм нахождения квадратов, кубов и корней целых чисел от1 до 100(блок – схема).
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Составьте блок схему решения уравнения ax = b?
Составьте блок схему решения уравнения ax = b.
Видео:Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать

Помогите написать программный код для решения квадратного уравнения в Паскале с блок схемой?
Помогите написать программный код для решения квадратного уравнения в Паскале с блок схемой.
Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

Составить блок схему алгоритма нахождения знакочередующейся суммы?
Составить блок схему алгоритма нахождения знакочередующейся суммы.
Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Составьте блок — схему и программу для нахождения суммы квадратов всех нечетных чисел в интервале от 30 до 80?
Составьте блок — схему и программу для нахождения суммы квадратов всех нечетных чисел в интервале от 30 до 80.
Если вам необходимо получить ответ на вопрос Составьте блок схему нахождение корней квадратного уравнения ax2 + bx + c = 0?, относящийся к уровню подготовки учащихся 10 — 11 классов, вы открыли нужную страницу. В категории Информатика вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.
2 Мбайта = 2048 килобайт = 2097152 байт.
1мегабайт = 1024 байт значит : 2кб = 20 48 байт.
Интернет символ «@»появилсянесколько сотен лет назад всредневековых монастырях. Его использовали для обозначения латинского предлога «ad» (всовременном английском— «at»), хотя некоторые исследователи утверждают, что «собаку» придумали итальянские мо..
Американский ученый Бертольд Уллман выдвинул предположение, что знак @ был изобретен средневековыми монахами для сокращения латинского слова «ad», которое часто употреблялось в качестве универсального слова, означающего «на», «в», «в отношении» и т. ..
Видео:Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать

Составить блок схему алгоритма решения квадратного уравнения
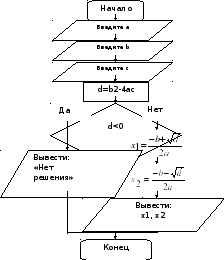
Задача 1. Составить блок-схему и программу, находящие корни квадратного уравнения
ПРОГРАММА на БЕЙСИК
PRINT “Решение квадратного уравнения“
INPUT “Ввести a, b, c: “, a, b, c
d = b * b – 4 * a * c
THEN Х 1=(-b-sqr(d))/(2*a) : Х 2=(-b+sqr(d))/(2*a) : PRINT “Х1=“, Х1, “ Х2=“, Х2
ELSE PRINT “Действительных корней нет “
Запустите программу на выполнение и решите следующие квадратные уравнения:
а) 1125 х 2 – 45 х – 324 = 0
б) 502 х 2 – 38,5 х + 12,125 = 0
в) 16 х 2 – 256 х + 1024 = 0
Задача 2. Составить блок-схему и программу, определяющие количество корней квадратного уравнения

ПРОГРАММА на БЕЙСИК
PRINT “Количество корней квадратного уравнения“
INPUT “Ввести a, b, c: “, a, b, c
d = b * b – 4 * a * c
IF d > 0 THEN PRINT “2 разных корня“ ELSE PRINT “2 одинаковых корня“
ELSE PRINT “Действительных корней нет“
Запустите программу на выполнение и определите количество корней в следующих квадратных уравнениях:
а) 1125 х 2 – 45 х – 324 = 0
б) 502 х 2 – 38,5 х + 12,125 = 0
в) 16 х 2 – 256 х + 1024 = 0
Задача 3*. Составить блок-схему и программу, определяющие имеет ли квадратное уравнение ax 2 + bx + c = 0 хотя бы один корень, больший числа m .
Запустите программу на выполнение и определите имеется ли корень в следующих квадратных уравнениях:
а) 1125 х 2 – 45 х – 324 = 0 при m = 0
б) 502 х 2 – 38,5 х + 12,125 = 0 при m = 15
в) 16 х 2 – 256 х + 1024 = 0 при m = 7
Домашнее задание – Составить блок-схемы и программы для следующих задач:
Задача 1. Определить является ли введенное с клавиатуры число корнем квадратного уравнения ax 2 + bx + c = 0 .
До сих пор мы с вами говорили о каких-то отвлечённых задачах из области математики. Сегодня мы поговорим о конкретной задаче, которая встречается у вас почти на каждом уроке. Это решение квадратного уравнения. Я хочу, чтобы вы на примере этой задачи поняли, что программирование – это не просто прихоть учителя, это действительно раздел информатики, который может нам помочь, например, в решении конкретных математических задач. Нужно только уметь разбираться в этом.
2. Математическое решение
Давайте вспомним, что понимают под квадратным уравнением?
Что из себя представляют числа a,b,c и как их называют?
С чего начинают решение квадратного уравнения?
Найдите вокруг себя формулу дискриминанта. (D=b 2 -4ac) (Приложение 3)
Как мы решаем далее квадратное уравнение? (сравнение D с нулём)
Какие выводы мы из этого делаем?
(если D 0, то два корня)
Как найти корни квадратного уравнения? Найдите формулы корней среди тех, что развешены повсюду.
Если я случай наличия корней квадратного уравнения сведу к условию D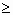
(Два одинаковых корня)
Давайте ещё раз подробно разберём нашу задачу:
Итак, у нас есть квадратное уравнение ax 2 +bx+c=0.
Мы должны решить его, т.е. найти такие значения х, при которых правая часть уравнения =0. Мы знаем, что для этого нам надо:
Найти дискриминант D=b 2 – 4ac.
Сравнить его с нулём
D=b 2 -4ac=10 2 -4*3*3=100 – 36 =64
Х1=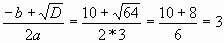
X2 =
3. Составление блок-схемы алгоритма.
По заданному решению попробуем составить блок-схему алгоритма в тетради. Кто справится первым, прошу к доске.
Подпишем основные элементы блок – схемы применительно к языку программирования.
4. Составление программы по блок – схеме.
Теперь, пользуясь нашими записями, составим программу и покажем её учителю. Тот, кто до конца урока составит только программу, не проверив её на компьютере, получит три, тот, кто наберёт программу на компьютере, но не проверит её на примерах, получит три. Тот, кто выполнит всё задание, получит пять.
А я раздам вам домашнее задание.
Var a,b,c,d,x1,x1: real;
Write(‘введите коэффициенты уравнения a,b,c’); readln(a,b,c);
Else writeln(‘действительных корней нет’)
1. Составить и набрать программу КВУР на компьютере.
Загрузка среды Pascal- 2ЩЛКМ по значку Pascal, нажать ALT+ENTER.
Запуск программы – ЩЛКМ по кнопке RUN выбрать RUN.
2. Решить следующие квадратные уравнения и показать учителю их решения (если нет такой возможности, то занести их в маршрутный лист (Приложение 4)
1,5х 2 -0,6х – 4,8 = 0
3. Переделайте программу КВУР таким образом, чтобы в ней учитывался случай, когда D=0 и уравнение имеет один корень.
4. Закрыть программу.
Подсказка: Меню File – Exit или ALT+X.
1. За простое воспроизведение (набор программы) без проверки оценка “3”
2. За проверку работы программы на примерах, представленных учителем оценка “4”
3. За решение всех заданий и дополнительное изменение программы для случая D=0, оценка “5”
4. Закрыть программу.
Подсказка: Меню File – Exit или ALT+X.
| № | Х1 | Х2 |
| 1 | 3,230139 | 0,1031947 |
| 2 | 1,464102 | -5,464102 |
| 3 | 1,106107 | -1,356107 |
| 4 | Корней нет | |
| 5 | Корней нет | |
| 6 | 1,6 | |
| 7 | 2 | -1,6 |
| 8 | Корней нет | |
| 9 | 0,6872614 | -1,131706 |
| 10 | 9,486833 | -9,486833 |
Можно дать дополнительное задание:
Изменить программу так, чтобы ответ был с точностью до 2-х знаков после запятой.
1) Напишите программу проверки пароля. Пусть пароль – некоторое число, зафиксированное в программе. Программа печатает приглашение «введите пароль» и вводит число. Если введённое число совпадает с фиксированным паролем, то программа выводит приветствие, если нет – сообщает о том, что пароль не угадан.
7. Подведение итогов урока.
Итак, ребята, сегодня мы с вами решали конкретные задачи из математики, применяя свои умения по программированию. Вы получили следующие оценки за свои знания. (Перечисление оценок) На следующем уроке нам предстоит познакомиться с новыми алгоритмами – Циклическими.
На сегодня наш урок закончен. До свидания.
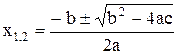 |
Задача хорошо знакома из математики. Исходными данными здесь являются коэффициенты a, b, c. Решением в общем случае являются два корня x1 и x2, которые вычисляются по формулам:
Все величины, используемые в этой программе, имеют вещественный тип.
алг корни квадратного уравнения
вещ a, b, c, x1, x2, d
начввод a, b, c
Кон
Слабость такого алгоритма видна «невооруженным глазом». Он не обладает важнейшим свойством, предъявляемым к качественным алгоритмам: универсальностью по отношению к исходным данным. Какими бы ни были значения исходных данных, алгоритм должен приводить к определенному результату и выходить на конец. Результатом может быть числовой ответ, но может быть и сообщение о том, что при таких данных задача решения не имеет. Недопустимы остановки в середине алгоритма из-за невозможности выполнить какую-то операцию. Это же свойство в литературе по программированию называют результативностью алгоритма (в любом случае должен быть получен какой-то результат).
Чтобы построить универсальный алгоритм, сначала требуется тщательно проанализировать математическое содержание задачи.
Решение уравнения зависит от значений коэффициентов a, b, c. Вот анализ этой задачи (ограничиваемся только поиском вещественных корней):
если a=0, b=0, c=0, то любое х – решение уравнения;
если a=0, b=0, c¹0, то уравнение решений не имеет;
если a=0, b¹0, то это линейное уравнение, которое имеет одно решение: x=–c/b;
если a¹0 и d=b 2 -4ac³0, то уравнение имеет два вещественных корня (формулы приведены выше);
кв
кв
Кон
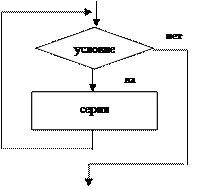
В этом алгоритме многократно использована структурная команда ветвления. Общий вид команды ветвления в блок-схемах и на алгоритмическом языке следующий:
 |
Вначале проверяется «условие» (вычисляется отношение, логическое выражение). Если условие истинно, то выполняется «серия 1» – последовательность команд, на которую указывает стрелка с надписью «да» (положительная ветвь). В противном случае выполняется «серия 2» (отрицательная ветвь). В АЯ условие записывается после служебного слова «если», положительная ветвь – после слова «то», отрицательная – после слова «иначе». Буквы «кв» обозначают конец ветвления.
Если на ветвях одного ветвления содержатся другие ветвления, то такой алгоритм имеет структуру вложенных ветвлений. Именно такую структуру имеет алгоритм «корни квадратного уравнения». В нем для краткости вместо слов «да» и «нет» использованы соответственно «+» и «–».
Рассмотрим следующую задачу: дано целое положительное число n. Требуется вычислить n! (n-факториал). Вспомним определение факториала.
Ниже приведена блок-схема алгоритма. В нем используются три переменные целого типа: n – аргумент; i – промежуточная переменная; F – результат. Для проверки правильности алгоритма построена трассировочная таблица. В такой таблице для конкретных значений исходных данных по шагам прослеживается изменение переменных, входящих в алгоритм. Данная таблица составлена для случая n=3.
 |
Трассировка доказывает правильность алгоритма. Теперь запишем этот алгоритм на алгоритмическом языке.
алгФакториал
целn, i, F
нач ввод n
F:=1; i:=1
пока i£n, повторять
нц F:=F´i
кц
Кон
Этот алгоритм имеет циклическую структуру. В алгоритме использована структурная команда «цикл-пока», или «цикл с предусловием». Общий вид команды «цикл-пока» в блок-схемах и в АЯ следующий:
 |
Повторяется выполнение серии команд (тела цикла), пока условие цикла истинно. Когда условие становится ложным, цикл заканчивает выполнение. Служебные слова «нц» и «кц» обозначают соответственно начало цикла и конец цикла.
Цикл с предусловием – это основная, но не единственная форма организации циклических алгоритмов. Другим вариантом является цикл с постусловием. Вернемся к алгоритму решения квадратного уравнения. К нему можно подойти с такой позиции: если a=0, то это уже не квадратное уравнение и его можно не рассматривать. В таком случае будем считать, что пользователь ошибся при вводе данных и следует предложить ему повторить ввод. Иначе говоря, в алгоритме будет предусмотрен контроль достоверности исходных данных с предоставлением пользователю возможности исправить ошибку. Наличие такого контроля – еще один признак хорошего качества программы.
 | алгквадратное уравнение вещa, b, c, d, x1, x2 нач повторять ввод a, b, c до a¹0 d:=b 2 –4ac если d³0 тоx1:=(–b+Öd)/(2a) x2:=(–b–Öd)/(2a) вывод x1, x2 иначе вывод “нет вещественных корней” кв кон |
В общем виде структурная команда «цикл с постусловием» или «цикл-до» представляется так:
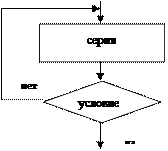 |
Здесь используется условие окончания цикла. Когда оно становится истинным, цикл заканчивает работу.
Составим алгоритм решения следующей задачи: даны два натуральных числа M и N. Требуется вычислить их наибольший общий делитель – НОД(M,N).
Эта задача решается с помощью метода, известного под названием алгоритма Евклида. Его идея основана на том свойстве, что если M>N, то НОД(M N то M:=M–N иначе N:=N–M кв кц кон
Алгоритм имеет структуру цикла с вложенным ветвлением. Проделайте самостоятельно трассировку этого алгоритма для случая M=18, N=12. В результате получится НОД=6, что, очевидно, верно.
Видео:Блок-схема циклического алгоритма. Вычисление n!Скачать

Visual basic практическая работа «Решение квадратного уравнения»
Решение квадратного уравнения на языке VB в двух вариантах и рассмотрение блок-схемы решения задачи.
Просмотр содержимого документа
«Visual basic практическая работа «Решение квадратного уравнения»»
Лабораторная работа №1. Решение квадратного уравнения.
1. Вывод результата с помощью оператора Print
Решение. Рассмотрим блок-схему решения данной задачи:
Программа написана справа от блок-схемы.
Private Sub Command1_Click()
d = b * b — 4 * a * c
X1 = (-b + Sqr(d)) / (2 * a)
X2 = (-b — Sqr(d)) / (2 * a)
Для выполнения программы нажимает клавишу F5. Вводим значения коэффициентов a, b, c. Результат работы программы читаем в форме.
a=1567, b = -110, c = -15, ответ: x1=0,13904296372987 x2=-6,88451334809872E-02
При вводе десятичных дробей через окно InputBox следует применять запятую.
a=1,5, b = 1, c = -4, ответ: x1 = 1,3333333, x2 = -2
Если запустить программу и ничего не вводить (a=0, b = 0, c = 0), а нажимать ОK (Enter), то появится сообщение об ошибке. Следует нажать кнопку End.
2) Добавление новых элементов в форму
Главным объектом среды программирования Visual Basic является форма. До сих пор на форме мы располагали только одну кнопку, результат читали также на поверхности формы.
Инструментальное меню Visual Basic содержит много элементов, которые также можно разместить на форме. Познакомимся поближе со второй строкой этой панели.
Буква А означает надпись. При наведении на неё курсора появляется слово Label (читается лэйбл, переводится этикетка, надпись). На форме надпись будет растягиваться аналогично командной кнопке — в виде прямоугольника. В неё мы будем печатать поясняющие надписи.
Справа от неё находится кнопка текстовое окно TextBox (читается ТекстБокс, текстовая панель). В текстовое окно можно вводить и выводить информацию (числа, слова).
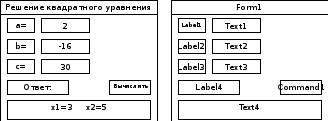
Создадим форму для задачи «Нахождение корней квадратного уравнения», используя вышеперечисленные элементы инструментального меню. Прежде всего создадим в тетради эскиз формы. Он может выглядеть так:
Создадим на форме места под будущие надписи и окна. Методом растягивания, перетаскивания и изменения размеров создайте форму с кнопкой, четырьмя лейблами, и четырьмя текстовыми окнами.
Изменение свойств формы
Щелкнем на свободном месте формы. Она будет ограничена квадратными маркерами по восьми направлениям изменения размеров формы.
Справа активизировалась панель свойств этой формы – Properties – Form1 (читается пропетиз фом ван, переводится свойства формы один). В этом окне слева расположены названия свойств, а справа их значения. Значения мы можем менять по своему усмотрению. Названия свойств являются ключевыми словами языка VB, их постепенно надо запоминать. Нам надо изменить текст в заголовке формы. Изменение текста заголовка формы выполняется в строке Caption (произносится — кэпшн, переводится заголовок). Щелкаем мышкой по этому свойству, печатаем – Решение квадратного уравнения, нажимаем Enter. Текст появляется в заголовке формы.
Изменим цвет формы. Для этого в свойствах находим строку BackColor (бэк колор, задний цвет). На вкладке Palette (палетте, палитра) выбираем нужный нам цвет для формы, щелкнув по нему указателем мыши.
Выделяем командную кнопку и в разделе свойств Caption печатаем Вычислить.
Выделяет объект Label1. В разделе свойств Caption печатаем а =. Переходим к свойству Alignment (читается — элайнмент, переводится выравнивание). Раскрываем список этой строки и выбираем выравнивание по правому краю 1. Right Justify (Райт джустифай, правое, если много текста, то левая и правая границы выровнены). Можно было нажать клавишу с цифрой 1.
Свойство Font (фонт, вид шрифта) позволит нам настроить вид символов. В диалоговом окне можно выбрать тип шрифта, начертание (обычный, курсив, полужирный) и размер 14. Сделайте так, чтобы текст а = выглядел как а =. “это достигается применением шрифта Times New Roman (Таймс Нью Роман)
Аналогично меняем содержимое объектов Label2, Label3.
В свойстве Caption объекта Label4 записываем Ответ:
В свойствах текстового окна Text1 находим строку Text. Стираем существующую надпись, можно пробелом, и подтверждаем изменение клавишей Enter или щелчком мыши на другом объекте.
Аналогично поступаем с остальными текстовыми окнами. Форма готова.
Точечная запись — в качестве переменной
Объектно-ориентированные языки программирования работают с объектами. В качестве объекта может быть форма, командная кнопка, надпись, текстовое окно и др. Каждый из этих объектов имеет свойства. Эти свойства можно менять по нашему усмотрению либо на Панели свойств (Properties), либо из программы. Для того, чтобы изменить свойства из программы, точнее, иметь доступ к свойствам объекта их командной строки, нужно указать название объекта и через точку свойство. Например, чтобы иметь доступ к содержимому первого текстового окна нашего проекта по свойству Text, надо сделать запись: Text1.Text. –(в программном коде)
Такая запись может использоваться в качестве переменной. Свойство может содержать какое-либо значение. Это значение мы можем записать при запуске программы, или программист, при составлении программы, поместит в него какое-нибудь значение.
Сравните две строки:
Text1.Text = “5” — эта строка помещает значение 5 в текстовое окно Text1.
a= Text1.Text — эта строка присваивает переменной a содержимое текстовой строки. Если в текстовом окне ничего нет, то Visual Basic помещает в него специальное значение Null. Это ни нуль, не пробел, а пустое место.
для этой формы будет выглядеть так:
Private Sub Command1_Click()
d = b * b — 4 * a * c
X1 = (-b + Sqr(d)) / (2 * a)
X2 = (-b — Sqr(d)) / (2 * a)
Text4.Text = “x1=” & X1 & “ x2=” & X2
Программу следует проверить на контрольных примерах. Перемещение по окнам сверху вниз — клавишей Tab. . Перемещение по окнам снизу вверх клавишным аккордом — Shift +Tab. Программа будет работать правильно для корректных данных, иначе будет появляться сообщение об ошибке.
🎥 Видео
Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Решение квадратных уравнений вида ax^2 + bx + c = 0. Формула корней квадратного уравненияСкачать

Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

решаем квадратные уравнения в ExcelСкачать

Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

решение (поиск корней) квадратных уравнений c++Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать