Использование свойств и графиков функций при решении уравнений и неравенств метод интервалов

Метод интервалов принято считать универсальным для решения неравенств. Иногда этот метод также называют методом промежутков. Применим он как для решения рациональных неравенств с одной переменной, так и для неравенств других видов. В нашем материале мы постарались уделить внимание всем аспектам вопроса.

Что ждет вас в данном разделе? Мы разберем метод промежутков и рассмотрим алгоритмы решения неравенств с его помощью. Затронем теоретические аспекты, на которых основано применение метода.

Особое внимание мы уделяем нюансам темы, которые обычно не затрагиваются в рамках школьной программы. Например, рассмотрим правила расстановки знаков на интервалах и сам метод интервалов в общем виде без его привязки к рациональным неравенствам.

Алгоритм

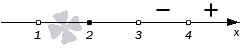
Кто помнит, как происходит знакомство с методом промежутков в школьном курсе алгебры? Обычно все начинается с решения неравенств вида f ( x ) 0 (знак неравенства может быть использован любой другой, например, ≤ , > или ≥ ). Здесь f ( x ) может быть многочленом или отношением многочленов. Многочлен, в свою очередь, может быть представлен как:

• произведение линейных двучленов с коэффициентом 1 при переменной х ;
• произведение квадратных трехчленов со старшим коэффициентом 1 и с отрицательным дискриминантом их корней.

Приведем несколько примеров таких неравенств:

( x + 3 ) · ( x 2 − x + 1 ) · ( x + 2 ) 3 ≥ 0 ,

( x — 2 ) · ( x + 5 ) x + 3 > 0 ,

( x − 5 ) · ( x + 5 ) ≤ 0 ,

( x 2 + 2 · x + 7 ) · ( x — 1 ) 2 ( x 2 — 7 ) 5 · ( x — 1 ) · ( x — 3 ) 7 ≤ 0 .

Запишем алгоритм решения неравенств такого вида, как мы привели в примерах, методом промежутков:

• находим нули числителя и знаменателя, для этого числитель и знаменатель выражения в левой части неравенства приравниваем к нулю и решаем полученные уравнения;
• определяем точки, которые соответствуют найденным нулям и отмечаем их черточками на оси координат;
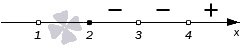
• определяем знаки выражения f ( x ) из левой части решаемого неравенства на каждом промежутке и проставляем их на графике;
• наносим штриховку над нужными участками графика, руководствуясь следующим правилом: в случае, если неравенство имеет знаки или ≤ изображается, штрихуются «минусовые» промежутки, если же мы работаем с неравенством, имеющим знаки > или ≥ , то выделяем штриховкой участки, отмеченные знаком « + ».

Четреж, с которым мы будем работать, может иметь схематический вид. Излишние подробности могут перегружать рисунок и затруднять решение. Нас будет мало интересовать маштаб. Достаточно будет придерживаться правильного расположения точек по мере роста значений их координат.

При работе со строгими неравенствами мы будем использовать обозначение точки в виде круга с незакрашенным (пустым) центром. В случае нестрогих неравенств точки, которые соответствуют нулям знаменателя, мы будем изображать пустыми, а все остальные обычными черными.

Отмеченные точки разбивают координатную прямую на несколько числовых промежутков. Это позволяет нам получить геометрическое представление числового множества, которое фактически является решением данного неравенства.

Научные основы метода промежутков

Основан подход, положенный в основу метода промежутков, основан на следующем свойстве непрерывной функции: функция сохраняет постоянный знак на интервале ( a , b ) , на котором эта функция непрерывна и не обращается в нуль. Это же свойство характерно для числовых лучей ( − ∞ , a ) и ( a , + ∞ ) .

Приведенное свойство функции подтверждается теоремой Больцано-Коши, которая приведена во многих пособиях для подготовки к вступительным испытаниям.

Обосновать постоянство знака на промежутках также можно на основе свойств числовых неравенств. Например, возьмем неравенство x — 5 x + 1 > 0 . Если мы найдем нули числителя и знаменателя и нанесем их на числовую прямую, то получим ряд промежутков: ( − ∞ , − 1 ) , ( − 1 , 5 ) и ( 5 , + ∞ ) .

Возьмем любой из промежутков и покажем на нем, что на всем промежутке выражение из левой части неравенства будет иметь постоянный знак. Пусть это будет промежуток ( − ∞ , − 1 ) . Возьмем любое число t из этого промежутка. Оно будет удовлетворять условиям t − 1 , и так как − 1 5 , то по свойству транзитивности, оно же будет удовлетворять и неравенству t 5 .

Используя оба полученных неравенства и свойство числовых неравенств, мы можем предположить, что t + 1 0 и t − 5 0 . Это значит, что t + 1 и t − 5 – это отрицательные числа независимо от значения t на промежутке ( − ∞ , − 1 ) .

Используя правило деления отрицательных чисел, мы можем утверждать, что значение выражения t — 5 t + 1 будет положительным. Это значит, что значение выражения x — 5 x + 1 будет положительным при любом значении x из промежутка ( − ∞ , − 1 ) . Все это позволяет нам утверждать, что на промежутке, взятом для примера, выражение имеет постоянный знак. В нашем случае это знак « + ».

Нахождение нулей числителя и знаменателя

Алгоритм нахождения нулей прост: приравниваем выражения из числителя и знаменателя к нулю и решаем полученные уравнения. При возникновении затруднений можно обратиться к теме «Решение уравнений методом разложения на множители». В этом разделе мы ограничимся лишь рассмотрением примера.

Рассмотрим дробь x · ( x — 0 , 6 ) x 7 · ( x 2 + 2 · x + 7 ) 2 · ( x + 5 ) 3 . Для того, чтобы найти нули числителя и знаменателя, приравняем их к нулю для того, чтобы получить и решить уравнения: x · ( x − 0 , 6 ) = 0 и x 7 · ( x 2 + 2 · x + 7 ) 2 · ( x + 5 ) 3 = 0 .

В первом случае мы можем перейти к совокупности двух уравнений x = 0 и x − 0 , 6 = 0 , что дает нам два корня 0 и 0 , 6 . Это нули числителя.

Второе уравнение равносильно совокупности трех уравнений x 7 = 0 , ( x 2 + 2 · x + 7 ) 2 = 0 , ( x + 5 ) 3 = 0 . Проводим ряд преобразований и получаем x = 0 , x 2 + 2 · x + 7 = 0 , x + 5 = 0 . Корень первого уравнения 0 , у второго уравнения корней нет, так как оно имеет отрицательный дискриминант, корень третьего уравнения — 5 . Это нули знаменателя.

0 в данном случае является одновременно и нулем числителя, и нулем знаменателя.

В общем случае, когда в левой части неравенства дробь, которая не обязательно является рациональной, числитель и знаменатель точно также приравниваются к нулю для получения уравнений. Решение уравнений позволяет найти нули числителя и знаменателя.

Определение знаков на интервалах

Определить знак интервала просто. Для этого можно найти значение выражения из левой части неравенства для любой произвольно выбранной точки из данного интервала. Полученный знак значения выражения в произвольно выбранной точке промежутка будет совпадать со знаком всего промежутка.

Рассмотрим это утверждение на примере.

Возьмем неравенство x 2 — x + 4 x + 3 ≥ 0 . Нулей числителя выражение, расположенное в левой части неравенства, нулей не имеет. Нулем знаменателя будет число — 3 . Получаем два промежутка на числовой прямой ( − ∞ , − 3 ) и ( − 3 , + ∞ ) .

Для того, чтобы определить знаки промежутков, вычислим значение выражения x 2 — x + 4 x + 3 для точек, взятых произвольно на каждом из промежутков.

Из первого промежутка ( − ∞ , − 3 ) возьмем − 4 . При x = − 4 имеем ( — 4 ) 2 — ( — 4 ) + 4 ( — 4 ) + 3 = — 24 . Мы получили отрицательное значение, значит весь интервал будет со знаком « — ».

Для промежутка ( − 3 , + ∞ ) проведем вычисления с точкой, имеющей нулевую координату. При x = 0 имеем 0 2 — 0 + 4 0 + 3 = 4 3 . Получили положительное значение, что значит, что весь промежуток будет иметь знак « + ».

Можно использовать еще один способ определения знаков. Для этого мы можем найти знак на одном из интервалов и сохранить его или изменить при переходе через нуль. Для того, чтобы все сделать правильно, необходимо следовать правилу: при переходе через нуль знаменателя, но не числителя, или числителя, но не знаменателя мы можем поменять знак на противоположный, если степень выражения, дающего этот нуль, нечетная, и не можем поменять знак, если степень четная. Если мы получили точку, которая является одновременно нулем числителя и знаменателя, то поменять знак на противоположный можно только в том случае, если сумма степеней выражений, дающих этот нуль, нечетная.

Если вспомнить неравенство, которое мы рассмотрели в начале первого пункта этого материала, то на крайнем правом промежутке мы можем поставить знак « + ».

Теперь обратимся к примерам.

Возьмем неравенство ( x — 2 ) · ( x — 3 ) 3 · ( x — 4 ) 2 ( x — 1 ) 4 · ( x — 3 ) 5 · ( x — 4 ) ≥ 0 и решим его методом интервалов. Для этого нам необходимо найти нули числителя и знаменателя и отметить их на координатной прямой. Нулями числителя будут точки 2 , 3 , 4 , знаменателя точки 1 , 3 , 4 . Отметим их на оси координат черточками.

Нули знаменателя отметим пустыми точками.

Так как мы имеем дело с нестрогим неравенством, то оставшиеся черточки заменяем обычными точками.

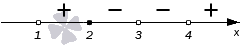
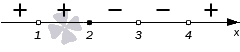
Теперь расставим точки на промежутках. Крайний правый промежуток ( 4 , + ∞ ) будет знак + .

Продвигаясь справа налево будем проставлять знаки остальных промежутков. Переходим через точку с координатой 4 . Это одновременно нуль числителя и знаменателя. В сумме, эти нули дают выражения ( x − 4 ) 2 и x − 4 . Сложим их степени 2 + 1 = 3 и получим нечетное число. Это значит, что знак при переходе в данном случае меняется на противоположный. На интервале ( 3 , 4 ) будет знак минус.

Переходим к интервалу ( 2 , 3 ) через точку с координатой 3 . Это тоже нуль и числителя, и знаменателя. Мы его получили благодаря двум выражениям ( x − 3 ) 3 и ( x − 3 ) 5 , сумма степеней которых равна 3 + 5 = 8 . Получение четного числа позволяет нам оставить знак интервала неизменным.

Точка с координатой 2 – это нуль числителя. Степень выражения х — 2 равна 1 (нечетная). Это значит, что при переходе через эту точку знак необходимо изменить на противоположный.

У нас остался последний интервал ( − ∞ , 1 ) . Точка с координатой 1 – это нуль знаменателя. Он был получен из выражения ( x − 1 ) 4 , с четной степенью 4 . Следовательно, знак остается прежним. Итоговый рисунок будет иметь вот такой вид:

Применение метода интервалов особенно эффективно в случаях, когда вычисление значения выражения связано с большим объемом работы. Примером может стать необходимость вычисления значения выражения

x + 3 — 3 4 3 · x 2 + 6 · x + 11 2 · x + 2 — 3 4 ( x — 1 ) 2 · x — 2 3 5 · ( x — 12 )

в любой точке интервала 3 — 3 4 , 3 — 2 4 .

Будем считать, что с правилами определения знаков для промежутков мы разобрались. Идем дальше.

Использование свойств функций при решении уравнений и неравенств

Презентация к уроку

Загрузить презентацию (352 кБ)

Правильному применению методов можно научиться только применяя их на разнообразных примерах.
И.Г. Цейтен

Цели урока:

• дидактические: продолжить формирование умений применять различные способы решения неравенств; совершенствовать навыки решения неравенств различными методами;
• развивающие: развивать познавательный интерес у учащихся, логическое мышление, интеллектуальные способности; формировать математическую речь;
• воспитательные: воспитывать у учащихся такие качества личности как познавательная активность, самостоятельность, упорство в достижении цели, потребность в приобретении и углублении знаний, вырабатывать умение слушать и вести диалог, формировать эстетические навыки при оформлении записей в тетради.

Тип урока: урок систематизации и обобщения изученного материала

Структура урока:

1. Организационный этап.
2. Этап подготовки учащихся к активному и сознательному усвоению материала.
3. Этап обобщения и систематизации изученного.
4. Этап подведения итогов.
5. Этап информации учащихся о домашнем задании.

Оборудование: компьютер, мультимедийный проектор, экран, презентация “Использование свойств функций при решении уравнений и неравенств”, доска, мел, раздаточный материал для работы на уроке и домашним заданием.

Деятельность учителя	Деятельность учащихся
Организационный этап.
Здравствуйте, рада вас всех видеть!		Ответы учащихся: Здравствуйте!
Этап подготовки учащихся к активному и сознательному усвоению материала.
Эпиграфом к уроку я выбрала слова датского математика и историка математики, жившего с 1839 по 1920 года, Иеромонима Георга Цейтена: “Правильному применению методов можно научиться только применяя их на разнообразных примерах”.

При решении практически любой математической задачи приходится производить преобразование числовых, алгебраических или функциональных выражений. Но бывают случаи, когда стандартные преобразования не позволяют получить ответ. Тогда используют нестандартные методы, суть которых – реализовать “иной взгляд” на задачу, что существенно упрощает решение некоторых задач. Таким образом, тема сегодняшнего урока…

Но для начала — вопросы, ответы на которые вы должны были повторить дома.

“Использование свойств функций при решении уравнений и неравенств”.Слайд 3

Что называется функцией?Пусть каждому числу x из множества чисел X в силу некоторого закона f поставлено в соответствие единственное число y. Тогда говорят, что задана функция , определенная на множестве X; при этом x называют независимой переменной или аргументом, а переменную y – зависимой переменной.Какие свойства функций вам известны?Область определения функции.

Область значений (область изменения).Ограниченность функции.

Возрастание, убывание функции.

Четность, нечетность функции.

Периодичность функции.Что называется областью определения функции?Из определения функции следует, что функция задается вместе с областью определения X. Чаще всего функцию задают с помощью какой-либо формулы. При этом, если не дано дополнительных ограничений, то областью определения функции, заданной формулой, считают множество всех значений переменной, при которых эта формула имеет смысл.Что называется областью значения функции?Область значений (область изменения) – множество всех значений функции .

Функцию называют ограниченной снизу (сверху), если существует такое число M, что для любого x из области определения верно неравенство , (). Функция называется ограниченной, если она ограничена и сверху и снизу.Что понимается под монотонностью функции?

Все определения можно ещё раз увидеть в Приложении 1, которое лежит у вас на партах.Функция возрастает (убывает), если большему значению аргумента соответствует большее (меньшее) значение функции. Общее название этих двух понятий – монотонность.3. Этап обобщения и систематизации изученного.Судя по тем вопросам, которые я задала вам в начале урока, как вы думаете, какие свойства легли в основу методов, которые мы с вами сегодня будем разбирать? Слайд 3Область определения, ограниченность функции, её монотонность.Для более удобного рассмотрения нестандартных методов я составила для вас таблицу. Она у каждого из вас. С её помощью на сегодняшнем уроке мы разберём три метода. Учитель разбирает методы по таблице: пояснения теоретической части, разбор 1-2 примеров (какого — по желанию учащихся). Приложение 2.

Слайды 4 – 7.Ученики слушают объяснения учителя, делая пометки в таблице.А сейчас вы будете работать в группах. Каждая группа выберет себе задание. Затем представитель от группы представит решение.

1 группа. Решить уравнение .

2 группа. Решить неравенство .

3 группа. Решить неравенство .Учащиеся работают в группах.Защита решений. Слайд 8От каждой группы выступает 1 человек с защитой своего решения (решение на доске кратко записать, пояснения по ходу решения).

1группа. .

Решение: при решении используем ограниченность функций и квадратичной функций:

1. для любого х из R.

2. .

Таким образом мы видим, что области значений левой и правой части этого уравнения не имеют “точек соприкосновения”. Значит уравнение не имеет решений.

Ответ: решений нет.

2 группа. .

Решение: при решении используем анализ ОДЗ неравенства.

ОДЗ: .

х=1 не является решением. Тогда при получим, что , а . Значит решением данного неравенства являются все числа из промежутка.

Ответ:

3 группа. .

Решение: при решении используем монотонность функций, входящих в неравенство.

Рассмотрим функции . Все они непрерывны и строго возрастают на R. значит и сумма этих функций тоже будет возрастающей функцией. Легко увидеть, что . А в силу её непрерывности и строгой монотонности получим, что при имеем, а при имеем. Значит решениями являются все .

Ответ: 4.Этап подведения итогов.Ребята, подведём итоги сегодняшнего занятия. Слайд 9.

1. Какие неравенства мы сегодня рассматривали?
2. Какими алгоритмами мы пользовались?
3. Какие затруднения у вас вызвали эти методы? В чём они выражались?
4. А чем понравились эти методы? Как вы думаете в чём их плюсы, а в чём — минусы?

Учащиеся отвечают, используя записи; рассказывают о своих затруднениях, если они были; высказывают личное мнение о методе.5. Этап информации учащихся о домашнем задании.На следующем занятии мы продолжим решать уравнения и неравенства, с использованием уже других свойств функций. А по теме сегодняшнего урока вам необходимо к следующему уроку выполнить следующее задание (карточки): Слайд 10

2. Творческое задание.

Подумайте, какие “внешние” признаки могут содержать уравнения или неравенства, которые бы указывали на применение рассмотренных сегодня методов.

Всем спасибо! Слайд 11

Литература.

1. П. В. Чулков Материалы курса “Уравнения и неравенства в школьном курсе математики” – М.:”Педагогический университет “Первое сентября”, 2010.
2. Олехник С.Н., Потапов М.К., Пасиченко П.И. Уравнения и неравенства. Нестандартные методы решения. Учимся решать задачи. 10-11 классы: Учебно-методическое пособие. – М.: Дрофа. 2002 г.
3. Математика. Тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов / сост. Г.И. Ковалева, Т.И. Бузулина, О.Л. Безрукова, Ю.А. Розка – Волгоград: Учитель, 2005.
4. Математика. Подготовка к ЕГЭ. Нестандартные методы решения уравнений и неравенств: учебно-методическое пособие/ Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова. – Ростов – на – Дону: Легион, 2013.
5. В. К. Егерев, В. В. Зайцев, Б. А. Кордемский и др.; под ред. М. И. Сканави. Сборник задач по математике (с решениями) – М.: ООО”Издательский дом “ОНИКС 21 век”: ООО “Издательство “Мир и Образование”, 2005.

Замечание. По данной теме проводится ещё два урока: 2 урок – использование четности, периодичности, решение задач, 3 урок – самостоятельная работа.

Использование свойств и графиков функций при решении уравнений и неравенств метод интервалов

«Правильному применению методов можно научиться,

только применяя их на разнообразных примерах».

Решение неравенств повышенной сложности, содержащих модули, иррациональные, логарифмические, показательные функцииили их комбинацию, стандартными школьными методами часто оказывается весьма сложным и громоздким, что вызывает у нас, школьников, определенные трудности.

Одним из эффективных и доступных методов решения таких неравенств и их систем являются методы, опирающиеся на такие свойства функций, как область определения и область значений, неотрицательность, монотонность и ограниченность, экстремумы функций и метод «мини-максов». Суть данных методов заключается на замене иррациональных и трансцендентных неравенств на равносильные им рациональные алгебраические неравенства, решение которых легко осуществляется. Применение этих методов позволяет во многих случаях значительно уменьшить трудоемкость задачи, избежать длинных выкладок и ненужных ошибок.

Мною было проведено анкетирование среди учащихся 9-11 классов:

Знаете ли вы методы решения неравенств, опирающиеся на свойства функций?

Какие вы используете чаще всего?

По результатам анкетирования были получены следующие результаты:

Проанализировав полученные результаты, я пришел к выводу, что большинство учащихся недостаточно осведомлены о данных методах решения неравенств.

Таким образом, возникает необходимость в изучении методов решения неравенств, опирающихся на свойства функций, что определяет актуальность данной работы.

Цель: научиться использовать методы решения неравенств, опирающиеся на свойства функций.

Рассмотреть методы решения неравенств, опирающиеся на свойства функций, такие как область определения, ограниченность, неотрицательность, монотонность функций и метод мини-максов;

Привести примеры решения неравенств с помощью методов, опирающихся на свойства функций;

Составить тренажер по использованию свойств функций при решении неравенств.

Объект исследования: методы решения неравенств.

Предмет исследования: методы решения неравенств, опирающиеся на свойства функций.

Гипотеза исследования: использование свойств функций при решении неравенств дает более рациональное его решение и позволяет повысить эффективность и качество.

Методы исследования: анализ, сравнение, обобщение, конструирование, моделирование, изучение литературных источников и Интернет-источников.

Практическая значимость исследования: изучение методов решения неравенств, опирающихся на свойства функций, необходимы для получения хорошего результата на ЕГЭ, при поступлении в ВУЗы и различных жизненных ситуациях.

Глава 1. Понятие функции

Понятие «функция» является одним из основных понятий в математике. Термин «функция» (в некотором более узком смысле) был впервые использован Лейбницем (1692 год). В свою очередь, Иоганн Бернулли в письме к тому же Лейбницу употребил этот термин в смысле, более близком к современному.

Первоначально понятие функции было неотличимо от понятия аналитического представления. Впоследствии появилось определение функции, данное Эйлером (1751 год), затем — у Лакруа (1806 год), — уже практически в современном виде. Наконец, общее определение функции (в современной форме, но для числовых функций) было дано Лобачевским (1834 год) и Дирихле (1837 год).

К концу XIX века понятие функции переросло рамки числовых систем. Сначала понятие функции было распространено на векторные функции, вскоре Фреге ввёл логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение.

Зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у, называется функцией (определение, которое нам знакомо из курса алгебры).

При этом x называют независимой переменной или аргументом, а переменную y – зависимой переменной или функцией.

Если зависимость переменной у от переменной х является функцией, то коротко это записывают y = f ( x ).

Область определения функции — все значения независимой переменной.

Область значений функции – все значения, которые принимает зависимая переменная.

Глава 2. Использование свойств функции

2.1. Использование области определения функций

Предварительный анализ области определения функций, входящих в неравенство (ОДЗ неизвестной), иногда позволяет получить решение без преобразований.

Если множество M, на котором определены обе части неравенства, окажется пустым множеством, то в этом случае неравенство решений не имеет.

Использование областей существования наиболее результативен при решении уравнений и неравенств, в состав которых входят функции: y = arcsinx , y = arccosx , y = log _a x , y =  x .

Пример 1. Решите неравенство

Проверим полученные значения на исходное неравенство.

Использование ограниченности функций

Использование неотрицательности функций

Пусть левая часть неравенства F ( x )0 есть сумма функций F ( x )= f ( x )+ g ( x ).Установили, что каждая из этих функций неотрицательна на своей области определения. Тогда неравенство F ( x ) ≤ 0 равносильно системе уравнений

При тех же условиях неравенство F ( x ) ≥ 0 сводится к нахождению области определения функции F ( x ):

Пример 2. Решите неравенство
Решение. (1)  f ₁( x )+ f ₂( x )≥0, (2)

где 1) ООН: (2 x – 1) 4 – (2 x – 1) 2 ≥0  (2 x – 1) 2 ((2 x – 1) 2 –1) ≥0 

(2 x – 1) 2 (2 x – 1–1) (2 x – 1+1) ≥0  (2 x – 1) 2 ( x – 1) x ≥0

2)Так как f ₁( x )≥0, f ₂( x )≥0 на ООН, то (2)  x  ООН  x  (-  ;0  0,5  1;+  ).

Пример 3. Решите неравенство

Решение. (1)  f ₁( x )+ f ₂( x ) ≤ 0, (2)

Пример 4. Решите систему неравенств

Решим неравенство (2).

Метод мини-максов (метод оценки)

Иногда неравенство f ( x )  g ( x ) устроено так, что на всей ОДЗ неизвестной х имеет место неравенства f ( x )≥ A , g ( x )≤ A .

а) решение неравенства f ( x ) ≤ g ( x ) сводится к нахождению тех значенийх, для которых f ( x )= A и g ( x )= A , т.е.

б) решение неравенства f ( x )≥ g ( x ) сводится к нахождению ОДЗ неизвестной переменной.

Как понять, что нужно решать именно предложенным методом? Для этого нужно знать основной признак подобных задач: имеется смешанное неравенство, то есть в задании присутствуют разнородные функции, например: линейная и логарифмическая, тригонометрическая и квадратичная.

Пример 5. Решите неравенство

Решение: Преобразуем данное неравенство: . Т.к. , то . Мы получили неравенство вида

Рассмотрим . Преобразуем подлогарифмическое выражение: . Получаем, что подлогарифмическое выражение

Т. к. возрастает при , то

Рассмотрим . Мы знаем, что возрастает. Т. к. то Получаем, что M =1. Следовательно, неравенство равносильно системе:

Решив второе уравнение системы, получаем . Проверим первое уравнение, подставив значение x .

Получаем верное равенство Значит, является решением неравенства .

Использование монотонности функций

Принцип монотонности для неравенств

Пусть функция y = f ( x ) определена и строго монотонна на промежутке М.

Если функция y = f ( x ) возрастает на промежутке М, то

Если функция y = f ( x ) убывает на промежутке М, то

Использование монотонности функций при решении уравнений и неравенств используется чаще всего. Решение уравнений и неравенств с применением монотонности функций основывается на следующих утверждениях:

Теорема о корне

Если в уравнении f ( x )= C = const функция y = f (x) непрерывна и строго монотонна на множестве М, то уравнение имеет на М не более одного корня.

Если в уравнении f ( x )= g ( x ) функция y = f (x) непрерывна и строго возрастает, а функция y = g ( x ) непрерывна и строго убывает на множестве М, то уравнение имеет на М не более одного корня.

Пример 6. Решите неравенство

ООН: 2х-3 ≥ 0  х≥1,5.

Функция возрастает при х≥1,5, как сумма двух возрастающих функций.

Так как , то по теореме о корне х=2 – единственный корень уравнений f ( x )=3.

Пример 7. Решите неравенство 4(1+ log ₃( x 2 +3 x -7))≥18-3 x — x 2 (1)

Решение. (1)  4 log ₃( x 2 +3 x -7)+( x 2 +3 x -14)≥0 (2)

t=x 2 +3 x– 7 , x 2 +3x –14=t – 7.

где f(t) =4 log ₃ t+t – 7.

Функция y = f ( t ) возрастает при t > 0, как сумма двух возрастающих функций.

Так как f (3)=4+3 – 7=0, то по теореме о корне t =3 единственный корень уравнения f ( t )=0.

Пример 8. Решите неравенство

Применим МЗМ. Заменим функции f ₁( x ) и f ₂( x ) на функции равного знака.

Функция y = f ₁( t )= arcos ( t ) убывает на t  -1;1 

Функция y = f ₂(х) убывает на хх₁;3. Так как f ₂(4)=0, то по теореме о корне х=4 единственный корень уравнения f ₂(х)=0 

Глава 3. Тренажер «Методы решения неравенств, используя свойства функций»

Мне захотелось составить тренажер по усвоению методов решения неравенств, используя свойства функций. Традиционно ученику предлагается решить неравенство, а я предлагаю ознакомиться с решением неравенства и определить, какой метод используется при решении данного неравенства. Этот тренажер составлен с помощью конструктора интерактивных заданий LearningApps. Учащиеся могут проверить и закрепить свои знания по данным методам, что способствует формированию их познавательного интереса к математике:

https :// learningapps . org / watch ? v = pvh 1 b 1 qak 20

В ходе выполнения исследования были достигнуты поставленная цель и задачи. Гипотеза подтвердилась. Использование свойств функций при решении неравенств: таких как область определения и область значений, неотрицательность, монотонность и ограниченность, экстремумы функций и метод «мини-максов, позволяет избежать огромных преобразований. Применение этих методов дает более рациональное решение неравенства и позволяет повысить эффективность и качество.

Для каждого из указанных типов неравенств приведены методические указания и алгоритмы (схемы), а также подробные и обоснованные решения неравенств разных типов и разного уровня сложности, иллюстрирующие оригинальность и эффективность приведенных методов, позволяющих решать задачи компактно, быстро и просто. Составлен тренажер по усвоению методов решения неравенств, используя свойства функций.

Выбор способа решения должен оставаться за нами, учащимися. Каждый ученик должен уметь верно, и главное рационально решать неравенства, что в дальнейшем может ему пригодиться при поступлении в ВУЗы и различных жизненных ситуациях. Они могут воспользоваться собранной информацией для изучения и закрепления методов решения неравенств.

Я считаю, что проделанная работа будет интересна всем, кто хочет научиться рационально решать неравенства и хорошо подготовиться к выпускным экзаменам.

Хочется отметить и то, что излагаемая тема в данном исследовании еще недостаточно изучена, поэтому она таит в себе много скрытого и неизвестного, что дает прекрасную возможность для дальнейшей работы над ней.

Алгебра и начала анализа: Учебник для 10-11 кл. / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын, Б. М. Ивлев, С. И. Шварцбурд; Под ред. А. Н. Колмогорова. – 12-изд. – М.: Просвещение, АО «Московские учебники», 2002. – 384с.

ЕГЭ 2017. Математика. 10 вариантов экзаменационных работ. Профильный уровень. Под ред. И. В. Ященко/ М.: «Экзамен», 2017.

Куланин Е. Д., Норин В. П. 3000 конкурсных задач по математике. М.:Айрис-пресс, 2003.

Коропец З.Л., Коропец А.А., Алексеева Т.А. Нестандартные методы решения неравенств и их систем. Орел: ОрелГТУ, 2012.

Математика: Учебно-методический журнал – М.: Первое сентября, 2009.

Сергеев И.Н., Панферов В.С. ЕГЭ 2011. Математика. Задача С3. Уравнения и неравенства. / Под ред. А.Л. Семенова, И.В. Ященко. – М.:МЦНМО, 2011.

💥 Видео