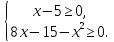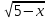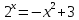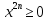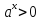Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться , такую группу уравнений мы называем системой.
Объединяем уравнения в систему с помощью фигурной скобки:
- Графический метод
- Пример 1
- Пример 2
- Пример 3
- Пример 4
- Пример 5
- Видео YouTube
- Применение свойств функций для решения уравнений
- Просмотр содержимого документа «Применение свойств функций для решения уравнений»
- Конспект урока алгебры в 9 классе. Графическое решение систем уравнений. план-конспект занятия по алгебре (9 класс) на тему
- Скачать:
- Предварительный просмотр:
- 🎦 Видео
Графический метод
Недаром ответ записывается так же, как координаты какой-нибудь точки.
Ведь если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.
Например, построим графики уравнений из предыдущего примера.
Пример 1
Для этого сперва выразим y y y в каждом уравнении, чтобы получить функцию (ведь мы привыкли строить функции относительно x x x ):
Для того чтобы графически решить систему уравнений с двумя переменными нужно:
1) построить графики уравнений в одной системе координат;
2) найти координаты точек пересечения этих графиков (координаты точек пересечения графиков и есть решения системы);
Разберем это задание на примере.
Решить графически систему линейных уравнений.
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Пример 2
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может:
а) иметь единственное решение;
б) не иметь решений;
в) иметь бесконечное множество решений.
2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Пример 3
Графическое решение системы
Пример 4
Решить графическим способом систему уравнений.

Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
Пример 5

Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В(-2; 5).
ОБЯЗАТЕЛЬНО: Познакомимся с видео, где нам объяснят как решаются системы линейных уравнений графическим способом. РАССКАЖУТ, КАК РЕШАТЬ СИСТЕМЫ ГРАФИЧЕСКИ.
Видео YouTube
Видео:Использование свойств функций при решении уравнений и неравенствСкачать

Применение свойств функций для решения уравнений
В работе рассматриваются сособы решения уравнений с использованием свойств и характеристик функций: монотонности, ограниченности, области определенийи области значений функции.
Просмотр содержимого документа
«Применение свойств функций для решения уравнений»
II. Применение свойств функций для решения уравнений
Использование ОДЗ для решения уравнений .………….. 2стр
Монотонность функции и наличие корней уравнении…. 3стр
Используемая литература………………………………………. 10 стр
Найти и освоить приемы решения уравнений способами, позволяющими значительно сократить время нахождения корней уравнений.
В ходе сбора и изучения информации по данной теме, были найдены и изучены рациональные приемы решения уравнений с применением свойств монотонности, ограниченности функций, а также области определения и значений функций, позволяющие эффективно (практически устно) решать некоторые виды уравнений, рассмотренных в качестве примеров в нашей работе.
В наших школьных учебниках алгебры в основном изучаются такие методы и приемы решения уравнений как возведение в степень, замена переменной, применение тождественных преобразований, Но использование этих способов при решении некоторых видов уравнений приводит к довольно долгим и сложным преобразованиям, особенно если уравнения в левой и правой части которой находятся функции, имеющие различную природу.
В ходе наших поисков мы познакомились с одним из эффективных способов решения уравнений вида f(x)=g(x), который и демонстрируем в нашей работе. Это способ решения уравнений с использованием свойств функций.
Начнем с уравнений, которые можно решить, используя область определения функции или область допустимых значений переменной. Напомним, что множество значений переменной, при которых обе части данного уравнения (или неравенства) имеют смысл называют областью допустимых значений уравнения или неравенства. Рассмотрим такие уравнения, которые можно решить просто найдя ОДЗ.
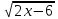
Пусть f(x) = 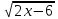
Значит правая часть уравнения должна быть неотрицательной, т.е. должно выполнятся условие 3−x ≥ 0, тогда x ≤ 3. Определяется системой двух неравенств: x≥3 и x ≤ 3. Получаем, что ОДЗ уравнения: х=3.Легко видеть, что 3 будет корнем исходного уравнения.
Приведем еще один пример уравнения:
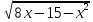
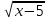
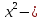
Решение: Найдем ОДЗ, решив систему неравенств
Решая неравенства этой системы получим 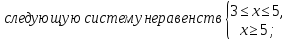
Монотонность функции и наличие корней уравнения.
Рассмотрим как применяются такое свойство функции как монотонность. Для успешного решения уравнения этим способом необходимо знать следующие утверждения: 1) если функция f (х) на некотором промежутке возрастает, а функция g(х) убывает на этом же промежутке, то уравнение f(х) = g(х) имеет на этом промежутке не более одного корня; 2) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)). Применение свойства продемонстрируем на следующих примерах:
1) x 1991 +1 =
1) В левой части этого уравнения стоит возрастающая функция на на R
в правой – убывающая на (-∞;5].
Если уравнение и будет иметь корень, то только на промежутке (-∞;5]. Легко заметить, что этот корень 1, и он, согласно теореме, единственный.
2) 5x 19 + 4x 3 +3х=12. Функция, стоящая в левой части уравнения является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.
3) 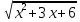
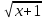
4) 2 x 15 + 3x=5/х. Функция f(x) = 5/х на каждом из промежутков (-∞;0) и (0:∞) убывает, а функция g (х) = 2 x 15 + 3x возрастает на каждом из них, поэтому наше уравнение на каждом из этих промежутков имеет не более одного корня. Убеждаемся, что это числа 1 и -1.
5) 2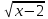
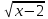
6) найти положительные корни уравнения
Функция 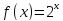
Убывает на промежутке [ 0; ∞). Следовательно, на промежутке [ 0; ∞) уравнение имеет не более одного корня. Подбором находим что х =1.
Функция 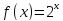
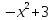
Рассмотрим, как можно применить к решению уравнений такое свойство функции как ограниченность. Метод, с помощью которого решаются уравнения с применением ограниченности функции, получил название метода мажорант. Ну, а само название метода происходит от французского слова majorer — объявлять большим. Мажорантой данной функции f(х) на множестве Р, называется такое число М, что либо f(х) ≤ М для всех х ϵ Р, либо f(х) ≥ М для всех х ϵ Р. Основная идея метода состоит в следующем: Пусть имеется уравнение f(х) = g(х) и существует такое такое число М, что для любого х из области определения f(х) и g(х) имеем f(х) ≤ М и g(х) ≥ М. Тогда уравнение f(х) = g(х) равносильно системе 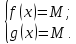
1. 
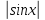
2. -1≤cosx≤1 или 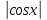
3.
4.

6.

1) Решим уравнение: + =0.
4и 10 степени – это четные числа, значит и при любом значении x. Тогда наше уравнение будет равносильно системе уравненийПервое уравнение имеет единственный корень – это число3, значит, если система и будет иметь решение, то не более одного. Проверкой убеждаемся, что3 является корнем и второго уравнения системы, а следовательно и исходного уравнения.
Заменим левую часть уравнения логарифмом, используя свойство разности логарифмов:
Представим дробь в виде , и используя неравенство Коши оценим подлогарифмическое выражение. Получаем (x + ) ≥ 4, а значит
log2 (x + ) ≥ 2. Таким образом, левая часть уравнения не меньше 2.
Рассмотрим правую часть уравнения. В правой части содержится квадратный трехчлен, поэтому выделив из него квадрат двучлена приходим к выводу, что данное выражение принимает значения не больше 2:
4 x – x 2 – 2 = – x 2 + 4 x – 2 = – ( – 4 x + 4 – 2) = – (x — 2) 2 + 2 = 2 – ( x — 2) 2
Получили, что правая часть уравнения не больше 2, т.к. (x — 2) 2 ≥ 0 при любых х. Значит, равенство левой и правой частей уравнения достигается, если они одновременно равны 2.
Из первого уравнения системы находим корень х = 2. Убеждаемся, что этот корень удовлетворяет и второму уравнению системы. Следовательно, решением исходного уравнения будет х = 2.
3) Решить уравнение:
В левой части уравнения стоит тригонометрическая функция, а в правой – сумма показательных. Формул, позволяющих находить корни в таких случаях, не существует. Оценим каждую из частей уравнения. Очевидно, что левая часть уравнения не больше 2. И так как
Поскольку 0, то причем равенство достигается только при x = 0. В данном случае
Получили, что левая часть уравнения не больше двух, а правая часть – больше или равняется двум. Таким образом, уравнение имеет решение, только если имеет решение система уравнений:
Проверкой убеждаемся, что x=0 – корень уравнения: . Значит число 0 – корень исходного уравнения. Получили ответ: x = 0.
Рассмотрим решение еще одного уравнения:
Рассмотрим две функции
Уравнение имеет решение, если наибольшее значение функции f(х) равно наименьшему значению функции g(х). Таким образом, уравнение имеет решение, только если обе части равны 2. И наше уравнение равносильно системе:
Решим первое уравнение системы:
Подставив данный корень во второе уравнение системы, получим верное равенство. Значит, решением исходного уравнения будут числа вида .
Функция y= (квадратичная функция) имеет наименьшее значение при , равное y(2)=4
Функция у= является возрастающей и, следовательно, принимает наименьшее значение при x=2
Правая часть уравнения, в силу ограниченности функции принимает значения не больше 2, поэтому исходное уравнение равносильно системе:
Так как 2-корень первого уравнения, то убедимся, что число 2-корень второго уравнения. Получаем:
Таким образом, 2-корень исходного уравнения.
Рассмотренные нами примеры могли быть решены и другими методами, но традиционные методы в данных конкретных примерах достаточно трудоемки. В нашей работе мы постарались продемонстрировать применение некоторых нестандартных приемов решения уравнений, основанных на свойствах и характеристиках функций. Планируем продолжить изучение нетрадиционных и эффективных приемов решения уравнений.
Видео:Использование свойств и графиков функций при решении неравенств | МатематикаСкачать

Конспект урока алгебры в 9 классе. Графическое решение систем уравнений.
план-конспект занятия по алгебре (9 класс) на тему
Конспект урока алгебры в 9 классе «Использование графиков функций для решения систем уравнений»
Видео:Урок 13. Функции и их свойства. Построение графиков сложных функций. Вебинар | МатематикаСкачать

Скачать:
| Вложение | Размер |
|---|---|
| konspekt_uroka_algebry_v_9_klasee._graf_reshenie_sistem_uravneniy.docx | 43.71 КБ |
Видео:Функции и их свойства #6Скачать

Предварительный просмотр:
Муниципальное казенное общеобразовательное учреждение
«Центр образования № 14»
Урок по алгебре
«Использование графиков функций для решения систем уравнений»
Провела: учитель математики
Ли Светлана Александровна
ЦЕЛЬ УРОКА: Закрепление знаний учащимися по решению систем уравнений графическим способом , отработка умения решения систем уравнений графическим способом
- привести в систему теоретические знания по теме «Графический способ решения систем уравнений»;
- закрепить навыки построения графиков функций;
- подготовка к ОГЭ.
- воспитание аккуратности, внимательности, рационального использования времени при выполнении заданий.
- воспитание у учащихся дисциплинированности на уроках;
- научить использовать для описания математических ситуаций графический язык;
- применять геометрические представления для решения систем уравнений.
презентация к уроку,
карточки с задачами;
1. Организационный момент — 2 минуты
( ознакомление с темой урока, постановка его цели)
2. Проверка домашнего задания. 3-4 минуты.
3. Просмотр презентации, подготовленной учениками, «Графики функций. Повторение»
4.Работа по карточкам. 5-6 минут.
5.Расположение графиков линейной функции y=kx+b в зависимости от коэффициента «k» и числа «b».5 минут.
6. Презентация «Графический способ решения систем уравнений». 5 минут.
7.Решения задач из учебника.10 минут.
8.Индивидуальные задания по карточкам.10 минут.
9.Подведение итогов урока.5 минут.
1. Ознакомление с темой урока, постановка его цели.
Учитель проверяет готовность класса к уроку, после чего напоминает учащимся, что на этом занятии закрепляется изучение темы «Решение систем уравнений графическим способом».
Учитель сообщает цель урока, ставит перед учащимися задачи урока.
2. Проверка домашнего задания.
Если есть вопросы по выполнению домашнего задания, то задания разбираются на доске.
3. Просмотр презентации, приготовленной учащимися на уроке информатики, на слайдах которой изображены графики изученных ранее функций.
4.Работа по карточкам.
На карточках изображены графики функций, на доске написаны формулы. Учащимся необходимо установить соответствие между графиками на карточках и формулами на доске.
5.Повторение. Расположение графика линейной функции .
Один ученик у доски рассказывает о расположении графика линейной функции на координатной плоскости в зависимости от «k» и «b». Схематически изображает рассматриваемые случаи.
6.Презентация «Графический способ решения систем уравнений».
7.Решения задачи из учебника.
Страница 36, №5.19 (в).
8.Индивидуальные задания по карточкам (для 3 групп учащихся).
Карточка №1 (для слабых учащихся)
Это линейные уравнения, графиком каждого из них является прямая. График первого уравнения проходит через точки (0; 1) и (-1; 0). График второго уравнения проходит через точки (0; -1) и (-1; 0). Прямые пересекаются в точке (-1; 0), это и есть решение системы уравнений (Рис.1)
Решением системы является пара чисел Подставив эту пару чисел в каждое уравнение, получим верное равенство.
Мы получили единственное решение линейной системы.
График первого уравнения – прямая, график второго уравнения – окружность. Построим первый график по точкам (Рис. 2).
Центр окружности в точке О(0; 0), радиус равен 1.
Графики пересекаются в т. А(0; 1) и т. В(-1; 0).
Ответ:
Решить систему графически
Решение: Построим график первого уравнения – это окружность с центром в т.О(0; 0) и радиусом 2. График второго уравнения – парабола. Она сдвинута относительно начала координат на 2 вверх, т.е. ее вершина – точка (0; 2) (Рис. 3).
Графики имеют одну общую точку – т. А(0; 2). Она и является решением системы. Подставим пару чисел в уравнение, чтобы проверить правильность.
9.Подведение итогов урока.
Учащиеся высказываются о своих впечатлениях от урока. Выставление оценок.
10. Домашнее задание.
Вариант теста ОГЭ прошлых лет (1-8 задание), № 5.21 (а,б)
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 17-е изд. – М.: Мнемозина, 2014.-232 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 17-е изд. — М.: Мнемозина, 2014.-223 с.: ил.
🎦 Видео
8 класс, 46 урок, Применение неравенств к исследованию свойств функцийСкачать

Алгебра 9 класс (Урок№3 - Свойства функций)Скачать

Свойства функций. Алгебра, 9 классСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Математика без Ху!ни. Непрерывность функции, точки разрыва.Скачать

Применение свойств функций к решению уравнений - Distance-teacher.ruСкачать
Функция. 10 класс.Скачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Функция y=√x, ее свойства и график. 8 класс.Скачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

ГРАФИК ФУНКЦИЙ — Сдвиги Графика Функции, Как строить Графики Функции // Алгебра 8 классСкачать

Преобразование графиков функций. Сжатие и растяжение. 10 класс.Скачать

10 класс, 16 урок, Функции y=sinx, y=cosx, их свойства и графикиСкачать

ФУНКЦИЯ y = √¯x ( корень из х ) МАТЕМАТИКАСкачать
Исследование функции. 10 класс.Скачать

Алгебра 10 класс (Урок№2 - Функции и графики. Линейная и квадратичная функции.)Скачать