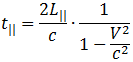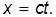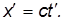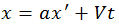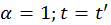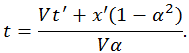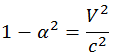Инвариантность уравнений относительно преобразований лоренца (4 видео)

Фантазии о физической причине лоренцева сокращения, объясняющей инвариантность скорости света и пр

Всем известно об инвариантности скорости света в любой инерциальной системе отсчёта, но наука пока не может объяснить физику, т.е. природу механизма этого феномена.

Математическая же модель явления постулирует, что все процессы протекают в 4-х мерном пространстве-времени, в котором феномены СТО следуют из сохранения интервала событий при преобразованиях вращения системы координат. Вряд ли можно отрицать, что реальность как бы натягивают на математические конструкции. Причём то, что в оных почти сплошь важную роль играют мнимые числа, в реальности непредставимые, нисколько не умаляет успехов науки. Ещё Э.Мах говорил, что объяснения излишни, если наблюдаемые феномены хорошо описываются формулами. И не будем с этим эмпириокритицизмом спорить.

Математики изобретают абстракции и примеряют их к реальности. Отсюда Сингулярность, кротовые норы и пр. экзотика. А может стоит пофантазировать, например и о том, что изменится в наших представлениях о мире, если бы причиной лоренцева сокращения был некий гипотетически предполагаемый физический механизм. Почему бы нет?

Содержание

1.Физическая причина лоренцева сокращения
2.Вывод формулы замедления времени
3.Объяснение феномена постоянства скорости света и пр.
4.Вывод преобразований Лоренца
5.Обоснование принципа относительности и ограничения его применимости
6.Вывод формулы E = Mc² и уравнений динамики
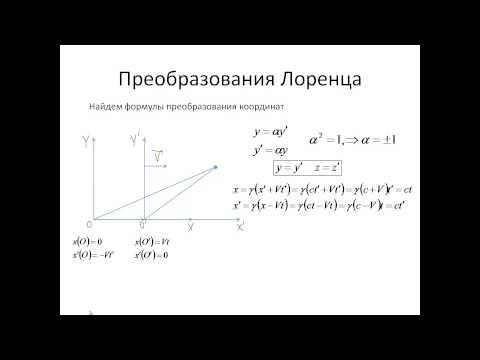
Преобразования Лоренца
Принцип относительности одновременности
Инвариантные величины в СТО
6.3. Преобразования Лоренца
📸 Видео

1.Физическая причина лоренцева сокращения

Сначала выскажу такую, как бы очевидную, сентенцию, что частицы, атомы, молекулы взаимодействуют между собой посредством физических полей. Можно, конечно сказать, что они обмениваются квантовыми частицами, но мы сейчас играем на поле релятивистской теории, поэтому пока забудем о квантах. Итак, первое фантастическое допущение состоит в том, что именно благодаря взаимоуравновешиванию полевых воздействий частицы складываются в определённую конфигурацию и образуют тела. Если какая-то частичка отклонится от положения равновесия, то от неё побежит полевое возмущение, которое сдвинет остальные частицы, что, в свою очередь вызовет обратное полевое воздействие от них на эту частицу.

И, второе допущение, это что полевое возмущение распространяется в некоем общем пространстве с некоей определённой скоростью. А фантастичность этого допущения в том, что по науке поле существует само по себе в 4-х мерном пространстве-времени (П-В) и ни по чему не распространяется. В общем, сложно по науке… Мы предположим, что поля распространяются и существуют в едином 3-х мерном пространстве – в котором находимся мы, Земля и звёзды. Вроде бы сиё само собой разумеется и кто ж этого не знает, однако посмотрим что получится. Кому не интересно заморачиваться с формулами, могут ограничиться чтением только выделенного текста.

Итак, соглашаемся, что между частицами существует время взаимодействия, которое складывается из времени прихода к ним возмущения и времени возвращения отклика от них обратно. А в результате постепенно снова установится прежняя конфигурация тела.
Рис.1 Полевые воздействия, определяющие положение частицы
Для любой точки тела можно выделить группы точек, с которыми у неё будут равные времена взаимодействия и которые назовём изохронными с данной точкой. Ситуация отражена на рис.1. Естественно, что в покое сфера любого радиуса R _покоя вокруг точки является геометрическим местом точек (ГМТ) изохронных с ней.

Заметим, что движение частицы в каждый момент определяется суммой равнодействующих сил, которые прикладываются одновременно от совокупности всех изохронных с ней групп частиц. Попытаемся выяснить как изменится при движении тела поверхность ГМТ, образуемая совокупностью точек 2, 3 и т.д. с одинаковыми временами взаимодействия с точкой 1, которая может уже и не быть сферой.
Пусть точки 1 и 2 тела взаимно неподвижны и синхронно движутся вправо со скоростью V. Когда точка 1 находится в начале координат, посылается полевое возмущение к точке 2. Взаимное расположение точек при этом отмечено литерой A.
Рис.2 Схема полевых взаимодействий точек тела — туда и обратно
Когда возмущение достигнет точки 2, она пройдёт расстояние V∙t₁. Позиции точек при этом отмечены литерой B. За время возврата возмущения от точки 2 к точке 1, точка 2 пройдёт расстояние V∙t₂. Их новые позиции отмечены литерой C.

Формулы (1) описывают по теореме Пифагора расстояния на рис.2, а полученные из них (2) являются уравнениями для вычисления времён t₁ и t₂, значения которых даются формулами (3) и (4) для положительных значений корней, где β=V/c.

Формула (5) даёт значение времени взаимодействия от посылки возмущения до получения отклика.

Из (5) получим уравнение (6) для координат x и y геометрического места изохронных точек, с которыми одинаково время взаимодействия точки 1.
Формула (6) описывает эллипсоид, показанный на рис.3, сжатый вдоль направления движения (вдоль оси X) в √(1 ‑ β 2 ) раз, то есть соответственно формуле Лоренца. Точка 2 на поверхности сферы в покое, при движении сдвинется в положение 2′. При этом материальные точки, бывшие изохронными с точкой 1 в покое, останутся изохронными с ней и при движении.
Рис.3
Итак, при движении материальный объект сжимается по Лоренцу именно потому, что сжимается сама «картинка» физических полей обеспечивающая его целостность в пространстве.

Так как лоренцево сокращение одинаково для всех изохронных точек окружающих каждую точку объекта, то весь движущийся объект одинаково пропорционально сократится вдоль оси движения.

2.Вывод формулы замедления времени

Определим время взаимодействия при движении объекта по сравнению с временем взаимодействия в покое.
Формулы (7) связывают координаты точек при движении с их же координатами при покое в соответствии с
уравнением (6). В формуле (8) вычисляется время взаимодействия при покое. Формулы (9) и (10) получены из формулы (6) при подстановке в неё значений координат x и y и R_покоя из формул (7). Формула (11) эквивалентна (10). Формула (12), полученная из (11) при подстановке в неё левой части формулы (8), связывает времена взаимодействий при покое и при движении. В традиционной форме это отображено в формуле (13), где T₀ обозначен интервал времени между событиями в покоящемся объекте, а T – это интервал времени между теми же событиями в движущемся теле.
Итак, времена взаимодействия всех точек в движущемся объекте увеличиваются в одинаковой пропорции по Лоренцу по сравнению с временем взаимодействия при покое. Соответственно, вообще все процессы в движущемся объекте реально замедляются в таком же отношении.
Причину замедления времени легко понять, если учесть, что возмущение поля от задней из взаимодействующих частиц должно будет догонять переднюю по ходу движения. Когда скорость тела почти сравняется со скоростью света, догонять придётся долго, а при скорости тела равной скорости света, оно её не догонит никогда. Все изменения в теле прекратятся и время в нём как бы остановится.

3.Объяснение феномена постоянства скорости света и пр.

Проведём мысленный эксперимент. Пусть из последнего вагона поезда испускается импульс света, который принимается в его головном вагоне. Мы должны измерить время T₀, которое свет затратит на прохождение поезда известной длины L₀ в его собственной системе. При доказательстве будем использовать предположения об однородности и изотропности пространства, в частности предполагать одинаковые результаты измерения для первой и второй половин поезда, а также для направлений вперёд и назад. Но, строго говоря, эти предположения действенны только в пределах места и времени проведения эксперимента.

Рис.4. Мысленный эксперимент по определению скорости света в движущемся поезде
Для синхронизации момента посылки сигнала из последнего вагона поезда и начала отсчёта счётчика времени в его переднем вагоне используем стартовый импульс света из середины поезда в оба его конца.

Когда стартовый сигнал из середины поезда достигнет его хвоста (время t₁), будет послан импульс света. Когда стартовый сигнал достигнет головы поезда (время t₂), начнётся отсчёт времени до прибытия посланного импульса.
Когда свет распространяется к хвосту, то его скорость суммируется со скоростью поезда, когда к голове – скорость поезда вычитается. Получаем соотношения, приведённые ниже в формулах (1)-(6).
Время T = t₃ — t₂ – это временно́й интервал, который, по мнению наблюдателя в поезде, разделяет события момента посылки сигнала из конца поезда (от момента получения там стартового сигнала) и момента его получения в голове поезда.
Из (6) получим формулу (7), которую преобразуем к виду (8). Далее учтём, что все величины L, T и t здесь измерены в системе отсчёта стороннего наблюдателя в пространстве, где проходит мысленный эксперимент. Но при движении объекта в пространстве его длина, как доказано в гл.1, реально подвергается лоренцеву сокращению, а времена событий, как доказано в гл.2, во столько же раз реально замедляются, т.е. протекают длительнее чем в покое, что и отражено в формулах (9) и (10). Подставляя эти соотношения в формулу (8) для интервала T – времени прохождения света от хвоста до головы поезда, получим соотношение (11).
Но какое отношение эти T₀ и L₀ при покое имеют к собственным времени и длине для тех же событий, измеренным в инерциальной системе отсчёта (ИСО) связанной с движущимся поездом? Очевидно, что они им равны. Дело в том, что время и длина численно выражаются через отношение к эталонам. Соответственно, измерения временны́х и пространственных координат чего-то, сделанные при покое, будут численно равны измерениям того же, сделанным в движущейся ИСО, так как при движении значения и измерений, и эталонов, изменятся пропорционально.
Вопрос в том, как именно они изменяются при движении в пространстве. Мысленный эксперимент с поездом и доказывает, что изменяются они так, что численное значение измеренной в ИСО скорости света остаётся равным значению его скорости в пространстве. Вот именно это не являлось априори очевидным и требовало доказательства.
Мы видим, что «постулат постоянства скорости света» выводится из одного только факта лоренцева сокращения, которое математически выводится из зависимости расположения вещественной материи от скорости распространения и конфигурации физических полей в пространстве.
Для полноты картины определим также скорость света поперёк движения поезда, например между стенками вагона на расстоянии S₀ друг от друга. Для этого измерим время движения светового импульса (2·t₀) туда и обратно. Ввиду очевидной симметричности «туда» и «обратно» рассмотрим только «туда». В системе стороннего наблюдателя движение в пространстве происходит как показано на рис.5.
Отсюда имеем (с·t) 2 = S 2 +(V·t) 2 , откуда получаем t = S/(c·√(1 ‑ β²)), где β=V/c.
В системе поезда прошедшее собственное время t₀ связано с временем прошедшим в пространстве соотношением t = t₀/(√(1 ‑ β²)). Подставляя это выражение в формулу для t в пространстве получим t₀ = S/c.
Рис.5. Мысленный эксперимент по определению скорости света в движущемся поезде/

В собственной системе поезда для этого же t₀ мы имеем соотношение t₀ = S₀/c₀. Но поскольку поперечные размеры при движении не изменяются, т.е. S = S₀, получаем, что и c₀ = c.
Полагаю не нужно доказывать постоянство измеренной скорости света для произвольной ориентации луча, что лишь добавило бы неоправданной сложности. Считая доказанным инвариантность скорости света, нетрудно вывести и преобразования Лоренца (ПЛ), причём без какой-либо апелляции к уравнениям Максвелла или к математически абстрактному пространству Минковского.

4.Вывод преобразований Лоренца

Событие состоит в прибытии светового импульса в точку «E«, находящуюся в неизменных координатах x’ и y’ в системе отсчёта , движущейся со скоростью V относительно неподвижной ИСО , посланного в момент, когда точки O и O’ обеих СО совпадали.
Рис.6.

В собственной СО длине L, измеренной в СО , будет соответствовать координата x’. Для события справедлива система уравнений (1), решая которую получим (2), а затем (3) и (4).
Поскольку длины тел при движении сжимаются по Лоренцу, а скорость света, как доказано в гл.3, одинакова в любой СО, то для собственных x’ и t’ в СО справедливы соотношения (5). Подставив соотношения из (5) в (3) получим (6), а подставив их в (4) получим (7). В силу относительности движения можно считать движущейся систему , но тогда в (6) и (7) надо нештрихованные переменные заменить штрихованными, а скорость V следует взять с обратным знаком, либо просто решить систему относительно x и t.
В результате получим выражения (8) для канонического вида преобразований Лоренца координат и времени событий в разных ИСО.
При использовании ПЛ как чисто формального математического метода, физический механизм феноменов СТО остаётся непроявленным. Поэтому в моих предыдущих статьях о релятивистских эффекте Доплера и аберрации света, а также законах отражения от движущегося наклонного зеркала, ПЛ принципиально не использовались с целью демонстрации именно физической причины этих феноменов.

5.Обоснование принципа относительности и ограничения его применимости

Отметим, что если в покое на схеме рис.1 возмущение от точки 1 до ГМТ изохронных с нею точек приходило одновременно, то при движении, на схеме рис.2, это уже не выполняется. В каждой точке этого ГМТ отклик на возмущение будет создаваться в разные времена, но сойдутся они в точке 1 одновременно. Вопрос в том, будет ли результат от этого такой же как и в покое?

Выше было доказано, что в любой ИСО измеренные собственные времена и расстояния между всеми точками будут такие же, как в покое. Следовательно и количество периодов, например инициированной электромагнитной волны, между любыми точками будет таким же, как и в покое. Поскольку возмущение поля произвольной конфигурации может быть представлено разложением по ряду монохроматических гармоник, то соответственно конфигурации и напряжённости всех полей в собственной системе будут одинаковы им же при покое. Следовательно фазовые соотношения и синхронизация полей, образующих тело, не нарушаются, и все процессы в нём будут протекать как и при покое.

Именно это и провозглашает эйнштейновский «принцип относительности», и, как видим, он математически неизбежно выводится из двух допущений (см. гл.1), напомню: первое: что положение вещественных частиц определяется структурой полей, и второе, что распространение полей происходит с конечной скоростью.

То есть принцип относительности уже как бы вовсе и не априори всеобщий принцип, а следствие, и имеет понятные границы применимости. В частности, скорость света имеет смысл не мировой константы, а является конкретной скоростью света в конкретной области пространства. И кое-где может быть иной вследствие взаимодействия с местными физическими полями, например, гравитацией. Итак, имеем две альтернативы, которые имеют результатом совершенно одинаковые релятивистские формулы:

первая, ортодоксальная и научная: требует постулировать априори истинным принцип относительности;
вторая и фантастическая: предлагает признать зависимость положения вещественной материи от конфигурации и скорости распространения физических полей в пространстве, в том числе связанных с вещественными частицами

.
В первом случае феномены СТО не требуют объяснений, а их причины и механизмы остаются непознаваемы. Вопрос «Почему?» оказывается даже как бы вне науки.
Во втором, допущения вполне даже логичны и ничего постулировать не требуется, а «фантастичны» они лишь постольку, поскольку в науке приняты иные причины релятивизма. На вопрос «почему таковы феномены СТО?» здесь даётся наглядное и даже чуть ли не тривиальное объяснение. Зато возникает насущная потребность выяснить природу материи и в каких она отношениях с физическими полями.

Поэтому продолжим фантазировать дальше.

6.Вывод формулы E = Mc² и уравнений динамики

Сначала выясним, как преобразуются силы при релятивистских скоростях. Выделим в теле элемент объёма, на который действуют уравновешенные моменты сил. При движении тела продольный размер (вдоль траектории движения) выделенного элемента сократится в соответствии с коэффициентом Лоренца. Чтобы элемент остался в равновесии, точно в таком же соотношении должны увеличиться силы, перпендикулярные движению.
Рис.7.
Величина сил параллельных движению не изменится. Фактор зависимости сил от ориентации относительно направления движения следует учитывать при векторном разложении сил в следующих ниже формулах.

Заметим, что разгон тела до некоей скорости осуществляется приложенной силой, которая соответственно при том выполняет некую работу, чем увеличивает энергию тела. А чем в пространстве отличается разогнанное тело от находящегося в покое? Тем, что разогнанное сжато по Лоренцу. В гл.1 выводится формула для геометрического места точек (ГМТ), окружающих данную точку, с которой у них одинаково время взаимодействия физических полей. Это ГМТ оказывается эллипсоидом сжатым по Лоренцу в направлении движения. Обратим теперь внимание на то, что объём W этого эллипсоида уменьшается пропорционально лоренцеву сокращению. Это отражено в формуле (1) ниже. Вот теперь сделаем уже действительно фантастическое предположение, что при ускорении тела работа силы затрачивается на сжатие занимаемого им объёма пространства, который остаётся затем неизменным при свободном движении. По крайней мере, это предположение ничем не хуже научных сентенций, что пространство может искривляться или раздуваться.

Предположим, что эта энергия E обратно пропорциональна объёму, до которого его удалось сжать согласно формуле (2), или (3) после подстановки в неё (1).
E из (3) разложим в ряд Тейлора (4), откуда (5) – приращение энергии от скорости в первом приближении при малых скоростях. Но при малых скоростях оно же равно (6). Сравнивая (5) и (6), получим (7) и (8). Подставляя (8) в (3), получим (9), связывающее энергию тела в сжатом пространстве с его массой покоя.
Релятивистскую массу выразим формулой (10), откуда, подставляя (2), получим известное выражение (11), связывающее массу и энергию. Сравнивая (9) и (11), получим (12).
Масса является просто иной формулировкой энергии затраченной на сжатие пространства. И в этом смысле они эквивалентны. А вещество всего лишь «маркирует» занимаемый телом участок пространства.

Изменение полной энергии E системы, т.е. энергии сжатия пространства, в полном соответствии с ньютоновой классической механикой, равно работе приложенной силы как произведению силы на путь, а изменение импульса P системы равно произведению той же силы на время её действия. Эти зависимости отражены в формулах (13). После подстановки в них выражений для энергии из (11) и импульса P из формулы (14) получаем систему уравнений (15), которая в форме малых приращений записана в (16) в векторной форме. Затем, дифференцируя по времени, запишем систему дифференциальных уравнений (17), описывающих релятивистскую динамику. Силу F дифференцировать не надо, так как она внешняя и не зависит от вариаций переменных системы. Подставив в формулу (A) выражение для массы из (12), получим известную релятивистскую формулу прямолинейного движения (18).
Из системы уравнений (17) можно выяснить зависимость массы от скорости. Подставив F из формулы (B) в формулу (A) и разделив обе части равенства на c², при ускорении вдоль траектории движения, получим выражения (19) и (20). Откуда, интегрируя, получим выражение (21). Легко видеть, что оно эквивалентно прологарифмированному выражению (12) для релятивистской массы, где const равна логарифму от массы покоя m₀. Это значит, что именно такая зависимость массы от скорости обеспечивает соответствие энергии Mc² и импульса M·V, в формулах (16, 17). И отсюда также следует, что величина, принятая нами ранее за массу покоя, является не зависящей от скорости константой, как это и записано в исходных формулах (9). И значит верно наше предположение о зависимости энергии от степени сжатия пространства.

Конечно заявление о сжатии пространства не слишком убедительно. Если пространство предполагается пустым вместилищем частиц и тел, то как можно сжать пустоту? Пустота так и останется пустотой. Наука, правда, позволяет себе говорить об искривлении пустого пространства – формулы того требуют. Однако, строго говоря, её пространство является математической абстракцией.

Но мы вполне обоснованно можем предположить, что пространство не пусто, а заполнено некоей материей, которая, предположим, не в сжатом состоянии воспринимается нами как пустота. Когда же, например, она находится под напряжением сжатия, мы имеем вещественные частицы и тела. Когда оные в ней покоятся, то степень сжатия (энергия) участка этой материи соответствует массе покоя тела, а при его ускорении увеличивается и степень сжатия (энергия) тела, и соответствующая ему масса.

И вот в этой материальной среде вполне могут существовать и распространяться с конкретной скоростью физические поля определяющие местоположение и взаимодействие частиц (вплоть до «самых-самых» первичных – которые, продолжаем фантазировать, окажутся явлением фокусировки полей от окружающей их обстановки без которой они и не существуют), энергия покоя и движения которых определяется степенью сжатия занимаемого ими участка первоматерии. Собственно, уравнения релятивистской динамики как раз и описывают движение этих неоднородностей напряжений (вещественных тел) в первоматерии. Как мы могли видеть, при этом никаких противоречий с опытом Майкельсона и преобразованиями Лоренца не возникает.

Видео:Специальная теория относительности: #3. Преобразования Лоренца [MinutePhysics]Скачать

Преобразования Лоренца

Ранее мы уже изучили формулы, называемые классическими преобразованиями Галилея, однако они несовместимы с постулатами специальной теории относительности (СТО). Поэтому в данном случае нам нужно использовать другие положения. Благодаря новым преобразованиям мы сможем установить, какая связь существует между некоторым моментом события t , наблюдаемого в системе отсчета K в точке с координатами ( x , y , z ) и показателями того же события, которое наблюдается в системе отсчета K ‘ .

Преобразования Лоренца представляют собой кинематические формулы, с помощью которых происходит преобразование координат и времени в специальной теории относительности.

Они были впервые сформулированы еще в 1904 году в качестве преобразований, относительно которых были инвариантны уравнения электродинамики.

Обозначим основные системы K и K ‘ , скорость их движения – υ , а ось, вдоль которой они движутся – x . В таком случае преобразования Лоренца примут следующий вид:

K ‘ → K x = x ‘ + υ t ‘ 1 — β 2 , y = y ‘ , z = z ‘ , t = t ‘ + υ x ‘ / c 2 1 — β 2 . K → K ‘ x ‘ = x — υ t 1 — β 2 , y ‘ = y , z ‘ = z , t ‘ = t — υ x / c 2 1 — β 2 .

Используя эти формулы, мы можем вывести из них множество следствий. Так, именно из системы преобразований Лоренца следует лоренцево сокращение длины и релятивистский эффект замедления времени.

Возьмем случай, когда в системе K ‘ происходит некий процесс, длительность которого составляет τ 0 = t ‘ 2 – t ‘ 1 (по собственному времени). Здесь t ‘ 1 и t ‘ 2 – это время на часах в начале данного процесса и в его конце. Чтобы вычислить его общую продолжительность в точке x , необходимо взять для расчета следующую формулу:

τ = t 2 — t 1 = t ‘ 2 + υ x ‘ / c 2 1 — β 2 — t ‘ 1 + υ x ‘ / c 2 1 — β 2 = t ‘ 2 — t ‘ 1 1 — β 2 = τ 0 1 — β 2 .

Формула релятивистского сокращения длины выводится из преобразований Лоренца точно таким же образом.

Видео:16. Постулаты СТО. Преобразования ЛоренцаСкачать

Принцип относительности одновременности

Еще одно важное следствие, которое необходимо знать, – это положение о том, что любая одновременность относительна.

Например, если в системе отсчета K ‘ взять две разные точки, в которых некий процесс будет протекать одновременно (с позиции стороннего наблюдателя), то в системе наблюдатель будет иметь следующее:

x 1 = x ‘ 1 + υ t ‘ 1 — β 2 , x 2 = x ‘ 2 + υ t ‘ 1 — β 2 ⇒ x 1 ≠ x 2 , t 1 = t ‘ + υ x ‘ 1 / c 2 1 — β 2 , t 2 = t ‘ + υ x ‘ 2 / c 2 1 — β 2 ⇒ t 1 ≠ t 2 .

Из этого вытекает пространственная разобщенность данных событий в системе K , следовательно, они не могут считаться одновременными. Нельзя сразу сказать, какое событие будет происходить первым, а какое вторым, поскольку это определяется особенностями системы отсчета – знак разности будет определен знаком выражения υ ( x ‘ 2 – x ‘ 1 ) .

Если между событиями имеется причинно-следственная связь, то данный вывод специальной теории относительности для них использовать нельзя. Однако мы можем показать, что при этом не нарушается принцип причинности, и события следуют в нужном порядке в любой инерциальной системе отсчета.

Разберем пример, показывающий, что одновременность разобщенных в пространстве событий является относительной.

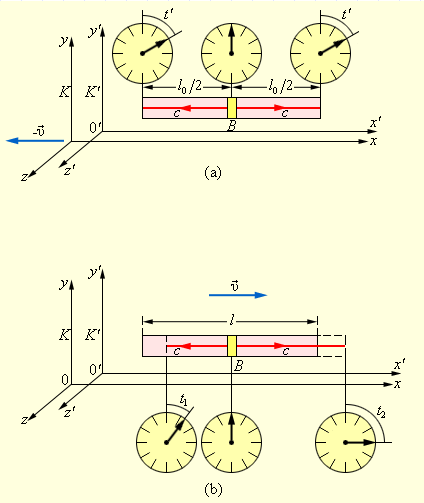
Возьмем систему отсчета K ‘ и расположим в ней длинный жесткий стержень. Его положение будет неподвижным и ориентированным вдоль оси абсцисс. Установим на оба его конца часы, синхронизированные между собой, а в центр поместим импульсную лампу. Также у нас будет система K ‘ , совершающая движение вдоль оси x в системе K .

В определенный момент времени лампа включится и пошлет световые сигналы в направлении обоих концов жесткого стержня. Поскольку она находится точно в центре, эти сигналы должны дойти до концов в одно и то же время t , которое должно быть зафиксировано расположенными на них часами. Однако концы стержня движутся относительно системы K так, что один конец стремится навстречу световому сигналу, а другой конец свету приходится догонять. Скорость света, распространяющегося в оба направления, одинакова, но сторонний наблюдатель скажет, что до левого конца свет дошел быстрее, чем до правого.

Рисунок 4 . 4 . 1 . Иллюстрация принципа относительности одновременности: достижение световым импульсом концов стержня в системе K ‘ в одно и то же время и в системе K в разное.

Видео:Преобразования Лоренца (видео 10) | Специа́льная тео́рия относи́тельностиСкачать

Инвариантные величины в СТО

Данные преобразования нужны нам для выражения относительного характера временных промежутков и промежутков расстояний. Вместе с тем в специальной теории относительности помимо утверждения относительного характера времени и пространства очень важно установить инвариантные физические величины, не изменяющиеся при смене системы отсчета. Подобной величиной является скорость света в вакууме, чей характер в рамках СТО становится абсолютным. Также важна такая величина, как интервал между событиями, поскольку именно она выражает абсолютность пространственно-временной связи.

Для вычисления пространственно-временного интервала необходимо использовать следующую формулу:

s 12 = c 2 t 12 2 — l 12 2 .

В ней с помощью параметра l 12 выражено расстояние между точками одной системы, где совершаются события, а t 12 – это временной промежуток между теми же самыми событиями. Если местом одного из событий является начало координат, т.е. x 1 = y 1 = z 1 = 0 и ( t 1 = 0 ) , а второе происходит в точке с координатами x , y , z в некоторое время t , то формула вычисления пространственно-временного интервала между ними записывается так:

s = c 2 t 2 — x 2 — y 2 — z 2 .

Преобразования Лоренца дают нам возможность доказать неизменность пространственно-временного интервала между событиями при смене инерциальной системы.

Если величина интервала не зависит от того, какая система отсчета используется, т.е. является объективной при любых относительных расстояниях и временных промежутках, то такой интервал называется инвариантным.

Допустим, что у нас есть событие (вспышка света), которое произошло в точке начала координат в некоторой системе во время, равное 0 , а потом свет переместился в другую точку с координатами x , y , z во время t . Тогда мы можем записать следующее:

x 2 + y 2 + z 2 = c 2 t 2 .

У нас получилось, что интервал этой пары событий будет равен нулю. Если мы поменяем систему координат и возьмем другое время для второго события, то результаты окажутся точно такими же, поскольку:

x 2 + y 2 + z 2 = c 2 t 2

Иначе говоря, любые два события, которые связывает между собой световой сигнал, будут иметь нулевой пространственно-временной интервал.

Также формулы Лоренца для времени и координат можно использовать для выведения релятивистского закона сложения скоростей.

Например, у нас есть частица, которая находится в системе отсчета K ‘ и движется в ней вдоль оси абсцисс со скоростью u ‘ x = d x ‘ d t ‘ . Параметры скорости u ‘ x и u ‘ равны 0 . В системе K , соответственно, скорость будет равна u x = d x d t .

Применим к одной из формул преобразования Лоренца операцию дифференцирования и получим следующее:

u x = u ‘ x + υ 1 + υ c 2 u ‘ x , u y = 0 , u z = 0 .

Данные отношения являются выражением релятивистского закона сложения скоростей. Он применим в случае движения частицы параллельно относительной скорости υ → в системах отсчета K и K ‘ .

Если υ ≪ c , то релятивистские отношения могут быть преобразованы в формулы классической механики:

u x = u ‘ x + υ , u y = 0 , u z = 0 .

Если мы имеем дело со световым импульсом, распространяющимся в системе K ‘ вдоль оси x ‘ со скоростью u ‘ x = c , то в этом случае применима следующая формула:

u x = c + υ 1 + υ / c = c , u y = 0 , u z = 0 .

Иначе говоря, скорость распространения светового импульса в системе K вдоль оси x также будет равна c , что соответствует постулату об инвариантности скорости света.

Видео:Преобразования ГалилеяСкачать

6.3. Преобразования Лоренца

Для объяснения отрицательного результат опыта Майкельсона — Морли была выдвинута интересная гипотеза. Сначала Дж. Фитцджеральд, а затем (независимо от него) Г.А. Лоренц попытались объяснить результат опыта тем, что эфирный ветер «давит» на тела и сокращает их размеры вдоль направления движения. Если это так, то в формулах для продольного распространения света в интерферометре надо заменить «истинную» длину пути L на некоторую другую величину L_||. Тогда формула для определения времени, затрачиваемого светом при распространении в направлении, параллельном орбитальной скорости Земли, примет вид

Для совпадения времен

достаточно тогда положить

Гипотеза Лоренца — Фитцджеральда казалась искусственной, изобретенной только для объяснения результатов одного эксперимента.

А между тем у физиков появилась еще одна трудность, не связанная с опытом Майкельсона — Морли. К этому времени сформировалась теория электромагнетизма, воплотившаяся в уравнения Максвелла. И оказалось, что уравнения Максвелла не инвариантны относительно преобразований Галилея. Это означало, что с помощью электромагнитного поля, казалось бы, можно сделать то, что не удалось в опытах Майкельсона — обнаружить движение инерциальной системы. Но тогда пришлось бы отказаться от принципа относительности Галилея, который выглядел весьма убедительно. К тому же свет, использованный в опытах Майкельсона-Морли, это частный случай электромагнитного поля.

Поэтому был поставлен вопрос: а как должны выглядеть преобразования координат от одной системы отсчета к другой, чтобы уравнения Максвелла были инвариантными? Ответ дал в 1904 г. Лоренц, и с тех пор эти преобразования называют его именем (хотя они появлялись ранее в работах других ученых — у В. Фохта в 1887 г. и у Дж. Лармора в 1900 г.).

Из уравнений Максвелла следует, в частности, что свет распространяется со скоростью c. Вернемся снова к двум инерциальным системам отсчета (см. рис. 6.1). Одну мы будем считать неподвижной (К-система). Пусть другая (К’-система) движется относительно К-системы с постоянной скоростью V. Для упрощения будем считать, что оси координат обеих систем параллельны, в начальный момент времени начала отсчета 0 и 0′ совпадают, а затем точка 0′ движется со скоростью V вдоль оси x. Пусть в начальный момент времени t = 0 из точки 0 (совпадающей с точкой 0′ ) вдоль оси х излучается световой импульс. Уравнение его движения имеет вид

Таким же должно быть и его уравнение движения относительно системы отсчета К’ :

Это — частный случай инвариантности уравнений Максвелла, но его рассмотрения достаточно, чтобы вывести преобразования Лоренца.

Мы будем рассуждать так же, как и при выводе преобразований Галилея, учитывая все, что успели с тех пор узнать. При преобразованиях Галилея координата x относительно системы отсчета K складывалась из положения начала отсчета системы K’ (величина Vt) и координаты x’. Но сейчас мы уже не будем предполагать инвариантности длин и потому умножим x’ на некий коэффициент γ. Иными словами, мы предполагаем пропорциональность длин в разных системах отсчета, но не их равенство. Тогда координата x какой-либо материальной точки связана с координатой x’ этой же точки соотношением

Коэффициент γ пока неизвестен, а отрезок Vt — расстояние между точками 0 и 0′ в момент времени t, измеряемый по часам системы K.

Если система K’ движется относительно K со скоростью V, то система K движется относительно K’ со скоростью –V. Ввиду равноправности обеих систем отсчета можно написать аналогичную связь между координатами:

Теперь отрезок Vt’ — это расстояние между точками 0 и 0′ в момент времени t’, измеряемый по часам системы K’. Как видно, мы не предполагаем инвариантности интервалов времени, но и не отвергаем такую возможность: если наши уравнения допустят решение

то мы вернемся в лоно классической механики. Как мы увидим, этот вариант не реализуется.

Запишем прямые и обратные преобразования координат так, чтобы в левой и правой частях уравнений стояли координаты и времена, относящиеся к одной системе отсчета. Для этого выразим x через x’, t’ с помощью второго уравнения, подставим это выражение в первое уравнение и найдем оттуда t. Получаем в итоге:

Применим теперь полученные преобразования координат и времени к законам движения светового импульса в системе отсчета K. Подставим найденные выражения для x, t в уравнение движения светового импульса

Чтобы это уравнение имело вид

выражение в скобках должно быть равно единице, то есть

Подставляя выражение для γ в найденные выше преобразования координат и времени, получаем преобразования Лоренца. Их надо дополнить соотношениями

которые в точности совпадают с тем, что было в преобразованиях Галилея. Для получения обратных преобразований достаточно поменять знак у скорости V.

общепринято называть релятивистским фактором (множителем). С учетом этого обозначения преобразования Лоренца, оставляющие инвариантными уравнения теории электромагнетизма, имеют вид: