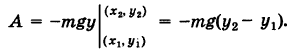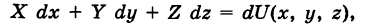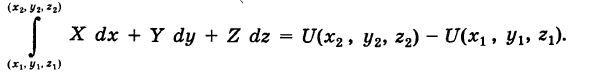В этой теме мы рассмотрим метод восстановления функции по ее полному дифференциалу, дадим примеры задач с полным разбором решения.
Бывает так, что дифференциальные уравнения (ДУ) вида P ( x , y ) d x + Q ( x , y ) d y = 0 могут содержать в левых частях полные дифференциалы некоторых функций. Тогда мы можем найти общий интеграл ДУ, если предварительно восстановим функцию по ее полному дифференциалу.
Рассмотрим уравнение P ( x , y ) d x + Q ( x , y ) d y = 0 . В записи левой его части содержится дифференциал некоторой функции U ( x , y ) = 0 . Для этого должно выполняться условие ∂ P ∂ y ≡ ∂ Q ∂ x .
Полный дифференциал функции U ( x , y ) = 0 имеет вид d U = ∂ U ∂ x d x + ∂ U ∂ y d y . С учетом условия ∂ P ∂ y ≡ ∂ Q ∂ x получаем:
P ( x , y ) d x + Q ( x , y ) d y = ∂ U ∂ x d x + ∂ U ∂ y d y
∂ U ∂ x = P ( x , y ) ∂ U ∂ y = Q ( x , y )
Преобразовав первое уравнение из полученной системы уравнений, мы можем получить:
U ( x , y ) = ∫ P ( x , y ) d x + φ ( y )
Функцию φ ( y ) мы можем найти из второго уравнения полученной ранее системы:
∂ U ( x , y ) ∂ y = ∂ ∫ P ( x , y ) d x ∂ y + φ y ‘ ( y ) = Q ( x , y ) ⇒ φ ( y ) = ∫ Q ( x , y ) — ∂ ∫ P ( x , y ) d x ∂ y d y
Так мы нашли искомую функцию U ( x , y ) = 0 .
Найдите для ДУ ( x 2 — y 2 ) d x — 2 x y d y = 0 общее решение.
P ( x , y ) = x 2 — y 2 , Q ( x , y ) = — 2 x y
Проверим, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x :
∂ P ∂ y = ∂ ( x 2 — y 2 ) ∂ y = — 2 y ∂ Q ∂ x = ∂ ( — 2 x y ) ∂ x = — 2 y
Наше условие выполняется.
На основе вычислений мы можем сделать вывод, что левая часть исходного ДУ является полным дифференциалом некоторой функции U ( x , y ) = 0 . Нам нужно найти эту функцию.
Так как ( x 2 — y 2 ) d x — 2 x y d y является полным дифференциалом функции U ( x , y ) = 0 , то
∂ U ∂ x = x 2 — y 2 ∂ U ∂ y = — 2 x y
Интегрируем по x первое уравнение системы:
U ( x , y ) = ∫ ( x 2 — y 2 ) d x + φ ( y ) = x 3 3 — x y 2 + φ ( y )
Теперь дифференцируем по y полученный результат:
∂ U ∂ y = ∂ x 3 3 — x y 2 + φ ( y ) ∂ y = — 2 x y + φ y ‘ ( y )
Преобразовав второе уравнение системы, получаем: ∂ U ∂ y = — 2 x y . Это значит, что
— 2 x y + φ y ‘ ( y ) = — 2 x y φ y ‘ ( y ) = 0 ⇒ φ ( y ) = ∫ 0 d x = C
где С – произвольная постоянная.
Получаем: U ( x , y ) = x 3 3 — x y 2 + φ ( y ) = x 3 3 — x y 2 + C . Общим интегралом исходного уравнения является x 3 3 — x y 2 + C = 0 .
Разберем еще один метод нахождения функции по известному полному дифференциалу. Он предполагает применение криволинейного интеграла от фиксированной точки ( x 0 , y 0 ) до точки с переменными координатами ( x , y ) :
U ( x , y ) = ∫ ( x 0 , y 0 ) ( x , y ) P ( x , y ) d x + Q ( x , y ) d y + C
В таких случаях значение интеграла никак не зависит от пути интегрирования. Мы можем взять в качестве пути интегрировании ломаную, звенья которой располагаются параллельно осям координат.
Найдите общее решение дифференциального уравнения ( y — y 2 ) d x + ( x — 2 x y ) d y = 0 .
Проведем проверку, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x :
∂ P ∂ y = ∂ ( y — y 2 ) ∂ y = 1 — 2 y ∂ Q ∂ x = ∂ ( x — 2 x y ) ∂ x = 1 — 2 y
Получается, что левая часть дифференциального уравнения представлена полным дифференциалом некоторой функции U ( x , y ) = 0 . Для того, чтобы найти эту функцию, необходимо вычислить криволинейный интеграл от точки ( 1 ; 1 ) до ( x , y ) . Возьмем в качестве пути интегрирования ломаную, участки которой пройдут по прямой y = 1 от точки ( 1 , 1 ) до ( x , 1 ) , а затем от точки ( x , 1 ) до ( x , y ) :
∫ ( 1 , 1 ) ( x , y ) y — y 2 d x + ( x — 2 x y ) d y = = ∫ ( 1 , 1 ) ( x , 1 ) ( y — y 2 ) d x + ( x — 2 x y ) d y + + ∫ ( x , 1 ) ( x , y ) ( y — y 2 ) d x + ( x — 2 x y ) d y = = ∫ 1 x ( 1 — 1 2 ) d x + ∫ 1 y ( x — 2 x y ) d y = ( x y — x y 2 ) y 1 = = x y — x y 2 — ( x · 1 — x · 1 2 ) = x y — x y 2
Мы получили общее решение дифференциального уравнения вида x y — x y 2 + C = 0 .
Определите общее решение дифференциального уравнения y · cos x d x + sin 2 x d y = 0 .
Проверим, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x .
Так как ∂ ( y · cos x ) ∂ y = cos x , ∂ ( sin 2 x ) ∂ x = 2 sin x · cos x , то условие выполняться не будет. Это значит, что левая часть дифференциального уравнения не является полным дифференциалом функции. Это дифференциальное уравнение с разделяющимися переменными и для его решения подходят другие способы решения.
- Интегрирование уравнения в полных дифференциалах с помощью криволинейного интеграла второго рода
- Контакты
- Криволинейные интегралы — определение и вычисление с примерами решения
- Криволинейные интегралы
- Криволинейный интеграл первого рода
- Физический смысл криволинейного интеграла второго рода
- Условие независимости криволинейного интеграла второго рода от вида пути интегрирования
- Работа потенциальной силы
- Вычисление криволинейных интегралов: теория и примеры
- Понятие криволинейного интеграла
- Криволинейные интегралы первого рода
- Криволинейные интегралы второго рода
- Вычисление криволинейных интегралов первого рода
- Кривая дана в декартовых прямоугольных координатах
- Кривая дана в параметрической форме
- Вычисление криволинейных интегралов второго рода
- Кривая дана в декартовых прямоугольных координатах
- Кривая дана в параметрической форме
- Больше примеров вычисления криволинейных интегралов
- Вычисление длины дуги кривой
- Вычисление площади участка плоскости
- Вычисление площади цилиндрической поверхности
- Вычисление массы материальной кривой
- Определение статических моментов материальной кривой
- Вычисление моментов инерции материальной кривой
- Вычисление координат центра тяжести материальной кривой
- Вычисление работы силы
- 🔍 Видео
Видео:Математический анализ, 48 урок, Криволинейные интегралы второго родаСкачать

Интегрирование уравнения в полных дифференциалах с помощью криволинейного интеграла второго рода
Запрошуємо усіх хто любить цікаві задачі та головоломки відвідати групу! Зараз діє акція — підтримай студента! Знижки на роботи + безкоштовні консультації.
Контакты
 |
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Двойные и тройные интегралы
- Делимость чисел в математике
- Обыкновенные дроби
- Отношения и пропорции
- Уравнения поверхности и линии в пространстве
- Общее уравнение плоскости
- Угол между плоскостями
- Понятие о производной вектор-функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Криволинейный интеграл II рода вдоль плоской кривойСкачать

Вычисление криволинейных интегралов: теория и примеры
Видео:Уравнение в полных дифференциалахСкачать

Понятие криволинейного интеграла
Криволинейные интегралы — обобщение понятия определённого интеграла на случай, когда областью интегрирования является отрезок некоторой кривой, лежащий в плоскости. Общая запись криволинейного интеграла следующая:
где f(x, y) — функция двух переменных, а L — кривая, по отрезку AB которой происходит интегрирование. Если подынтегральная функция равна единице, то криволинейный интеграл равен длине дуги AB.
Как всегда в интегральном исчислении, криволинейный интеграл понимается как предел интегральных сумм каких-то очень маленьких частей чего-то очень большого. Что же суммируется в случае криволинейных интегралов?
Пусть на плоскости расположен отрезок AB некоторой кривой L, а функция двух переменных f(x, y) определена в точках кривой L. Пусть мы выполняем с этим отрезком кривой следующий алгоритм.
- Разделить кривую AB на части точками (рисунки ниже).
- В каждой части свободно выбрать точку M.
- Найти значение функции в выбранных точках.
- Значения функции умножить на
- длины частей в случае криволинейного интеграла первого рода;
- проекции частей на ось координат в случае криволинейного интеграла второго рода.
- Найти сумму всех произведений.
- Найти предел найденной интегральной суммы при условии, что длина самой длинной части кривой стремится к нулю.
Если упомянутый предел существует, то этот предел интегральной суммы и называется криволинейным интегралом от функции f(x, y) по кривой AB.
Случай криволинейного интеграла
первого рода
Случай криволинейного интеграла
второго рода
Введём следующие ообозначения.
M i (ζ i ; η i ) — выбранная на каждом участке точка с координатами.
f i (ζ i ; η i ) — значение функции f(x, y) в выбранной точке.
Δs i — длина части отрезка кривой (в случае криволинейного интеграла первого рода).
Δx i — проекция части отрезка кривой на ось Ox (в случае криволинейного интеграла второго рода).
d = maxΔs i — длина самой длинной части отрезка кривой.
Криволинейные интегралы первого рода
Исходя из вышеизложенного о пределе интегральных сумм, криволинейный интеграл первого рода записывается так:

Криволинейный интеграл первого рода обладает всеми свойствами, которыми обладает определённый интеграл. Однако есть одно важное различие. У определённого интеграла при перемене местами пределов интегрирования знак меняется на противоположный:

В случае же криволинейного интеграла первого рода не имеет значения, какую из точек кривой AB (A или B) считать началом отрезка, а какую концом, то есть

Криволинейные интегралы второго рода
Исходя из изложенного о пределе интегральных сумм, криволинейный интеграл второго рода записывается так:

В случае криволинейного интеграла второго рода при перемене местами начала и конца отрезка кривой знак интеграла меняется:

При составлении интегральной суммы криволинейного интеграла второго рода значения функции f i (ζ i ; η i ) можно умножать также на проекции частей отрезка кривой на ось Oy. Тогда получим интеграл

На практике обычно используется объединение криволинейных интегралов второго рода, то есть две функции f = P(x, y) и f = Q(x, y) и интегралы

а сумма этих интегралов
называется общим криволинейным интегралом второго рода.
Видео:Видеоурок "Уравнение в полных дифференциалах"Скачать

Вычисление криволинейных интегралов первого рода
Вычисление криволинейных интегралов первого рода сводится к вычислению определённых интегралов. Рассмотрим два случая.
Кривая дана в декартовых прямоугольных координатах
Пусть на плоскости задана кривая y = y(x) и отрезку кривой AB соответствует изменение переменной x от a до b. Тогда в точках кривой подынтегральная функция f(x, y) = f(x, y(x)) («игрек» должен быть выражен через «икс»), а дифференциал дуги 

Если интеграл проще интегрировать по y, то из уравнения кривой нужно выразить x = x(y) («икс» через «игрек»), где 

Пример 1. Вычислить криволинейный интеграл

где AB — отрезок прямой между точками A(1; −1) и B(2; 1) .
Решение. Составим уравнение прямой AB , используя формулу 

Из уравнения прямой выразим y через x :

Тогда 
Кривая дана в параметрической форме
Пусть в пространстве задана кривая
Тогда в точках кривой функцию нужно выразить через параметр t (

Аналогично, если на плоскости задана кривая

то криволинейный интеграл вычисляется по формуле

Пример 2. Вычислить криволинейный интеграл

где L — часть линии окружности

находящаяся в первом октанте.
Решение. Данная кривая — четверть линии окружности, расположенная в плоскости z = 3 . Она соответствует значениям параметра 

то дифференциал дуги
Подынтегральную функцию выразим через параметр t :

Теперь, когда у нас всё выражено через параметр t , можем свести вычисление данного криволинейного интеграла к определённому интегралу:
Видео:Криволинейный интеграл по длине дуги ➜ Криволинейный интеграл 1-го родаСкачать

Вычисление криволинейных интегралов второго рода
Так же, как и в случае криволинейных интегралов первого рода, вычисление интегралов второго рода сводится к вычислению определённых интегралов.
Кривая дана в декартовых прямоугольных координатах
Пусть дана кривая на плоскости уравнением функции «игрек», выраженной через «икс»: y = y(x) и дуге кривой AB соответствует изменение x от a до b . Тогда в подынтегральную функцию подставим выражение «игрека» через «икс» и определим дифференциал этого выражения «игрека» по «иксу»: 
Аналогично вычисляется криволинейный интеграл второго рода, когда кривая дана уравнением функции «икс», выраженной через «игрек»: x = x(y) , 
Пример 3. Вычислить криволинейный интеграл

а) Вычислим криволинейный интеграл по отрезку прямой (на рисунке — синяя). Напишем уравнение прямой и выразим «игрек» через «икс»:

Получаем dy = dx . Решаем данный криволинейный интеграл:
б) если L — дуга параболы y = x² , получим dy = 2xdx . Вычисляем интеграл:
В только что решённом примере получили в двух случаях один и тот же результат. И это не совпадение, а результат закономерности, так как данный интеграл удовлетворяет условиям следующей теоремы.
Теорема. Если функции P(x,y) , Q(x,y) и их частные производные 


Кривая дана в параметрической форме
Пусть в пространстве дана кривая


а в подынтегральные функции подставим

выражения этих функций через параметр t . Получаем формулу для вычисления криволинейного интеграла:
Пример 4. Вычислить криволинейный интеграл

отвечающая условию y ≥ 0 .
Решение. Данная кривая — часть эллипса, находящаяся в плоскости z = 2 . Она соответствует значению параметра 

можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:
Если дан криволинейный интеграл и L — замкнутая линия, то такой интеграл называется интегралом по замкнутому контуру и его проще вычислить по формуле Грина.
Видео:12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать

Больше примеров вычисления криволинейных интегралов
Пример 5. Вычислить криволинейный интеграл

где L — отрезок прямой 
Решение. Определим точки пересечения прямой с осями координат. Подставив в уравнение прямой y = 0 , получим 



Из уравнения прямой выразим y :



Теперь можем представить криволинейный интеграл в виде определённого интеграла и начать вычислять его:
В подынтегральном выражении выделяем множитель 
Пример 6. Вычислить криволинейный интеграл

где L — дуга параболы 
Решение. Так как 

Теперь можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:
Пример 7. Вычислить криволинейный интеграл

где L — дуга астроиды
в первом квадранте.
Решение. В первом квадранте 
Представляем криволинейный интеграл в виде определённого интеграла и вычисляем его:
Пример 8. Вычислить криволинейный интеграл

где L — первая арка циклоиды
Решение. Циклоида образует первую арку при изменении параметра t от 0 до 2π . Определим дифференциал дуги:

Подставим в криволинейный интеграл dl и y , выраженные через параметр t и получаем:
Пример 9. Вычислить криволинейный интеграл

где L — отрезок прямой от точки A(1; 1) до точки B(3; 5) .
Решение. Составим уравнение прямой AB :

Из полученного уравнения прямой выразим «игрек»:
Поэтому 
Пример 10. Вычислить криволинейный интеграл

где L — первая арка циклоиды
Решение. Из уравнений кривой следует

Так как циклоида образует первую арку при изменении параметра t от 0 до 2π , то получаем соответствующие пределы интегрирования. Решаем данный криволинейный интеграл:

Уравнением кривой M 0 M 1 является y = 1 , тогда dy = 0 , на кривой M 1 M x — константа, значит, dx = 0 . Продолжаем и завершаем решение:
Вычисление длины дуги кривой
Если подынтегральная функция равна единице, то криволинейный интеграл первого рода равен длине дуги кривой L:

Пример 12. Вычислить длину дуги кривой

где 
Решение. Составляем криволинейный интеграл первого рода:

Определим производную «игрека»:

Продолжаем и завершаем решение:
Вычисление площади участка плоскости
Если границей участка D плоскости является кривая L, то площадь участка D можно вычислить в виде криволинейного интеграла второго рода

Пример 13. Вычислить площадь участка плоскости, ограниченного эллипсом

Решение. Площадь участка плоскости можно вычислить как криволинейный интеграл второго рода

где L — замкнутая линия, ограничивающая участок. Так как

Вычисление площади цилиндрической поверхности
Пусть на плоскости xOy дана гладка кривая L, в точках которой определена непрерывная функция двух переменных 


Вычисление массы материальной кривой
Если L — материальная кривая с плотностью 
Определение статических моментов материальной кривой
Статические моменты материальной кривой с плотностью 


Вычисление моментов инерции материальной кривой
Моменты инерции материальной кривой с плотностью 



Вычисление координат центра тяжести материальной кривой
Координаты центра тяжести 



Вычисление работы силы
Если под воздействием переменной силы 

Пример 14. В каждой точке плоскости действует сила 

Решение. Работу силы вычислим как криволинейный интеграл второго рода

Используя уравнение параболы, производим замену переменной
🔍 Видео
Криволинейный интеграл 2 родаСкачать

Независимость криволинейного интеграла 2 рода от пути интегрированияСкачать

Криволинейный интеграл первого родаСкачать

Уравнение в полных дифференциалахСкачать

Дифференциальные уравнения, 6 урок, Уравнения в полных дифференциалахСкачать

Уравнения в полных дифференциалахСкачать

Криволинейный интеграл 2-го рода.Работа.ВидеоСкачать

Криволинейный интеграл 1 родаСкачать

Формула ГринаСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Криволинейный интеграл 2 рода это просто. Вычисляем криволинейный интеграл 2 рода.Скачать



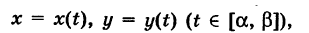
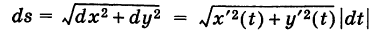
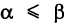 , то dt > 0 и
, то dt > 0 и 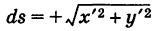 ; если же
; если же 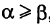 , то dt 2 . Так как парабола проходит через точку
, то dt 2 . Так как парабола проходит через точку 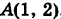 , то 2 = k — 1 2 и, значит, k = 2, т. е. у = 2х 2 . Отсюда dу = 4х dx и
, то 2 = k — 1 2 и, значит, k = 2, т. е. у = 2х 2 . Отсюда dу = 4х dx и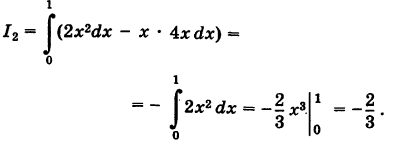
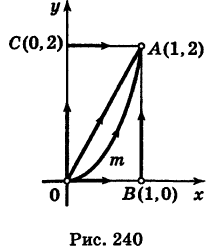
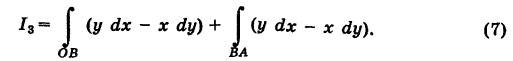
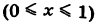 , то
, то 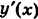 = 0. Далее, уравнение ВА записывается так: х = 1
= 0. Далее, уравнение ВА записывается так: х = 1 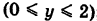 ; поэтому х'(у) = 0. Из формулы (7) получаем
; поэтому х'(у) = 0. Из формулы (7) получаем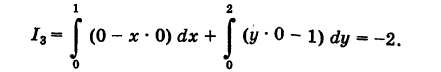
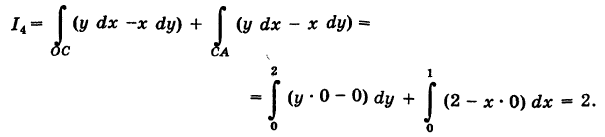
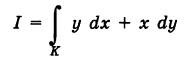
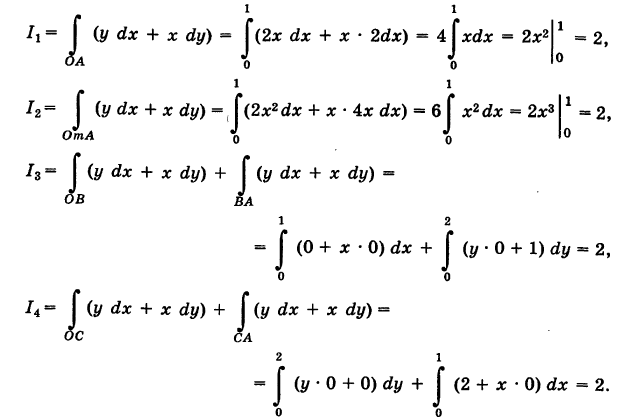
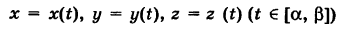
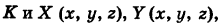
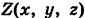 — тройка функций, непрерывных на кривой К, то под соответствующим криволинейным интегралом второго рода понимается интеграл
— тройка функций, непрерывных на кривой К, то под соответствующим криволинейным интегралом второго рода понимается интеграл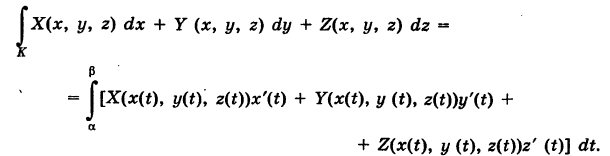
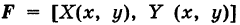 — непрерывно меняющаяся переменная сила и
— непрерывно меняющаяся переменная сила и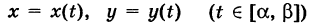
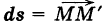 бесконечно малый вектор перемещения из текущей точки М (х, у) кривой К в бесконечно близкую точку
бесконечно малый вектор перемещения из текущей точки М (х, у) кривой К в бесконечно близкую точку 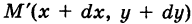 (мы здесь пренебрегаем бесконечно малыми высшего порядка по сравнению с ds). Имеем ds = . Так как на бесконечно малом пути ds непрерывную силу F можно считать постоянной, то элементарная работа силы равна
(мы здесь пренебрегаем бесконечно малыми высшего порядка по сравнению с ds). Имеем ds = . Так как на бесконечно малом пути ds непрерывную силу F можно считать постоянной, то элементарная работа силы равна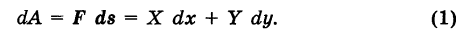
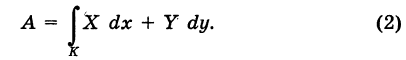
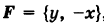 , точка приложения которой описывает параболу ОВ (рис. 242)
, точка приложения которой описывает параболу ОВ (рис. 242)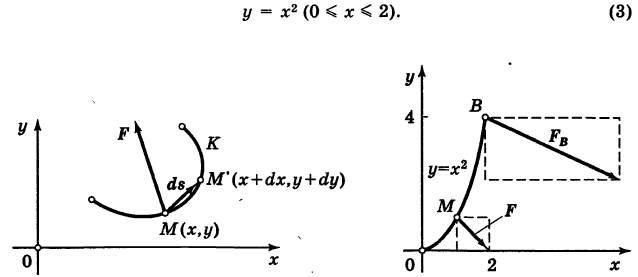
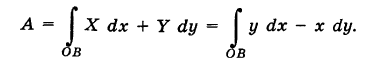
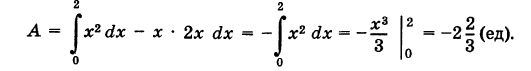
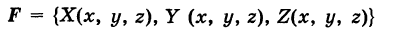
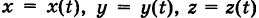 выражается криволинейным интегралом второго рода
выражается криволинейным интегралом второго рода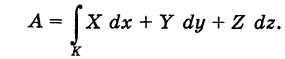
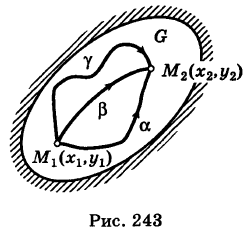
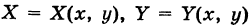 — непрерывные функции в области G (рис. 243). Рассмотрим две произвольные точки
— непрерывные функции в области G (рис. 243). Рассмотрим две произвольные точки 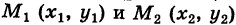 области и всевозможные пути
области и всевозможные пути 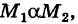
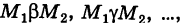 соединяющие эти точки (М1 — начало пути, М2 — конец пути) и не выходящие за пределы области G. Может случиться, что
соединяющие эти точки (М1 — начало пути, М2 — конец пути) и не выходящие за пределы области G. Может случиться, что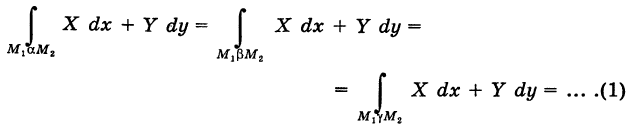
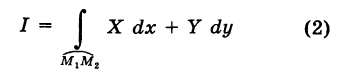
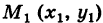 и его конечную точку М2
и его конечную точку М2 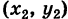 пути. Поэтому здесь употребляется обозначение
пути. Поэтому здесь употребляется обозначение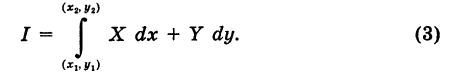
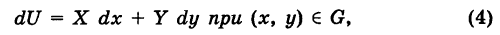
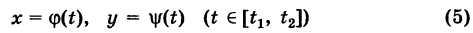
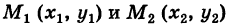 , причем
, причем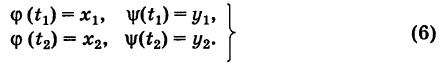
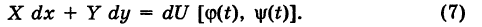
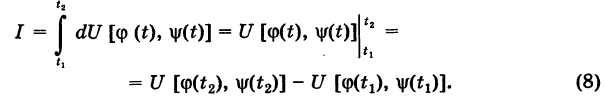
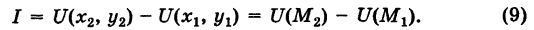
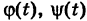 , и, следовательно, интеграл I не зависит от вида пути, соединяющего точки
, и, следовательно, интеграл I не зависит от вида пути, соединяющего точки 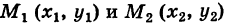
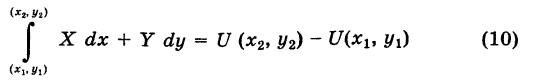
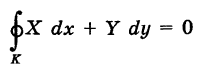
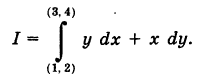
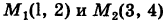 , имеем
, имеем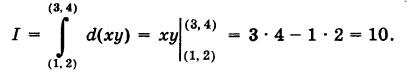
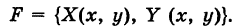
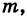 находящуюся на расстоянии г от притягивающего центра, согласно закону Ньютона действует сила
находящуюся на расстоянии г от притягивающего центра, согласно закону Ньютона действует сила 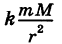 (k — гравитационная постоянная), направленная к притягивающему центру. Другим примером силового поля служит электрическое поле Кулона.
(k — гравитационная постоянная), направленная к притягивающему центру. Другим примером силового поля служит электрическое поле Кулона.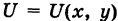 такая, что
такая, что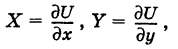
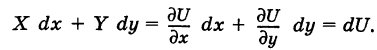
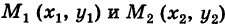 , имеем
, имеем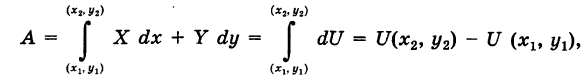
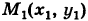 в положение
в положение 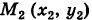 (рис. 244).
(рис. 244).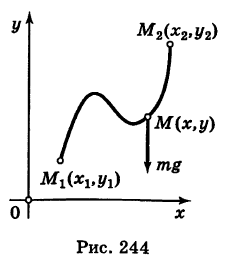
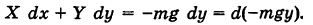
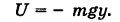
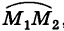 , равна
, равна