Химическим равновесием называется такое состояние обратимой химической реакции
при котором с течением времени не происходит изменения концентраций реагирующих веществ в реакционной смеси. Состояние химического равновесия характеризуется константой химического равновесия:
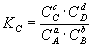
где Ci – концентрации компонентов в равновесной идеальной смеси.
Константа равновесия может быть выражена также через равновесные мольные доли Xi компонентов:
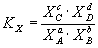
Для реакций, протекающих в газовой фазе, константу равновесия удобно выражать через равновесные парциальные давления Pi компонентов:
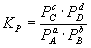
Константа равновесия связана с rG o химической реакции:
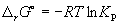
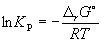
Изменение rG или rF в химической реакции при заданных (не обязательно равновесных) парциальных давлениях Pi или концентрациях Ci компонентов можно рассчитать по уравнению изотермы химической реакции (изотермы Вант-Гоффа):
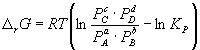
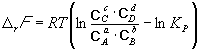
Согласно принципу Ле Шателье, если на систему, находящуюся в равновесии, оказать внешнее воздействие, то равновесие сместится так, чтобы уменьшить эффект внешнего воздействия. Так, повышение давления сдвигает равновесие в сторону уменьшения количества молекул газа. Добавление в равновесную смесь какого-либо компонента реакции сдвигает равновесие в сторону уменьшения количества этого компонента. Повышение (или понижение) температуры сдвигает равновесие в сторону реакции, протекающей с поглощением (выделением) теплоты.
Количественно зависимость константы равновесия от температуры описывается уравнением изобары химической реакции (изобары Вант-Гоффа)
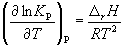
и изохоры химической реакции (изохоры Вант-Гоффа)
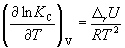
Интегрирование уравнения (9.9) в предположении, что rH реакции не зависит от температуры (что справедливо в узких интервалах температур), дает:
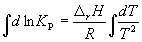
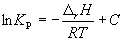
где C – константа интегрирования. Таким образом, зависимость ln KP от 1/Т должна быть линейной, а наклон прямой равен – rH /R.
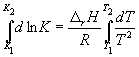
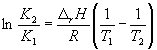
По этому уравнению, зная константы равновесия при двух разных температурах, можно рассчитать rH реакции. Соответственно, зная rH реакции и константу равновесия при одной температуре, можно рассчитать константу равновесия при другой температуре.
ПРИМЕРЫ
Пример 9-1. Рассчитать константу равновесия для реакции
при 500 K. fG o для CO(г) и CH3OH(г) при 500 К равны –155.41 кДж . моль –1 и –134.20 кДж . моль –1 соответственно.
Решение. G o реакции:
rG o = fG o (CH3OH) – fG o (CO) = –134.20 – (–155.41) = 21.21 кДж . моль –1 .
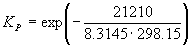
Пример 9-2. Константа равновесия реакции
равна KP = 1.64 10 –4 при 400 o C. Какое общее давление необходимо приложить к эквимолярной смеси N2 и H2, чтобы 10% N2 превратилось в NH3? Газы считать идеальными.
Решение. Пусть прореагировало моль N2. Тогда
| N2(г) | + | 3H2(г) | = | 2NH3(г) |
| Исходное количество | 1 | 1 | ||
| Равновесное количество | 1– | 1–3 | 2 (Всего: 2–2 ) | |
| Равновесная мольная доля: | 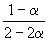 | 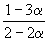 | 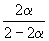 |
Следовательно, KX = 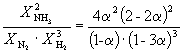
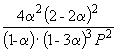
Подставляя = 0.1 в полученную формулу, имеем
1.64 10 –4 =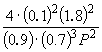
Пример 9-3. Константа равновесия реакции
при 500 K равна KP = 6.09 10 –3 . Реакционная смесь, состоящая из 1 моль CO, 2 моль H2 и 1 моль инертного газа (N2) нагрета до 500 K и общего давления 100 атм. Рассчитать состав равновесной смеси.
Решение. Пусть прореагировало моль CO. Тогда
| CO(г) | + | 2H2(г) | = | CH3OH(г) | |
| Исходное количество: | 1 | 2 | 0 | ||
| Равновесное количество: | 1– | 2–2 | |||
| Всего в равновесной смеси: | 3–2 моль компонентов + 1 моль N2 = 4–2 моль | ||||
| Равновесная мольная доля | 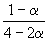 | 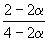 | 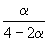 | ||
Следовательно, KX = 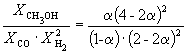
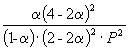
Таким образом, 6.09 10 –3 = 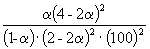
Решая это уравнение, получаем = 0.732. Соответственно, мольные доли веществ в равновесной смеси равны: 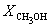
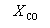
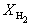
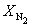
Пример 9-4. Для реакции
при 298 К KP = 6.0 10 5 , а fH o (NH3) = –46.1 кДж . моль –1 . Оценить значение константы равновесия при 500 К.
Решение. Стандартная мольная энтальпия реакции равна
rH o = 2 fH o (NH3) = –92.2 кДж . моль –1 .
Согласно уравнению (9.14), 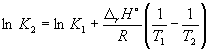
= ln (6.0 10 5 ) + 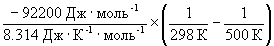
Отметим, что константа равновесия экзотермической реакции уменьшается с ростом температуры, что соответствует принципу Ле Шателье.
ЗАДАЧИ
Указание: во всех задачах считать газы идеальными.
- При 1273 К и общем давлении 30 атм в равновесной смеси
содержится 17% (по объему) CO2. Сколько процентов CO2 будет содержаться в газе при общем давлении 20 атм? При каком давлении в газе будет содержаться 25% CO2?
При 2000 o C и общем давлении 1 атм 2% воды диссоциировано на водород и кислород. Рассчитать константу равновесия реакции
Константа равновесия реакции
при 500 o C равна Kp = 5.5. Смесь, состоящая из 1 моль CO и 5 моль H2O, нагрели до этой температуры. Рассчитать мольную долю H2O в равновесной смеси.
Константа равновесия реакции
при 25 o C равна Kp = 0.143. Рассчитать давление, которое установится в сосуде объемом 1 л, в который поместили 1 г N2O4 при этой температуре.
Сосуд объемом 3 л, содержащий 1.79 10 –2 моль I2, нагрели до 973 K. Давление в сосуде при равновесии оказалось равно 0.49 атм. Считая газы идеальными, рассчитать константу равновесия при 973 K для реакции
при 250 o C rG o = –2508 Дж . моль –1 . При каком общем давлении степень превращения PCl5 в PCl3 и Cl2 при 250 o C составит 30%?
константа равновесия KP = 1.83 10 –2 при 698.6 К. Сколько граммов HI образуется при нагревании до этой температуры 10 г I2 и 0.2 г H2 в трехлитровом сосуде? Чему равны парциальные давления H2, I2 и HI?
Сосуд объемом 1 л, содержащий 0.341 моль PCl5 и 0.233 моль N2, нагрели до 250 o C. Общее давление в сосуде при равновесии оказалось равно 29.33 атм. Считая все газы идеальными, рассчитать константу равновесия при 250 o C для протекающей в сосуде реакции
Константа равновесия реакции
при 500 K равна KP = 6.09 10 –3 . Рассчитать общее давление, необходимое для получения метанола с 90% выходом, если CO и H2 взяты в соотношении 1: 2.
находится в равновесии при 500 K и 10 бар. Если газы идеальные, как повлияют на выход метанола следующие факторы: а) повышение T; б) повышение P; в) добавление инертного газа при V = const; г) добавление инертного газа при P = const; д) добавление H2 при P = const?
устанавливается при 227 o C и общем давлении 1.0 бар, когда парциальное давление NOCl равно 0.64 бар (изначально присутствовал только NOCl). Рассчитать rG o для реакции. При каком общем давлении парциальное давление Cl2 будет равно 0.10 бар?
Рассчитать общее давление, которое необходимо приложить к смеси 3 частей H2 и 1 части N2, чтобы получить равновесную смесь, содержащую 10% NH3 по объему при 400 o C. Константа равновесия для реакции
при 400 o C равна K = 1.60 10 –4 .
При 250 o C и общем давлении 1 атм PCl5 диссоциирован на 80% по реакции
Чему будет равна степень диссоциации PCl5, если в систему добавить N2, чтобы парциальное давление азота было равно 0.9 атм? Общее давление поддерживается равным 1 атм.
При 2000 o C для реакции
Kp = 2.5 10 –3 . В равновесной смеси N2, O2, NO и инертного газа при общем давлении 1 бар содержится 80% (по объему) N2 и 16% O2. Сколько процентов по объему составляет NO? Чему равно парциальное давление инертного газа?
а) увеличивается в 2 раза, б) уменьшается в 2 раза при изменении температуры от 298 К до 308 К.
При 420 o C давление газов равно 5.16 10 4 Па, а при 450 o C 10.8 10 4 Па. Рассчитать константы равновесия при этих температурах и энтальпию диссоциации на моль HgO.
получены следующие данные по зависимости константы равновесия от температуры:
3.98 10 –4
1.41 10 –2
1.86 10 –1
Определить стандартную энтальпию реакции в этом температурном интервале.
ln K = –1.04 –1088 /T +1.51 10 5 /T 2 .
Рассчитать rG o , rH o и rS o реакции при 400 К.


Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору
- Расчет теплового эффекта реакции по температурным зависимостям констант равновесия
- Общая химическая технология. Химические процессы и реакторы (стр. 3 )
- Глава 3 ИСПОЛЬЗОВАНИЕ ЗАКОНОВ ХИМИЧЕСКОЙ КИНЕТИКИ ПРИ ВЫБОРЕ ТЕХНОЛОГИЧЕСКОГО РЕЖИМА И МОДЕЛИРОВАНИИ ХИМИЧЕСКИХ ПРОЦЕССОВ
- § 3.1. Скорость гомогенных химических реакций
- § 3.2. Зависимость скорости химических реакций от концентрации реагентов. Кинетические уравнения
- § 3.3. Способы изменения скорости простых и сложных реакций
- 📸 Видео
Видео:Решение задач на тему: "Нахождение константы равновесия и равновесных концентраций". 1ч. 10 класс.Скачать

Расчет теплового эффекта реакции по температурным зависимостям констант равновесия
Читайте также:
|
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 |
Увеличивая концентрацию одного из реагентов (создавая его избыток), можно повысить степень превращения другого. Этим широко пользуются в химической технологии, добиваясь полного превращения дорогостоящего компонента сырья.
Во многих случаях смещение равновесия процесса вправо можно осуществить и выводом продуктов из реакционной зоны – уменьшением концентрации продукта. Так, введение в систему водоотнимающих средств (например, H2SO4) позволяет сместить равновесие реакции этерификации вправо:
СН3ОН + СН3СООН 
Влияние температуры. Направление смещения равновесия при изменении температуры зависит от знака теплового эффекта реакции. Повышение температуры всегда благоприятствует накоплению веществ, образующихся в данной реакции с поглощением теплоты, т. е. усиливает эндотермическое направление процесса. Понижение температуры действует в противоположную сторону, т. е. усиливает экзотермическое направление.
При изменении температуры процесса равновесие смещается в направлении, для которого изменение энтропии имеет тот же знак, что и изменение температуры ∆T. Например, для рассмотренной выше реакции синтеза аммиака ∆S 0 и Кр(Т) – возрастающая функция. Если ∆H° 0;
СО + Н2О 
8. Выведите уравнение для расчета равновесной степени превращения реагента А по известной величине Кc (для реакции 2А 
9. Выведите уравнение для расчета равновесной степени превращения реагента А по известным значениям Кр и давления р в системе для реакции А + В 
10. Выведите уравнение для расчета равновесного состава участников реакции синтеза аммиака по известным значениям Kp, и давления p в системе.
11. Рассчитайте константу равновесия для реакции СО2 + С


12. Найдите константу равновесия при температурах 500 и 2000 К для реакции Н2О + СО 


13. Почему можно исключить из выражения для константы равновесия концентрации компонентов, являющихся чистыми твердыми веществами или жидкостями?
Видео:Химия | Тепловой эффект химической реакции (энтальпия)Скачать

Глава 3
ИСПОЛЬЗОВАНИЕ ЗАКОНОВ ХИМИЧЕСКОЙ
КИНЕТИКИ ПРИ ВЫБОРЕ ТЕХНОЛОГИЧЕСКОГО
РЕЖИМА И МОДЕЛИРОВАНИИ
ХИМИЧЕСКИХ ПРОЦЕССОВ
Химическая термодинамика позволяет решать вопрос о направлении протекания химических реакций и оценить предельно достижимые (равновесные) состояния реакционной системы. Однако она не может ответить на вопросы, имеющие чрезвычайно важное практическое значение в химической технологии: как быстро произойдет химическое превращение, за какой промежуток времени будет получено то или иное количество продукта реакции.
Решающее значение при выборе условий проведения химико-технологических процессов имеют вопросы скорости химических превращений, изучаемые химической кинетикой.
Для химической технологии важен конечный результат кинетических исследований – конкретный вид уравнения, позволяющего рассчитывать скорость химической реакции при различных условиях ее проведения. Кинетические уравнения, содержащие необходимую информацию об основных закономерностях химических превращений, являются первоосновой математической модели химического реактора. Без знания кинетических закономерностей невозможно правильно выбрать тип реактора и рассчитать его конструктивные размеры.
Вопросы изучения кинетики химических реакций, определения кинетических параметров подробно рассматриваются в руководствах по физической химии и химической кинетике. Здесь основное внимание будет обращено на практические приложения результатов кинетических исследований.
Видео:Тепловой эффект хим. реакции. Энтальпия. Закон Гесса. Капучинка ^-^Скачать

§ 3.1. Скорость гомогенных химических реакций
Скорость химической реакции wrJ принято выражать количеством (моль) nJ одного из реагентов или продуктов, прореагировавшим (или образовавшимся) в единицу времени τ в единице реакционного пространства.
Для гомогенной химической реакции

где V – реакционный объем.
Скорость химической реакции может быть измерена по любому компоненту, участвующему в реакции. Она всегда положительна, поэтому знак перед производной dnJ /dτ должен определяться тем, является ли вещество J исходным реагентом (тогда dnJ/dτ отрицательна) или продуктом (тогда dnJ/dτ положительна). Иногда нельзя определенно сказать, является ли вещество J реагентом или продуктом. Например, при протекании последовательных реакций
A 
R 
вещество R является продуктом по отношению к первой стадии и реагентом по отношению ко второй. В этом случае необходимо, чтобы знак перед производной находился в определенном соответствии со знаками в кинетическом уравнении (см. § 3.2).
В том случае, если реакция протекает при постоянном объеме, скорость определяют как изменение молярной концентрации с в единицу времени:

Если химическая реакция описывается стехиометрическим уравнением
аА + bB + сС +… 
то изменения количеств реагентов и продуктов , в результате ее протекания связаны между собой соотношениями (1.3). Скорости реакции, определенные по изменению количества различных реагентов в соответствии с уравнениями (3.1) или (3.2), количественно различаются между собой, если не равны стехиометрические коэффициенты у этих реагентов.
В то же время из уравнений (3.1) и (1.3) следует, что для скоростей реакции, рассчитанных по изменению количества разных реагентов или продуктов, будет выполняться условие
Такая ситуация создает некоторые неудобства в количественном определении скорости реакции, так как измеренная по изменению количеств различных реагентов скорость одной и той же реакции будет выражаться различными числовыми значениями. Для устранения этого неудобства далее будем определять скорость реакции по уравнению

где j – стехиометрический коэффициент у компонента J, по которому рассчитывают скорость реакции.
Тогда скорость «приводится к общему знаменателю» и независимо от того, по изменению количества какого конкретного реагента или продукта она определялась, численно будет одинакова, т. е.
Экспериментально скорость химической реакции определяют, изучая изменение во времени количества (или концентрации) некоторого реагента или продукта.
Численно скорость реакции выражают в единицах концентрации, отнесенных к единице времени, например: кмоль·м–3·ч–1; моль·л–1·с–1 и т. д.
Видео:Химическое равновесиеСкачать

§ 3.2. Зависимость скорости химических реакций
от концентрации реагентов. Кинетические уравнения
Скорость химического превращения зависит от большого числа переменных. Результаты экспериментальных исследований различных реакций показали, что на скорость влияют не только факторы, определяющие состояние химического равновесия (температура, давление, состав реакционной системы), но и иные причины, такие, как наличие или отсутствие посторонних веществ, не претерпевающих изменений в результате реакции, условия физической транспортировки реагентов к реакционным центрам и др.
Факторы, оказывающие влияние на скорость химического превращения, обычно подразделяют на две группы:
– чисто кинетические (микрокинетические), определяющие скорость взаимодействия на молекулярном уровне;
– макрокинетические, определяющие влияние на скорость реакции условий транспорта реагентов к зоне реакции, наличия или отсутствия перемешивания, геометрических размеров реактора.
Рассмотрим сначала влияние микрокинетических факторов на скорость химических реакций.
Законы химической кинетики основаны на двух простых принципах (постулатах), впервые установленных при изучении реакций в растворах:
скорость химической реакции пропорциональна концентрациям реагентов;
суммарная скорость нескольких последовательных превращений, широко различающихся по скорости, определяется скоростью наиболее медленной стадии.
Функциональная зависимость скорости химической реакции от концентраций компонентов реакционной смеси
называется кинетическим уравнением реакции.
В химической кинетике принято делить химические реакции на элементарные и неэлементарные (сложные).
Элементарными (одностадийными) называются реакции, осуществление которых связано с преодолением одного энергетического барьера при переходе из одного состояния реакционной системы в другое. Механизм такой реакции соответствует ее стехиометрическому уравнению.
Кинетическое уравнение необратимой элементарной реакции
аА + bB 
в соответствии с первым постулатом, основанном на законе действующих масс, имеет вид

Коэффициент пропорциональности k, входящий в кинетическое уравнение (3.4), называют константой скорости химической реакции. Целочисленные показатели степени а и b у концентраций реагентов А и В в кинетическом уравнении (3.4) для элементарной реакции называются порядками реакции по реагентам соответственно А и В. Их сумма а + b = n называется общим порядком реакции. Для элементарных реакций частные порядки (порядки реакций по отдельным реагентам) равны соответствующим стехиометрическим коэффициентам в уравнении реакции.
Наряду с понятием «порядок реакции» в химической кинетике используют понятие «молекулярность реакции». Молекулярность реакции равняется минимальному числу молекул, одновременно принимающих участие в одном элементарном акте реакции.
Для элементарных реакций порядок равен молекулярности и может иметь значения 1, 2, 3. Порядок (или молекулярность) элементарных реакций не превышает значения 3, так как вероятность одновременного столкновения более чем трех молекул чрезвычайно низка.
Однако большинство химических реакций не являются элементарными: они протекают через ряд промежуточных стадий. Стехиометрическое уравнение неэлементарной (сложной) реакции отражает лишь начальное и конечное состояния данной реакционной системы и не описывает механизм реакции.
Сложную реакцию иногда удобно рассматривать как формально простую, т. е. считать, что она протекает в одну, а не в несколько стадий. Так можно поступить, если в условиях рассматриваемой задачи промежуточные продукты не обнаруживаются.
Для формально простой реакции
аА + bВ + dD 
кинетическое уравнение по аналогии с простой (элементарной) реакцией можно записать в следующем виде:
где частные порядки реакции α, β и δ находят экспериментально. В общем случае α ≠ a, β ≠ b, δ ≠ d, т. е. молекулярность и порядок реакции не совпадают. Полный порядок реакции п = α + β + δ и частные порядки в таком уравнении могут быть целочисленными, но могут быть и дробными, так как закон действующих масс, предполагающий целочисленные показатели степеней у концентраций в кинетическом уравнении, строго применим только к элементарным реакциям.
Наряду с неэлементарными реакциями, которые можно рассматривать как формально простые, существует много сложных реакций, которые явно распадаются на стадии (продукты различных стадий образуются в значительных количествах).
Простейшими типами сложных реакций являются параллельные и последовательные реакции.
В параллельных реакциях взаимодействие одних и тех же реагентов может протекать по различным реакционным путям с образованием различных продуктов. В качестве примера можно указать на параллельные реакции окисления аммиака, продуктами которых могут быть или оксид азота NО, или оксид диазота N2О, или азот N2.
В последовательных реакциях продукт первой реакции является исходным реагентом для второй. Реакция может состоять как из двух, так и из большего числа стадий, следующих друг за другом. Примером таких реакций могут служить реакции расщепления углеводородов с длинной углеродной цепочкой на все более мелкие молекулы.
В случае если известен механизм сложной реакции (элементарные стадии, через которые она протекает), скорость реакции по одному из веществ – ее участников – равна алгебраической сумме скоростей тех элементарных стадий, в которых это вещество принимает участие.
При определении знаков у членов этой суммы удобно пользоваться формальным правилом: производной концентрации данного компонента по времени dcJ /dτ приписывают знак минус независимо от того, является ли компонент J исходным реагентом или продуктом реакции; скорости элементарных стадий, в которых компонент J расходуется (является реагентом), записывают в общей сумме со знаком плюс, скорости стадий, в которых компонент J образуется (является продуктом), – со знаком минус.
Пример 3.1. Составим кинетическое уравнение по веществам R и А – участникам сложной реакции:
Эта реакция состоит из трех стадий. Вторая и третья стадии являются последовательными по отношению к первой и параллельны по отношению друг к другу. Скорость по компоненту R, участвующему во всех трех реакциях,
Скорость по исходному реагенту А, участвующему лишь в первой элементарной стадии,
Пример 3.2. Обратимую реакцию
А+ В 
с точки зрения химической кинетики можно рассматривать как сложную, состоящую из двух стадий:
Поэтому с помощью уравнений
можно записать скорость исчезновения или образования участников этой реакции.
Видео:Химическое равновесие. Константа равновесия. Обратимость реакций.Скачать

§ 3.3. Способы изменения скорости
простых и сложных реакций
Как указывалось, скорость химической реакции зависит от большого числа различных факторов. Из кинетических уравнений следует, прежде всего, что скорость простой реакции пропорциональна концентрациям веществ, являющихся реагентами в данной реакции. Следовательно, для простых реакций увеличение концентрации исходных веществ практически всегда приводит к увеличению скорости (за исключением реакций нулевого порядка, скорость которых не зависит от концентрации).
Если реакция, описываемая стехиометрическим уравнением (I), характеризуется различающимися частными порядками по компонентам А и В, наибольшее влияние на скорость реакции будет оказывать изменение концентрации реагента, имеющего больший частный порядок. Например, если кинетическое уравнение реакции, в которой участвуют два реагента, имеет вид 
Для сложных реакций, в частности для параллельных, вопрос о выборе концентраций реагентов для управления процессом также не является однозначным. Рассмотрим для примера систему из двух параллельных реакций разного порядка (при постоянной температуре):

Говоря об увеличении скорости такой реакции, нужно сначала решить, какая реакция более важна, т. е. какая реакция приводит к образованию нужного целевого продукта. Нас интересует чаще всего не то, насколько быстро израсходуется реагент А, а насколько быстрее будет образовываться целевой продукт по сравнению с побочным.
Пусть в рассматриваемом примере целевым является продукт первой реакции R, а побочным – продукт S.
Для анализа соотношения скоростей целевого и побочных процессов пользуются мгновенной, или дифференциальной, селективностью, равной отношению скорости расходования реагента А на целевую реакцию к общей скорости расходования реагента и на целевую, и на побочные реакции.
Значение дифференциальной селективности в ходе процесса в общем случае не остается постоянным, так как оно определяется отношением скоростей реакций, а скорость реакции по мере ее протекания меняется. Таким образом, дифференциальная селективность характеризует эффективность целевой реакции в некоторый момент времени при некотором значении концентраций реагентов и продуктов и при заданной температуре. Лишь в том случае, когда параметры процесса во времени и пространстве не меняются (это возможно при проведении процесса в стационарном реакторе идеального смешения), φ‘ остается постоянной величиной.
При протекании химической реакции меняются концентрации реагентов и продуктов. Рассмотрим, как при изменении концентрации исходного реагента А для системы параллельных реакций (II) при постоянной температуре процесса меняется дифференциальная селективность φ’.
Пусть целевая реакция имеет по исходному реагенту А порядок n1, а побочная реакция – п2, тогда

Проанализируем зависимость φ‘ от концентрации реагента А. Для удобства преобразуем выражение (3.5):

Здесь 
Очевидно, что φ‘ может быть как возрастающей, так и убывающей функцией от концентрации. Определим характер функции φ‘(сА) по знаку первой производной:

Как видно из уравнения (3.7), знак первой производной зависит от знака 
В этом случае желаемый результат – увеличение скорости образования целевого продукта R по сравнению со скоростью образования побочного продукта S (увеличение дифференциальной селективности φ’) – достигается при использовании исходного реагента высокой концентрации.
Рис. 3.1. Зависимость дифференциальной селективности от концентрации исходного реагента А для параллельных реакций при различных соотношениях порядков реакций n1 и п2: 1 – п1= 1, k1 = 10 ч–1 n2 = 2,5, k2 = 15 м4,5/(кмолъ1,5·ч);
2 – n1 = 2,5, k1 =154,5/(кмолъ1,5·ч); n2 = 1; k2 = 10 ч–1
📸 Видео
Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Подготовка к ЕГЭ по ХимииСкачать

Решение задач на термохимические уравнения. 8 класс.Скачать

Влияние концентрации на скорость химических реакций. 10 класс.Скачать

Обратимость и необратимость химических реакций. Химическое равновесие. 1 часть. 9 класс.Скачать

Обратимые и необратимые реакции | Химическое равновесие и условия его смещенияСкачать

Коробов М. В. - Физическая химия. Часть 1 - Характеристические функцииСкачать

Расчеты по уравнениям химических реакций. 1 часть. 8 класс.Скачать

Использование уравнения Аррениуса для решения задач (1/2). Химия для поступающих.Скачать

Бычков А.Ю. - Физическая геохимия - 13. Физико-химические расчеты. Часть 1Скачать

Лекция 2 Второй закон ТД, равновесиеСкачать

Обратимая реакция второго порядка || Вывод уравнения || Разбор задачи || КинетикаСкачать

Рубин А. Б. - Биофизика I - Термодинамика ферментативных реакцийСкачать

Экзо- и эндотермические реакции. Тепловой эффект химических реакций. 8 класс.Скачать

Успенская И. А. - Химическая термодинамика и кинетика - Константы равновесия изотермических реакцийСкачать

 Химическая термодинамика позволяет определить константу равновесия химической реакции при какой-либо температуре по уравнению изобары или изохоры химической реакции:
Химическая термодинамика позволяет определить константу равновесия химической реакции при какой-либо температуре по уравнению изобары или изохоры химической реакции: Уравнение изохоры химической ре-акции в дифференциальном виде (V=const)
Уравнение изохоры химической ре-акции в дифференциальном виде (V=const)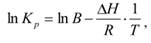 Уравнение, позволяющее рассчитать тепловой эффект химической реакции по константам равновесия при разных температурах:
Уравнение, позволяющее рассчитать тепловой эффект химической реакции по константам равновесия при разных температурах: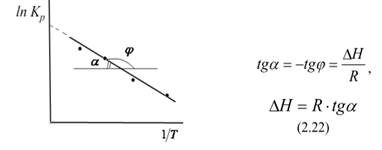 Полученное уравнение представляет собой уравнение прямой в координатах T Kp/1 ln , тангенс угла которой равен отношению теплового эффекта химической реакции к универсальной газовой постоянной. Эту зависимость можно использовать для графического нахождения теплового эффекта химической реакции:
Полученное уравнение представляет собой уравнение прямой в координатах T Kp/1 ln , тангенс угла которой равен отношению теплового эффекта химической реакции к универсальной газовой постоянной. Эту зависимость можно использовать для графического нахождения теплового эффекта химической реакции: Давление влияет на химическое равновесие в газовой фазе и равновесие гетерогенных реакций с участием газообразных веществ. Для выяснения зависимости константы равновесия от давления используется константа равновесия, выраженная через мольные доли компонентов К х (К р и К с от давления не зависят).
Давление влияет на химическое равновесие в газовой фазе и равновесие гетерогенных реакций с участием газообразных веществ. Для выяснения зависимости константы равновесия от давления используется константа равновесия, выраженная через мольные доли компонентов К х (К р и К с от давления не зависят).









