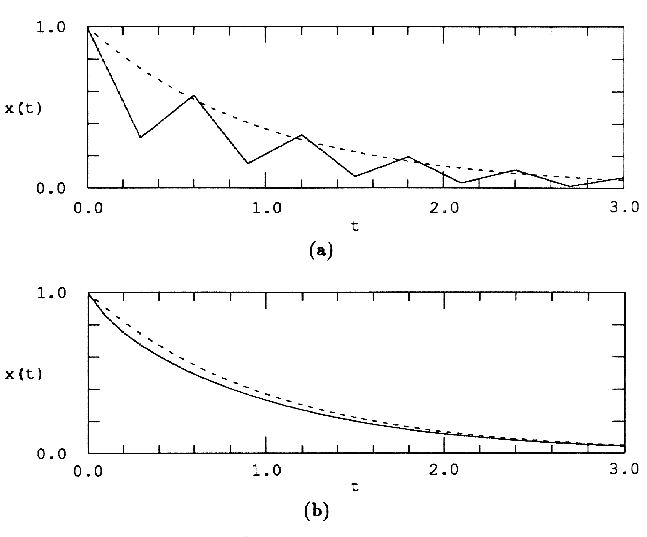
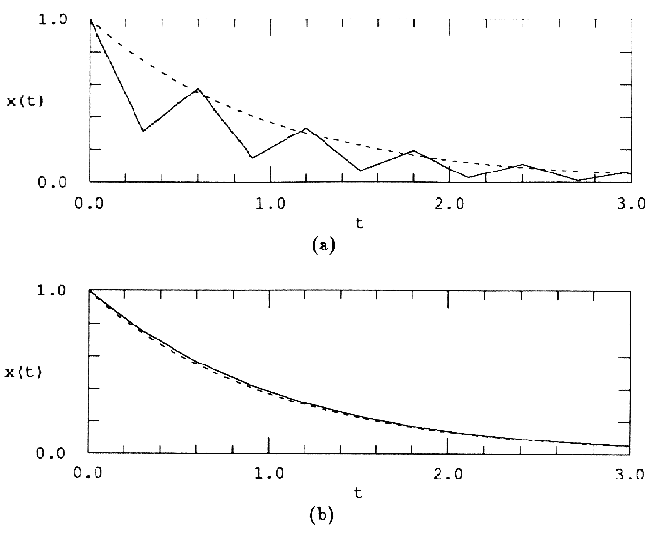
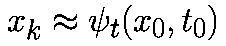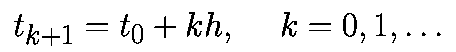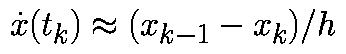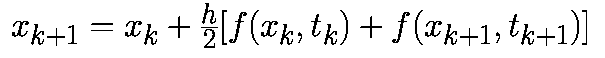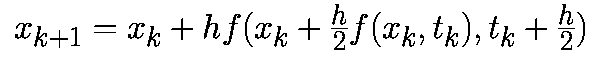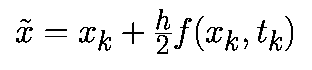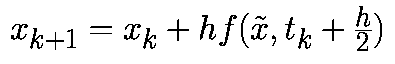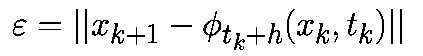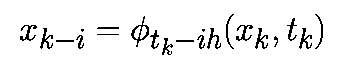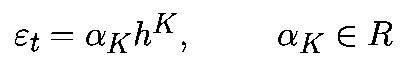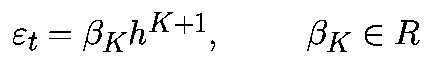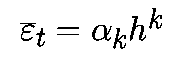Системой дифференциальных уравнений называется система вида
где x — независимый аргумент,
yi — зависимая функция, 
Функции yi(x), при подстановке которой система уравнений обращается в тождество, называется решением системой дифференциальных уравнений.
Численные методы решения систем дифференциальных уравнений.
Модифицированный метод Эйлера.
Метод Рунге-Кутта четвертого порядка.
Дифференциальным уравнением второго порядка называется уравнение вида
| F(x,y,у’,y»)=0 | (1) |
| y»=f(x,y,y’). | (2) |
Функция y(x), при подстановке которой уравнение обращается в тождество, называется решением дифференциального уравнения.
Численно ищется частное решение уравнения (2), которое удовлетворяет заданным начальным условиям, то есть решается задача Коши.
Для численного решения дифференциальное уравнение второго порядка преобразуется в систему двух дифференциальных уравнений первого порядка и приводится к машинному виду (3). Для этого вводится новая неизвестная функция 
 . . | (3) |
Функция f2(x, y1, y) в систему (3) введена формально для того, чтобы методы, которые будут показаны ниже, могли быть использованы для решения произвольной системы дифференциальных уравнений первого порядка. Рассмотрим несколько численных методов решения системы (3). Расчетные зависимости для i+1 шага интегрирования имеют следующий вид. Для решения системы из n уравнений расчетные формулы приведены выше. Для решения системы из двух уравнений расчетные формулы удобно записать без двойных индексов в следующем виде:
Метод Рунге-Кутта четвертого порядка.
где h — шаг интегрирования. Начальные условия при численном интегрировании учитываются на нулевом шаге: i=0, x=x0, y1=y10, y=y0.
Контрольное задание по зачетной работе.
Колебания с одной степенью свободы
Цель. Изучение численных методов решения дифференциальных уравнений второго порядка и систем дифференциальных уравнений первого порядка.
Задание. Численно и аналитически найти:
- закон движения материальной точки на пружинке х(t),
- закон изменения силы тока I(t) в колебательном контуре (RLC — цепи) для заданных в табл.1,2 режимов. Построить графики искомых функций.
Свободные незатухающие колебания
Затухающее колебательное движение
Предельное апериодическое движение
Вынужденное колебание без сопротивления
Вынужденное колебание без сопротивления, явление резонанса
Вынужденное колебание с линейным сопротивлением
Вынужденное колебание с линейным сопротивлением, явление резонанса
Видео:Метод ЭйлераСкачать

Интегрирование системы дифференциальных уравнений методом эйлера
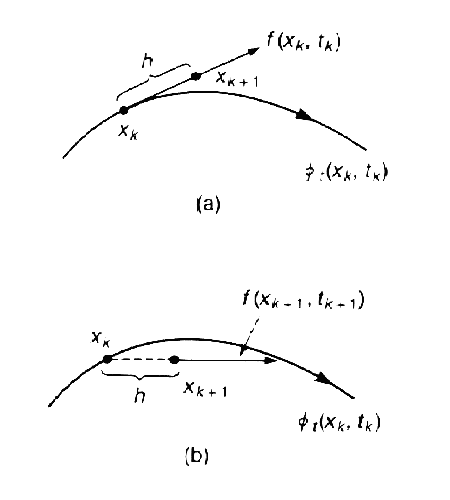
последовательностью точек x0,x1. в соответствующие моменты времени t0,t1. Значения точек должны удоволетворять приближенному равенству
Если специально не оговорено иное, то предполагается, что моменты времени выбираются через равные интервалы с величиной шага h>0, то есть
Аппроксимируем производную в момент времени tk соотношением
При такой аппроксимации уравнение (1) примет вид:
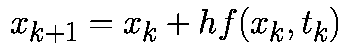 |
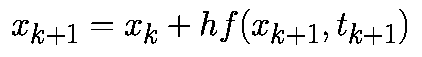 |
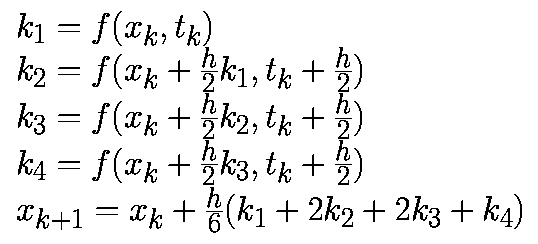 |
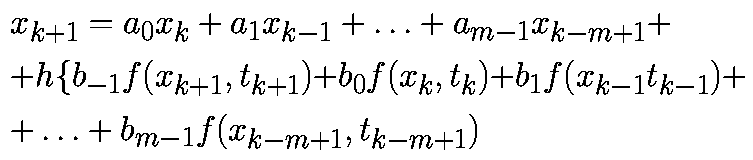 |
| Время, с | Скорость, м/с |
| 0.0 | 0.0 |
| 0.1 | -1.0 |
| 0.2 | -2.0 |
| 0.3 | -3.0 |
| 0.4 | -4.0 |
| 0.5 | -5.0 |
| 0.6 | -6.0 |
| 0.7 | -7.0 |
| 0.8 | -8.0 |
| 0.9 | -9.0 |
| 1.0 | -10.0 |
То есть, воспользовавшись формулой
мы получили зависимость скорости точки от времени. А всего-то нужно взять значение скорости в текущий момент времени, и добавить к нему приращение, которое скорость получит в новый момент времени, отстоящий от текущего на секунд. Приращение времени называется здесь шагом интегрирования. А приращение мы вычисляем как значение производной искомой функции в текущий момент времени умноженное на шаг. Просто? Да просто конечно. И та формула, которую я написал, имеет название название — явный метод Эйлера для численного решения дифференциальных уравнений. Это так называемая рекуррентная формула, когда новое значение вычисляемой величины зависит от её предыдущего значения.
А что же с высотой точки над Землей? Да всё аналогично, смотрите
ведь проекция скорости есть производная от соответствующей координаты. Применим формулу метода Эйлера для этого уравнения, ведь скорость мы уже знаем
и по этой формуле добавим в нашу таблицу ещё одну колонку
| Время, с | Скорость, м/с | Высота, м |
| 0.0 | 0.0 | 100.0 |
| 0.1 | -1.0 | 100.0 |
| 0.2 | -2.0 | 99.9 |
| 0.3 | -3.0 | 99.7 |
| 0.4 | -4.0 | 99.4 |
| 0.5 | -5.0 | 99.0 |
| 0.6 | -6.0 | 98.5 |
| 0.7 | -7.0 | 97.9 |
| 0.8 | -8.0 | 97.2 |
| 0.9 | -9.0 | 96.4 |
| 1.0 | -10.0 | 95.5 |
Хм, ну, во-первых, заметно, что высота меняется у нас уже неравномерно, так как скорость со временем меняется. Теперь наша производная сама зависит от времени. Но уже на первом шаге, мы замечаем неладное — скорость уже есть, а вот высота по прежнему 100 метров. Как так?
Это вышло потому, что на каждом шаге мы полагаем производную (скорость) постоянной. Метод не дает информации о том, что происходит с решением между шагами. Соответственно накапливается погрешность, сравним полученное решение с точным
| Время, с | Скорость, м/с | Высота, м | Точное решение, м |
| 0.0 | 0.0 | 100.0 | 100.00 |
| 0.1 | -1.0 | 100.0 | 99.95 |
| 0.2 | -2.0 | 99.9 | 99.80 |
| 0.3 | -3.0 | 99.7 | 99.55 |
| 0.4 | -4.0 | 99.4 | 99.20 |
| 0.5 | -5.0 | 99.0 | 98.75 |
| 0.6 | -6.0 | 98.5 | 98.20 |
| 0.7 | -7.0 | 97.9 | 97.55 |
| 0.8 | -8.0 | 97.2 | 96.80 |
| 0.9 | -9.0 | 96.4 | 95.95 |
| 1.0 | -10.0 | 95.5 | 95.00 |
Да, наш камень как будто зависает в воздухе. Численное решение отстает от аналитического, и чем дальше мы считаем, тем выше погрешность счета. Погрешность накапливается, так как на каждом шаге мы берем всё более и более грубое приближение. Что делать?
Во первых, можно уменьшить шаг. Скажем в 10 раз, пусть секунды
| Время, с | Скорость, м/с | Высота, м | Точное решение, м |
| 0.0 | 0.0 | 100.0 | 100.00 |
| 0.1 | -1.0 | 99.96 | 99.95 |
| 0.2 | -2.0 | 99.81 | 99.80 |
| 0.3 | -3.0 | 99.57 | 99.55 |
| 0.4 | -4.0 | 99.22 | 99.20 |
| 0.5 | -5.0 | 98.78 | 98.75 |
| 0.6 | -6.0 | 98.23 | 98.20 |
| 0.7 | -7.0 | 97.59 | 97.55 |
| 0.8 | -8.0 | 96.84 | 96.80 |
| 0.9 | -9.0 | 96.00 | 95.95 |
| 1.0 | -10.0 | 95.05 | 95.00 |
Уже лучше, погрешность в конце счета не превышает 0,05 метров, и это в 10 раз меньше предыдущего значения. Можно предположить, что уменьшив шаг ещё в 10 раз мы получим ещё более точное решение. Я схитрил, выводя значения только для 10 точек с шагом 0.1, на самом деле, чтобы получить такую таблицу нужны уже 100 итерации а не 10. При шаге 0.001 потребуется уже тысяча итераций, а результат будет таким
| Время, с | Скорость, м/с | Высота, м | Точное решение, м |
| 0.0 | 0.0 | 100.0 | 100.00 |
| 0.1 | -1.0 | 99.9505 | 99.95 |
| 0.2 | -2.0 | 99.8010 | 99.80 |
| 0.3 | -3.0 | 99.5515 | 99.55 |
| 0.4 | -4.0 | 99.2020 | 99.20 |
| 0.5 | -5.0 | 98.7525 | 98.75 |
| 0.6 | -6.0 | 98.2030 | 98.20 |
| 0.7 | -7.0 | 97.5535 | 97.55 |
| 0.8 | -8.0 | 96.8040 | 96.80 |
| 0.9 | -9.0 | 95.9545 | 95.95 |
| 1.0 | -10.0 | 95.0050 | 95.00 |
Если вы попробовали выполнить эти расчеты в ручную, то понимаете теперь насколько они однообразны и трудоемки, если нужна высокая точность. Именно поэтому расцвет численного моделирования совпал с появлением компьютеров. Они как раз и нужны для того, чтобы быстро выполнять множество однообразных операций над числами.
Метод Эйлера самый простой из известных методов интегрирования дифференциальных уравнений. Из нашего простого примера видно, что погрешность метода прямо пропорциональна шагу интегрирования, и это действительно так. Такие методы называются методами 1-го порядка точности.
Точность расчетов даже на шаге 0.1 можно улучшить, если мы применим, скажем метод Рунге-Кутты 4-го порядка точности. Но это отдельная история.
Видео:Численное интегрирование методом ЭйлераСкачать

Заключение
Задумайтесь… Мы рассмотрели очень простой пример. Мы даже не применяли компьютер, но уже понимаем принцип, по которому работают те самые мощные в мире суперкомпьютеры, что моделируют ранние этапы жизни Вселенной. Конечно, там всё устроено гораздо сложнее, но принцип лежит этот же самый.
Представьте себе, какой мощный инструмент вы получаете в свои руки. Эта последняя статья, где мы не будем применять компьютер. Я обещал Octave. В следующий раз будет именно он.
🔥 Видео
Видеоурок "Системы дифференциальных уравнений"Скачать

Видеоурок "Системы диф. уравнений. Метод Эйлера"Скачать

Метод Эйлера. Решение систем ДУСкачать

Дифференциальное уравнение. Формула ЭйлераСкачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Системы дифференциальных уравненийСкачать

Системы дифференциальных уравнений.Метод исключения.Метод Эйлера.Скачать

Численное решение задачи Коши методом ЭйлераСкачать

Численное решение системы дифференциальных уравнений(задачи Коши)Скачать

5 Численное решение дифференциальных уравнений Part 1Скачать

Линейные системы дифференциальных уравнений с постоянными коэффициентамиСкачать

МЗЭ 2022 Численное решение дифференциальных уравнений Метод Эйлера Ложкин С. А.Скачать

Системы дифференциальных уравненийСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать