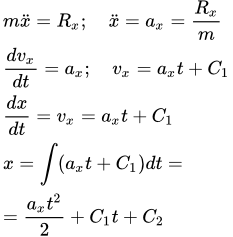Интегрирование дифференциальных уравнений движения материальной точки в случае p const

Видео:Дифференциальные уравнения движения точкиСкачать

Метод решения задач

Дифференциальные уравнения движения точки

Здесь мы рассмотрим движение материальной точки под действием постоянных сил. Пусть на точку массой m действуют n сил , которые постоянны на протяжении всего движения точки. Тогда удобно использовать равнодействующую , равную их векторной сумме:
.
Выберем инерциальную декартову систему координат Oxyz с началом в некоторой точке O . Закон движения точки в ней определяется вторым законом Ньютона:
(1) .
Здесь – радиус-вектор точки. То есть вектор, приведенный из начала координат O к материальной точке.

Проектируя векторное уравнение (1) на оси системы координат, получим систему дифференциальных уравнений, описывающих движение точки:
(2) .

Решение дифференциальных уравнений при действии постоянных сил

Если силы постоянны, то и их векторная сумма также постоянна. В этом случае уравнения (2) не зависят друг от друга. Поэтому каждое из этих уравнений можно решать отдельно от остальных. Рассмотрим уравнение для координаты x :
(3) .
Найдем его решение.

Разделим уравнение (3) на m и введем обозначение:
.
Тогда уравнение (3) примет более простой вид:
(4) .
Введенная нами величина является проекцией ускорения точки на ось x . В рассматриваемом нами случае постоянных сил, ускорение также постоянно.

Вторая производная координаты x по времени – это производная проекции скорости на ось x по времени. При этом применяют следующие обозначения:
(5) .
Проекция скорости на ось x – это производная координаты по времени:
(6) .

Найдем закон изменения со временем проекции скорости материальной точки на ось x : . Подставим (5) в (4):
.
Это простое дифференциальное уравнение с разделяющимися переменными. Перепишем его в следующем виде:
.
Интегрируем, используя таблицу неопределенных интегралов.
.
Здесь – постоянная интегрирования, которая определяется из начальных условий. Поскольку тоже постоянная, то, чтобы придать решению более простой вид, заменим на . В результате получим закон изменения проекции скорости на ось x :
(7) .
Как видно, скорость является линейной функцией от времени. Тот факт, что зависит от времени, можно записать так:
.

Зная значение в определенный момент времени, можно определить значение постоянной . Пусть, например, нам известно, что в начальный момент времени , проекция скорости на ось x равняется . Подставим в (7) :
.
Отсюда . Тогда закон изменения проекции скорости на ось x имеет определенный вид:
.

Теперь найдем закон изменения координаты точки x от времени: . Из (6) и (7) имеем:
;
.
Это также дифференциальное уравнение с разделяющимися переменными. Интегрируем с помощью таблицы интегралов.

.
Итак, мы получили закон изменения координаты от времени:
(8) .
Здесь – постоянные интегрирования. Их можно найти, зная скорость и координату, в какой-либо момент времени.

Пусть, например, в начальный момент времени , координата равна , и проекция скорости точки на ось x равна . Ранее мы уже нашли значение постоянной для этого случая: . Подставим в (8):
.
Подставим сюда :
.
Отсюда .
Тем самым мы получили закон изменения x координаты от времени:
.

Уравнения движения (2) для остальных переменных y и z , при постоянных силах, решаются точно так же, как и для переменной x . Далее мы приводим пример решения задачи на интегрирование дифференциальных уравнений движения материальной точки при действии на нее постоянных сил.

Видео:Дифференциальные уравнения движения материальной точкиСкачать

Задача

Условие задачи

Груз S, рассматриваемый как материальная точка массы m = 5кг, движется по шероховатой поверхности от точки A до точки B, в которой отрывается от поверхности и продолжает движение в воздухе до падения на наклонную поверхность в точке C. Движение происходит в плоскости рисунка.

В точке A, груз имел скорость м/с. Скорость в точке B: м/с. Участок AB представляет собой плоскую поверхность с углом наклона α = 30° к горизонту. На участке AB, кроме силы тяжести и силы трения, на груз действует постоянная сила Н, направленная под углом φ = 45° к поверхности. Коэффициент трения f = 0,1 .

На участке BC, груз движется под действием только силы тяжести. Сопротивлением воздуха пренебречь. Поверхность, на которую падает груз, является плоской с углом наклона β = 15° к горизонту (см. рисунок). Точка D расположена ниже точки B на расстояние |BD| = h = 1 м .

Найти: Время движения на участке AB; длину этого участка; время падения от точки B к точке C; расстояние |DC|; уравнение траектории BC.

Решение задачи

1. Движение материальной точки на участке AB

1.1. Составление уравнения движения и определение ускорения

Рассмотрим движение груза S на участке AB. Как сказано в условии, его можно рассматривать как материальную точку. То есть считаем, что размерами груза можно пренебречь.

Выберем декартову систему координат с началом в точке A. Ось x направим от A к B; ось y – перпендикулярно. Пусть в начальный момент времени , груз находился в точке A.

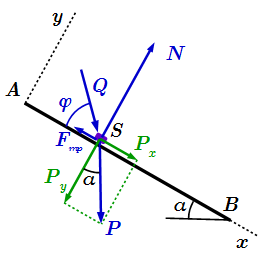
Силы, действующие на груз S на участке AB.

Рассмотрим силы, действующие на груз, и найдем их компоненты в выбранной системе координат Axy .
1) Сила тяжести , где м/с 2 – ускорение свободного падения. Она направлена вертикально вниз. Разложим ее на составляющие вдоль координатных осей по правилу параллелограмма: (см. рисунок). Поскольку вектор перпендикулярен горизонтали, а вектор перпендикулярен поверхности AB, то угол между векторами и равен углу между горизонталью и поверхностью движения, который по условию равен α . Тогда сила тяжести имеет следующие проекции на оси выбранной системы координат:
.
2) Заданная сила . По условию, она направлена под углом φ к поверхности (см. рисунок). Находим ее компоненты в системе координат Axy :
.
3) Сила давления поверхности . Она перпендикулярна поверхности. Поэтому ее компоненты:
.
4) Сила трения . Она направлена противоположно перемещению, то есть противоположно оси x . Абсолютная величина силы трения определяется по закону Амонта – Кулона:
(AB.1) .
Ее компоненты:
.

Составляем дифференциальные уравнения движения материальной точки:
.
Здесь мы учли, что движение происходит в плоскости xy . Поэтому уравнение для z компоненты тождественно обращается в нуль. Подставляем перечисленные выше компоненты внешних сил.
(AB.2) ;
(AB.3) .

Перемещение вдоль оси y отсутствует. Это означает, что координата y точки S остается постоянной при движении на участке AB. Тогда и все ее производные по времени равны нулю. Поэтому . Тогда из (AB.3) и (AB.1) имеем:
;
.

Разделим (AB.2) на m . В результате получим дифференциальное уравнение движения точки в следующем виде:
.
Вторая производная координаты по времени есть ускорение точки. Обозначим его как . Поскольку все действующие внешние силы постоянны, то ускорение постоянно.

.
В результате уравнение движения точки примет более простой вид:
(AB.4) ,
где – ускорение точки, постоянная величина.

1.2. Интегрирование уравнений движения

Итак, мы составили дифференциальное уравнение движения материальной точки S на участке AB:
(AB.4) ,
Теперь переходим к интегрированию этого уравнения.

Разберемся с обозначениями. У нас x – это координата точки, определяющая ее положение. Скорость точки – это производная координаты по времени t :
(AB.5) .
При , точка движется в сторону возрастания координаты x : от A к B. При – в противоположную сторону.
Ускорение – это производная скорости по времени, или вторая производная координаты по времени:
.

Определяем закон изменения скорости со временем. Для этого выразим уравнение (AB.4) через скорость :
.
Это простейшее дифференциальное уравнение с разделяющимися переменными. Интегрируем его, учитывая, что – это постоянная Для этого используем таблицу неопределенных интегралов.
;
;
(AB.6) .
Здесь – постоянная интегрирования. Найдем ее значение из условия, что в начальный момент времени , груз S находился в точке A и имел скорость в направлении оси x . Подставляем в (AB.6) , :
.
Отсюда . Тогда закон изменения скорости со временем принимает следующий вид:
(AB.7) .

Определяем время движения груза на участке AB. Для удобства, обозначим моменты времени, в которых груз находился в точках A и B, как и . Поскольку, по принятому нами соглашению, , то . Подставим в (AB.7) значения для точки B: . Тогда
. Отсюда
.

Теперь найдем зависимость координаты груза x от времени. Для этого воспользуемся тем, что скорость есть производная координаты по времени (см. (AB.5)):
.
Зависимость мы уже нашли: . Подставляем и интегрируем.
;
;

;
.
Здесь – постоянная интегрирования. Найдем ее из условия, что в начальный момент времени, , груз находился в точке A, в которой . Подставляем , :
.
Отсюда .
Тем самым мы нашли закон движения точки S на участке AB:
(AB.8) .

Определяем длину участка AB. Нам известно, что в момент времени , груз находился в точке A. В момент времени – в точке B. Также нам известен закон движения точки . Это позволяет найти длину участка AB:

.

1.3. Проверка решения

Сделаем проверку. Для этого воспользуемся теоремой об изменении кинетической энергии точки. Согласно этой теореме, Изменение кинетической энергии материальной точки, при переходе из точки A в точку B, равно сумме работ всех сил, приложенных к точке на этом перемещении:
(AB.9) .

Находим сумму проекций всех сил на ось x , приложенных к грузу на участке AB:

.
Находим сумму работ всех внешних сил, произведенных при перемещении груза из точки A в точку B.
.

Находим разность кинетических энергий груза при перемещении из точки A в точку B.
.

Подставим найденные значения в (AB.9):
.
Видно, что это уравнение выполняется. Различие имеется только в последней цифре. Это связано с округлениями, производимыми при вычислениях. Значит, этот этап решения выполнен верно.

2. Движение материальной точки на участке BC

2.1. Уравнения движения и их решения

Теперь рассмотрим движение груза S на участке BC. На этом участке мы выберем новую систему координат, и новый отсчет времени. Возьмем декартову систему координат с началом в точке B. Ось Bx направим по горизонтали; ось By – вертикально вверх (см. рисунок).

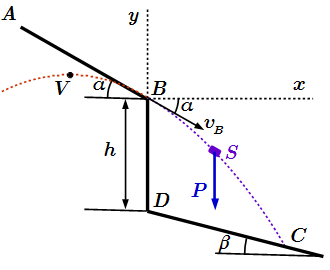
Движение груза на участке BC.

Началом движения, на участке BC, является точка B. Новый отсчет времени также будем производить от этой точки. Тогда в начальный момент времени , координаты груза равны нулю:
.
Нам известна скорость груза в точке B. Она имеет абсолютное значение , заданное в условии, и направлена вдоль прямой AB. И поэтому составляет угол α с горизонтальной осью Bx. Проекции скорости на оси координат равны:
.

На груз действует только одна сила тяжести , направленная вниз. Ее абсолютное значение . Выпишем ее компоненты в рассматриваемой системе координат (проекции силы тяжести на оси x и y):
.

Составляем уравнения движения.
.
Или
.
Разделим на m :
(BC1) ;
(BC2) .

Решаем первое уравнение (BC1). Сначала найдем закон изменения проекции скорости на ось x . Для этого, как и выше, используем следующие обозначения:
.
Выразим вторую производную в уравнении (BC1) через проекцию скорости на ось x :
;
.
Интегрируем это уравнение.
;
.
Здесь – постоянная интегрирования. Получилось, что проекция скорости груза на ось x не зависит от времени. Она постоянна для всех точек на участке BC. Поскольку нам известно значение в точке B, то . Тогда
(BC3) .
Теперь находим закон изменения координаты x от времени. Для этого воспользуемся тем, что . Подставляем в (BC3) и интегрируем.
;
;
.
Определяем постоянную интегрирования из начальных условий. В точке B . Подставляем :
.
Отсюда , и мы получаем закон изменения координаты x от времени:
(BC4) .

Аналогичным образом решаем второе уравнение:
(BC2) .
Находим закон изменения проекции скорости от времени. Используем следующие обозначения для проекции ускорения на ось y :
.
Выразим уравнение (BC2) через :
;
.
Интегрируем.
;
.
Находим значение постоянной интегрирования из начальных условий. При . Подставляем :
.
Отсюда . Так мы получили закон изменения проекции скорости на ось y :
(BC5) .
Находим закон изменения координаты y от времени. Подставляем в (BC5) и интегрируем.
;
;
.
Определяем постоянную интегрирования из начальных условий. В точке B . Подставляем :
.
Отсюда . И мы получаем закон изменения координаты y от времени:
(BC6) .

2.2. Определение координат точки C

Итак, мы получили закон движения материальной точки S в виде двух уравнений.
(BC4) ;
(BC6) .
Найдем положение точки C.

Для этого нам нужно найти уравнение прямой DC. В общем виде, уравнение прямой описывается по формуле:
(BC7) .
Здесь k – это угловой коэффициент, равный тангенсу угла наклона прямой к оси x . Положительным считается направление поворота от оси x против часовой стрелки. В нашем случае угол наклона отрицательный и равен . Поэтому
.
Найдем значение коэффициента b . Воспользуемся тем, что нам известны координаты точки D, принадлежащие прямой:
.
Подставим в (BC7):
;
.
Отсюда .
Таким образом, мы нашли уравнение прямой DC:
(BC8) ,
где .

Теперь найдем координаты точки C. Для этого нам нужно найти точку пересечения кривой, заданной уравнениями (BC4)–(BC6) и прямой (BC8). Координаты точки C удовлетворяют всем этим уравнениям:
(BC4) ;
(BC6) ;
(BC8) .
Решаем систему трех уравнений (BC4), (BC6) и (BC8). Подставляем (BC4) и (BC6) в (BC8) и выполняем преобразования:
;
.
Решаем квадратное уравнение. Подставляем численные значения.
;

;
;
.
Получаем корни уравнения:
.
Положительный корень дает момент времени, в который груз оказался в точке C . Это время движения по участку BC:
.

Находим значения координат точки C. Подставим найденное значение в (BC4):
.
Значение можно получить или из уравнения (BC6), или из (BC8). Поскольку последнее проще, то используем его:
.
Расстояние между точками D и C:
.

2.3. Траектория движения точки

Выше мы получили закон движения материальной точки S в виде двух уравнений.
(BC4) ;
(BC6) .
Теперь найдем уравнение ее траектории. Для этого мы должны исключить t из уравнений (BC4) и (BC6).

Из уравнения (BC4) находим:
.
Подставляем в (BC6) и выполняем преобразования.
;

;
;
.
Это уравнение параболы. Ее вершина V находится в точке с координатами
;
.
Фокальный параметр:
.
С этими обозначениями, уравнение параболы можно записать в каноническом виде:
.

.
Траектория движения груза на участке BC представляет собой параболу

с вершиной в точке V с координатами ,
и фокальным параметром .

Автор: Олег Одинцов . Опубликовано: 13-09-2020

Видео:Д1 Дифференциальные уравнения движения материальной точкиСкачать

ЧАСТНЫЕ СЛУЧАИ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ. КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ

Рассмотрим прямолинейное движение свободной точки. При этом скорость и ускорение точки направлены вдоль прямой движения (обозначим ее Ох) и, следовательно, сила, действующая на точку, тоже направлена вдоль этой прямой:

Это ДУ второго порядка и является дифференциальным уравнением прямолинейного движения точки. Часто его можно заменить эквивалентной системой из двух ДУ первого порядка:

В общем случае действующая активная сила является функцией от времени, положения и скорости точки X=X(t, х, v_x). Рассмотрим частные случаи, когда сила является постоянной Х= const или зависящей только от одного из параметров: времени X=X(t); положения точки X = Х(х); скорости точки X = X(v_x):

1) при Х= const (например, при движении в поле тяжести на небольших высотах X = mg) уравнение (2.1) используется в виде

, откуда имеем , и это уравнение интегрируем

2) при X = X(t) используется аналогичный порядок действий:

3) при X = Дх) (например, сила упругости пружины X = —сх)

переходят от дифференциала по времени к дифференциалу по координате с помощью формулы Таким образом, из

получают , откуда имеем , и это

уравнение интегрируется

4) при X = X<v_x) (например, силы сопротивления среды: разреженной X = — kv_x или более плотной X = —kv, 2 ) используем следующий порядок: , откуда и интегрируем

Пример 1 (свободное падение тела без учета сопротивления воздуха (сила постоянна)). Пренебрегая размерами тела, будем считать его материальной точкой. Направим ось Оу по траектории прямолинейного движения тела в сторону его движения и примем за начало координат начальное положение тела (рис. 2.1). Если начальная скорость тела равна нулю, то н. у. данного движения имеют вид: t = 0, у₀ = 0, у₀ = 0.

Рис. 2.1. К примеру 1: движение под действием постоянной силы

ДУ этого движения примет вид: ту = mg, откуда у =g, т.е. ускорение движения постоянно. Интегрируем это уравнение дважды и получаем:

Постоянные интегрирования найдем

по н. у. При подстановке в первое уравнение значений / = 0, у₀ =0 получим С, = 0; при подстановке во второе уравнение значений t — 0, у₀ — 0 получим С₂ = 0. Таким образом, уравнения свободного падения тела в пустоте примут вид:

Пример 2 (движение тела, брошенного под углом к горизонту (сила постоянна)). Совместим начало координат с точкой вылета тела, брошенного под углом а к горизонту с начальной скоростью v₀ (рис. 2.2). Тогда получим н. у. движения: / = 0, х₀ = 0, у₀ = 0, х₀ = v₀cos а, у₀ = v₀ sin а.

Рис. 2.2. К примеру 2: движение точки в поле силы тяжести Земли

Составим ДУ движения тела тх =0, ту = —mg. Откуда проекции ускорения равны х = 0 и у = —g. Сначала проинтегрируем дважды ДУ вдоль оси Ох: х = С,х= C_xt + С₂. Определим постоянные интегрирования.

Подставив в первое уравнение значение х₀ = v₀cosa, получим С, = v₀ cos а. При подстановке во второе уравнение значений t = 0, х₀ = 0 получим С₂ = 0.

Проинтегрируем дважды по t ДУ

Из н. у. определим постоянные интегрирования: С₃ = v₀sin а и С₄ = 0. Окончательно имеем:

Проанализируем решение. Исключив время из уравнений движения (2.36 и 2.3в), получим уравнение траектории — параболы с вертикальной осью, ветвями, направленными вниз и вершиной в наивысшей точке. Определим модуль скорости движения как функцию

времени Эта формула показывает, что движение, полученное сложением равномерного горизонтального и равнопеременного вертикального движения, не является равнопеременным. Определим дальность и продолжительность полета тела. В точке падения тела на землю у — 0, и, подставляя это значение в уравнение (2.3в), получим два значения времени: момент вылета / = 0 и момент падения Дальность полета определим, подставив момент падения в уравнение (2.36): Наибольшую высоту

подъема тела можно определить из условия, что в наивысшей точке проекция скорости на вертикальную ось: у равна нулю. Подставляя это значение в уравнение (2.3а), получим время подъема:

Из уравнения (2.3в) получим высоту полета в этот момент времени:

Пример 3 (падение тела с учетом сопротивления воздуха (сила зависит только от скорости точки)). В условиях примера (2.1) рассмотрим падение тела при сопротивлении воздуха, пропорциональном скорости движения тела (см. далее рис. 2.3). Тогда силу сопротивления можно представить в виде F_conp = bv, где b — коэффициент пропорциональности. Обозначим к = b/т — коэффициент, который равен модулю силы сопротивления, приходящейся на единицу массы движущегося тела, при скорости его, равной единице, и имеет размерность с -1 .

Рис. 2.3. К примеру 3: движение под действием силы, зависящей от скорости

Составим ДУ движения тела ту = —mg — mkv, откуда у = —g — kv. Понизим порядок уравнения, перейдя от переменной у к переменной

v= у (т.е. от ДУ вида (2.1) перейдем к системе ДУ (2.1а)). Тогда и или, разделяя переменные, Введем переменную

Заменив переменную, получим

Интегрируя последнее уравнение, найдем In и = —kt + С,, т.е. ln(g — — kv) = —kt + С,.

Определим постоянную интегрирования, подставляя н. у. /= 0, у_п = О, С| = lng. Таким образом, имеем ln(g — kv) = —kt + lng, или

или, потенцируя, . Из этого уравнения получаем окончательно уравнение скорости:

При / —> °° имеем т.е. скорость падения все время

возрастает, стремясь к предельному значению Практически по истечении некоторого промежутка времени движение становится равномерны м.

Проинтегрируем (2.4). Так как и из него

следует: Подставляя н. у. t = 0, у_<) = 0, получим постоянную интегрирования: При найденном значении С₂ получим

уравнение движения падающего в воздухе тела:

Пример 4 (сила зависит от положения точки). Материальная точка М массой т — 20 г отталкивается от некоторого центра О силой, обратно пропорциональной кубу расстояния ОМ. В начальный момент времени известны: расстояние ОМ = 5 см, скорость точки v₀ = 10 см • с -1 , направленная по прямой ОМ от центра, и сила отталкивания Р= 0,4 мН. Получить уравнение движения точки под действием силы отталкивания, а также определить скорость, приобретенную точкой на расстоянии 20 см от центра.

Решение. Центр отталкивания примем за начало координат. Установим н. у.: t = 0, х₀ = ОМ₀ = 5, х₀ =10. Модуль силы отталкивания равен

, где коэффициент пропорциональности можно определить из н. у. Р₀ = 0,4 мН = 40 дин, откуда имеем к — Р₀х1 — 40 гр • см • с -2 х х 125 см 3 = 5000 гр • см 4 • с” 2 . Составим ДУ движения откуда

. Исключим из уравнения переменную t путем преобразования, описанного в п. 3 — Тогда ДУ примет вид

и, разделив переменные, получим

При интегрировании уравнения воспользуемся определенными интегралами с переменным верхним пределом. При изменении скорости от v₀

до v координата меняется от х₀ до х. Тогда

Подставив значения, получим уравнение скорости:

Откуда имеем при х = 20 скорость v = ^10,46 см • с -1 . Чтобы получить уравнение движения точки проинтегрируем (2.5), представив его в виде

Разделив переменные, имеем

Интегрируем это уравнение с переменным верхним пределом: или или

Возведя в квадрат и преобразуя, получим уравнение движения точки:

Заметим, что в приведенных ранее примерах 1—3 применение определенных интегралов с переменными верхними и нижними пределами, соответствующими н. у. при интегрировании переменных, освободило бы от определения постоянных интегрирования по н. у. И, наоборот, в примере 4 можно было бы применять неопределенные интегралы, определяя постоянные интегрирования по н. у.

Среди механических движений особое место занимают движения, которые периодически повторяются — механические колебания, например колебания маятников, струн, мостов при прохождении транспорта, корабля, вибрация различных деталей машин и механизмов. Решение связанных с этими движениями задач основано на теории линейных и нелинейных колебаний. Далее речь будет идти о линейных колебаниях, описываемых ЛДУ с постоянными коэффициентами (в самом общем виде это уравнение вида к₂х + к_<х + к₀х = Ь). Рассмотрим прямолинейные колебания материальной точки, иллюстрирующие решение второй основной задачи динамики точки. В зависимости от наличия восстанавливающей силы jP_n0CCTaH, силы сопротивления F и внешней возмущающей силы / г _возмущ различают свободные/собственные, затухающие и вынужденные колебания. В табл. 2.1 приведены общие результаты исследования этих колебаний.

Видео:Дифференциальные уравнения движения материальной точки. Часть 1Скачать

iSopromat.ru

Для интегрирования дифференциальных уравнений движения материальной точки необходимо знать значение координат и скорости точки в какой-либо момент времени (обычно в начальный), поэтому эти значения называют начальными условиями.

Из теории дифференциальных уравнений известно, что при интегрировании уравнения второго порядка появляются две произвольных постоянных интегрирования.

Следовательно, при интегрировании системы (4) появятся шесть постоянных интегрирования. Таким образом, решение системы (4) будет иметь вид

В зависимости от постоянных интегрирования получается целый класс решений, удовлетворяющих системе уравнений (4).

Чтобы получить конкретное решение, необходимо определить постоянные интегрирования.

Для этого необходимо знать значение координат и скорости точки в какой-либо момент времени (обычно в начальный), поэтому эти значения называют начальными условиями.

Таким образом, решение (6) можно переписать в виде

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Динамика материальной точки в НИСО. Нелинейное дифференциальное уравнение движенияСкачать

Интегрирование уравнений движения

Задачи динамики частицы бывают двух типов. Первый — задано движение частицы, и нужно найти действующую силу. Здесь нет особых трудностей: по заданному движению находим ускорение, и второй закон Ньютона определяет силу. Второй — задана сила, действующая на частицу, и нужно определить движение частицы, т. е. в конечном итоге найти координаты как функции времени. Эти задачи гораздо сложнее, и их решение требует решения дифференциальных уравнений. Некоторые задачи такого рода будут рассмотрены ниже.

Второй закон Ньютона приводит к дифференциальным уравнениям вида

С математической точки зрения механика частицы сводится к теории дифференциальных уравнений второго порядка приведенного вида. Возникающие здесь проблемы могут быть весьма непростыми. Мы рассмотрим несколько сравнительно простых случаев, для которых имеются стандартные процедуры, всегда приводящие к успеху.

1) Движение частицы под действием силы, зависящей от времени.

Пусть F = F(t) — заданная функция времени. Второй закон Ньютона дает уравнение

Перепишем его в виде

Интегрируя это равенство (формально — приписывая знак интеграла слева и справа), получим

Величина, стоящая слева, — изменение импульса за время /, интеграл в правой части в принципе вычисляется (штрихи у переменной / — дань математической аккуратности, для отличия верхнего предела интегрирования от переменной интегрирования). Формула (2.134) определяет вектор скорости в любой момент времени.

Под интегралом в правой части стоит известная (из (2.134)) функция времени, интеграл берется, и формула (2.136) определяет положение частицы в любой момент времени.

Внимание! Написанные уравнения*— векторные. Умножая их скалярно на постоянные базисные векторы /, у, к и помня, что для

любого вектора i а = а_х, мы вместо каждого векторного уравнения получим три скалярных.

Задача 2.29. На частицу действует сила F(t) = F₀ sin со/. Как будет двигаться частица?

Решение. Формула (2.134) дает

Здесь v(0) — значение скорости при / = 0 (начальная скорость). Если в момент «включения» силы частица покоилась, эта скорость равна нулю. Полученный результат не очевиден. Действующая сила периодически меняет знак и величину, но скорость знака не меняет!

Далее, формула (2.136) дает

Здесь r(0) — положение частицы в начальный момент. Полученное решение довольно любопытно. Видим, что частица дрейфует с постоянной скоростью в направлении вектора V = v(0)+F₀/(ma), и на это движение накладывается гармоническое колебание с амплитудой А = F₀/(rmo 2 ).

На электрон в поле электромагнитной волны действует сила

F = еЁ₀sin wt. Посмотрим, как ведет себя электрон в поле обычной радиоволны с напряженностью поля Е= 0,1 В/м и частотой 1000 кГц. Для скорости дрейфа получим

Это достаточно большая скорость. Амплитуда колебаний будет А = 0,5 мм. Вокруг читателя «роится» огромное количество таких электронов в любой момент времени.

2) Движение частицы под действием сипы, зависящей от скорости. Одномерное движение.

Одномерное движение — это движение частицы по заданной траектории (пример — трамвай на рельсах).

Пусть частица движется по заданной кривой. Положение частицы на кривой задается длиной дуги s, отсчитываемой от некоторой точки. Второй закон Ньютона дает уравнение

где F — тангенциальная сила (см. формулу (2.43)). Будем считать, что F= F(v) — заданная функция скорости. Преобразуем уравнение (2.137):

Интегрируя это равенство, получим

Поскольку F(v) — известная функция, интеграл в левой части равенства (2.139) берется и дает некоторую функцию скорости /(v). Равенство /(v) = t/m неявно определяет скорость как функцию времени. Разрешая это равенство относительно v, найдем функцию v = v(/). Далее пишем

Формула (2.140) дает положение точки в любой момент времени, и проблема полностью решена (должно быть понятно, что если мы знаем положение частицы в любой момент времени, то можем ответить на все вопросы относительно движения частицы).

Задача 2.30. Мяч падает с высоты Н с нулевой начальной скоростью. Сила сопротивления со стороны воздуха пропорциональна скорости. Как будет двигаться мяч?

Решение. На мяч действует сила F — mg — av, второе слагаемое представляет силу сопротивления, величина а зависит от размеров мяча. Отсутствие начальной скорости гарантирует падение по вертикали (при отсутствии ветра), так что мы имеем дело с одномерным движением. Пусть ось х направлена вертикально вниз. Второй закон Ньютона дает уравнение

Это уравнение типа (2.137). Уравнение (2.139) дает

Интеграл берется (сводится к табличному), и мы получаем

Разрешая это равенство относительно скорости, получим

Видим, что скорость со временем растет и стремится к постоянному значению v_inax = mg/а, причем это значение достигается тем быстрее, чем больше а.

Для координаты х равенство (2.140) дает

Выражение получилось громоздкое, но смысл его простой: первое слагаемое в правой части соответствует движению с постоянной скоростью, а второе дает поправку, существенную для начального периода ускорения.

Это точное решение. Для того чтобы оценить влияние сопротивления на режим падения в начальной стадии, получим приближенное решение. Известно, что при малых х справедливо разложение

С помощью этой формулы для скорости получим

Видим, что начальное ускорение равно g, но оно убывает линейно по времени.

Падение капель дождя происходит по найденным формулам. Скорость капель у поверхности земли порядка нескольких метров в секунду (это ясно всякому, кто наблюдал дождь из окна движущегося автомобиля). Попробуем оценить величину а. Пусть капля диаметром 3 мм имеет скорость 5 м/с. Это дает для а величину 0,00014 кг/с. Время достижения максимальной скорости порядка т/а = v/g = 0,5 с. На рис. 2.3 показан график функции /(/) = 5(1 — ехр(-2/)), представляющей скорость падающей капли в первые 3 секунды падения. По вертикальной оси — скорость в м/с.

Коэффициент а пропорционален радиусу капли, а масса — кубу радиуса. Поэтому чем меньше капля, тем медленнее она падает. Капли тумана висят практически неподвижно.

3) Движение частицы под действием силы, зависящей от координаты. Одномерное движение.

Пусть в уравнении

где F— тангенциальная сила, сила зависит от координаты: F= F(s). Нам нужно решить уравнение

Мы можем, конечно, написать

но толку от этого не будет: хотя сила и зависит от времени через переменную s, эта зависимость неизвестна, поэтому интеграл в правой части не берется. Уравнение (2.145) решается с помощью следующего трюка. Умножим обе части этого уравнения на скорость V.

Левая часть полученного уравнения есть производная по времени

—, а правая часть может быть представлена в виде

Такое представление всегда возможно: функция W(s) есть просто первообразная функции F(s). Уравнение, таким образом, принимает вид

Равенство (2.146) утверждает, что величина, стоящая в скобках, не меняется со временем, т. е. постоянна. Обозначая эту постоянную буквой Е, получаем

Обратите внимание. Скорость частицы v со временем меняется, координата s также меняется, но конструкция (2.147) не меняется! Это, конечно, важный математический факт (математик скажет, что равенство (2.147) дает первый интеграл уравнения (2.145)), но это есть также важный физический факт.

Если сила зависит от координаты, имеет место закон сохранения механической энергии. Функция W (s) представляет потенциальную энергию частицы. (Полезно сравнить полученный результат с тем, что мы обсуждали в п. 2.2.5.)

Формула (2.147) определяет скорость как функцию координаты:

Далее можно найти координату как функцию времени s = s(f) так, как это было показано в п. 1.2.5.

Задача 2.31. Частица массой т подвешена на нити длиной /. Частицу отклонили на угол а₀ от вертикали и отпустили без начальной скорости (рис. 2.4). Как будет двигаться частица? (Такое устройство называется математическим маятником.)

Решение. При указанных условиях частица не выходит из вертикальной плоскости и ее траектория — дуга окружности радиусом / (считаем, что а cos у, или |s| 2

Известно, что при малых х cosjc « 1 — —. С учетом этого для малых отклонений формула (2.152) примет вид

Далее пишем ds/dt = v(s), ds/v(s) = dt и

(Нижний предел в интеграле соответствует начальному положению частицы.) Интеграл табличный, и окончательно имеем

Такое движение называется гармоническим колебанием. На рис. 2.5 приведен результат численного интегрирования уравнения для маятника при начальном отклонении на угол п/2 при значении

JgJI = 1. Для сравнения на этом же графике изображена функция cos / (пунктир), которая описывает колебание при малых отклонениях.

Величина со = называется угловой

частотой, время Т одного полного колебания называется периодом колебания. Поскольку период косинуса равен 2я, имеем

Результат (2.154) означает, что период малых колебаний не зависит от начального смещения от положения равновесия и равен

Для больших отклонений это не так. Из графика видно, что период увеличивается с ростом начального отклонения и соответственно формула (2.155) не имеет места.

Задача 2.32. В условиях задачи 2.26 найти зависимость координаты шайбы от времени, если движение начинается с нулевой скоростью.

Решение. Из уравнения (2.130) следует, что частица движется под действием силы, зависящей от координаты (неважно, что это — фиктивная сила, появившаяся потому, что мы описываем движение шайбы в неинерциальной системе отсчета; формально уравнение имеет вид второго закона Ньютона, и его решение подпадает под разобранный случай). Итак, F(x) = mo 2 x Этой силе соответствует потенциальная энергия

Закон сохранения энергии дает равенство

(Было учтено, что в начальный момент частица находится в точке с координатой х₀ и имеет нулевую скорость.) Отсюда для скорости получаем

Интеграл берется, и в результате получаем

Разрешая это равенство относительно х, окончательно находим

Для малых времен, разлагая экспоненту в ряд, получим что можно было ожидать.

В заключение этого пункта отметим, что распространение компьютеров резко снизило остроту проблем, связанных с решением дифференциальных уравнений. Во многих случаях гораздо проще и целесообразнее получить численное решение, нежели исхитряться в попытках получить аналитическое. В качестве примера предлагается следующая задача.

Задача 2.33. С Северного полюса вертикально вверх стартует ракета с первой космической скоростью. Как будет двигаться ракета?

Решение. При вертикальном старте с Северного полюса ракета движется по прямой, и мы имеем дело с одномерным движением под действием силы, зависящей от координаты. Однако попытка получить аналитическое решение по изложенной выше программе наталкивается на трудности (попробуйте ее провести). Получим численное решение. Здесь также есть свои тонкости.

Пусть г — расстояние от центра Земли, скорость ракеты будет v = dr/dt. Второй закон Ньютона дает уравнение

Учитывая, что GM = gR 2 , где R — радиус Земли (см. п. 2.2.6), равенство (2.160) перепишем в виде

При численном интегрировании удобно вводить безразмерные переменные. Одна появилась сама собой — положим у = r/R. Уравнение (2.161) примет вид

Если теперь положить gt 2 /R — х 2 , t = -jR/g ? х, окончательно получим

Здесь уже переменные у их безразмерные. Для скорости получим

8 км/с называется первой космической скоростью. Решение уравнения (2.162) при начальных условиях у(0) = 1, у'(0) = 1, чему соответствует старт с поверхности Земли с первой космической скоростью, приведено на рис. 2.6. Сплошная кривая дает расстояние г, пунктирная — скорость V. Значение этих функций находилось в 100 точках на интервале х е [0, 5].

Из графика видно, что высота подъема равна радиусу Земли (что можно было найти и аналитически, см. задачу 2.19), и достигается эта высота в момент времени

📹 Видео

РГР Д1 Обратная задача динамикиСкачать

Дифференциальное уравнение движения материальной точки.Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Теоретическая механика. Задание Д2 (часть 1) из сборника ЯблонскогоСкачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

Дифференциальные уравнения движенияСкачать

Лекция. Динамика точкиСкачать

Теоретическая механика. Задание Д1 (часть 1) из сборника ЯблонскогоСкачать

Динамика точки. Законы Галилея-НьютонаСкачать

Форш П. А. - Теоретическая механика - Интегрирование уравнений движения. Одномерное движениеСкачать

Динамика. Введение, дифференциальные уравнения движения точки, прямая и обратная задачи динамики.Скачать