Интегральное регулирование — это составная часть процесса регулирования, которая формирует регулирующее воздействие пропорционально интегралу отклонения регулируемой величины так долго, пока существует отклонение. Проще сказать, выходной сигнал регулятора будет воздействовать на регулирующий орган до тех пор, пока смещение не будет устранено и регулируемая переменная не вернется к заданному значению.

Входным сигналом интегрального регулятора является пневматический сигнал, который представляет уровень воды в резервуаре. Выход регулятора — пневматический сигнал, который перемещает регулирующий клапан (4), что приводит к изменению притока воды в резервуар.
В этом примере принимают, что постоянное возмущающее воздействие увеличивает приток воды в резервуар, что приводит к повышению уровня воды в резервуаре.
- Интегральный закон регулирования
- Принцип работы интегрального регулирования
- 4Курс_Автоматизац_Ч-1. Конспект лекций по дисциплине «Основы автоматизации горного производства» для специальности 090302 «Обогащение полезных ископаемых»
- Законы автоматического регулирования
- Законы автоматического регулирования
- 📽️ Видео
Видео:Непрерывные законы регулированияСкачать

Интегральный закон регулирования
Интегральный закон регулирования — это процесс регулирования, при котором регулирующее воздействие пропорционально интегралу по времени отклонения регулируемой величины, т.е. величине отклонения и времени этого отклонения, и, следовательно, производится так долго пока существует отклонение (изодромный — равнобегущий).
Видео:Что такое регуляторы, какие они бывают, как настраиваются, ПИД регуляторыСкачать

Принцип работы интегрального регулирования
Интегральное регулирование не существует непосредственно само по себе: оно всегда соединяется с пропорциональным регулированием. При пропорциональном регулировании выходной сигнал регулятора изменяется пропорционально изменению входного сигнала. Другими словами, если входной сигнал увеличится на некоторую величину, выходной сигнал регулятора также возрастет на пропорциональное этому изменению величину. Когда изменения на вводе прекращаются, вывод регулятора также перестает изменяться, что часто приводит к появлению неустранимого пропорциональным регулятором смещения регулируемой переменной от уставки. Когда в процесс регулирования к пропорциональной составляющей добавляется интегральная, регулятор продолжает корректировать вывод до полного возврата регулируемой переменной процесса к уставке. Интегральное регулирование, фактически, пропорциональное плюс интегральное регулирование добавляет корректирующее действие к пропорциональному действию.
Не смотря на то, что интегральное регулирование всегда используется в комбинации с пропорциональным регулированием, полезно исследовать характеристики интегрального регулирования, как будто бы процесс интегрального регулирования мог бы осуществляться непосредственно.
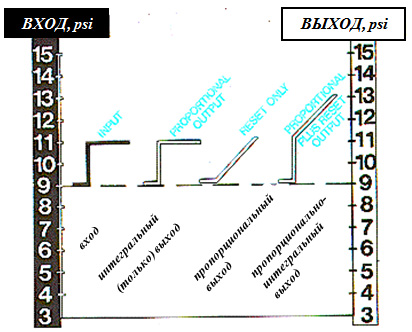
Обратите внимание, что интегральный выходной сигнал — это постепенно возрастающий сигнал. В этом как раз и проявляется основное свойство интегрального регулирования, которое преодолевает смещение и возвращает регулируемую переменную процесса к уставке.
Видео:О PID регуляторе простым языком (что такое ПИДы)Скачать

4Курс_Автоматизац_Ч-1. Конспект лекций по дисциплине «Основы автоматизации горного производства» для специальности 090302 «Обогащение полезных ископаемых»
| Название | Конспект лекций по дисциплине «Основы автоматизации горного производства» для специальности 090302 «Обогащение полезных ископаемых» |
| Анкор | 4Курс_Автоматизац_Ч-1.doc |
| Дата | 04.11.2017 |
| Размер | 4.02 Mb. |
| Формат файла |  |
| Имя файла | 4Курс_Автоматизац_Ч-1.doc |
| Тип | Конспект лекций #10121 |
| страница | 3 из 10 |
Автоматичекие регуляторы, переходные процессы, законы регулирования Понятие регулятора. Классификация по различным признакам. Представление о законах регулирования. Динамические характеристики регуляторов и их аналитическое и графическое представление. Структурные схемы регуляторов. Формирование законов регулирования Одним из основных элементов, входящим в систему регулирования является автоматический регулятор – устройство, изменяющее или стабилизирующее выходную величину объекта регулирования по заданному алгоритму путем воздействия на его входную величину. Классификация регуляторов может осуществляться по различным признакам. По способу действия они делятся на регуляторы прямого и непрямого действия. На практике более широкое применение получили регуляторы непрямого действия. Данные регуляторы классифицируются по виду источника подводимой энергии для перемещения исполнительного механизма: электрические, гидравлические, пневматические и комбинированные. Кроме того, регуляторы классифицируются на релейные, непрерывные и импульсные. Релейные регуляторы называют еще позиционными. Регуляторы подразделяются также на экстремальные и стабилизирующие. Экстремальные регуляторы могут использоваться на объектах, характеризующихся экстремальной статической характеристикой. Наибольшее распространение получили стабилизирующие регуляторы (рис. 5.1).
На схеме обозначено: μ – воздействие регулятора на регулирующий орган (РО) с помощью исполнительного механизма (ИМ); Δ – сигнал рассогласования, выделенный на элементе сравнения (ЭС) и равный векторной разнице между текущим (yт) и заданным (yз) значениями регулируемой величины Зависимость управляющего сигнала, вырабатываемого регулятором, от сигнала рассогласования во времени определяется законом регулирования, в общем виде эта зависимость может быть представлена: В зависимости от вида функции (5.1) стабилизирующие регуляторы классифицируются на интегральные (И), пропорциональные (П), пропорционально-интегральные (ПИ), пропорционально-дифферен—циальные (ПД) и пропорционально-интегрально-дифференциальные (ПИД). Закон регулирования формируется с помощью обратных связей. С учетом динамических свойств объекта управления он определяет вид и качество переходного процесса в АСР. В лекции рассмотрені подробно все законы регулирования и их динамические характеристики. Интегральный (И) закон регулирования. Регуляторы, реализующие данный закон, часто называют астатическими или регуляторами без обратной связи. В динамическом отношении И-закон регулирования подобен интегрирующему звену, уравнение регулятора и передаточная функция имеют вид:
или в дифференциальной форме:
где kр – статический коэффициент передачи регулятора; Из (5.2) следует, что скорость движения регулирующего органа для данного закона пропорциональна величине рассогласования. На рис. 5.2 а показана переходная функция И-регулятора. Регуляторы, работающие по данному закону, всегда приводят регулируемый параметр к заданному значению, если объект обладает свойством самовыравнивания (рис. 5.2 б, кривая 1). Применение данного закона регулирования при управлении астатическим объектом, приводит к переходному процессу в виде незатухающих колебаний выходного параметра (кривая 2, рис. 5.2). Пропорциональный (П) закон регулирования. Регуляторы, реализующие данный закон, еще называют регуляторами с жесткой обратной связью или статическими. Уравнение П-регулятора и передаточная функция имеют вид:
где (кр) — коэффициент передачи регулятора. . Переходная функция П-регулятора и типичный переходный процесс показаны на рис. 5.3. Из-за жесткой обратной связи П-регулятор не имеет возможности привести к заданному значению регулируемый параметр при изменении нагрузки на объект. Данное явление получило название остаточной неравномерности регулирования, она оценивается степенью неравномерности (δ), равной δ=1/кр.=Δ/μ.. Пропорциональные регуляторы обеспечивают устойчивую работу практически всех промышленных объектов. Пропорционально-дифференциальный (ПИ) закон регулирования. Регуляторы, работающие по данному закону, производят перемещение регулирующего органа пропорционально сумме отклонения и интеграла от отклонения регулируемой величины, т.е. осуществляют П- и И- воздействие:
или в дифференциальной форме:
Пропорционально-дифференциальный (ПД) закон регулирования. Регулятор, реализующий данный закон регулирования можно представить в виде системы, содержащей два параллельно работающих типовых звена: пропорционального и идеального дифференцирующего. Тогда уравнение ПД-закона имеет вид:
Пропорционально-интегрально-дифференциальный (ПИД) закон регулирования . Наиболее сложный алгоритм, включающий воздействие всех вышерассмотренных законов. Очевидно, что уравнение ПИД — закона имеют вид: Перейдя к операторной форме, получим передаточную функцию: На рис. 5.5 б представлена переходная функция ПИД-закона, где выделены области воздействия составляющими П, И и Д – закона. Формирование законов регулирования Раннее отмечалось, что закон регулирования определяется видом обратной связи или ее отсутствием На рис. 5.6 показаны варианты структурных схем регуляторов, отличающиеся способом формирования сигнала обратной связи. В лекции показана справедливость выражения:
которое позволяет определить передаточную функцию обратной связи (W(p)ос) для принятого закона регулирования.
Литература к теме: [5], [6] Качество регулирования. Выбор законов регулирования Понятие переходного процесса в АСР. Показатели качества переходного процесса – динамическое и остаточное отклонение,квадратичніе критерий качества, время регули-рования. Типовые переходные процессы. Динамический коєффициент регулирования.Выбор закона регулирования. Вид переходного процесса при регулировании определяет качество регулирования. Основными показателями качество регулирования являются следующие. Максимальное динамическое отклонение , представляет собой максимальную амплитуду отклонения выходного параметра (y1, рис. 5.7). Остаточное отклонение, характеризует величину отклонения регулируемой величины от заданного значения по окончании переходного процесса. Оценивается степенью неравномерности (δ). Время регулирования. Это период времени tр (рис. 6.1) от момента поступления на вход ступенчатого воздействия до момента, когда отклонение регулируемой величины от заданного значения становится меньше зоні нечувствительности регулятора. Квадратичный интегральный критерий качества. Характеризует суммарную площадь, ограниченную кривой переходного процесса. Типовые переходные процессы. Для выбора конкретного вида переходного процесса (в зависимости от технологических требований) предложено три их типа: апериодический с минимальным временем регулирования (рис. 5.7 а), процесс с 20 % перерегулированием (рис. 6.1 б) и процесс с минимальной квадратичной площадью отклонения (рис. 6.1 в). Выбор регулятора. Под выбором регулятора следует понимать выбор закона регулирования. Для выбора закона регулирования необходимо знать:
Для выбора закона регулирования необходимо рассчитать динамический коэффициент регулирования, для статических объектов:
По графикам (рис. 6.2) для статических объектов или из табл. 6.1 для астатических объектов выбирают простейший регулятор. Далее следует оценить время регулирования при применении принятого закона. Для этого используют графики, приведенные на рис. 6.3, где определяют отношение tр/τоб (относительное время регулирования), откуда находят tр. Если найденное время регулирования превышает допустимое – переходят к более сложному закону регулирования. При рассмотрении астатического объекта регулирования можно использовать таблицы 6.1 и 6.2. Динамический коэффициент регулирования для астатических объектов | Таблица 6.2 астатических объектов | ||||||
| Закон регулирования | Типовой процесс | Закон регулирова-ния | Типовой процесс | ||||
| апериоди-ческий | 20% перерегу-лирование | с минимальной площадью | апериодический | 20% перерегу-лирование | с минимальной площадью | ||
| П | 2,9 | 1,4 | — | П | 6 | 8 | — |
| ПИ | 1,4 | 1,3 | 0,9 | ПИ | 14 | 16 | 18 |
| ПИД | 1,3 | 1,1 | 0,8 | ПИД | 9 | 12 | 13 |
В данном случае следует иметь в виду, что для данных объектов интегральный закон регулирования применять не рекомендуется, так как такая система структурно неустойчива.
- Перечислите показатели качества регулирования и дайте их характеристики.
- Выполните анализ переходного процесса в системе с И-регулятором и астатическим объектом.
- Докажите обязательное наличие остаточного отклонения при использовании П-регулятора.
- Изложите последовтельность вібора закона регулирования.
Литература к теме:[6],[7], [8]
Лекция № 7
Расчет парметров регуляторов. Устойчивость АСР
В лекции изложенывопросы
Понятие настроечных параметров регуляторов. Расчет настроек регуляторов различных законов. Понятие устойчивости систем регулирования. Критерии устойчивости и их проверка.
Выбранный закон регулирования обеспечит переходный процесс с требуемыми показателями качества при определенных значениях настроечных параметров регулятора. В соответствие с законами регулирования настроечными параметрами регуляторов являются.
Для П – регулятора:
Дли И – регулятора:
Для ПИ – регулятора:
Для ПИД – регулятора:
Настроечные параметры регуляторов можно рассчитывать несколькими способами, как графическими, так и аналитическими. Достаточная для практических целей точность достигается при использовании формул, приведенных табл. 7.1и 7.2
В лекции рассмотрен конкретный примеррасчта параметров регулятора.
Устойчивость систем регулирования
Устойчивость замкнутой АСР – важнейшее требование к системам. Под устойчивостью АСР следует понимать, что при любом реальном возмущении на систему, регулируемая величина при переходном процессе не будет бесконечно отклоняться от заданного значения.
Существует несколько критериев устойчивости САР.
Наиболее распространен критерий Найквиста, который позволяет осуществить оценку устойчивости замкнутых систем управления по амплитудно-фазовой частотной характеристике (АФЧХ) разомкнутой системы.
Критерий Найквиста имеет две формулировки. Наиболее проста в применении следующая: если система автоматического управления устойчива в разомкнутом состоянии, то для ее устойчивости в замкнутом состоянии необходимо и достаточно, чтобы АФЧХ разомкнутой системы W(jw) при изменении w от нуля до бесконечности не охватывала точку с координатами (-1; j0) комплексной плоскости.
Таблица 7.1 Формулы для расчета настроек непрерывных регуляторов при работе со статическими объектами.
| Регулятор | Типовой процесс | ||
| апериодический | 20% перерегулирование | минимальная квадратичная площадь | |
| И |  |  |  |
| П |  |  |  |
| ПИ |  |  |  |
| ПИД |  |  |  |
Таблица 6.2 Формулы для расчета настроек непрерывных регуляторов при работе с астатическими объектами.
| Регулятор | Типовой процесс | ||
| апериодический | 20% перерегулирование | минимальная квадратичная площадь | |
| П |  |  | |
| ПИ |  |  |  |
| ПИД |  |  |  |
При использовании данного критерия необходимо построить годограф Найквиста (амплитудно-фазовая частотная характеристика) разомкнутой системы и убедиться, что годограф не охватывает точку с координатами (-1; j0).
В лекции рассмотрен численный пример проверки устойчивости АСР
Контрольные вопросы.
- Укажите основные параметры настроек регуляторов.
- Представьте последовательность определения настроечных параметров регулятора.
- Объясните понятие устойчивости систем регулирования.
- Представьте последовательность проверки АСР на устойчивость с помощью критерия Найквиста
Видео:Теория автоматического регулирования. Лекция 3. Временные характеристики САУСкачать

Законы автоматического регулирования
Видео:ПИД регулятор - принцип работы.Скачать

Законы автоматического регулирования
Может оказаться, что одни автоматические системы хорошие, а другие плохие, то казалось бы всегда нужно использовать только самые хорошие, а о других — плохих не следовало бы даже. и говорить. Сначала необходимо разобраться с тем, что считать хорошие, а что плохие автоматические системы. Вообще-то хороший автоматический регулятор это такой, который обеспечивает получение достаточно хороших характеристик процесса автоматического регулирования и вместе с тем прост по своей конструкции. Нужно иметь в виду и то, что различные объекты регулирования имеют неодинаковые характеристики, и поэтому автоматический регулятор, обеспечивающий удовлетворительную работу одного из них, может быть непригодным для другого. Это тоже необходимо учитываться при выборе типа системы автоматического регулирования. Поэтому в различных случаях можно считать лучшими различные автоматические системы. В некоторых случаях можно обойтись простейшими, а в других — требуются более сложные системы автоматического регулирования.
Задачей автоматической системы, как уже отмечалось, является поддержание заданного значения регулируемой величины у(t) или изменение ее по определенному закону, который заранее задается или в зависимости от изменения внешних условий.
Программы могут быть функциями времени у = у(t) или параметрическими у = у(s1 , s2 , . . . t).
Примером временной программы может служить программа изменения регулируемой величины, обеспечивающая заданный режим начального разгона объекта регулирования при пуске до наступления режима нормальной эксплуатации. Например, регулятор частоты вращения коленчатого вала дизеля тепловоза. Во всех подобных устройствах в составе автоматического регулятора или автоматической системы имеется программное устройство, в которое заранее заложена требуемая временная программа.
Примером параметрической программы автоматического регулирования может служить задание требуемого значения скорости движения локомотива с поездом не во времени, а в зависимости от пройденного пути, чтобы прибыть в заданное время на данную станцию.
Большинство известных систем автоматического регулирования работают по принципу отклонения. Это значит, что она вступает в действие после того, как произошло отклонение регулируемой величины от заданного значения, как говорят, при наличии рассогласования Dx(t)между заданным x(t) и фактическим y(t) значением регулируемой величины.
Для наиболее часто применяемых систем автоматического регулирования иногда используются названия, отражающие их особенности, связанные со способом формирования в автоматической системе управляющих воздействий, которые передаются исполнительному устройству.
Пусть Dx(t), представляет отклонение регулируемой величины y(t) от заданного значения x(t), аh(t) воздействие со стороны автоматической системы на объект регулирования. Величина Dx(t)может изменяться в зависимости от времени по-разному.
Законом регулирования называется математическое выражение, описывающее зависимость между входом автоматического регулятора Dx(t) = x(t) — xoc(t) и его выходомy(t).
Различают линейные и нелинейные законы регулирования.
Все законы автоматического регулирования можно разделить на:
1. Простейшие:
— пропорциональный;
— интегральный;
— дифференциальный;
2. Промышленные:
— пропорционально-интегральный;
— пропорционально-дифференциальный;
— пропорционально-интегрально-дифференциальный.
Для линейных законов автоматического регулирования детально разработаны многочисленные прикладные методы исследования, анализа и синтеза, различные расчетные и экспериментальные приемы определения устойчивости, точности и качества работы, а также схемы технических устройств их формирования и реализации.
Пропорциональный закон. Чаще всего такой функциональной зависимостью является простая пропорциональная зависимость, при которой регулируемая величина y(t) должна воспроизводить обычно на более высоком уровне мощности изменения заданной величины x(t) или рассогласования Dx(t).
Если считать, что h(t)изменяется пропорциональноDx(t), то такой регулятор называютпропорциональнымили П-регулятором. Выражение пропорциональной зависимости между величинами h(t) и Dx(t) имеет следующий видh(t) = k Dx(t), где k — коэффициент усиления регулятора.
Пропорциональным автоматическим регулятором может служить обычное усилительное звено с изменяемым коэффициентом усиления, включенное в отрицательную обратную связь по отношению к объекту регулирования.
Проследим за тем, что происходит с исполнительным органом, когда регулируемая величина y(t)скачком изменяется на Dy и принимает значение y + Dy. В простейшем регуляторе, работающем по принципу отклонения, в процессе регулирования величина h(t) тем больше, чем больше отклонение Dx(t).
Принцип работы пропорционального регулятора
Как можно заключить из приведенной формулы, что нормальное функционирование данного регулятора возможно только в случае, когда Dx(t) > 0. Таким образом, автоматическая система имеет постоянную (статическую) ошибку, которую называют статизмом регулятора, а системаавтоматического регулирования называется статической системой.
Автоматическая система называется статической, если при любом постоянном задающем воздействии установившаяся ошибка поддержания регулируемой величины не равна нулю и зависит от величины этого воздействия.
Статизм выражается в процентах и определяется по формуле:
В статической по отношению к управляющему воздействию автоматической системе при воздействии, стремящемся с течением времени к некоторому значению, ошибка также стремится к постоянному значению, зависящему от значения управляющего воздействия, т. е. статическая автоматическая система не может обеспечить постоянства регулируемой величины при переменной во времени нагрузке.
Говоря о статической ошибке регулирования, считают, что после каждого изменения внешнего возмущения или отклонения от заданного режима работы, которое вызывается другими причинами, снова устанавливается постоянное значение регулируемой величины, пусть не то, что было раньше, но постоянное, и остается дальше неизменным.
Статическая автоматическая система имеет нулевой порядок астатизма. Это означает, что в прямой цепи автоматического регулирования нет интегрирующих звеньев. Она может содержать только статические звенья: усилительные, форсирующие или колебательные.
Для повышения точности поддержания заданного значения регулируемой величины, как следует из приведенного уравнения, увеличивают коэффициент усиления k. Однако при этом может возрасти динамическая погрешность, так как даже малое изменение регулируемой величины приводит к значительному изменению управляющего воздействия h(t), что может неблагоприятно сказаться на характеристиках переходных процессов, вызывая дополнительные колебания регулируемой величины.
Интегральный закон. С тем, чтобы исключить указанный недостаток систем автоматического регулирования прямого действия, были созданы автоматические системы непрямого действия, в которых между чувствительным элементом и исполнительным органом включается дополнительное звено (в большинстве случаев выполняющее операцию интегрирования погрешности регулирования Dx(t), работающее с независимым источником энергии). Это может быть гидравлический или пневматический сервомотор, электродвигатель постоянного или переменного тока и т. п. В интегральных регуляторах (И-регуляторах) управляющее воздействие формируется по следующему закону
Интегральным регулятором может служить интегрирующее звено с переменным передаточным коэффициентом в обратной связи.
Принцип работы интегрального регулятора
Переходный процесс в автоматической системе с И-регулятором характеризуется отсутствием статической ошибки регулирования и наибольшим значением отклонения регулируемой величины от установившегося значения по сравнению с другими законами регулирования. И-регуляторы в практике автоматического регулирования не применяются, т. к. они обладают плохими динамическими качествами и в большинстве случаев способствуют возникновению в автоматической системе незатухающих колебаний.
Пропорционально-интегральный закон. Инженеры и ученые давно поняли, что статическая автоматическая система не может быть абсолютно точной, если иметь в виду сведение к нулю статической ошибки, а интегральные регуляторы способствуют возникновению колебательных режимов. Тогда начались поиски способов улучшения работы автоматических систем. Было замечено, что отрицательное влияние на динамические свойства автоматической системы оказывают инерционные элементы, особенно в регуляторах прямого действия.
В процессе регулирования пропорционально-интегральной автоматической системы (ПИ-регуляторы) осуществляется два действия: одно, характерное для П-регулятора, следовательно, можно говорить о П-составляющей процесса регулирования, и второе, осуществляющееинтегрирование величины рассогласования Dx(t) интегральная составляющая.
В ПИ-регуляторах регулирующее воздействие формируется по следующему закону.
Пропорционально-интегральный закон регулирования представляет собой параллельное соединение пропорциональной и интегральной составляющих.
Пропорционально-интегральный регулятор сочетает в себе достоинства пропорциональных и интегральных законов автоматического регулирования, а именно: пропорциональная составляющая обеспечивает достаточное быстродействие регулятора, а интегральная составляющая ликвидирует статическую ошибку регулирования.
В начале процесса автоматического регулирования основную роль играет пропорциональная составляющая, так как интегральная составляющая зависит не только от абсолютного значения рассогласования между заданным и фактическим значением регулируемой величины, но и от времени. С увеличением времени возрастает роль интегральной составляющей, обеспечивающей устранение статической ошибки.
Подбором коэффициентов k1 и k2 можно изменять удельный вес каждой составляющей.
При использовании такой автоматической системы полностью устраняется статическая погрешность регулирования. Автоматическая система является астатической, в которой Dx(t) = 0.
Автоматическая система называется астатической, если при любом постоянном задающем или возмущающем воздействии установившаяся ошибка поддержания регулируемой величины равна нулю и не зависит от величины этого воздействия.
Астатические системы могут быть первого, второго и более высокого порядка астатизма.
Астатическая система первого порядка не имеет ошибки по положению, однако имеют постоянную ошибку по скорости и возрастающую ошибку по ускорению.
Астатическая система второго порядка не имеет ошибок по положению и по скорости, однако имеют постоянную ошибку по ускорению.
Автоматическая система будет астатической по отношению к управляемому воздействию, если при внешнем воздействии, стремящемуся к установившемуся значению, ошибка стремится к нулю независимо от значения внешнего воздействия. Статические системы обычно имеют менее сложное конструктивное решение, чем астатические. Они обладают погрешностью в поддержании постоянства значения регулируемой величины при разных внешних нагрузках. Изменение регулируемой величины, которое вызывает у статической системы перемещение управляемого органа из одного предельного положения в другое, является важнейшей характеристикой статической системы и называется его неравномерностью. Отношение этой неравномерности к номинальному значению регулируемой величины называют степенью неравномерности (коэффициентом статизма или статизмом).
Если иметь в виду отсутствие статической погрешности регулирования, то такая автоматическая система является абсолютно точной. Но, как показал опыт, при такой схеме построения автоматической системы трудно получить удовлетворительные динамические качестварегулирования. Это обусловлено тем, что к положению нового равновесного состояния рассогласование Dx(t) должно приближаться с нулевой скоростью. Иначе в автоматической системе возникают незатухающие колебания регулируемой величины. В общем возможности применения таких автоматических систем весьма ограничены.
В любом автоматическом регуляторе имеется внутренняя обратная связь, благодаря которой золотник принудительно возвращается в положение перекрыши, т. е. в равновесное состояние. Такой регулятор обеспечивает хорошие динамические свойства, но при его использовании возникает статическая ошибка регулирования.
Астатическая система первого порядка имеет один интегратор в прямой цепи регулирования. После завершения переходного процесса точность регулирования обеспечивается благодаря свойствам интегратора как запоминающего устройства (память идеального интегратора бесконечна).
Введение в автоматическую систему двух интегрирующих звеньев позволяет получить управление по ускорению. Система с астатизмом второго порядка благодаря свойством интеграторов точно воспроизводит и установившемся процессе постоянные и линейно возрастающие воздействия. Воздействие, изменяющееся с постоянным ускорением, автоматическая система воспроизводит (копирует) с постоянной динамической ошибкой, называемой ошибкой по ускорению.
Таким образом, порядок астатизма по отношению к задающему воздействию легко определить непосредственно по функциональной схеме автоматической системы. Для этого автоматическую систему путем структурных преобразований следует привести к одноконтурной и определить количество интегрирующих звеньев между входом и выходом.
Пропорционально-интегрально-дифференциальный закон. Положительные качества всех рассмотренных автоматических систем объединяет пропорционально-интегрально-дифференциальный закон регулирования или ПИД-регуляторы. Мысль инженеров работала над тем, как устранить отмеченные выше недостатки, или если их полностью устранить нельзя, то хотя бы уменьшить их вредное влияние на процесс регулирования. Было решено использовать воздействия по производной сигнала рассогласования.
ПИД-регулятор сочетает в себе достоинства всех простейших законов автоматического регулирования:
— высокое быстродействие благодаря наличию пропорциональной составляющей;
— высокую точность благодаря интегральной составляющей;
— малое время переходного процесса благодаря дифференциальной составляющей.
Иногда говорят, что такие регуляторы работают с предварением, т. е. он вступает в действие тогда, когда еще отклонение не произошло.
Благодаря воздействию по производной осуществляется предварение формирования управляющего воздействия, а благодаря сигналу по интегралу снимается статическая погрешность регулирования.
В этом случае управляющее воздействие формируется согласно закону
На установившихся режимах работы всегда, как бы ни изменялись возмущения, регулируемая величина остается неизменной. Этот регулятор в начале переходного процесса, вызванном изменением нагрузки, работает как ПИ-регулятор, что является благоприятным для динамических свойств системы, а затем в ходе переходного процесса, действие обратной связи ослабевает, что позволяет работать без статической погрешности. Такая обратная связь называется гибкой обратной связью.
Принцип работы пропорционально-интегрально-дифференциального регулятора
Необходимо отметить, что применение автоматических регуляторов с дифференциальными составляющими, несмотря на их достоинства, не всегда целесообразно, а иногда и недопустимо. Так, для объектов с большим запаздыванием по каналу регулирования бесполезно вводить воздействие по производной от регулируемой величины, так как этот сигнал будет поступать в автоматический регулятор по истечении времени запаздывания после прихода возмущения, за которые в объекте регулирования могут накопиться большие отклонения. В таких случаях ПИД-регулятор может привести к неустойчивости автоматической системы
Использование нелинейных законов автоматического регулирования, определяемых разнообразными нелинейными уравнениями состояния значительно расширяет возможности целесообразного изменения качества процессов автоматического регулирования и точности работы автоматических систем. Это должно быть ясно из общих принципиальных соображений, так как область нелинейных уравнений значительно богаче и разнообразнее, чем линейных.
Несмотря на то, что общей теории нелинейных законов автоматического регулирования нет, исследования и опыт применения отдельных частных видов этих законов говорят об их большой практической эффективности.
Важным отличием нелинейных законов автоматического регулирования от линейных является то, что они придают автоматической системе принципиально новые свойства. Если при линейном законе автоматического регулирования всегда вырабатывается сигнал, пропорциональный входной переменной или ее производной, то при нелинейном законе может существенно изменяться сам характер действия автоматической системы на объект регулирования в зависимости от величины входного воздействия. Другими словами, если для линейных автоматических систем изменение размера отклонения Dx(t) — это изменение только масштаба, но не формы процессов, то в нелинейной автоматической системе при этом может существенно изменяться и форма процессов, вплоть до принципиальных качественных изменений картины происходящих процессов. Эти особые свойства нелинейных законов можно выгодно использовать в технике автоматического регулирования.
Нелинейные законы автоматического регулирования разделяют на:
— функциональные нелинейные законы автоматического регулирования;
— логические нелинейные законы автоматического регулирования;
— оптимизирующие нелинейные законы автоматического регулирования;
— параметрические нелинейные законы автоматического регулирования.
Рассмотрим отдельно каждый из указанных нелинейных законов автоматического регулирования.
Функциональные нелинейные законы автоматического регулирования предполагают изменение управляющего воздействия h(t) на объект регулирования, выражающегося в виде нелинейной функции от отклонения регулируемой величины Dx(t). Данный класс автоматических систем может содержать в себе как статические, так и динамические нелинейности
Нелинейный закон автоматического регулирования может включать нелинейности от выходной величины у(t). Подобные динамические члены нелинейного закона автоматического регулирования различно влияют на демпфирующие свойства автоматической системы в переходных режимах в зависимости от скорости отклонения регулируемой величины Dx(t). Они могут существенно улучшить динамическую точность автоматической системы в различных режимах вынужденного движения, воспроизведения различных форм задаваемых входных сигналов. а также при случайных воздействиях.
Отметим также, что функциональные нелинейные законы автоматического регулирования могут быть связаны не только с изменением параметров в зависимости от размеров входных воздействий, но и с изменением структуры автоматической системы.
Логические нелинейные законы автоматического регулирования реализуются с помощью не функциональных, а более сложных логических устройств. Построение простейшего логического нелинейного закона автоматического регулирования может сводиться к выбору того или иного способа обработки сигнала рассогласования Dx(t) в зависимости от поставленных перед автоматической системой задач и требуемого качества регулирования.
Логические нелинейные законы автоматического регулирования могут быть связаны также с изменением структуры автоматической системы. Например, при помощи логического устройства можно включать и выключать сигналы управления по первой и второй производными или интегралу, в зависимости от сочетания значений отклонения сигнала рассогласования Dx(t).
В общем случае срабатывание переключающего устройства в автоматической системе с переменной структурой может происходить от нескольких входных величин. При этом кроме основной нелинейности, возникающей за счет переключения структуры, дополнительно могут иметься какие-либо нелинейные свойства в отдельных других звеньях автоматического регулятора или объекта регулирования.
Оптимизирующие нелинейные законы автоматического регулирования основаны на использовании классических вариационных методов или на их основе принципа максимума, или методов динамического программирования таким образом, чтобы автоматическая система имела максимум быстродействия или минимум ошибки, или же экстремум другой величины с учетом ограничений, накладываемых в реальной автоматической системе на отдельные координаты.
Как правило, при этом приходят к нелинейным законам автоматического регулирования, хотя можно оптимизировать коэффициенты линейного закона. Часто оптимальный закон автоматического регулирования состоит в переключении управляющего воздействия h(t) с одного максимально возможного значения на другое. Моменты переключения определяются сложными комбинациями значений нескольких переменных и их производных.
Параметрические нелинейные законы автоматического регулирования формируют управляющее воздействие в виде нелинейной функции текущих координат, в которых задается параметрическая программа.
📽️ Видео
ОПИ-17ДО. Типовые законы регулированияСкачать

1) ТАУ (Теория автоматического управления) для чайников. Часть 1: основные понятия...Скачать

Обзор ПИД регулятора, пропорциональное, интегральное, дифференциальное регулирование. ПИД-регулятор.Скачать

ЧАПЛЫГА: ЗАПАД ВЕДЁТ УКРАИНУ К ПОРАЖЕНИЮ? УПРАВА НА ОРБАНА, КОНЕЦ БЕСОГОНА, КЛИНЦЫ ПЫЛАЮТСкачать

Как влияют параметры ПИД-регулятора на процесс? Ответ на вопрос 4Скачать

Закон БернуллиСкачать

Теория автоматического управления. Лекция 16. Настройка ПИД-регулятораСкачать

Обзор недорогих китайских осциллографов Нужны ли ониСкачать

Cопротивление, резисторы и закон Ома. Самое понятное объяснение!Скачать

Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Дельта функция, Леннаучфильм, 1985Скачать

Законы регулирования 1Скачать

Уроки Ардуино. ПИД регуляторСкачать

ПИ, ПИД-регулятор и автоматикаСкачать

ОПИ-17ДО. Типовые законы регулирования-2Скачать

 .
. (5.1)
(5.1) ,
, ,
, 
 (5.2)
(5.2)
 ,
,  (5.3)
(5.3)
 , (5.4)
, (5.4) . (5.5)
. (5.5)
 , (5.6)
, (5.6)
 (5.9)
(5.9) (5.9)
(5.9)
 ,
,
 ; для астатических объектов
; для астатических объектов  .
.





























