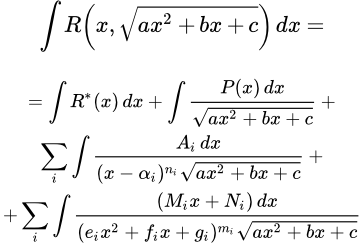- Интегрирование рациональной функции от квадратного корня из квадратного трехчлена
- Метод интегрирования
- Доказательство
- Пример
- Интегрирование иррациональных функций: способы и примеры решений
- В подынтегральном выражении — различные дробно-рациональные функции
- Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
- Корень из квадратного трёхчлена и подстановки Эйлера
- Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
- Интегралы от дифференциального бинома и подстановки Чебышева
- Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
- Частный случай квадратичных иррациональностей
- Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
- Интеграл от корня квадратного уравнения
- Контакты
- 📺 Видео
Видео:8.1. Интеграл от иррациональной функции ∫√(ax^2+bx+c) dxСкачать
Интегрирование рациональной функции от квадратного корня из квадратного трехчлена
Видео:Неопределенный интеграл от иррациональной функции: 2 способа решения.Скачать
Метод интегрирования
Здесь мы рассматриваем интегралы вида:
,
где R – рациональная функция.
Ранее мы рассмотрели интегралы с квадратным корнем от трехчлена трех типов.
(i) Подробнее >>>
(ii) Подробнее >>>
(iii) Подробнее >>>
Здесь Pn ( x ) – многочлен степени n от x .
Покажем, что любой интеграл от рациональной функции вида , можно выразить через интегралы (i), (ii) и (iii) и интеграл от рациональной функции .
Доказательство
Прежде всего заметим, что любая целая степень от квадратного корня является или многочленом (для четных степеней), или произведением многочлена на корень .
Действительно, имеем.
;
;
;
;
И так далее.
Любую рациональную функцию можно представить в виде дроби, в числителе и знаменателе которой стоят суммы конечного числа членов от целочисленных степеней ее аргументов.
.
Поскольку целая степень от квадратного корня является или многочленом от x , или произведением многочлена на корень, то
,
где P ( x ) , Q ( x ) , V ( x ) , W ( x ) – многочлены от x .
Умножим числитель и знаменатель на и применим формулу ( a + b )( a – b ) = a 2 – b 2 .
В знаменателе имеем.
.
Как видно, знаменатель становится многочленом, который мы обозначили через U ( x ) . В числителе по прежнему имеется сумма произведений целочисленных степеней от x и . Поэтому числитель имеет прежний вид , где P * ( x ) , Q * ( x ) — многочлены. Таким образом, имеем
,
где R ( x ) – рациональная функция, Q ** ( x ) – многочлен.
Если степень многочлена Q ** ( x ) больше, чем у многочлена U ( x ) , то выделим целую часть. Тогда
,
где P ** ( x ) – многочлен, – правильная дробь. Имеем . Правильную дробь разложим на простейшие. Это даст сумму членов вида и .
Подставляя все члены разложения в и интегрируя получаем, что интеграл выражается через интегралы вида , , и .
Что и требовалось доказать.
Видео:8.2 Интегралы с корнем / интегралы с квадратным трехчленомСкачать
Пример
Умножим числитель и знаменатель на .
.
Ищем решение оставшегося интеграла в виде
.
Дифференцируем по x .
.
Умножая на , имеем
.
Сравнивая левую и правую части, находим значения коэффициентов.
2 A = 1 , A = 1/2 ;
B = 0 ;
D – A = – 1 , D = A – 1 = – 1/2 .
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов . Опубликовано: 16-02-2015
Видео:СЛОЖИТЕ ДВА КОРНЯСкачать
Интегрирование иррациональных функций: способы и примеры решений
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Рассмотрим интегралы от иррациональных функций, то есть функций, содержащих переменную (обычно икс) под корнем или, что то же самое — в дробной степени. Интегралы от таких функций с помощью подстановок приводятся к интегралам от рациональных функций и могут быть проинтегрированы окончательно.
Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать
В подынтегральном выражении — различные дробно-рациональные функции
Разберём интегралы, где в подынтегральном выражении переменная присутствует под корнем. В формально обобщённом виде речь идёт об интегралах вида
,
В примерах мы увидим, что переменная икс, присутствующая под корнем, присутствует там без степени. В примере 3 икс присутствует также в квадрате, но при этом — не по корнем. То есть корни отдельно, степени — отдельно.
В этом случае важное значение имеет наименьшее общее кратное чисел λ , . μ (или общий знаменатель, если эти числа дробные). Обозначим это наименьшее общее кратное (общий знаменатель) через n . Рассматриваемые интегралы от иррациональных функций можно найти, используя следующую подстановку:
Тогда каждая дробная степень «икса» выразится через целую степень «тэ» и подынтегральная функция преобразуется в рациональную функцию от «тэ».
Пример 1. Найти интеграл от иррациональной функции 
.
Решение. Преобразуем все корни икса в степени. Выписываем степени при иксе в подынтегральном выражении — все, которые там находим:
.
Находим наименьшее общее кратное знаменателей этих чисел: 4.
Поэтому используем следующую подстановку:
Подставляем и преобразуем:
Возвращаясь к переменной икс, окончательно находим:
.
Пример 2. Найти интеграл от иррациональной функции 
.
Решение. Используем следующую подстановку:
Подставляем и преобразуем:
Интегрируем и получаем:
Возвращаясь к переменной икс, окончательно находим:
.
Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
Пример 3. Найти интеграл от иррациональной функции 
.
Пример 4. Найти интеграл от иррациональной функции
.
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать
Корень из квадратного трёхчлена и подстановки Эйлера
Если дан интеграл иррациональной функции вида
,
то есть в подынтегральном выражении — корень из квадратного трёхлчена, то можно воспользоваться подстановками Эйлера.
,
В зависимости от характера корней квадратного уравнения используются следующие подстановки Эйлера.
1. Если x 1 , x 2 — действительные числа (не комплексные), то используется подстановка
(первая подстановка Эйлера).
2. Если x 1 , x 2 — комплексные числа и a > 0 , то используется подстановка
(вторая подстановка Эйлера).
3. Если x 1 , x 2 — комплексные числа и c > 0 , то используется подстановка
(третья подстановка Эйлера).
Пример 5. Найти интеграл от иррациональной функции 
.
Решение. Разложим квадратный трёхчлен на множители:
Используем первую подстановку Эйлера:
Интегрируем и получаем:
Возвращаясь к переменной икс, сначала долго занимаемся преобразованием выражений, а затем окончательно находим:
Пример 6. Найти интеграл от иррациональной функции 
.
Используем вторую подстановку Эйлера:
Интегрируем и получаем:
.
Возвращаясь к переменной икс, окончательно находим:
.
Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
Пример 7. Найти интеграл от иррациональной функции 
.
(использовать третью подстановку Эйлера).
Видео:8.3 Интегрирование иррациональных функций.Скачать
Интегралы от дифференциального бинома и подстановки Чебышева
,
где m, n, p — рациональные числа (целые или дробные), называются интегралами от дифференциального бинома. В примерах мы увидим, что в подынтегральных выражениях переменная икс присутствует не только под корнем: она под корнем, но ещё и в степени. В этом главное отличие рассматриваемых интегралов от тех, которые были рассмотрены в первом параграфе.
Чтобы найти такие интегралы, используются подстановки Чебышева.
1. Если p — целое число, то используется подстановка
,
где k — наименьшее общее кратное знаменателей m и n.
2. Если 
— целое число, то используется подстановка
,
где s — знаменатель дроби p .
3. Если 
— целое число, то используется подстановка
,
где s — знаменатель дроби p .
Русский математик П.Л. Чебышев доказал, что только в перечисленных трёх случаях интеграл от дифференциальных биномов с рациональными показателями степени выражается через элементарные функции.
Пример 8. Найти интеграл от иррациональной функции 
.
Преобразуем корни в степени и избавимся от дроби:
Здесь p = -1 (целое число). Чтобы избавиться от степени икса в скобках, сделаем промежуточную подстановку
:
.
Теперь сделаем следующую подстановку:
Подставляем и получаем:
Возвращаемся к переменной z :
.
Возвращаясь к переменной икс, окончательно находим:
.
Пример 9. Найти интеграл от иррациональной функции 
.
Преобразуем корни в степени и избавимся от дроби:
.
Здесь m = 3 , n = 2 , 
, 
(целое число).
Cделаем промежуточную подстановку
:
.
Теперь, чтобы избавиться от дробной степени выражения в скобках, сделаем следующую подстановку:
.
Интегрируем и получаем:
.
Возвращаемся к переменной z :
.
Возвращаясь к переменной икс, окончательно находим:
.
Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
Пример 10. Найти интеграл от иррациональной функции 
.
— целое число.
Видео:8.8. Интеграл от рациональной функции с корнямиСкачать
Частный случай квадратичных иррациональностей
Рассмотрим интеграл от иррациональной функции вида
, (1)
где в знаменателе — квадратный корень из квадратного трёхчлена.
Чтобы проинтегрировать любой интеграл такого вида, необходимо уметь находить интегралы 
и 
.
Формула для нахождения первого из них:
(2)
Второй интеграл находится по формуле
(3)
Формулы (2 и (3) можно условно считать табличными интегралами. Если в подкоренном выражении интеграла (1) выделить полный квадрат, то при a > 0 это выражение примет вид
После подстановки t = x – m в первом случае интеграл (1) приводится к интегралу (3), во втором – к интегралу (2).
Пример 11. Найти интеграл от иррациональной функции
Решение. Выделим в подкоренном выражении полный квадрат:
Произведя теперь подстановку
причём при интегрировании воспользовались формулой (3). Возвращаясь к старой переменной, окончательно получим
Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
Пример 12. Найти интеграл от иррациональной функции
Видео:Примеры решения определенных интеграловСкачать
Интеграл от корня квадратного уравнения
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |
