Иллюстрация уравнения бернулли диаграмма напоров (8 видео)

Иллюстрация уравнения Бернулли. Построение диаграммы напоров. Изучение закона сохранения энергии по визуально наблюдаемой пьезом. Отчет по лабораторной работе 5 Тема Иллюстрация уравнения Бернулли. Построение диаграммы напоров. Изучение закона сохранения энергии по визуально наблюдаемой пьезометрической линии при сужении трубопровода и расширении

Название	Отчет по лабораторной работе 5 Тема Иллюстрация уравнения Бернулли. Построение диаграммы напоров. Изучение закона сохранения энергии по визуально наблюдаемой пьезометрической линии при сужении трубопровода и расширении
Анкор	Иллюстрация уравнения Бернулли. Построение диаграммы напоров. Изучение закона сохранения энергии по визуально наблюдаемой пьезом
Дата	03.11.2021
Размер	0.5 Mb.
Формат файла
Имя файла	laba_5_gidravlika.docx
Тип	Отчет #262297

Иллюстрация уравнения бернулли диаграмма напоров

С этим файлом связано 1 файл(ов). Среди них: Индивидуальное задание по Анатомия и физиология центральной нерв.

Показать все связанные файлы Подборка по базе: Бланк отчета. Практической работы 2.docx, форма титульного листа отчета по практике.pdf, Производстенная практика. Отчет.docx, Методические указания по выполнению лабораторной работы №4.docx, Дневник по практике с отчетом.doc, Анеля3 отчет плагиат.docx, _ СКАН-КОПИЯ БУХГАЛТЕРСКОЙ ОТЧЕТНОСТИ за 9 месяцев 2021 г.pdf, Лексина А.В. ДО-152 Отчет по учебной практике..docx, 17__ Инструкция по охране труда при работе на персональном компь, 1 з класс отчет за полугодие.doc

Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования

Санкт-Петербургский горный университет

Отчет по лабораторной работе №5

Тема: «Иллюстрация уравнения Бернулли. Построение диаграммы напоров. Изучение закона сохранения энергии по визуально наблюдаемой пьезометрической линии при сужении трубопровода и расширении»

Выполнили: студент гр.НБ-19 _________ /Шатохин А.С./

Проверил: ассистент _________ /Касьянов А.В./

Изучение закономерностей течения жидкости (уравнения Бернулли) в сложном трубопроводе при последовательном соединении участков разного диаметра. Экспериментальное построение напорной характеристики, построение напорной и пьезометрической линий сложного трубопровода. Изучение влияния геометрической высоты трубопровода на величины полного и гидростатического напора и расход через трубопровод.

II. Теоретические основы работы

На практике достаточно часто встречаются «сложные» трубопроводы, состоящие из участков различного диаметра, соединительных деталей и т.д. Исследовать гидравлические режимы таких систем можно с использованием диаграммы напоров. Особую важность графическое построение напорной линии приобретает для протяженных линейных трубопроводов – водоводов, нефтепроводов и т.д.

Уравнение Бернулли в общем виде записывается следующим образом:

+ ∙ = + ∙ +Δ , (1)

где – геодезический напор в сечении 1; – пьезометрический напор в сечении 1 (удельная потенциальная энергия давления); ∙ – скоростной напор в сечении 1 (удельная кинетическая энергия ); Δ – потери напора на трение между сечениями. Для сечения 2 обозначения аналогичны.

Уравнение Бернулли является одной из форм закона сохранения энергии. Исходя из него, очевидно, что линия полного напора может только падать вдоль трубопровода, не имеющего дополнительных подкачек, поскольку энергия потока безвозвратно расходуется на трение. Линия же пьезометрических напоров может как падать, так и расти.

Линию пьезометрических напоров строят по показаниям пьезометров. Дополнив в каждой точке линию пьезометрических напоров на величину скоростных напоров – получают линию полного напора. Все построения осуществляются при фиксированном расходе.

Средняя скорость жидкости:

(2)

(3)

(4)

Потребные пьезометрические напоры для каждого участка:

(5)

(6)

(7)
Потребный пьезометрический напор сложного трубопровода:

(8)

Потребные полные напоры участка и трубопровода в целом:

∙ (9)

Полный напор сложного трубопровода с последовательным соединением:

(10)

Полный напор в сечении:

(11)

Зависимость потерь полного напора в местных сопротивлениях от числа Рейнольдса:

А) для плавного сужения

Δ ∙ ∙ (12)

Δ ∙ ∙ (13)

Величины коэффициентов сопротивлений плавного сужения и внезапного расширения:

(14)

(15)

Работа выполнялась на учебном стенде «Основы механики жидкости» (ОМЖ-016-10ЛР-01) (рисунки 1-2).

Рисунок 1 – Схема учебного стенда «Основы механики жидкости» (ОМЖ-016-10ЛР-01)

Рисунок 2 — Типовой комплект учебного оборудования ОМЖ-016-10ЛР-01. Общий вид.

Таблица 1. Состав учебного стенда «Основы механики жидкости»

Обозначение	Наименование
Б1	Бак
Б2	Бак накопительный
Н1, Н2	Насос циркуляционный центробежный
ЕМ1	Мерная емкость
Т1, Т2	Простой трубопровод
Т3. Т4	Сложные трубопроводы
КР1…КР8	Кран шаровый
З1…З7	Задвижка клиновая
Д1	Мерная диафрагма
РМ	Расходомер
ТР1	Тройник

Порядок выполнения работы и формулы для вычислений

Сложный трубопровод состоит из трех последовательно соединенных прозрачных труб из органического стекла с внутренними диаметрами d_I =15 мм, d_II =10 мм, d_III =15мм. Расстояния между точками отбора и схему подключения пьезометров см. рисунок 1. Для исследования влияния изменений геометрического напора конструкцией стенда предусмотрена возможность изменения угла наклона оси трубопровода к горизонту. Переходы между участками трубопровода выполнены в виде конусов (конфузора и диффузора).

Примеры вычислений для опыта 1

Средняя скорость жидкости (формула 2):

1,07 м/c

Критерий Рейнольдса (формула 3):

1799,5

Скоростной напор (формула 4):

Потребные пьезометрические напоры для каждого участка

Потребный пьезометрический напор сложного трубопровода

(8)

Потребные полные напоры участка и трубопровода в целом (формула 9):

∙ мм

Полный напор сложного трубопровода с последовательным соединением (формула 10):

Рисунок 3 – График зависимости полного напора сложного трубопровода от расхода жидкости
Полный напор в сечении (формула 11):

мм

Зависимость потерь полного напора в местных сопротивлениях от числа Рейнольдса, графики которых представлены на рисунках 4 и 5:

А) для плавного сужения (формула 12)

Δ 1042,21-1042,21=41 мм

Б) для плавного расширения (формула 13)

Δ 997,21 1467,30 -470,09 мм

Рисунок 4 – График зависимости напора для плавного сужения от числа Рейнольдса (Re)

Рисунок 5 – График зависимости напора для плавного расширения от числа Рейнольдса (Re)

Величины коэффициентов сопротивлений плавного сужения и внезапного расширения (формулы 14 и 15), графики которых представлены на рисунках 6 и 7:

-8082

Рисунок 6 – График зависимости коэффициента сопротивления плавного сужения от числа Рейнольдса (Re)

Рисунок 7 – График зависимости коэффициента сопротивления внезапного расширения от числа Рейнольдса (Re)
Аналогичные расчеты проводятся для всех экспериментов №1-10 и результаты расчетов заносятся в таблицу 2 и на их основе строятся графики, представленные на рисунках 2-4.
Таблица 1.1 – Экспериментальные данные

л/с

H₁₂, мм

H₁₃, мм

H₁₄, мм

H₁₅, мм

H₁₆, мм

H₁₇, мм

15,9

0,1887

900

896

870

866

877

875

13,4

0,2239

850

846

782

770

797

791

11,8

0,2542

800

795

690

672

714

706

11,7

0,2564

750

743

610

580

642

635

11,2

0,2679

700

690

517

476

556

546

Продолжение таблицы 1.1

, м/с	, м/с	, м/c	Re₁	Δh₁, мм	Δh₂, мм	Δh₃, мм
1,07	1,07	2,40	1799,50	1799,50	2699,26	4	4	2
1,27	1,27	2,85	2135,23	2135,23	3202,85	4	12	6
1,44	1,44	3,24	2424,76	2424,76	3637,13	5	18	8
1,45	1,45	3,26	2445,48	2445,48	3668,22	7	30	7
1,52	1,52	3,41	2554,65	2554,65	3831,98	10	41	10

Δh₁₃₁₄, мм	Δh₁₅₁₆, мм	H₁, м	, м	, м	, м	H_потр
26	11	0,0581	0,0581	0,2942	30	15	2	47
64	27	0,0818	0,0818	0,4141	68	39	6	113
105	42	0,1055	0,1055	0,5341	110	60	8	178
133	62	0,1073	0,1073	0,5432	140	92	7	239
173	80	0,1171	0,1171	0,5928	183	121	10	314

			∑H
146,21	131,21	590,30	867,72
231,61	202,61	834,29	1268,52
320,99	270,99	1076,14	1668,13
354,61	306,61	1093,48	1754,71
417,20	355,20	1195,65	1968,06

H₁₂	H₁₃	H₁₄	H₁₅	H₁₆	H₁₇	H_пс	H_пр	ζ_пс	ζ_пр
1046,21	1042,21	1001,21	997,21	1467,30	1465,30	41,00	470,09	705,63	-8090,5
1081,61	1077,61	984,61	972,61	1631,29	1625,29	93	658,68	1136,83	-8051,6
1120,99	1115,99	960,99	942,99	1790,14	1782,14	155	847,15	1469,25	-8030,2
1104,61	1097,61	916,61	886,61	1735,48	1728,48	181	848,87	1686,75	-7910,6
1117,20	1107,20	872,20	831,20	1751,65	1741,65	235	920,45	2006,81	-7860,2

Таблица 2.1 – Экспериментальные данные

№ л/с	H₁₂, мм	H₁₃, мм	H₁₄, мм	H₁₅, мм	H₁₆, мм	H₁₇, мм	α
1	16,1	0,21978	900	899	879	873	882	881	1
2	13,65	0,24	850	846	783	772	797	794	1
3	12,5	0,254237	800	795	695	673	718	713	1
4	11,8	0,280374	750	742	603	572	633	628	1
5	10,7	0,280374	700	690	518	473	555	544	1

, м/с	, м/с	, м/c	Re₁	Δh₁, мм	Δh₂, мм	Δh₃, мм
1,243702	1,243702	2,798329	2096,126	2096,126	3144,19	1	6	1
1,358122	1,358122	3,055775	2288,97	2288,97	3433,455	4	11	3
1,438689	1,438689	3,23705	2424,756	2424,756	3637,134	5	22	5
1,586591	1,586591	3,56983	2674,03	2674,03	4011,046	8	31	5
1,586591	1,586591	3,56983	2674,03	2674,03	4011,046	10	45	11

Δh₁₃₁₄, мм	Δh₁₅₁₆, мм	H₁, м	, м	, м	, м	H_потр
20	-9	0,078838	0,078838	0,399115	21	-3	1	19
63	-25	0,094011	0,094011	0,475931	67	-14	3	56
100	-45	0,105496	0,105496	0,534072	105	-23	5	87
139	-61	0,128301	0,128301	0,649525	147	-30	5	122
172	-82	0,128301	0,128301	0,649525	182	-37	11	156

			∑H
21,15768	-2,84232	1,798231	20,11358
67,18802	-13,812	3,951861	57,32791
105,211	-22,789	6,068144	88,49013
147,2566	-29,7434	6,299051	123,8123
182,2566	-36,7434	12,29905	157,8123

H₁₂	H₁₃	H₁₄	H₁₅	H₁₆	H₁₇	H_пс	H_пр	Ζ_пс	ζ_пр
900,02	899,02	879,00	873,00	882,00	881,00	20,02	-9,00	253,99	-114,22
850,07	846,07	782,99	771,99	797,00	794,00	63,08	-25,02	671,00	-266,12
800,11	795,11	694,98	672,98	718,01	713,01	100,13	-45,03	949,12	-426,83
750,15	742,15	602,97	571,97	633,01	628,01	139,18	-61,04	1084,77	-475,72
700,18	690,18	517,96	472,96	555,01	544,01	172,22	-82,05	1342,30	-639,50

Рисунок 8 – Пьезометрическая и напорная линии

Видео:Уравнение Бернулли гидравликаСкачать

Дистанционная лабораторная работа 5 по иллюстрации уравнения Бернулли

Цель работы. Опытное подтверждение уравнения Д. Бернулли, т. е. понижения механической энергии по течению и перехода потенциальной энергии в кинетическую и обратно (связи давления со скоростью).

Задание. На основе замеров при просмотре фильма и анализе фотографии течения жидкости в канале переменного сечения в устройстве № 4 построить линии энергий для потока и проверить их соответствие уравнению Бернулли.

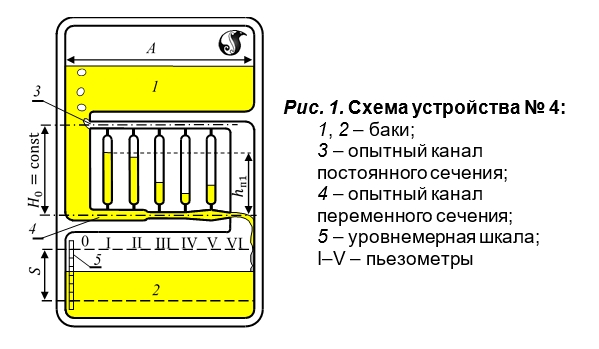
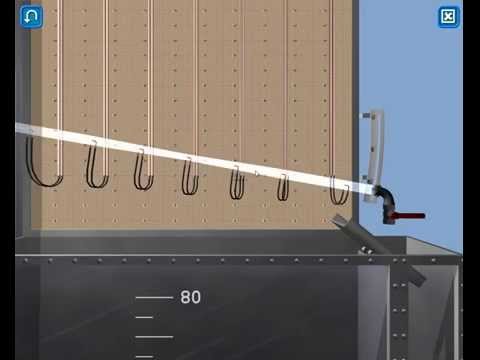
Описание устройства № 4. Устройство № 4 содержит баки 1 и 2, сообщаемые через опытные каналы постоянного 3 и переменного 4 сечений (рис. 1). Каналы соединены между собой равномерно расположенными пьезометрами I–V, служащими для измерения пьезометрических напоров в характерных сечениях. Устройство заполнено подкрашенной водой.

В одном из баков предусмотрена шкала 5 для измерения уровня воды. При перевертывании устройства, благодаря постоянству напора истечения Н о во времени, обеспечивается установившееся движение воды в нижнем канале. Другой канал в это время пропускает воздух, вытесняемый жидкостью из нижнего бака в верхний.

Порядок выполнения работы.

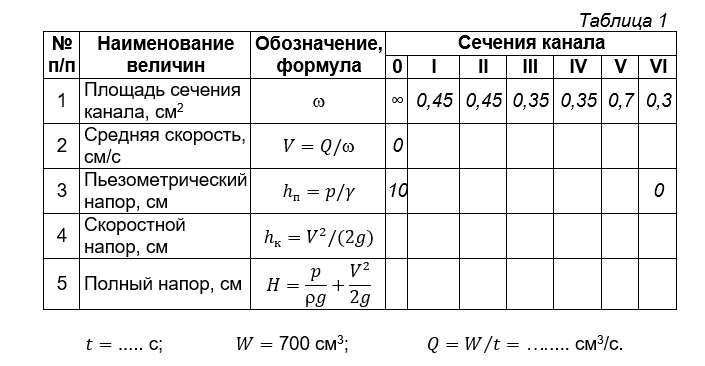
1. Зарисовать схему устройства № 4 и составить таблицу следующего вида.

2. Посмотреть фильм с демонстрацией течения воды через канал переменного сечения в устройстве № 4 и секундомером замерить время t полного опорожнения верхнего бака.

3. Под таблицей записать значение времени t t опорожнения бака, объем бака принять равным W=700 см 3 и определить расход Q=W/t Q = W t .

4. В строке (стр.) 2 рассчитать среднюю скорость течения жидкости в каждом сечении канала: V=Q / w ω Скорость в нулевом сечении (перед входом в канал) принять равной нулю.

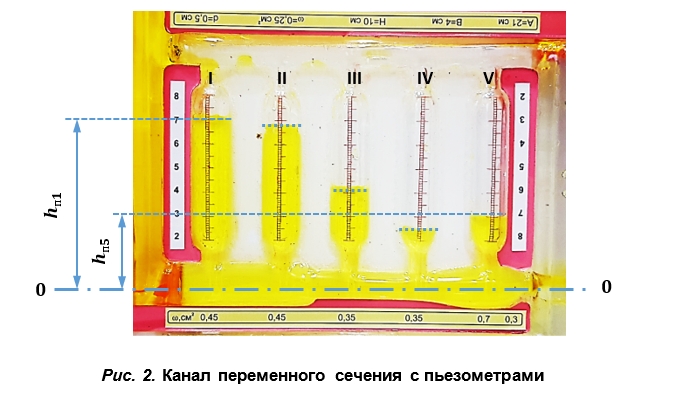
5. На фотографии канала с пьезометрами (рис. 2) снять показания пьезометров h_П1 . . . . h_П5 и записать их в стр. 3. В сечении VI пьезометрический напор равен 0.

6. В стр. 4 определить скоростной напор h_к в сечениях канала. Принять g = 981 см/с 2 .

7. В стр. 5 определить полный напор H H (полную удельную энергию) в каждом сечении. Так как опытный канал горизонтальный и плоскость сравнения 0–0 проведена через его ось, то геометрический напор z₁= z₂= 0 .

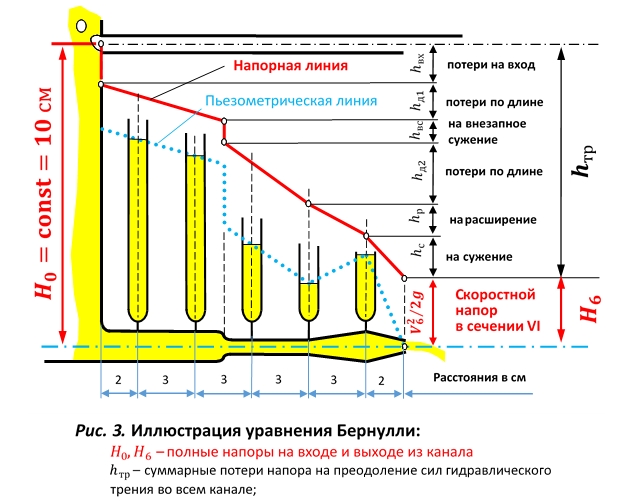
8. Вычертить в масштабе канал с осями пьезометров (рис. 3). Отложить от оси канала пьезометрические напоры h_П h _п на осях пьезометров, наметить уровни жидкости и соединить их между собой и центром выходного сечения VI , как показано на рис. 3. Получится пьезометрическая линия, показывающая изменение потенциальной энергии (давления) вдоль потока. Для получения напорной линии (линии полной механической энергии) нужно отложить от оси канала полные напоры Н и соединить полученные точки, как показано на рис. 3.

9. Проанализировать изменения полной механической H , потенциальной 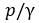и кинетической V 2 /(2g) V 2 /(2 g ) энергий жидкости вдоль потока и проверить их соответствие нижеприведенным правилам построения линий энергий, вытекающим из уравнения Бернулли.

А. Напорная линия (полный напор 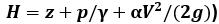постоянно понижается по течению (если на рассматриваемом участке нет насоса) ввиду необратимого преобразования механической энергии в тепловую при преодолении потоком сил гидравлического трения. Причем уклон линии (потери напора h тр ) тем больше, чем меньше сечение участка потока (см. рис. 3).

Б. Пьезометрическая линия отражает изменение потенциальной энергии (z + 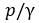) , и, в отличие от напорной, может не только понижаться, но и повышаться по течению. Это происходит при расширении потока (см. рис. 2, 3) за счет повышения давления p ввиду уменьшения скорости V . Пьезометрическая линия проходит через центр тяжести выходного сечения канала (трубопровода) при истечении жидкости в атмосферу и ниже оси канала, если давление в нем меньше атмосферного.

В. Расстояние между пьезометрической и напорной линиями численно равно кинетической энергии 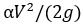α V 2 /( 2 g ) и поэтому обратно пропорционально диаметру трубы. Для участков потоков постоянного сечения средние скорости одинаковы по пути, поэтому такие линии, как правило, параллельны между собой (рис. 3). Эти линии для потоков в конфузорах (конических сходящихся патрубках) расходятся, а в диффузорах (конических расходящихся патрубках) – сходятся. В баках и водоёмах, где жидкость не движется (V=0) ( V =0) , напорная и пьезометрическая линии энергий совпадают со свободной поверхностью, если она находится под атмосферным давлением.

10. Записать выводы , где указать какие знания и навыки получены при выполнении данной работы и в каких сферах инженерной деятельности они могут быть применены.

Видео:Дистанционная работа 5 - иллюстрация уравнения БернуллиСкачать

Работа 6. Иллюстрация уравнения д. Бернулли

1. Опытное подтверждение выводов, следующих из уравнения Бернулли, то есть снижение механической энергии по течению и перехода потенциальной

Энергии в кинетическую энергию и обратно.

1. Построение на основании опытных данных пьезометрической и полной напорной линий, иллюстрирующих соответственно изменение удельной потенциальной и полной энергии вдоль потока.

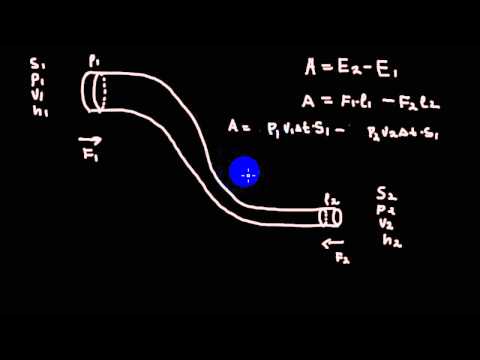
Уравнение Бернулли для элементарной струйки идеальной жидкости имеет вид:

(1)

Где z – геометрический напор (высота нормального сечения струйки относительно плоскости сравнения), м; – пьезометрически напор, м (Р – Давление в этом сечении) ; – скоростной напор, м (U – скорость в этом сечении).

Назовем Удельной энергией энергию, отнесенную к единице веса жидкости. Очевидно, что единица измерения удельной энергии – метр (Дж / Н = м).

Геометрическим напором Z Называется удельная потенциальная энергия положения жидкости.

Пьезометрическим напором Называется удельная потенциальная энергия давления жидкости.

Гидростатическим напором называется удельная потенциальная энергия жидкости.

Скоростным напором называется удельная кинетическая энергия жидкости.

Полным напором называется полная (кинетическая и потенциальная) удельная механическая энергия жидкости.

С Физической точки зрения Уравнение Бернулли для элементарной струйки идеальной жидкости выражает Закон сохранения механической энергии.

Таким образом, полная удельная механическая энергия жидкости постоянна вдоль струйки, но ее составляющие части – кинетическая и потенциальная энергии – могут изменяться. Характер этих изменений вполне определяется геометрическими параметрами струйки.

При переходе от элементарной струйки идеальной жидкости к потоку реальной вязкой жидкости необходимо учитывать потери энергии, обусловленные различными гидравлическими сопротивлениями, а также неравномерный характер распределения поля скоростей и давлений по живому сечению потока. Для расчетного участка плавно изменяющегося течения реальной жидкости, ограниченного живыми сечениями 1 и 2 , уравнение Бернулли примет следующий вид:

(2)

Где V1 и V2 – средние скорости потока в сечениях 1 и 2 соответственно, м/с; – потери удельной энергии на расчетном участке между сечениями 1 и 2, м; a1 и a2 – коэффициенты кинетической энергии (коэффициенты Кориолиса) в сечениях 1 и 2 соответственно.

Коэффициент кинетической энергии (коэффициент Кориолиса) A, учиты-вающий неравномерность поля скоростей по живому сечению, представляет собой отношение действительного значения кинетической энергии, проносимой потоком жидкости через живое сечение за некоторый отрезок времени, к значению кинетической энергии, определенной для того же отрезка времени при условии, что движение частиц жидкости происходит со средней для данного сечения скоростью

. (3)

Уравнение Бернулли для потока реальной жидкости является Уравнением баланса энергии с учетом потерь. Энергия, теряемая жидкостью, не исчезает бесследно, а превращается в другую форму – Тепловую.

Графической иллюстрацией этих изменений является Напорная линия (н. л.).

Напорная линия – это график изменения (в случае идеальной жидкости – сохранения) полной удельной механической энергии вдоль потока (струйки).

Из Уравнения неразрывности Для элементарной струйки

, (4)

Или для потока реальной несжимаемой жидкости

, (5)

Следует, что скорость (следовательно, удельная кинетическая энергия) изменятся обратно пропорционально площади живого сечения (): увеличивается на суживающихся участках, уменьшается на расширяющихся участках и остается постоянной на участках с постоянным сечением. Изменение кинетической энергии приводит к изменению потенциальной энергии: увеличение кинетической энергии сопровождается уменьшением потенциальной и наоборот. Характер этих изменений иллюстрирует Пьезометрическая линия (пьез. л.).

Пьезометрическая линия – это график изменения Гидростатического напора вдоль потока (струйки).

Описание устройства № 4

Устройства № 4 содержит баки 1 и 2, сообщаемые через опытные каналы переменного № и постоянного 4 сечений (рис.5). Каналы соединены между собой равномерно расположенными пьезометрами I – V, служащими для измерения пьезометрических напоров в характерных сечениях. Устройство заполнено подкрашенной водой. В одном из баков предусмотрена шкала 5 для измерения уровня воды.

При перевертывании устройства благодаря постоянству напора истечения H0 во времени, обеспечивается установившееся движение воды в нижнем канале. Другой канал в это время пропускает воздух, вытесняемый жидкостью из нижнего бака в верхний.

Рис. 5. Схема устройства № 4: 1, 2 – баки; 3, 4 – опытные каналы переменного и постоянного сечений; 5 – уровнемерная шкала; I – V – пьезометры

Порядок выполнения работы

1. Заполнив водой бак 1 (см. рис. 5), перевернуть устройство для получений течения в канале постоянного сечения 4.

2. Снять показания пьезометров по нижним положениям менисков воды в них для пяти сечений I…V, пьезометрический напор в шестом сечении

Равен нулю, то есть .

3. Измерить время T (в секундах) перемещения уровня воды в баке на произвольно заданную величину H.

4. По данным измерений определить:

А) расход жидкости по следующей зависимости

, м3/с, (5)

Числовые значения поперечного сечения бака А и В Определить по табло на устройстве № 4;

Б) среднюю скорость потока в сечениях I…VI (значения площадей сечений W

Приведены на табло устройства № 4)

, м/с ; (6)

В) скоростные напоры В сечениях I…VI, приняв коэффициент кинетической энергии aI…a VI »1;

Г) полные напоры в сечениях канала I…VI, совместив плоскость сравнения с осевой линией потока (таким образом, z I…z VI = 0).

5. Данные опытов занести в табл. 9 (см. Приложение).

6. Построить для данного канала Пьезометрическую линию. Для этого, обозна-чив контуры канала, отложить в масштабе от его осевой линии (плоскости срав-нения) для сечений I…VI пьезометрические напоры . Соединив край-ние точки, получить пьезометрическую линию, иллюстрирующую изменение потенцииальной энергии (гидростатического напора) вдоль потока (рис.6, кривая 1).

7. На том же рисунке построить Напорную линию. Для этого в масштабе отложить для каждого сечения I…VI от пьезометрической линии скоростные напоры (или от осевой линии потока – полные напоры ) и соединить полученные точки (см. рис.6, кривая 2).

Рис. 6. Построение напорных линий для канала постоянного сечения

8. Заполнив водой бак 2 (см. рис. 5) и перевернув устройство для получения течения в канале переменного сечения 3, повторить опыт по п. п. 2…7. Пьезометрическая и напорная линии для данного канала показаны на рис. 7 кривой 1 и 2 соответственно.

9. Сделать выводы по данной работе.