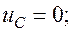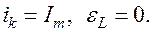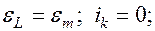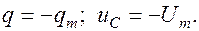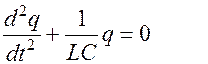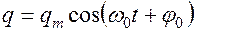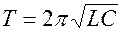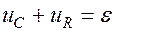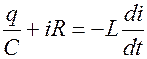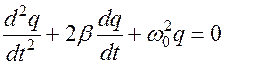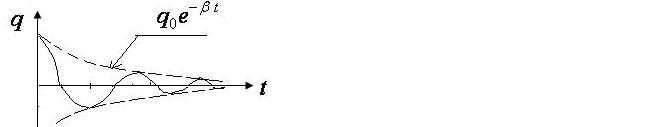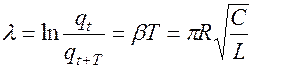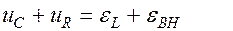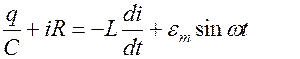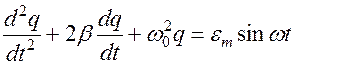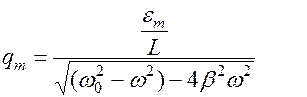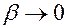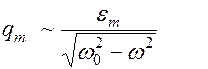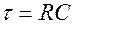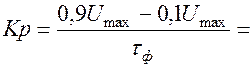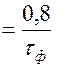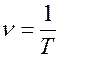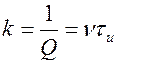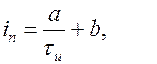Процессы, происходящие в идеальном
Электромагнитные колебания – это колебания величин заряда, силы тока, напряжения, эдс индукции и характеристик переменного электромагнитного поля.

Свободных (собственные) колебания – это ко —
Рис.11.1 лебания, которые совершаются без внешнего воздействия за счет первоначально накопленной энергии.
Рассмотрим идеальный колебательный контур, в котором активное сопротивление 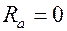

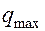
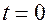
Процесс будем рассматривать в течение одного периода (рис.11.3).
1. При 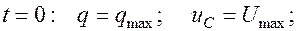
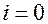
2. В промежуток времени от 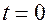
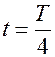
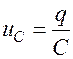
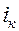
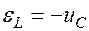
В момент времени 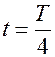
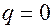

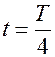
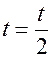
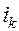
В момент времени
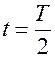
4. В промежутки времени от 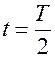
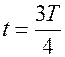
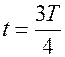
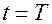
Таким образом, в колебательном контуре возникают электромагнитные колебания – колебания заряда, тока, напряжения и эдс индукции.
Незатухающие электромагнитные колебания.
Такие колебания происходят в идеальном колебательном контуре, в котором 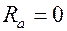
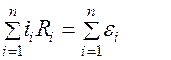
Т.к. 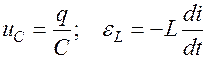
Его решением являются функции
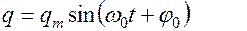
График этой функции, а также графики напряжения, тока и эдс индукции представлены на рис.11.4:
Напряжение на конденсаторе 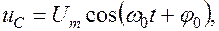
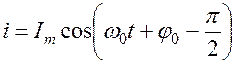
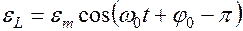
Период колебаний незатухающих колебаний определяется по формуле Томсона:

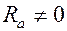
Согласно второму правилу Кирхгофа для данного контура
Дифференциальное уравнение для затухающих колебаний
где 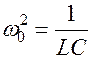
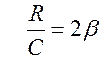
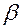
Его решением является функция
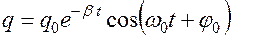
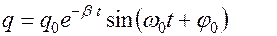
В этих уравнениях величина 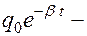
Быстрота затухания колебаний характеризуется логарифмически декрементом затухания
Добротность 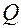
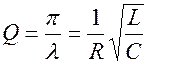
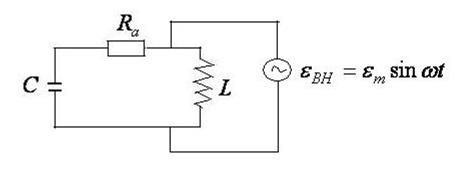
Чтобы колебания в контуре были не затухающими, к нему необходимо подать внешнюю эдс (рис.11.7), которая должна быть периодической и должна иметь частоту колебаний 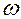
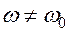
Второе правило Кирхгофа для такого контура запишется в виде
Дифференциальное уравнение вынужденных колебаний
Решением этого уравнения является функция
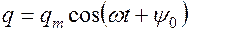
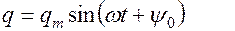
Колебания происходят с частотой внешней эдс. Начальная фаза колебаний меняется на новую фазу 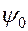
При малых затуханиях, т.е. при
Если 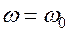
•Идеальный колебательный контур. Процессы, происходящие в нем. •Свободные незатухающие колебания. Дифференциальное уравнение, описывающее их. Решение уравнения. Графики изменения заряда, силы тока, напряжения, ЭДС. Формула Томсона. •Реальный колебательный контур. Затухающие электромагнитные колебания. Дифференциальное уравнение, решение, график. Логарифмический декремент затухания, добротность. •Вынужденные электромагнитные колебания. Дифференциальное уравнение, решение. Резонанс. •Автоколебания. Генератор незатухающих электромагнитных колебаний на примере аппарата УВЧ-терапии.
Апериодический разряд конденсатора

Если заряженный конденсатор отключить от источника напряжения и замкнуть его на сопротивление 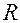
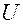
кратковременный импульс тока – ток разрядки конденсатора.
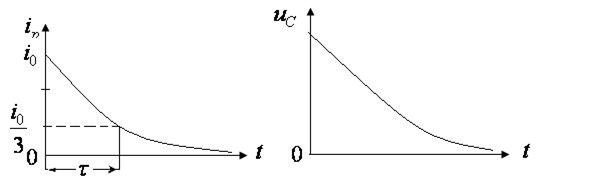
Мгновенные значения тока разрядки определяются по формуле
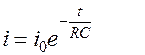
Аналогично изменяется и напряжение на обкладках конденсатора. Графики тока разрядки и напряжения показаны на рис. 12.2

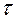
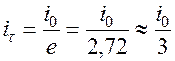
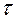
Ток зарядки имеет такую же форму, как и ток разрядки, но течет в противоположном направлении (рис.12.3).
Таким образом, импульсы – это кратковременные изменения силы тока и напряжения.
Импульсный ток – это повторяющиеся во времени импульсы. Они могут быть самой различной формы (рис. 12.4):
Характеристики импульсных токов.
1. Длительность импульса — 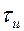
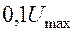
2. Крутизна фронта характеризует скорость нарастания напряжения или силы тока
3. Период 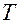
4. Частота повторения импульсов
5. Скважность следования импульсов
6. Коэффициент заполнения
Генераторы импульсных токов.

Рис. 12.6 Рис. 12.7
Неоновая лампа зажигается при определенном напряжении 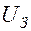
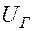
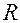
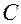
3. 
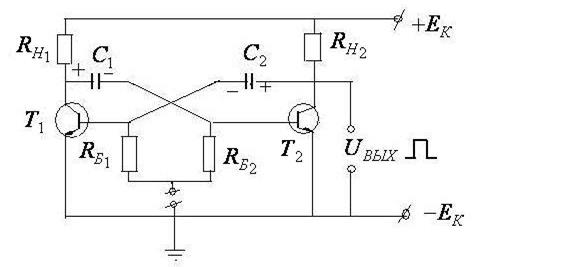
3. Мультивибратор. Схема его представлена на рис.12.10
Мультивибратор содержит два транзистора, два конденсатора и по паре сопротивлений 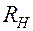
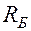
Конденсаторы служат для генерации импульсов (заряжаются от источника постоянного тока 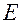
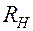
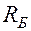
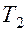
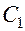
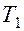
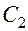
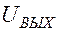
Изменение формы импульса.
После мультивибратора получаются импульсы прямоугольной формы. Но для лечения различных заболеваний используют импульсы различной формы. Чтобы изменить форму импульса, на выходе мультивибратора собирают дифференцирующую (рис. 12.11) или интегрирующую цепь (рис.12.13):
1. Дифференцирующая цепь
Её применяют в том случае, если 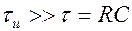
На вход цепочки подается входное напряжение прямоугольной формы. Очевидно,
| Рис. 12.11 | 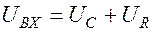 . . |
Выходное напряжение включено параллельно резистору 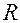
Форму выходного напряжения можно получить при графическом вычитании. На рис. 12.12 а) показан импульс входного напряжения. Затем импульс прекраща-ется, конденсатор разряжается (рис. 12.12 б). Вычитая значения функции, представленной на рис. 12.12 б) из значений функции, представленной на рис. 12.12 а), получаем вид функции выходного напряжения (рис. 12.12 в).
Таким образом, на выходе из цепочки получаются два остроконечных импульса противоположного знака.
Рассмотренная цепочка называется дифференцирующей потому, что выходное напряжение пропорционально производной от входного напряжения 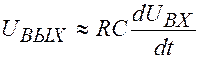
2. Интегрирующая цепь.
Применяется в том случае, если 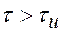

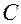
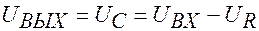
Если на вход цепи подан прямоугольный импульс (рис. 12.14 а), то напряжением на выходе является напряжение на пластинах конденсатора (рис.12.14 б). Конденсатор не успевает зарядиться до 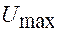

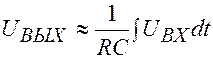
Действие импульсного тока на ткани организма
В основе действия электрического тока на ткани организма лежит движение заряженных частиц, преимущественно ионов тканевых электролитов, в результате чего изменяется обычный состав ионов по обе стороны мембраны, в связи, с чем в клетке происходит ряд биофизических и физиологических процессов, вызывающих её возбуждение . Рис. 12.14
Постоянный ток почти не оказывает раздражающего действия на ткани организма. Раздражение вызывается при изменении силы тока и зависит от скорости, с которой это изменение происходит. Это положение известно как закон Дюбуа-Реймона. Сила тока 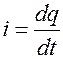
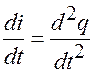
Очевидно, что раздражающее действие зависит от крутизны импульсов.
| Формы импульсных токов | Применение |
Прямоугольные: 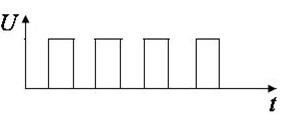 | 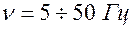 — электросон — электросон 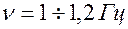 — электрокардиостимуляция — электрокардиостимуляция |
Треугольные: 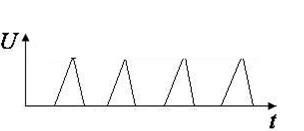 | 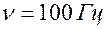 — возбуждение мышц, электрогимнастика — возбуждение мышц, электрогимнастика |
Тетанизирующие: 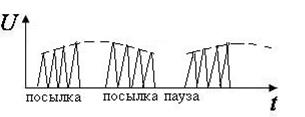 | 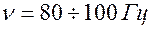 Электростимуляция здоровых мышц Электростимуляция здоровых мышц |
Экспоненциальные: 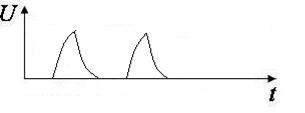 | 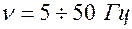 Электростимуляция Электростимуляция |
Экспоненциальные: 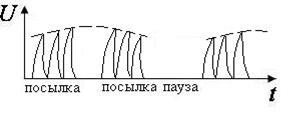 | Электростимуляция пораженных мышц |
Диадинамические: 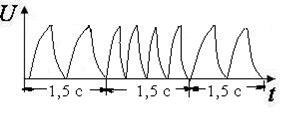 | Электротерапия |
Раздражающее действие прямоугольных импульсов в значительной мере зависит от их длительности 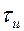
где 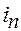
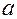
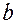
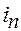
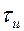


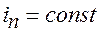
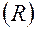
Хронаксия и реобаза характеризуют возбудимость органа и могут служить показателями их функционального состояния или диагностического признака их поражения.
•Апериодический разряд конденсатора. Постоянная времени. •Принцип генерации импульсных токов на примере генератора с неоновой лампой и блокинг-генератора. Мультивибратор. •Электрический импульс и его характеристики. Импульсный ток. •Характеристики импульсных токов.•Изменение формы импульса (дифференцирующая и интегрирующая цепи).•Действие импульсных токов на организм. Закон Дюбуа-Реймона. Формула Вейса-Лапика. •Применение импульсных токов в медицине.
ИМПЕДАНС ТКАНЕЙ ОРГАНИЗМА.
Видео:Колебательный контур | ЕГЭ Физика | Николай НьютонСкачать

Дифференциальное уравнение электромагнитных колебаний в электрическом колебательном контуре
Свободные (собственные) колебания электрического заряда q на обкладках конденсатора и силы J электрического тока в электрическом колебательном контуре возникают, когда предварительно заряженный конденсатор замыкают на катушку с индуктивностью L (рис. 175).
Силу J электрического тока можно считать одинаковой во всех частях контура в каждый момент времени t, если выполняется условие, что электромагнитное поле распространяется в пространстве со скоростью, равной скорости света с в вакууме
где I — линейные размеры контура, с — скорость света в вакууме, v — частота колебаний.
Переменный электрический ток, для которого выполняется данное условие, называют квазистационарным. Колебательный контур можно рассматривать, как разомкнутую электрическую цепь, концами её являются обкладки конденсатора.
Пусть в некоторый момент времени t электрический заряд на обкладках конденсатора равен q (t), а разность потенциалов (
Для участка электрической цепи 1 — L — 2 (рис. 175) запишем закон Ома, согласно которому произведение силы J электрического
тока на электрическое сопротивление R участка цепи равно сумме разности потенциалов (рр/ — 1 — циклическая частота свободных колебаний в контуре.
Согласно уравнению (19.35) сила / электрического тока опережает электрический заряд q по фазе на Д. В момент времени t,
когда сила J электрического тока в контуре максимальна (J = J мах), электрический заряд q на обкладках конденсатора равен нулю (q = 0) и наоборот.
Напряжение U на конденсаторе со временем t изменяется по гармоническому закону, совпадая по фазе с электрическим зарядом q
где U мах = ^ >»‘ амплитуда колебаний напряжения U (разности
Электродвижущая сила самоиндукции ? с, а так же и энергии электрического Wи магнитного IV „а,,„ поля изменяются со временем, совершая гармонические колебания, описываемые формулами
где ? с.мах = Ц мах ю0 2 — L- амплитуда колебаний ЭДС самоиндукции.
Полная энергия W полн, сосредоточенная в колебательном контуре, описывается в любой момент времени t уравнением
Здесь учли, что со0 = 1 и sin (со0-Г + 1 с учётом, что J 2 х = col ? q 2 ,
получим
Максимальные значения энергии электрического поля в конденсаторе достигаются в моменты времени, когда энергия магнитного поля катушки индуктивности равна нулю.
Согласно закону сохранения полной энергии, в колебательном контуре выполняется равенство
или
Итак, колебательный процесс в контуре характеризуется периодическим переходом энергии электрического поля конденсатора в энергию магнитного поля катушки. Полная энергия колебательного контура в моменты времен t = 0, t = Т, t = 2Т и т. д. сосредоточена в
электрическом поле конденсатора, а в моменты времени t = Z. t = 1 Г,
t = 5 т и т. д .в магнитном поле катушки индуктивности. В
колебательном контуре дважды за период Т колебаний происходит перекачка энергии из электрического поля конденсатора в магнитное поле катушки индуктивности и обратно.
В начальный момент времени (t =0) на обкладках заряженного конденсатора размещается максимальный электрический заряд q (q = q лшх) и энергия электрического поля имеет максимальную величину
Сила J электрического тока равна нулю (У = 0).
Сравним параметры свободных механических колебаний пружинного маятника и свободных электромагнитных колебаний в электрическом колебательном контуре (табл.4).
Тело массой m пружинного маятника в начальный момент времени (t =0) максимально удалено от положения равновесия Поэтому потенциальная энергия W упруго деформированной пружины имеет максимальное значение
Энергия электрического поля конденсатора является аналогом потенциальной энергии деформированной пружины пружинного маятника. Сила У электрического тока в колебательном контуре в момент времени t = >_Т достигает максимального значения (У = J мах), 4
энергия магнитного поля в катушке с индуктивностью L максимальна (W = Wмаг мах), а электрический заряд q на обкладках
конденсатора равен нулю (q = 0). Электрический ток не прекращается в контуре за счёт наличия катушки индуктивности и при отсутствии электрического заряда на обкладках.
Тело массой m пружинного маятника, движущееся под действием силы упругости к положению равновесия, в момент времени t = ф Т
проходит его по инерции с максимальной скоростью, имея максимальную кинетическую энергию W мах, равную
Отсюда следует, что энергия магнитного поля катушки индуктивности является аналогом кинетической энергии пружинного маятника, а индуктивность L катушки аналогична массе т тела пружинного маятника.
Величина (J_), обратная ёмкости С конденсатора, аналогична
коэффициенту жёсткости к пружины.
Параметры свободных механических колебаний пружинного маятника и свободных электромагнитных колебаний в электрическом колебательном контуре
Электрический заряд конденсатора q
Скорость движения тела г = ^ х
Сила электрического тока J=dq dt
Скорость изменения силы
Потенциальная энергия упруго деформированной пружины
Энергия электрического поля
Кинетическая энергия движущего тела массы
Энергия магнитного поля катушки индуктивности
Индуктивность катушки L
Коэффициент жёсткости пружины к
Величина, обратная ёмкости конденсатора — 1
Частота собственных колебаний
Частота собственных электромагнитных колебаний
Видео:Урок 353. Колебательный контурСкачать

Лекция № 5 Свободные электромагнитные колебания
СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
Выписка из рабочей программы дисциплины «Колебания и волны» – 010900
2.1 Свободные электромагнитные колебания.
Колебательный контур. Процессы в идеализированном колебательном контуре. Электромагнитные гармонические колебания. Дифференциальное уравнение свободных незатухающих электромагнитных колебаний и его решение. Собственная частота свободных электромагнитных колебаний. Формула Томсона. Закон сохранения и превращения энергии в идеализированном колебательном контуре.
1. Свободные электромагнитные колебания
Электромагнитные колебания представляют собой взаимосвязанные периодические изменения зарядов, токов, характеристик электрического и магнитного полей, сопровождающиеся взаимными превращениями этих полей.
Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур – цепь, состоящая из конденсатора ёмкостью 

Если сопротивление контура 


Пусть в начальный момент времени (








В контуре возникают электромагнитные колебания, при которых происходит превращение энергии электрического поля в энергию магнитного поля и наоборот. Рисунок 2 представляет собой график зависимости заряда конденсатора 



контура (а; б; в; г; д).

Период собственных незатухающих колебаний в колебательном контуре определяется формулой Томсона

а циклическая частота

Колебания заряда происходят по гармоническому закону

где 


 |
На рисунках 3 и 4 представлены соответственно идеальный колебательный контур и график зависимости 

Очевидно, что изменение напряжения между обкладками описывается таким же законом

где 
Так как электрический ток характеризует скорость изменения заряда на обкладках конденсатора,

где 
Из выражений (7), (8), (9) следует, что колебания заряда (напряжения) и тока в контуре сдвинуты по фазе на 
Идеальный колебательный контур (рис. 3), в котором происходят свободные незатухающие электромагнитные колебания, представляет собой электрическую цепь, состоящую из конденсатора емкостью 

В контуре действует только одна э. д.с. – э. д.с. самоиндукции, следовательно

где 


Так как 



где 
Уравнение колебаний принимает вид
и называется уравнением свободных незатухающих электромагнитных колебаний в дифференциальной форме.
Из математики известно, что решение этого уравнения имеет вид

т. е. соответствует формуле (7) и рис. 4 (при 
Таким образом, свободные незатухающие электромагнитные колебания являются гармоническими, а их период определяется формулой Томсона:
2. Закон сохранения и превращения энергии в идеализированном колебательном контуре
Исключительно важным является вопрос об энергии гармонических колебаний. С энергетической точки зрения гармоническое колебание представляет собой непрерывный процесс перехода кинетической энергии движущихся частей осциллятора в потенциальную энергию упругого элемента. Полная энергия гармонического осциллятора есть величина постоянная, так как для него потерь нет. Она равна либо максимальной кинетической энергии ( в момент прохождения положения равновесия) , либо максимальной потенциальной энергии (при амплитудном смешении). В задачах используются именно эти энергии, так как с их помощью можно оценить величину амплитуды и частоты собственных колебаний осциллятора.
Расчет энергии W гармонического осциллятора осуществляют стандартным образом. Для механических осцилляторов:
🎥 Видео
Свободные электромагнитные колебания. 11 класс.Скачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Физика 11 класс (Урок№7 - Свободные и вынужденные электромагнитные колебания. Колебательный контур.)Скачать

ЕГЭ2020. ФИЗИКА. Электромагнитные колебания и колебательный контурСкачать

Колебательный контурСкачать

Дифференциальные уравнения. 11 класс.Скачать

Затухающие колебания Лекция 11-1Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Принцип работы колебательного контураСкачать

Однородное дифференциальное уравнениеСкачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Урок 354. Математическое описание процессов в колебательном контуреСкачать

4. Однородные дифференциальные уравнения (часть 1)Скачать

Тема 8. Колебательный контур. Свободные электромагнитные колебания в контуре. Формула ТомсонаСкачать