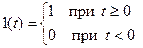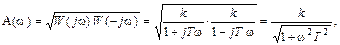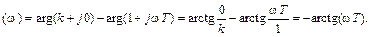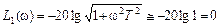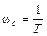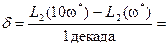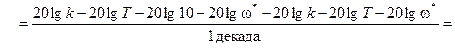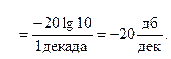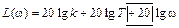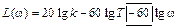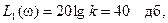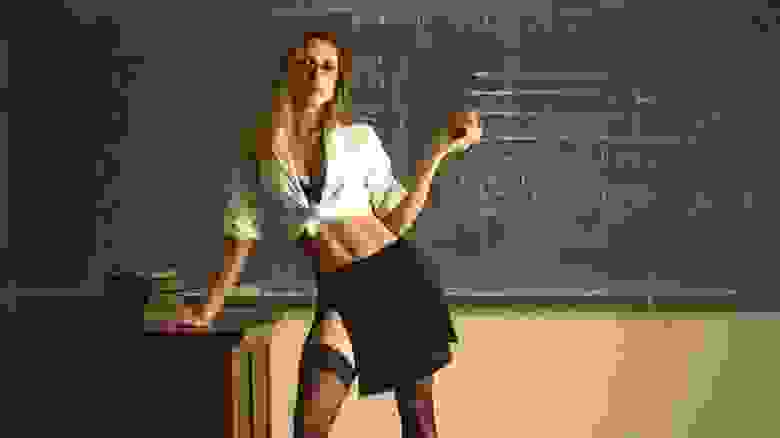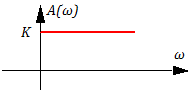Идеальное усилительное безынерционное звено описывается уравнением (7 видео)

Усилительное звено.

Самым простейшим звеном является безынерционное звено, которое не только в статическом, но и динамическом режиме описывается алгебраическим уравнением.

Предполагается, что передача сигнала от входа к выходу производится мгновенно без какой либо инерции. Поэтому такое звено называют безынерционным. Примерами таких звеньев являются механический редуктор, безинерционный операционный усилитель, делитель напряжения, рычажная передача и т.п.

После применения к алгебраическому уравнению (1) преобразования Лапласа

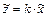
получим передаточную функцию звена

. (2.2)

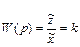
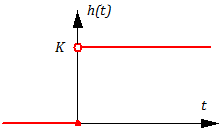
Рассмотрим сначала временные характеристики безынерционного звена. Как уже говорилось в п.2., переходная функция звена h(t) есть его реакция на единичный скачек 1(t),поэтому согласно п.2.

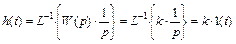
В выражениях для переходных характеристик h(t) имеется сомножитель

Этот сомножитель вводится для того, чтобы подчеркнуть, что h(t), является следствием приложения ко входу звена в момент времени t = 0 единичного скачка 1(t), может существовать (не быть равной нулю) только при t ≥0. Для моментов времени t

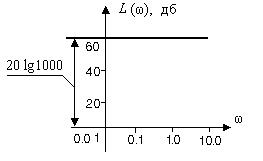
Рис. 2.5. ЛАЧХ безынерционного звена для k =1000

Инерционное звено.

Звено называется инерционным, если связь между входным х(t) и выходным z(t) сигналами звена определяется дифференциальным уравнением:

. (2.4)

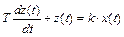
Смысл коэффициентов T и k будет пояснен позже. Такое звено называют также апериодическим, статистическим, одноемкостным, релаксационным.

Надо заметить, что этот тип звена наиболее часто встречается в практике автоматического управления. В качестве примеров инерционного звена можно назвать термопару, магнитный усилитель, двигатель постоянного тока с независимым возбуждением, генератор и т.д.

Если к (2.4) применить преобразование Лапласа, при нулевых начальных условиях, то получится

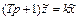
Найдем отсюда передаточную функцию звена

. (2.5)

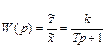
Переходная характеристика звена определиться из выражения

(2.6)

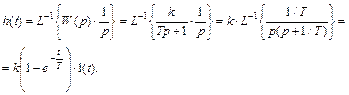
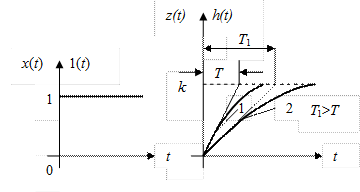
На рисунке 2.6 представлены для сравнения сигналы х(t) = 1(t) и z(t) = h(t) инерционного звена.

Рис. 2.6. Единичный скачок и переходная

функция инерционного звена.

Из рисунка видно, что, сравнивая установившиеся значение выходного сигнала звена k и величину входного 1(t), можно сделать вывод, что параметр k в (2) есть коэффициент усиления звена. Из этого же рис. 20. видно, что кривая 2 характеризует более замедленную, более инертную реакцию звена на единичный скачок. Для кривой 2 параметр Т₁ (смысл которого ясен из рисунка) больше параметра Т₂ для кривой 1.Значит, этот параметр может служить мерой инерционности звена. Обычно, этот коэффициент Т называют постоянной времени звена.

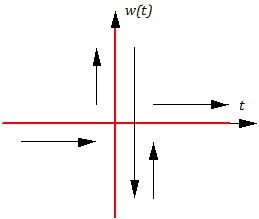
Импульсная переходная (весовая) функция звена w(t), представленная на рис. 2.7, определяется следующим образом

. (2.7)

Получим частотную передаточную функцию звена W(jω), заменив в (2.5) р на jω

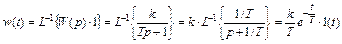
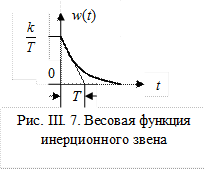
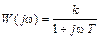
Отсюда легко определяются АЧХ A(ω) и ФЧХ φ(ω)

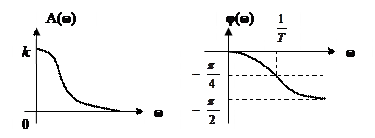
Качественный вид графиков, соответствующих выше найденным зависимостям A(ω) и φ(ω), представлен на рис. 2.8.

Рис.2.8. АЧХ и ФЧХ инерционного звена.

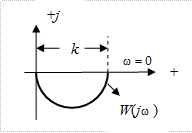
По найденным графикам A(ω) и φ(ω) на рис. 2.9 построена амплитудно-фазовая характеристика инерционного звена

Рис. 2.9. АФХ инерционного звена.

Из выражения для АЧХ звена выводится точное соотношение для ЛАЧХ:

. (2.8)

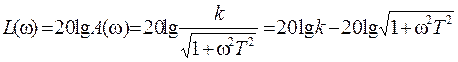
В выражении для L(ω) вычислять слагаемое 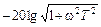для различных частот от 0 до ∞ представляет определенные неудобства. Вот если бы удалось диапазон частот 0 ≤ ω 2 T 2 можно пренебречь по сравнению с первым

Итак, первая асимптота представляет собой прямую линию, не зависящую от частоты, и проходящую по оси частот. Наклон такой асимптоты равен 0.

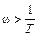
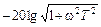
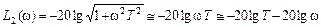
На втором участке рассмотрим диапазон частот, для которого или ωT >1. Тогда асимптота второго участка может быть получена, если в выражении пренебречь первым слагаемым подкоренного выражения по сравнению со вторым

. (2.9)

Поскольку при построении ЛАЧХ по оси абсцисс частоты откладываются в логарифмическом масштабе, то вторая асимптота представляет собой уравнение прямой, зависящей от частоты ω (т.е. проходящей с некоторым наклоном к оси частот). Ниже будет показано, как определять наклон таких асимптот.

Когда же сопрягаются, т.е. становятся равными эти две асимптоты L₁(ω) и L₂(ω)? Очевидно, тогда, когда первое слагаемое подкоренного выражения точной кривой 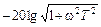становится равным второму

Отсюда частота, при которой сопрягаются обе асимптоты, или сопрягающая частота

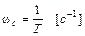
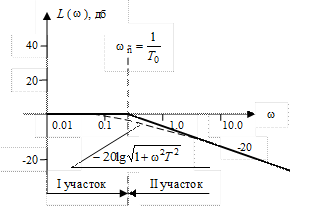
Асимптоты L₁(ω) и L₂(ω) представляют собой совокупность прямых, приблизительно заменяющих точную кривую 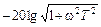(рис.23). На этом рисунке помимо асимптот L₁(ω) и L₂(ω) пунктиром показана и упомянутая точная кривая.

Рис. 2.10. Точная ЛАЧХ 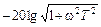и ее асимптоты.

Вернемся к выражению (2.8) для точной ЛАЧХ звена и построим асимптоты, приблизительно ее заменяющие.

Начинать построение ЛАЧХ рекомендуется с определения сопрягающих частот. Сопрягающих частот у ЛАЧХ будет столько, сколько звено (или САР) имеет постоянных времени. В случае инерционного звена из рис. 2.10 видно, что имеется лишь одна постоянная времени Т и, значит, одна сопрягающая частота

Эта сопрягающая частота делит ось частот на два участка ω ω_c. Для более сложных звеньев или САР число постоянных времени может достигать произвольного значения m, тогда число участков будет m+1.

В случае инерционного звена рассмотрим:

или ω T 1.

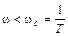
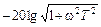
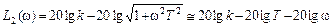
Выражение для асимптоты II участка получается аналогично предыдущему случаю, только учитывать надо условие (6) и в члене следует пренебречь первым слагаемым по сравнению со вторым

Как уже говорилось выше, с учетом логарифмического масштаба по оси частот данное выражение представляет собой прямую линию, имеющий некоторый наклон к оси абсцисс. Чтобы провести эту асимптоту на графике, необходимо знать ее наклон и точку, через которую проходит данная прямая. Что касается упомянутой точки, то найти ее легко, если понять, что конец предыдущей асимптоты является началом следующей. В самом деле, если взять конец первой асимптоты, т.е. ее значение при

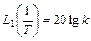
и начало второй асимптоты, т.е. опять же ее значение при

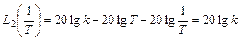
то подтверждается вышеприведенное утверждение

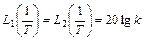
Для определения наклона асимптоты к оси абсцисс найдем для частоты ω * , относящейся ко II участку

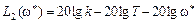
Затем увеличим частоту ω * в 10 раз (т.е. на декаду) и получим значение L₂(10 ω * )

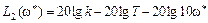
Легко понять, что если взять приращение ЛАЧХ

и отнести его к интервалу изменения частоты, то тем самым определиться наклон асимптоты к оси частот

Итак, наклон второй асимптоты L₂(ω) составляет 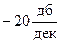, т.е. при росте частоты на 1 декаду L₂(ω) уменьшается на 20 дб.

Вообще же, чтобы не определять каждый раз подобным способом наклоны произвольной асимптоты полезно запомнить следующее правило, наклон асимптоты к оси частот определяется коэффициентом со знаком, стоящим при члене lg ω в выражении для асимптоты. Например, если

то соответствующий наклон равен 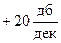, а при

этот наклон будет .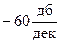

На рис. 24 изображена ЛАЧХ инерционного звена своими асимптотами

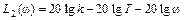
Часто ЛАЧХ звена или системы характеризуют путем обозначения наклонов ее асимптот. В данном случае эта характеристика будет выглядеть так

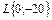
Рис.2.11. ЛАЧХ инерционного звена.

На этом же рисунке пунктиром изображена точная ЛАЧХ L(ω). Видно, что максимальная ошибка, возникающая от замены точной ЛАЧХ на асимптотическую, наблюдается на сопрягающей частоте 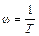и приблизительно равна 3,03 дб.

Чтобы оценить влияние параметров звена k и T на его ЛАЧХ, надо понять, что изменение k приводить к изменению 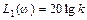. Иными словами, при изменении k первая асимптота перемещается по вертикали параллельно самой себе. Но так как конец первой асимптоты является началом второй, т.е. первая и вторая асимптоты жестко связаны, то точно такое же перемещение по вертикали будет претерпевать и вся асимптотическая ЛАЧХ.

Понятно так же, что при изменении Т меняется сопрягающая частота 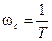. Значит, при изменении T ЛАЧХ инерционного звена будет перемещаться по горизонтали параллельно самой себе.

Содержание

Уравнения и характеристики типовых звеньев АИС
3. Частотные характеристики звеньев и систем автоматического управления. ч. 3.2 Простейшие типовые звенья
3.2.1. Идеальное усилительное звено
3.2.2. Идеальное дифференцирующее звено
3.2.3. Идеальное интегрирующее звено
Пример интегрирующего и дифференцирующего звена на основе конденсатора
📽️ Видео

Видео:10) ТАУ для чайников Части 4.1. и 4.2. Типовые динамические звенья. Усилитель. Апериодическое звено.Скачать

Уравнения и характеристики типовых звеньев АИС

К типовым звеньям АИС относятся простейшие звенья, которые имеют уравнения не выше второго порядка.

Безынерционное (усилительное) звено осуществляет наиболее простое преобразование входной величины — усиление без запаздывания. Его уравнение имеет вид:

где k – постоянная величина ( коэффициент усиления).

Чтобы выяснить свойства безынерционного звена, применим операторный метод и запишем уравнение (1.7) в изображениях

Передаточная функция звена

Отсюда h(t)=k, т.е. переходная характеристика безынерционного звена есть прямая линия (рис. 1.10,а).

Используя соотношение (1.6), получаем комплексный коэффициент усиления

Из выражения (1.8) следует, что график амплитудо-фазовой характеристики (АФХ) безынерционного звена есть точка на действительной оси на расстоянии k от начала координат (рис.1.10,б). На рис.1.10, в приведена фазо-частотная характеристика (ФЧХ) =0 безынерционного звена.

Инерционное (апериодическое) звено описывается дифференциальным уравнением первого порядка

и характеризуется двумя числовыми величинами:

k — коэффициентом усиления, который определяет статические свойства звена, т.е. величину уС, в статическом режиме ;

— постоянной времени, которая определяет длительность переходного процесса (инерционность) звена.

Уравнение (1.9) в изображениях при нулевых начальных условиях имеет вид:

Отсюда получаем передаточную и переходную функцию инерционного звена

Оригинал h(t) будет иметь вид:

т.е. переходная характеристика инерционного звена есть возрастающая экспонента (рис.1.11,а). Величина определяется геометрически как проекция касательной в любой точке экспоненты. За время  выходная величина достигает 63% своего конечного значения. Время переходного процесса принимается равным 3.

Произведя замену р = j в (1.10), получаем комплексный коэффициент усиления инерционного звена

Из выражения (1.11) определяется модуль А и аргумент :

На рис.1.11,б приведена АФХ инерционного звена, построенная по выражениям (1.12) при изменении  от 0 до . Она представляет собой полуокружность в четвертом квадранте с центром, расположенным на действительной оси на расстоянии R= k/2 от начала координат. Из графика АФХ видно, что инерционное звено является фильтром низких частот. За полосу пропускания звена принято считать диапазон частот

когда коэффициент усиления изменяется от k до . При . На рис.1.11,в приведена ФЧХ инерционного звена.

Колебательное звено описывается дифференциальным уравнением второго порядка

От вида корней характеристического уравнения

зависит характер переходного процесса может быть колебательным затухающим (корни комплексно-сопряжённые, рис.1.12,а), колебательным незатухающим (корни чисто мнимые, рис.1.12, б) и апериодическим (корни вещественные, рис. 1.12, в).

При нулевых начальных условиях уравнение (1.13) в изображениях имеет вид:

Из уравнения (1.14) находим передаточную и переходную функцию колебательного звена

и комплексный коэффициент усиления

На рис.1.12,г показана АФХ колебательного звена. При в работе звена может наблюдаться резонанс, когда коэффициент усиления амплитуды больше статического коэффициента k. При На рис.1.12,д приведена ФЧХ колебательного звена.

Дифференцирующе звено даёт на выходе величину, пропорциональную производной от входной величины.

Идеальное дифференцирующее звено описывается уравнением

или в изображениях при нулевых начальных условиях

Из уравнения (1.15) следует:

График переходной характеристики имеет вид мгновенного импульса (рис.1.13,а) с амплитудой равной бесконечности. Если на вход идеального дифференцирующего звена подана синусоида, то на выходе сигнал будет изменяться по косинусоиде (рис.1.13,б).

Из выражения (1.16) получаем комплексный коэффициент усиления идеального дифференцирующего звена:

АФК совпадает с положительной мнимой полуосью, так как и (рис.1.13,в).

Реальное дифференцирующее звено описывается уравнением

или в изображениях при нулевых начальных условиях

Передаточная и переходная функции звена

Переходная характеристика приведена на рис.1.14, а. Реальные дифференцирующие звенья дают на выходе производную с некоторым искажением, которое заключается в том, что амплитуда выходного импульса конечна, а сдвиг по фазе не равен точно 900 (рис.1.14,в).

Из выражения (1.17) получаем комплексный коэффициент усиления реального дифференцирующего звена

АФХ имеет вид полуокружности в первом квадранте (рис.1.14,б). Таким образом, инерционность реального звена уменьшает опережение по фазе тем больше, чем выше угловая частота , что также видно из графика ФЧХ (рис.1.14,б).

Идеальное интегрирующее звено описывается уравнением

или в интегральной форме

т.е. выходная величина пропорциональна интегралу по времени от входной величины.

Уравнение (1.18) в изображениях имеет вид

тогда изображение передаточной и переходной функции

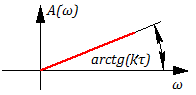
Согласно (1.21) переходная характеристика есть прямая линия с углом наклона  = arctg k (рис.1.15,а), ординаты которой при данном t равны площади под кривой х(t), т. е. значению интеграла (1.19). В качестве интегрирующего часто используют инерционное звено, которое выполняет интегрирование на прямолинейном участке экспоненты (см. рис.1.11,а). При этом, чем больше постоянная времени , тем с большей точностью выполняется интегрирование.

Из выражения (1.20) получаем комплексный коэффициент усиления интегрирующего звена:

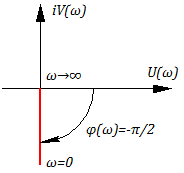
Так как и , то АФХ совпадает с отрицательной мнимой полуосью (рис.1.15, б), т.е. в идеальном интегрирующем звене выходные колебания отстают по фазе от входных на угол 90° (рис. 1.15, в).

Видео:Типовые динамические звенья | Вечер с теорией управления, вебинар 3Скачать

3. Частотные характеристики звеньев и систем автоматического управления. ч. 3.2 Простейшие типовые звенья

Лекции по курсу «Управление Техническими Системами» читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки» факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность!

Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

Тема сегодняшней статьи:
3.2. Типовые звенья систем автоматического управления (регулирования). Классификация типовых звеньев. Простейшие типовые звенья.

Хочешь вкусить плодов познания? — Грызи гранит науки!

Понятие “типовые звенья” в теории управления техническими системами, в основном, связано с описанием САУ (САР) в переменных “вход – выход”, т.е. описание систем в передаточных функциях. Любую линейную САУ (САР) или линеаризованную САР можно структурно расчленить на простейшие элементы (звенья), соединенные между собой соответствующими последовательными, параллельными связями, местными и локальными обратными связями, сумматорами, сравнивающими устройствами и т.д.

Достигнуто общепринятое соглашение, что наиболее удобно расчленять структурную схему САР на звенья 1-го и 2-го порядков. Принято называть такие простейшие звенья типовыми.

С другой стороны, реальная линеаризованная (линейная) система состоит из набора отдельных узлов и агрегатов, соединенных соответствующими связями, причем порядок уравнений динамики вышеуказанных узлов и агрегатов может быть и выше второго. В этом случае звенья (узлы и агрегаты) САР можно классифицировать по их свойствам.

Различают 3 типа звеньев:

Существуют также особые звенья, которые будут рассмотрены позднее.

Учитывая, что передаточная функция линейного (линеаризованного) звена может быть записана как:

где: и — полиномы по степеням s, причем коэффициенты при низшей степени s в полиномах , равны 1, классификацию на типы звеньев можно объяснить видом полиномов или (что эквивалентно) видом коэффициентов в соответствующих уравнениях динамики звена.
Подробнее о передаточной функции см. здесь.

Позиционным звеном считают звено, в котором полиномы N(s) и L(s) содержат свободные члены (равные 1). Например:

или в уравнении динамики (x(t) – входной сигнал, y(t) – выходной):

Из типовых звеньев (1-го и 2-го порядка) к позиционным звеньям относятся: идеальное усилительное звено, апериодические звенья 1-го и 2-го порядка, колебательное звено и форсирующее звено.

Дифференцирующим звеном считается звено, в котором полином L(s) содержит свободный член (равный 1), а полином N(s) не содержит свободного члена ().
Например:

или в уравнении динамики:

Из типовых звеньев к дифференцирующим звеньям относятся идеальное дифференцирующее звено, инерционно-дифференцирующее звено.

Интегрирующим звеном считается звено, в котором полином N(s) содержит свободный член (), а полином L(s), не содержит свободного члена (). Например:

или в уравнении динамики:

Из типовых звеньев к интегрирующим звеньям относятся идеальное интегрирующее звено, инерционно–интегрирующее звено.

Пример переходного процесса при единичном ступенчатом воздействии на три разных звена, приведенных выше:

3.2.1. Идеальное усилительное звено

Уравнение динамики каждого звена имеет вид: , т.е. уравнение не является дифференциальным, следовательно, данное звено является безынерционным.

Переходя к изображениям , получаем:
– уравнение динамики звена в изображениях.
Передаточная функция идеального усилительного звена:

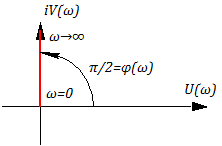
АФЧХ не зависит от ω, поскольку:

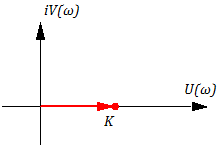
Рисунок 3.2.1 АФЧХ идеального усилительного звена

Годограф АФЧХ “вырождается” в точку: U(ω) =K; V(ω) =0;
A(ω) ≡modW(iω) =│W(iω)│=K =>
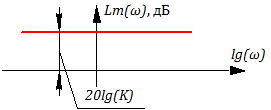
Lm(ω)=20lgA(ω) =20lgK; =>
φ(ω) = const = 0 т.е. фазового сдвига нет. Следовательно, данное звено является безынерционным, чисто усилительным звеном.

Рисунок 3.2.4 ЛАХ идеального усилительного звена

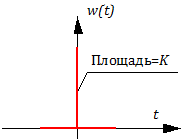
Найдем весовую w(t) и переходную h(t) функции звена (подробнее см. здесь).
Весовая функция:

3.2.2. Идеальное дифференцирующее звено

Уравнение динамики звена имеет вид:

где: – постоянная времени.

Переходя к изображениям:

Уравнение динамики звена в изображениях:

Передаточная функция идеального дифференцирующего звена:

Графики годографа АФЧХ, A(ω) и φ(ω) имеют вид:

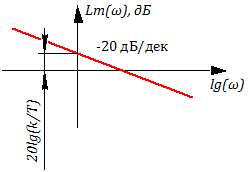
Логарифмическая амплитудная характеристика ЛАХ::

Из рисунка 3.2.9 видно, что данное звено обеспечивает опережение по фазе на /2 (при любой частоте входного сигнала).

Чем выше частота единичного гармонического сигнала на входе в звено, тем выше амплитуда выходного сигнала в установившемся режиме.

Найдем весовую функцию звена:

Учитывая, что δ(t) имеет вид как на рис.3.2.11 (зависимость показана утрированно), а весовая функция пропорциональна производной от δ(t):

Найдем переходную функцию звена:

Иногда идеальное дифференцирующее звено представляется в виде или . В последнем варианте коэффициент К имеет смысл постоянной времени.

3.2.3. Идеальное интегрирующее звено

Уравнение динамики такого звена имеет вид:

или в изображениях:

Передаточная функция идеального интегрирующего звена:

Умножая числитель и знаменатель на i, получаем:

Годограф АФЧХ имеет вид:

Данное звено всегда дает отставание по фазе на угол .

Найдем весовую функцию звена:

Найдем переходную функцию звена:

Примерами устройств, близких к идеальному усилительному звену, можно считать: широкополосный электронный усилитель (приближенно), механический редуктор без учета инерционности и нелинейных эффектов, жесткую механическую муфту и т.д.

Примером идеального дифференцирующего звена можно считать тахогенератор:

где u(t) – напряжение на клеммах тахогенератора, φ(t) – угол поворота якоря (ротора) тахогенератора.

Примером идеального интегрирующего звена можно считать большинство электродвигателей (без учета инерционности якоря), где входным воздействием считать напряжение в обмотке возбудителя (двигателем постоянного тока), а выходным воздействием – угол поворота выходного вала.

Пример интегрирующего и дифференцирующего звена на основе конденсатора

Один и тот же технический элемент, с точки зрения теории автоматического управления, может выступать как в качестве интегрирующего, так и в качестве дифференцирующего звена.

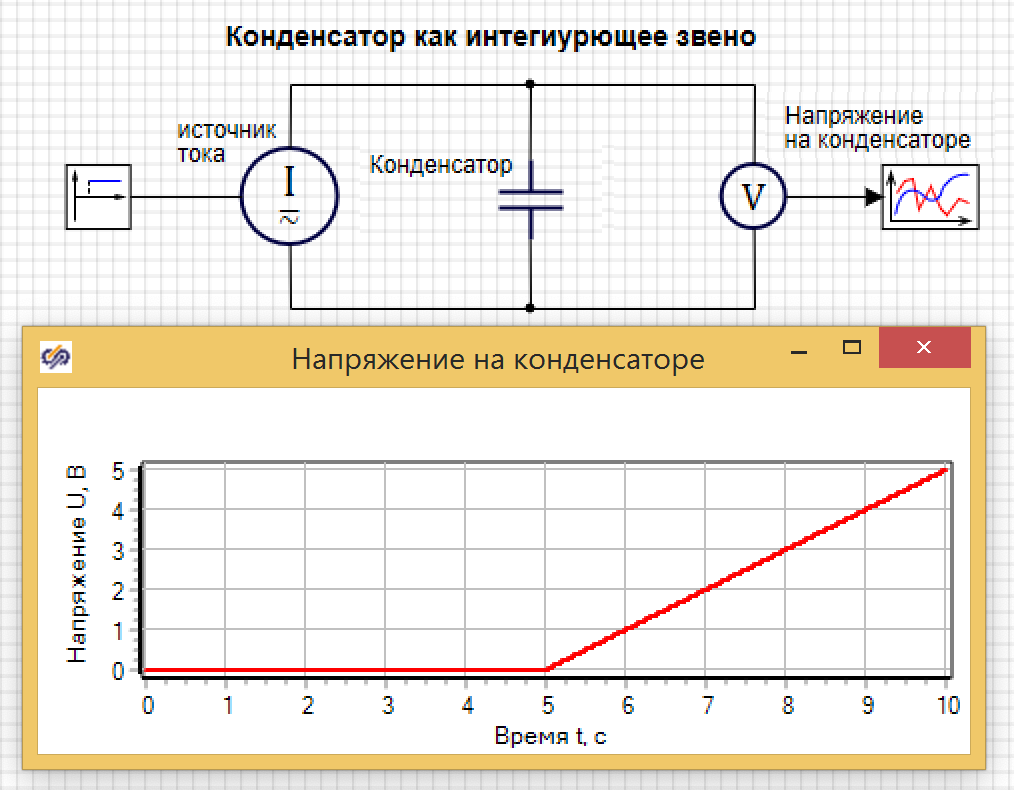
В качестве примера интегрирующего звена можно рассмотреть конденсатор, где входным воздействием является ток, а выходным результатом является напряжение на клеммах конденсатора. Действительно, при малом токе и большой емкости конденсатора, в случае ступенчатого изменения тока с 0, мы получаем график напряжения, совпадающий по форме с переходной функцией интегрирующего звена. На рисунке 3.2.20 представлена такая модель, где ток ступенькой меняется на пятой секунде расчета.

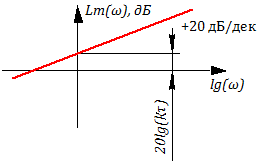
Если построить с помощью гармонического анализатора ЛАХ и ФЧХ, мы увидим, что угол наклона ЛАХ составляет -20 dB/dec, а угол сдвига фазы равен — или -90 градусов на графике (см. рис. 3.2.21).

Тот же самый конденсатор, при определенных параметрах сети, может выступать в качестве идеального дифференцирующего звена, если в качестве входного воздействия подавать напряжение, а в качестве результирующей величины использовать ток в цепи.

Электрическая схема использования конденсатора в качестве дифференцирующего звена с гармоническим анализатором приведена на рисунке 3.2.22. На графиках гармонического анализатора видно, что угол наклона ЛАХ составляет 20 dB/dec, а угол сдвига фазы равен или 90 градусов на графике.