В замкнутой САР (рис. IV. 27) заданы (в числовом выражении)
Рис. IV. 27. Функциональная схема замкнутой САР
Определить устойчивость разомкнутой и замкнутой САР и найти kгр.
Для решения поставленной задачи воспользуемся критерием Гурвица. Найдем передаточные функции, а затем и характеристические уравнения разомкнутой и замкнутой систем.
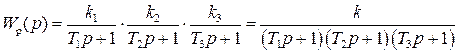
где 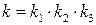
Для разомкнутой системы характеристическое уравнение имеет вид
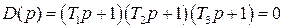
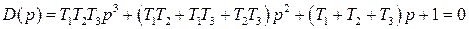
а для замкнутой САР получается
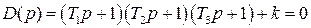
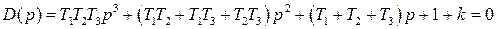
Нетрудно понять, что для исследования устойчивости разомкнутой САР применять критерий устойчивости Гурвица излишне, ибо непосредственно из вида характеристического уравнения разомкнутой системы (IV. 3. 11) легко найти, что все корни левые
т. е. разомкнутая САР при всегда положительных Т1, Т2, Т3 устойчива.
Вот по виду характеристического уравнения замкнутой САР (IV. 3. 12) так просто, как в предыдущем случае, определить соответствующие корни не удается, поэтому приходится применить критерий устойчивости Гурвица . При введении обозначений
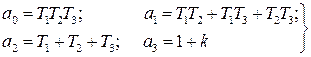
характеристическое уравнение замкнутой САР (IV. 3. 13) примет вид
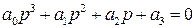
В разделе IV. 2. 2 было выяснено, что для САР с характеристическим уравнением третьего порядка для устойчивости необходимо и достаточно при положительных коэффициентах ai( i =0, 1, 2,3) выполнение условия ( IV. 2. 3)
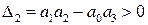
Из (IV. 3. 14) видно, условия ai>0 при положительных Т1, Т2, Т3 и k всегда выполняются, а для проверки условия (IV. 2.3) надо в него подставить заданные значения параметров Т1, Т2, Т3 и k и определить знак минора
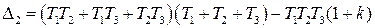
Если этот минор больше нуля, то заданная замкнутая САР устойчива.
Граничный коэффициент усиления kгр найдется из предпоследнего минора, приравненного к нулю
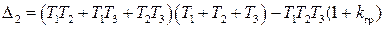
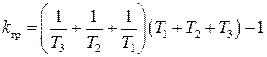
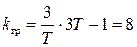
Характеристическое уравнение САР имеет вид
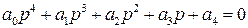
Определить устойчивость САР.
Так как заданное характеристическое уравнение 4-го порядка имеет один неположительный коэффициент (а4=0), то, согласно условию Стодолы (что в данном случае совпадает с критерием Гурвица) САР не сожжет быть устойчивой, а только либо нейтральной либо неустойчивой.
Запишем заданное характеристическое уравнение в другом виде
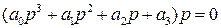
Видно, что один из корней – нулевой. САР будет находиться на границе устойчивости, если все остальные корни характеристического уравнения левые (при наличии хотя бы одного правого корня САР будет неустойчивой). Эти остальные корни будут левыми, если выполняются условия устойчивости для уравнения
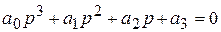
а именно (согласно разделу IV. 2. 2)
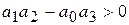
После подстановки значений коэффициентов последнее неравенство
не выполняется, следовательно САР неустойчива.
Передаточная функция разомкнутой САР имеет вид
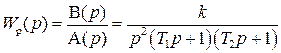
Определить устойчивость замкнутой САР.
Характеристическое уравнение замкнутой САР определяется выражением
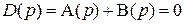
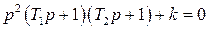
После простого преобразования получим
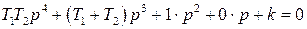
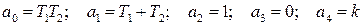
Согласно критерию Гурвица для устойчивости системы необходимо, чтобы все ai( i=0, 1, 2, 3, 4) > 0. В нашем же случае 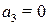
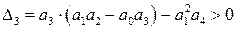
Учитывая что 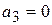
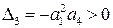
Поскольку 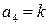
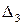
Переходная функция разомкнутой САР имеет вид
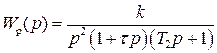
где 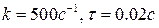
Определить постоянную времени Тгр, при которой замкнутая САР находиться на границе устойчивости.
Получим характеристическое уравнение замкнутой САР
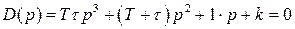
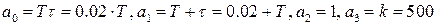
Граница устойчивости определяется из равенства нулю второго минора
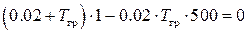
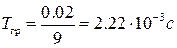
Характеристический полином САР 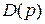
Каково изменение аргумента 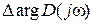
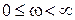
Характеристическое уравнение 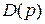
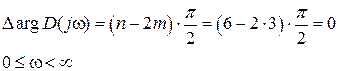
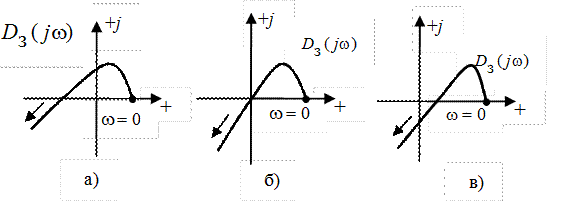
Какой из указанных годографов Михайлова замкнутой системы
Рис. IV. 28. Годографы Михайлова для устойчивой, нейтральной и неустойчивой замкнутой систем.
соответствует САР с передаточной функцией
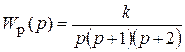
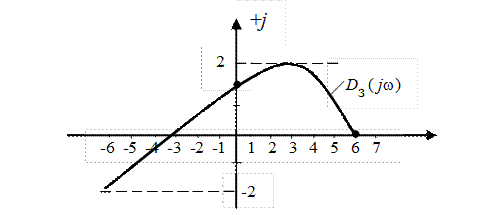
Характеристический полином замкнутой системы имеет вид
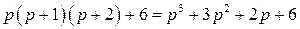
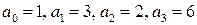
Для этого полинома второй минор оказывается равный нулю
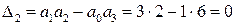
т.е. замкнутая САР находится на границе устойчивости, что соответствует годографу Михайлова, имеющему вид рис. IV. 28, б.
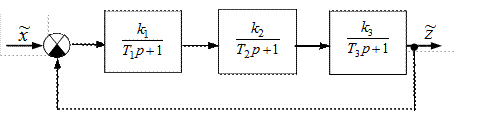
Определить устойчивость разомкнутой и замкнутой САР и найти kгр.
Запишем передаточные функции разомкнутой
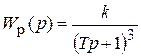
а замкнутой САР
Поскольку из характеристического уравнения разомкнутой САР
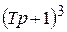
следует, что все три его корня
при положительном Т есть левые, то, значит, разомкнутая САР устойчива.
Для определения устойчивости замкнутой САР применим критерий Михайлова.
Характеристический полином замкнутой системы, имеющий третий порядок,
после замены 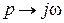
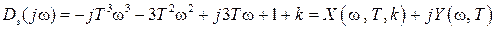
В этом выражении мы выделили действительную часть 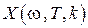
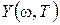
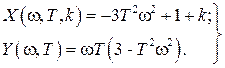
Ответ на вопрос – устойчива ли замкнутая САР можно получить по виду годографа Михайлова, зависящего от конкретных значений параметров k и T. Пусть для определенности k =5, T =1 с. Тогда соотношения (IV. 3. 15) примут
Задаваясь численными значениями 
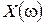
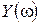

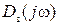
 | 1.42 | 1.5 | 1.73 | ∞ |
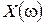 | -0.75 | -3 | -6 | ∞ |
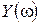 | 1.42 | 1.125 | -2 | ∞ |
Рис. IV. 29. Годограф Михайлова.
Поскольку годограф Михайлова, начинается на положительном отрезке действительной оси, с ростом частоты от 0 до 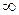
Определим теперь kгр. В разделе IV. 3. 2 было показано, что на границе устойчивости годограф Михайлова проходит через начало координат, т.е. выполняются условия (IV. 3. 4) .
В нашем случае при k = kгр, 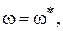
Из второго из этих уравнений, отбрасывая неверное решение 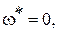
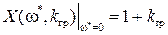
Подставляя это значение граничной частоты в выражение для 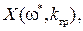
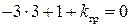
т.е. kгр = 8, как и в примере П. IV. 1.
П. IV. 8. Предыдущую задачу П. IV. 7. решить с помощью критерия Найквиста.
Передаточную функцию разомкнутой системы мы получили в виде
откуда ясно, что все корни характеристического уравнения левые и, значит, разомкнутая система устойчива.
Если провести замену 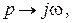
Построим эту характеристику. Найдем сначала 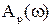
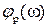
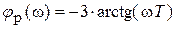
При
При
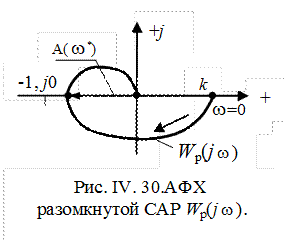
Следовательно, качественно АФХ разомкнутой системы Wp(j 
Устойчивость системы в замкнутом состоянии зависит от того, охватывает ли 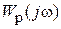




Из заданной операторной формы управления системы получим
Wp(j 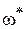
В отличии от предыдущего примера для разнообразия АФХ разомкнутой САР Ap( 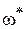
Wp(j 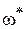
Для этого нужно освободиться от мнимости в знаменателе выражения для
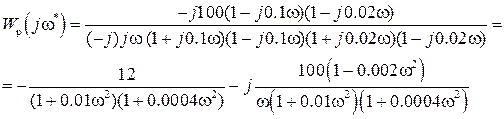
Определим величину 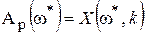
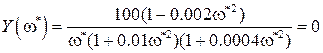
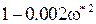
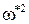
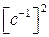
При подстановке этого значения частоты в X( 
отсюда следует, что замкнутая САР неустойчива.
kгр 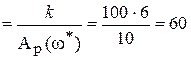
П. IV. 10. Предыдущий пример решить с помощью логарифмического критерия устойчивости.
В предыдущем примере мы нашли, что АФХ разомкнутой системы имеет вид
Получим отсюда выражение для АЧХ Ap( 
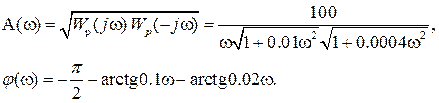
Имея в виду, что
а сопрягающие частоты
Построим асимптотическую ЛАЧХ и качественный вид ФЧХ разомкнутой системы.
Найдем частоту среза 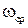
запишем выражение для ЛАЧХ на втором участке
На частоте среза 
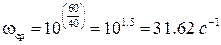
Значение фазочастотной характеристики 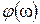
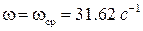
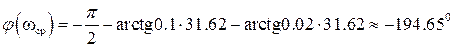
Следовательно, запас устойчивости по фазе для данной системы будет отрицательным
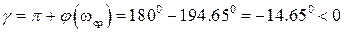
а сама система в замкнутом состоянии неустойчива.
Граничный коэффициент усиления 
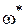
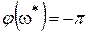
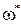

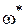
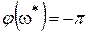
Из (IV. 3. 19) получим
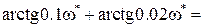
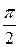
Из тригонометрии известно, что
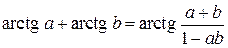
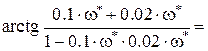
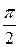
Величине 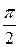
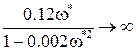
а это для 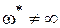
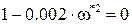
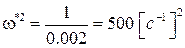
а сама частота 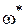
Величину 
Подставим сюда 
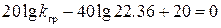
Отсюда 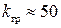
В предыдущем примере для той же задачи мы получили 

Вопросы для самопроверки.
1. Что понимается под устойчивостью системы?
2. Каковы признаки устойчивости САР?
3. Сформулируйте условие Стодолы.
4. Как найти граничное значение параметра по критерию устойчивости Гурвица.
5. Расскажите о принципе аргумента.
6. Что такое годограф Михайлова? Как он проходит в случае границы устойчивости системы?
7. Сформулируйте критерий устойчивости Найквиста для всех трех видов устойчивости разомкнутой САР.
8. Прокомментируйте связь логарифмического критерия устойчивости с критерием Найквиста.
9. Какие запасы устойчивости Вы знаете?
Дата добавления: 2016-04-14 ; просмотров: 4909 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
- Теория автоматического управления
- Реферат: Устойчивость дискретных систем управления
- Пример 1. Определить устойчивость дискретной системы с передаточной функцией
- Пример 2. Определить устойчивость дискретной системы с передаточной функцией
- Пример 3. Определить устойчивость дискретной системы с передаточной функцией
- Пример 4. Определить устойчивость дискретной системы, структурная схема которой представлена на рис. 2.
- .
- Пример 5. Определить устойчивость дискретной системы с передаточной функцией
- Пример 6. Определить устойчивость дискретной системы, структурная схема которой представлена на рис. 4.
- Передаточная функция замкнутой дискретной системы
- Передаточная функция замкнутой дискретной системы в форме z – преобразования
- Замкнутая дискретная система устойчива, если амплитудно-фазовая частотная характеристика разомкнутой устойчивой системы не охватывает току с координатами (–1,j0).
- 📹 Видео
Видео:proТАУ: 1. Передаточная функцияСкачать

Теория автоматического управления
Запишем передаточную функцию разомкнутой системы:
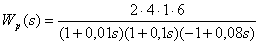
Передаточная функция замкнутой системы имеет вид:
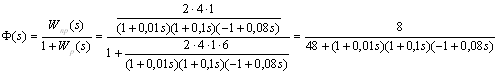
Характеристическое уравнение замкнутой системы:
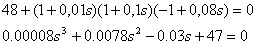
Корни характеристического уравнения (2):
Характеристическое уравнение (2) имеет два правых корня, следовательно, данная замкнутая система неустойчива.
1.2 Анализ устойчивости системы по алгебраическому критерию
Для характеристического уравнения (2) замкнутой системы коэффициенты ai, i=0..3,
Необходимым условием устойчивости системы является:
Данное условие не выполняется (a2
Видео:Характеристическое уравнение в ДУСкачать

Реферат: Устойчивость дискретных систем управления
| Название: Устойчивость дискретных систем управления Раздел: Рефераты по коммуникации и связи Тип: реферат Добавлен 04:40:43 28 августа 2009 Похожие работы Просмотров: 2036 Комментариев: 21 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
Дискретная система автоматического управления устойчива, если все корни ее характеристического уравнения расположены в левой полуплоскости в пределах основной полосы.
Видео:Устойчивость систем по критерию Гурвица ПримерыСкачать

Пример 1. Определить устойчивость дискретной системы с передаточной функцией

Решение: Характеристическое уравнение системы имеет вид
Определим корни характеристического уравнения

Система устойчива, так как все корни ее характеристического уравнения расположены в левой полуплоскости в пределах основной полосы.
Видео:РК9. Теория автоматического управления. Корректирующие устройства и методы их синтезаСкачать

Пример 2. Определить устойчивость дискретной системы с передаточной функцией
Характеристическое уравнение имеет вид

Определим корни характеристического уравнения заданной системы

Система на границе устойчивости, так как один корень расположен на мнимой оси, а второй устойчивый.
2. Определение устойчивости дискретных систем в форме z —преобразования
Использование z -преобразования позволяет преобразовать трансцендентный полином в степенной, что позволяет упростить процесс исследования дискретных систем управления.
Применение z -преобразования (рис. 2.3) отображает основную полосу на плоскость Z , отрезок мнимой оси 
Следовательно, дискретная система устойчива, если все корни ее характеристического уравнения расположены в левой полуплоскости в пределах основной полосы (т. е. условие устойчивости 
Видео:РК9. Теория автоматического управления. Критерий устойчивости НайквистаСкачать

Пример 3. Определить устойчивость дискретной системы с передаточной функцией

Характеристическое уравнение имеет вид

Определим корни характеристического уравнения
Определим модуль корней

Система не устойчива, так как модуль корней ее характеристического уравнения меньше единицы.
Видео:РК9. Теория автоматического управления. Алгебраические критерии устойчивости. Границы устойчивостиСкачать

Пример 4. Определить устойчивость дискретной системы, структурная схема которой представлена на рис. 2.
 |

Решение: Передаточная функция разомкнутой дискретной системы

Передаточная функция разомкнутой дискретной системы в форме z — преобразования


Передаточная функция замкнутой дискретной системы в форме z — преобразования
Видео:РК9. Теория автоматического управления. Понятие устойчивости линеаризованных системСкачать

 .
.
Характеристическое уравнение имеет вид 
Определим корни характеристического уравнения
При этом модуль корня 
3. Определение устойчивости дискретных систем в форме w — преобразования
Из теории функций комплексного переменного известно, что билинейное преобразование (w -преобразование, преобразование Мизеса) отображает круг единичного радиуса в плоскости Z во всю левую полуплоскость плоскости W , при использовании подстановки


Установим связь между плоскостями Z и W (см. рис. 3).
 |
 |
1. При½z ½ = 1 ,½w+1 ½ = ½w-1 ½, что соответствует оси j.
2. При½z ½ 1 ,½w+1 ½ > ½w-1 ½ — соответствует правой полуплоскости.
Дискретная система автоматического управления устойчива, если все корни ее характеристического уравнения расположены в левой полуплоскости плоскости W .
Следовательно, при использовании билинейного преобразования условия устойчивости непрерывных систем можно использовать для дискретных систем управления.
Видео:23) Построение Л.А.Ч.Х. и Л.Ф.Ч.Х. системы по её передаточной функцииСкачать

Пример 5. Определить устойчивость дискретной системы с передаточной функцией

Характеристическое уравнение имеет вид

Определим корни характеристического уравнения
Система устойчива, так как корни ее характеристического уравнения расположены в левой полуплоскости.
Видео:Частотные характеристики | Утро с теорией управления, лекция 5Скачать

Пример 6. Определить устойчивость дискретной системы, структурная схема которой представлена на рис. 4.
 |

Решение: Передаточная функция разомкнутой дискретной системы в форме z – преобразования


Видео:Артеменко М.В. Лекция №5 «Теория автоматического управления Устойчивость и качество»Скачать

Передаточная функция замкнутой дискретной системы

Характеристическое уравнение системы имеет вид

Выполнив билинейное преобразование, получим
Условие устойчивости: 1 – b > 0, 1 + b +d > 0, где b = [k(1-d)-(1+d)].
4. Применение критериев устойчивости для дискретных систем
Все критерии устойчивости, которые используются для анализа устойчивости непрерывных систем, могут быть использованы для дискретных систем с учетом некоторых особенностей.
Критерий устойчивости Гурвица можно использовать при применении билинейного преобразования. Рассмотри алгоритм его использования.
1. Записываем характеристическое уравнение D(z) = 0

2. Выполняем подстановку 

3. Составляем определитель Гурвица

4. Определяем устойчивость также как и для непрерывных систем.
Линейная дискретная система устойчива, если при 
Рассмотрим частные случаи.
При n = 1 характеристическое уравнение имеет вид
При n = 2 характеристическое уравнение имеет вид
Условие устойчивости: a0 > 0, a1 > 0, a2 > 0, а также:
Пример Определить устойчивость дискретной системы, если передаточная функция разомкнутой системы в форме z – преобразования, имеет вид

Видео:Видеометодичка. Практикум по нахождению передаточных функций по дифференциальным уравнениямСкачать

Передаточная функция замкнутой дискретной системы в форме z – преобразования

Характеристическое уравнение имеет вид

Выполним билинейное преобразование
Система не устойчива.
Критерий устойчивости Михайлова
Доказательство частотных критериев устойчивости базируется на следствии из принципа аргумента. Рассмотрим, как он формулируется для дискретных систем.
Пусть задано характеристическое уравнение замкнутой системы

Рассмотрим комплексную плоскость Z (рис. 7), пусть z2 расположен внутри круга единичного радиуса, а z1 вне него.

Если замкнутая система устойчива, то все корни расположены в пределах окружности единичного радиуса, а значит

Замкнутая дискретная система устойчива, если характеристическая кривая D*(jw) при изменении частоты 0 £w£p/T последовательно проходит 2n квадрантов.
Порядок построения характеристической кривой: определяем D(z) ; выполняем подстановку 

 |
Пример 8. Определить устойчивость по критерию Михайлова системы, схема которой приведена на рис. 6, если T = 1 с, kv = 2 c -1 .
 |
 |

Решение: Передаточная функция разомкнутой системы

Передаточная функция разомкнутой дискретной системы

Передаточная функция разомкнутой дискретной системы в форме z – преобразования
Передаточная функция замкнутой дискретной системы в форме z – преобразования

Характеристический полином имеет вид

Изменяя частоту в пределах 0 £w£p (0 £w£p/T) строим годограф Михайлова (рис. 7).
|
|
| w | 0 | p/4 | p/2 | p3/4 | p |
| X*(w) | 2 | 1+Ö2/2 | 1 | 1-Ö2/2 | 0 |
| Y*(w) | 0 | Ö2/2 | 1 | Ö2/2 | 0 |
Как видно из рисунка система находится на границе устойчивости.
Проверим по критерию Гурвица при
Корень находится на окружности единичного радиуса, следовательно, система находится на границе устойчивости.
Критерий устойчивости Михайлова с использованием билинейного преобразования
При этом исходным является характеристический полином в форме z -преобразования. Выполним подстановку

При этом критерий Михайлова для дискретных систем применяется в таком же виде, как и для непрерывных систем.
Пример 9. Определить условие устойчивости по критерию Михайлова дискретной системы, схема которой приведена на рис. 6.
Характеристический полином имеет вид

Выполнив подстановку z = (1+w)/(1-w) , в характеристический полином получим

Выполнив подстановку w = j l , в характеристический полином получим
Строим график рис. 8. Система устойчива при kv T > 2. Критический коэффициент усиления равен kv кр = 2/T.
Критерий устойчивости Найквиста
Рассмотрим функцию, которая связывает характеристики разомкнутых и замкнутых дискретных систем

где D*(p) – характеристический полином замкнутой системы;
A*(p) – характеристический полином разомкнутой системы.
В соответствии со следствием из принципа аргумента

Рассмотрим разные случаи.
Система, устойчивая в разомкнутом состоянии
Так как разомкнутая дискретная система устойчива, то она не содержит корней в правой полуплоскости (т. е. m = 0), для того чтобы и замкнутая дискретная система была устойчива, должно выполняться условие

Формулировка критерия Найквиста:
Видео:ЛСАР Лекция №10 Критерий МихайловаСкачать

Замкнутая дискретная система устойчива, если амплитудно-фазовая частотная характеристика разомкнутой устойчивой системы не охватывает току с координатами (–1,j0).
Графически это обозначает, что годограф вектора W*(j w ) не охватывает начала координат, а вектора K*(j w ) -точку с координатами (-1, j0 ).
Система, неустойчивая в разомкнутом состоянии
Так как разомкнутая система неустойчива, то она содержит m корней в правой полуплоскости, для того чтобы замкнутая система была устойчива, должно выполняться условие:
Графически это обозначает, что годограф вектора K(j w ) охватывает точку с координатами (-1, j0 ) m –раз.
Формулировка критерия Найквиста: Замкнутая дискретная система устойчива, если амплитудно-фазовая частотная характеристика разомкнутой неустойчивой системы, имеющей m корней в правой полуплоскости, охватывает току с координатами (–1 , j0) m раз.
Пример 10. Определить условия устойчивости и величину критического коэффициента усиления по критерию Найквиста дискретной системы, схема которой приведена на рис. 6.
Решение: Передаточная функция разомкнутой дискретной системы в форме z – преобразования
При этом выражение для частотной характеристики имеет вид
Строим частотную характеристику дискретной системы в соответствии с таблицами 2 и 3 (рис. 9).
Характеристику строим на интервале частот 0 £ w £ p /T в дальнейшем характеристики повторяются, так как они носят периодический характер.
Условие устойчивости данной дискретной системы определяется соотношением kv T/2 = 1 . 0 £w£p/T
| w | 0 | p/2T | p/T |
| P*(w) | -kv T/2 | -kv T/2 | -kv T/2 |
| Q*(w) | -¥ | -kv T/2 | 0 |
 |
| a | 0 | 30 | 45 | 60 | 90 |
| ctga | -¥ | Ö3 | 1 | 1/Ö3 | 0 |
Критический коэффициент усиления системы равен kv кр = 2/Т .
1. Дорф Р., Бишоп Р. Автоматика. Современные системы управления. 2002г. – 832с.
2. Харазов В. Г. Интегрированные системы управления технологическими процессами: Справочник. Издательство: ПРОФЕССИЯ, ИЗДАТЕЛЬСТВО, 2009. – 550с.
3. Чебурахин И. Синтез дискретных управляющих систем и математическое моделирование: теория, алгоритмы, программы. Изд-во: НИЦ РХД, ФИЗМАТЛИТ®, 2004. – 248c.
📹 Видео
Теория автоматического управления. Лекция 9. Критерий ГурвицаСкачать

Теория автоматического управления. Лекция 22. D-разбиение по двум параметрамСкачать

Артеменко М.В. Лекция №5 «Оценка устойчивости и качества САУ»Скачать

29) КРИТЕРИИ УСТОЙЧИВОСТИ. КРИТЕРИЙ ГУРВИЦАСкачать

Лемак С. С. - Механика управляемых систем - Лекция 8Скачать

Теория автоматического управления. Лекция 10. Критерий МихайловаСкачать

Регуляторы и астатизмы | Утро с теорией управления, лекция 4Скачать

2020.04.21 В.А. Александров «Оптимизация размещения полюсов в одномерной системе управления»Скачать

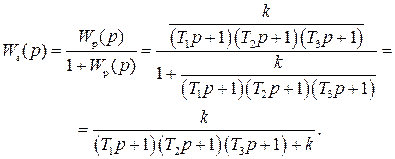
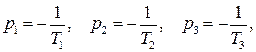
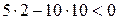
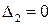
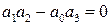
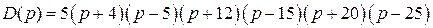
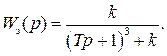
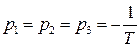
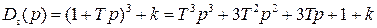
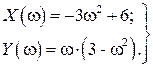
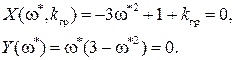
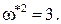
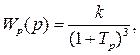
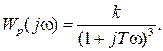
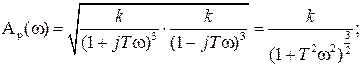
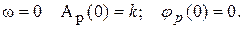
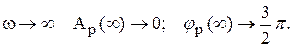
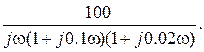
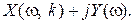
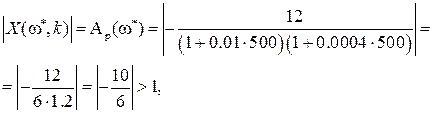
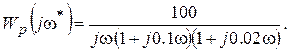
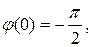
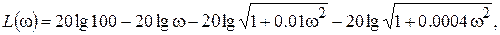
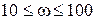
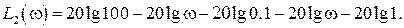
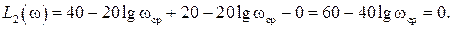

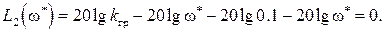
 . (1)
. (1) представляет собой степенное уравнение, при этом число корней уравнения равно степени полинома — n .
представляет собой степенное уравнение, при этом число корней уравнения равно степени полинома — n .

 .(2)
.(2) представляет собой трансцендентное уравнение, при этом число корней уравнения бесконечно, так как они имеют периодический характер.
представляет собой трансцендентное уравнение, при этом число корней уравнения бесконечно, так как они имеют периодический характер. (3)
(3) .
. .
.



 .
.












