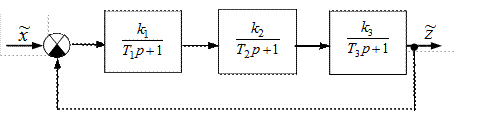
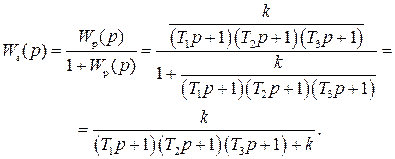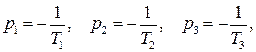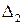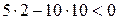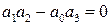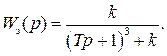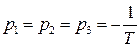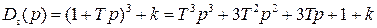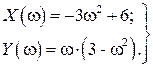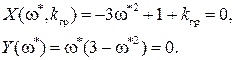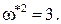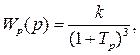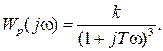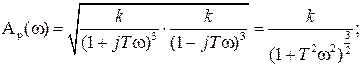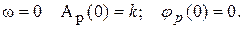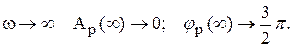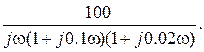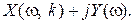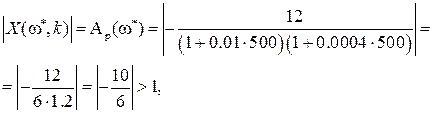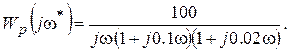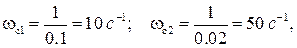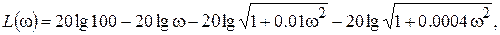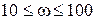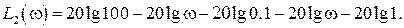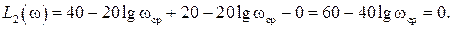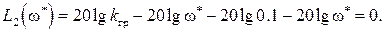В замкнутой САР (рис. IV. 27) заданы (в числовом выражении)
Рис. IV. 27. Функциональная схема замкнутой САР
Определить устойчивость разомкнутой и замкнутой САР и найти kгр.
Для решения поставленной задачи воспользуемся критерием Гурвица. Найдем передаточные функции, а затем и характеристические уравнения разомкнутой и замкнутой систем.
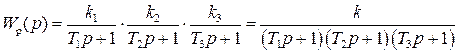
где 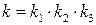
Для разомкнутой системы характеристическое уравнение имеет вид
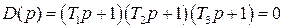
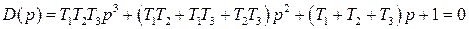
а для замкнутой САР получается
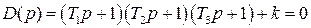
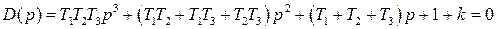
Нетрудно понять, что для исследования устойчивости разомкнутой САР применять критерий устойчивости Гурвица излишне, ибо непосредственно из вида характеристического уравнения разомкнутой системы (IV. 3. 11) легко найти, что все корни левые
т. е. разомкнутая САР при всегда положительных Т1, Т2, Т3 устойчива.
Вот по виду характеристического уравнения замкнутой САР (IV. 3. 12) так просто, как в предыдущем случае, определить соответствующие корни не удается, поэтому приходится применить критерий устойчивости Гурвица . При введении обозначений
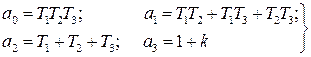
характеристическое уравнение замкнутой САР (IV. 3. 13) примет вид
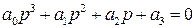
В разделе IV. 2. 2 было выяснено, что для САР с характеристическим уравнением третьего порядка для устойчивости необходимо и достаточно при положительных коэффициентах ai( i =0, 1, 2,3) выполнение условия ( IV. 2. 3)
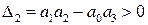
Из (IV. 3. 14) видно, условия ai>0 при положительных Т1, Т2, Т3 и k всегда выполняются, а для проверки условия (IV. 2.3) надо в него подставить заданные значения параметров Т1, Т2, Т3 и k и определить знак минора
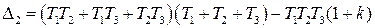
Если этот минор больше нуля, то заданная замкнутая САР устойчива.
Граничный коэффициент усиления kгр найдется из предпоследнего минора, приравненного к нулю
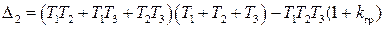
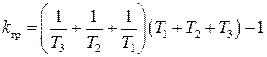
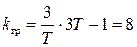
Характеристическое уравнение САР имеет вид
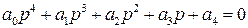
Определить устойчивость САР.
Так как заданное характеристическое уравнение 4-го порядка имеет один неположительный коэффициент (а4=0), то, согласно условию Стодолы (что в данном случае совпадает с критерием Гурвица) САР не сожжет быть устойчивой, а только либо нейтральной либо неустойчивой.
Запишем заданное характеристическое уравнение в другом виде
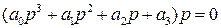
Видно, что один из корней – нулевой. САР будет находиться на границе устойчивости, если все остальные корни характеристического уравнения левые (при наличии хотя бы одного правого корня САР будет неустойчивой). Эти остальные корни будут левыми, если выполняются условия устойчивости для уравнения
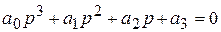
а именно (согласно разделу IV. 2. 2)
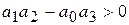
После подстановки значений коэффициентов последнее неравенство
не выполняется, следовательно САР неустойчива.
Передаточная функция разомкнутой САР имеет вид
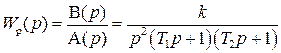
Определить устойчивость замкнутой САР.
Характеристическое уравнение замкнутой САР определяется выражением
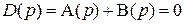
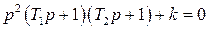
После простого преобразования получим
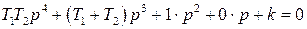
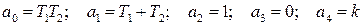
Согласно критерию Гурвица для устойчивости системы необходимо, чтобы все ai( i=0, 1, 2, 3, 4) > 0. В нашем же случае 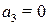
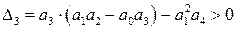
Учитывая что 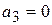
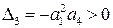
Поскольку 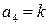
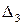
Переходная функция разомкнутой САР имеет вид
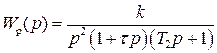
где 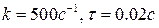
Определить постоянную времени Тгр, при которой замкнутая САР находиться на границе устойчивости.
Получим характеристическое уравнение замкнутой САР
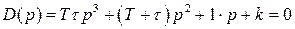
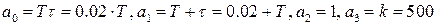
Граница устойчивости определяется из равенства нулю второго минора
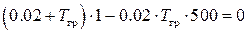
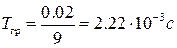
Характеристический полином САР 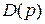
Каково изменение аргумента 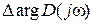
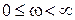
Характеристическое уравнение 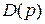
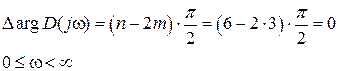
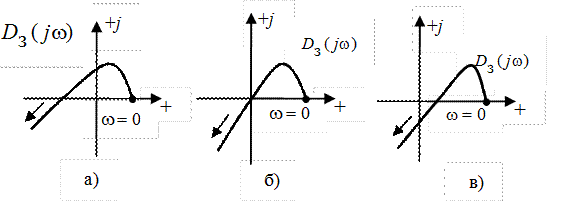
Какой из указанных годографов Михайлова замкнутой системы
Рис. IV. 28. Годографы Михайлова для устойчивой, нейтральной и неустойчивой замкнутой систем.
соответствует САР с передаточной функцией
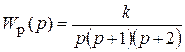
Характеристический полином замкнутой системы имеет вид
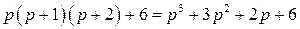
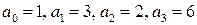
Для этого полинома второй минор оказывается равный нулю
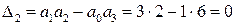
т.е. замкнутая САР находится на границе устойчивости, что соответствует годографу Михайлова, имеющему вид рис. IV. 28, б.
Определить устойчивость разомкнутой и замкнутой САР и найти kгр.
Запишем передаточные функции разомкнутой
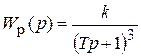
а замкнутой САР
Поскольку из характеристического уравнения разомкнутой САР
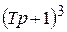
следует, что все три его корня
при положительном Т есть левые, то, значит, разомкнутая САР устойчива.
Для определения устойчивости замкнутой САР применим критерий Михайлова.
Характеристический полином замкнутой системы, имеющий третий порядок,
после замены 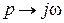
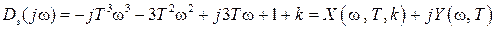
В этом выражении мы выделили действительную часть 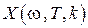
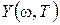
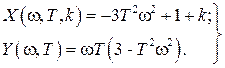
Ответ на вопрос – устойчива ли замкнутая САР можно получить по виду годографа Михайлова, зависящего от конкретных значений параметров k и T. Пусть для определенности k =5, T =1 с. Тогда соотношения (IV. 3. 15) примут
Задаваясь численными значениями 
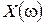
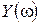

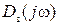
 | 1.42 | 1.5 | 1.73 | ∞ |
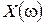 | -0.75 | -3 | -6 | ∞ |
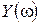 | 1.42 | 1.125 | -2 | ∞ |
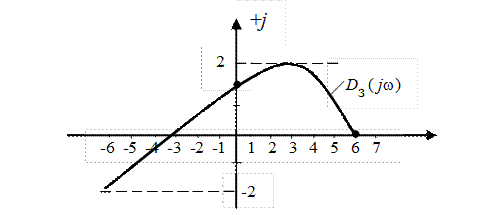
Рис. IV. 29. Годограф Михайлова.
Поскольку годограф Михайлова, начинается на положительном отрезке действительной оси, с ростом частоты от 0 до 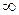
Определим теперь kгр. В разделе IV. 3. 2 было показано, что на границе устойчивости годограф Михайлова проходит через начало координат, т.е. выполняются условия (IV. 3. 4) .
В нашем случае при k = kгр, 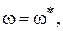
Из второго из этих уравнений, отбрасывая неверное решение 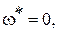
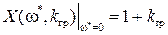
Подставляя это значение граничной частоты в выражение для 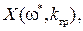
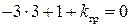
т.е. kгр = 8, как и в примере П. IV. 1.
П. IV. 8. Предыдущую задачу П. IV. 7. решить с помощью критерия Найквиста.
Передаточную функцию разомкнутой системы мы получили в виде
откуда ясно, что все корни характеристического уравнения левые и, значит, разомкнутая система устойчива.
Если провести замену 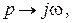
Построим эту характеристику. Найдем сначала 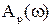
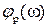
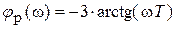
При
При
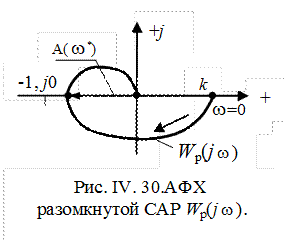
Следовательно, качественно АФХ разомкнутой системы Wp(j 
Устойчивость системы в замкнутом состоянии зависит от того, охватывает ли 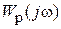




Из заданной операторной формы управления системы получим
Wp(j 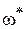
В отличии от предыдущего примера для разнообразия АФХ разомкнутой САР Ap( 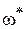
Wp(j 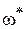
Для этого нужно освободиться от мнимости в знаменателе выражения для
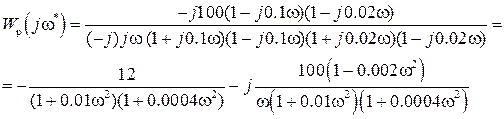
Определим величину 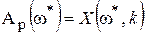
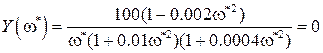
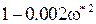
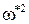
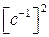
При подстановке этого значения частоты в X( 
отсюда следует, что замкнутая САР неустойчива.
kгр 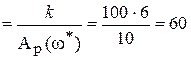
П. IV. 10. Предыдущий пример решить с помощью логарифмического критерия устойчивости.
В предыдущем примере мы нашли, что АФХ разомкнутой системы имеет вид
Получим отсюда выражение для АЧХ Ap( 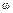
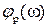
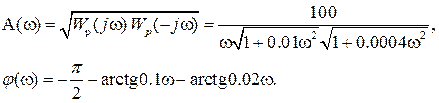
Имея в виду, что
а сопрягающие частоты
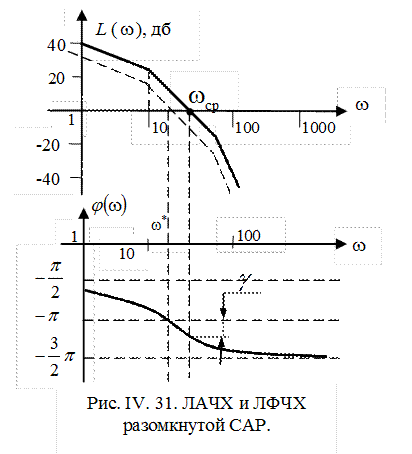
Построим асимптотическую ЛАЧХ и качественный вид ФЧХ разомкнутой системы.
Найдем частоту среза 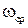
запишем выражение для ЛАЧХ на втором участке
На частоте среза 
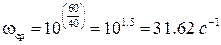
Значение фазочастотной характеристики 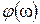
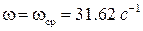
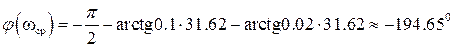
Следовательно, запас устойчивости по фазе для данной системы будет отрицательным
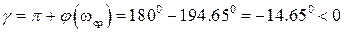
а сама система в замкнутом состоянии неустойчива.
Граничный коэффициент усиления 
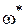
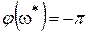

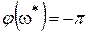
Из (IV. 3. 19) получим
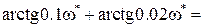
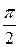
Из тригонометрии известно, что
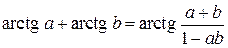
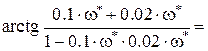
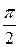
Величине 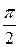
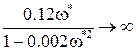
а это для 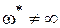
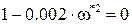
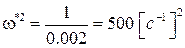
а сама частота 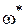
Величину 
Подставим сюда 
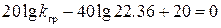
Отсюда 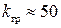
В предыдущем примере для той же задачи мы получили 

Вопросы для самопроверки.
1. Что понимается под устойчивостью системы?
2. Каковы признаки устойчивости САР?
3. Сформулируйте условие Стодолы.
4. Как найти граничное значение параметра по критерию устойчивости Гурвица.
5. Расскажите о принципе аргумента.
6. Что такое годограф Михайлова? Как он проходит в случае границы устойчивости системы?
7. Сформулируйте критерий устойчивости Найквиста для всех трех видов устойчивости разомкнутой САР.
8. Прокомментируйте связь логарифмического критерия устойчивости с критерием Найквиста.
9. Какие запасы устойчивости Вы знаете?
Дата добавления: 2016-04-14 ; просмотров: 4908 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:10. Линейные однородные рекуррентные соотношения. Дискретная математикаСкачать

Критерии устойчивости (Лекция)
2. Корневой критерий
3. Критерий Стодолы
4. Критерий Гурвица
5. Критерий Михайлова
6. Критерий Найквиста
7. Показатели качества
8. Прямые показатели качества
9. Корневые показатели качества
10. Частотные показатели качества
Важным показателем АСР является устойчивость, поскольку основное ее назначение заключается в поддержании заданного постоянного значения регулируемого параметра или изменение его по определенному закону. При отклонении регулируемого параметра от заданной величины (например, под действием возмущения или изменения задания) регулятор воздействует на систему таким образом, чтобы ликвидировать это отклонение. Если система в результате этого воздействия возвращается в исходное состояние или переходит в другое равновесное состояние, то такая система называется устойчивой. Если же возникают колебания со все возрастающей амплитудой или происходит монотонное увеличение ошибки е, то система называется неустойчивой.
Для того, чтобы определить, устойчива система или нет, используются критерии устойчивости:
1) корневой критерий,
2) критерий Стодолы,
3) критерий Гурвица,
4) критерий Найквиста,
5) критерий Михайлова и др.
Первые два критерия являются необходимыми критериями устойчивости отдельных звеньев и разомкнутых систем. Критерий Гурвица является алгебраическим и разработан для определения устойчивости замкнутых систем без запаздывания. Последние два критерия относятся к группе частотных критериев, поскольку определяют устойчивость замкнутых систем по их частотным характеристикам. Их особенностью является возможность применения к замкнутым системам с запаздыванием, которыми является подавляющее большинство систем управления.
2. Корневой критерий
Корневой критерий определяет устойчивость системы по виду передаточной функции. Динамической характеристикой системы, описывающей основные поведенческие свойства, является характеристический полином, находящийся в знаменателе передаточной функции. Путем приравнивания знаменателя к нулю можно получить характеристическое уравнение, по корням которого определить устойчивость.
Корни характеристического уравнения (они обозначены звездочкой) могут быть как действительные, так и комплексные и для определения устойчивости откладываются на комплексной плоскости.
Виды корней характеристического уравнения:
положительные (корень № 1);
комплексные сопряженные (4);
По кратности корни бывают:
одиночные (1, 2, 3);
сопряженные (4, 5): si = a ± j w ;
Корневой критерий формулируется следующим образом:
Линейная АСР устойчива, если все корни характеристического уравнения лежат в левой полуплоскости. Если хотя бы один корень находится на мнимой оси, которая является границей устойчивости, то говорят, что система находится на границе устойчивости. Если хотя бы один корень находится в правой полуплоскости (не зависимо от числа корней в левой), то система является неустойчивой.
Иными словами, все действительные корни и действительные части комплексных корней должны быть отрицательны. В противном случае система неустойчива.
Пример 4.1. Передаточная функция системы имеет вид:

Характеристическое уравнение: s 3 + 2 s 2 + 2.25 s + 1.25 = 0.
Следовательно, система устойчива.
3. Критерий Стодолы
Этот критерий является следствием из предыдущего и формулируется следующим образом: Линейная система устойчива, если все коэффициенты характеристического полинома положительны.
То есть, для передаточная из примера 4.1 по критерию Стодола соответствует устойчивой системе.
4. Критерий Гурвица
Критерий Гурвица работает с характеристическим полиномом замкнутой системы. Как известно, структурная схема АСР по ошибке имеет вид, как показано на рисунке ниже.
Wp — передаточная функция регулятора,
Wy — передаточная функция объекта управления.
Определим передаточную функцию для прямой связи (передаточную функцию разомкнутой системы): W ¥ = Wp Wy .
Далее с учетом наличия отрицательной обратной связи получаем передаточную функцию замкнутой системы:

Как правило, передаточная функция разомкнутой системы имеет дробно-рациональный вид:

Тогда после подстановки и преобразования получаем:

Отсюда следует, что характеристический полином замкнутой системы (ХПЗС) можно определить как сумму числителя и знаменателя W ¥ :
D з( s ) = A ( s ) + B ( s ).
Для определения устойчивости по Гурвицу строится матрица таким образом, чтобы по главной диагонали были расположены коэффициенты ХПЗС с an +1 по a 0. Справа и слева от нее записываются коэффициенты с индексами через 2 ( a 0, a 2, a 4… или a 1, a 3, a 5 …). Тогда для устойчивой системы необходимо и достаточно, чтобы определитель и все главные диагональные миноры матрицы были больше нуля.
Если хотя бы один определитель будет равен нулю, то система будет находится на границе устойчивости.
Если хотя бы один определитель будет отрицателен, то система неустойчива не зависимо от числа положительных или нулевых определителей.
Пример. Дана передаточная функция разомкнутой системы

Требуется определить устойчивость замкнутой системы по критерию Гурвица .
Для этого определяется ХПЗС :
D(s) = A(s) + B(s) = 2s 4 + 3s 3 + s 2 + 2s 3 + 9s 2 + 6s + 1 = 2s 4 + 5s 3 + 10s 2 + 6s + 1.
Поскольку степень ХПЗС равна n = 4, то матрица будет иметь размер 4х4. Коэффициенты ХПЗС равны а4 = 2, а3 = 5, а2 = 10, а1 = 6, а0 = 1.
Матрица имеет вид:
(обратите внимание на сходство строк матрицы: 1 с 3 и 2 с 4). Определители:

Поскольку все определители положительны, то АСР устойчива.
5. Критерий Михайлова
Описанные выше критерии устойчивости не работают, если передаточная функция системы имеет запаздывание, то есть может быть записана в виде

где t — запаздывание.
В этом случае характеристическое выражение замкнутой системы полиномом не является и его корни определить невозможно. Для определения устойчивости в данном случае используются частотные критерии Михайлова и Найквиста.
Порядок применения критерия Михайлова:
1) Записывается характеристическое выражение замкнутой системы:
D з (s) = A(s) + B(s) . e — t s .
2) Подставляется s = j w : D з (j w ) =Re( w ) + Im( w ).
3) Записывается уравнение годографа Михайлова D з( j w ) и строится кривая на комплексной плоскости.
Для устойчивой АСР необходимо и достаточно, чтобы годограф Михайлова (см. рис.), начинаясь при w = 0 на положительной вещественной полуоси, обходил последовательно в положительном направлении (против часовой стрелки) при возрастании w от 0 до ¥ n квадрантов, где n — степень характеристического полинома.
Если годограф Михайлова проходит через начало координат, то говорят, что система находится на границе устойчивости.
6. Критерий Найквиста
Данный критерий аналогичен критерию Михайлова, но работает с АФХ системы, поэтому более сложен для расчетов.
1) Определяется передаточная функция разомкнутой системы 
2) Определяется число правых корней m .
3) Подставляется s = j w : W ¥ ( j w ).
4) Строится АФХ разомкнутой системы.
Для устойчивости АСР необходимо и достаточно, чтобы при увеличении w от 0 до ¥ АФХ W ¥ ( j w ) m раз охватывала точку (-1; 0), где m — число правых корней разомкнутой системы.
Если АФХ проходит через точку (-1; 0), то замкнутая система находится на границе устойчивости.
В случае, если характеристическое уравнение разомкнутой системы A ( s ) = 0 корней не имеет (т.е. m = 0), то критерий, согласно критерию, замкнутая система является устойчивой, если АФХ разомкнутой системы W ¥ ( j w ) не охватывала точку (-1; 0), в противном случае система будет неустойчива (или на границе устойчивости).
7. Показатели качества
Если исследуемая АСР устойчива, то может возникнуть вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям. На практике качество регулирования может быть определено визуально по графику переходной кривой, однако, имеются точные методы, дающие конкретные числовые значения.
Показатели качества разбиты на 4 группы:
1) прямые — определяемые непосредственно по кривой переходного процесса,
2) корневые — определяемые по корням характеристического полинома,
3) частотные — по частотным характеристикам,
4) интегральные — получаемые путем интегрирования функций.
8. Прямые показатели качества
К ним относятся: степень затухания y , перерегулирование s , статическая ошибка ест, время регулирования tp и др.

Предположим, переходная кривая, снятая на объекте, имеет колебательный вид (см. рис. 1.38).
Сразу по ней определяется установившееся значение выходной величины ууст.
Степень затухания y определяется по формуле

где А1 и А3 — соответственно 1-я и 3-я амплитуды переходной кривой.
Перерегулирование s = 
Статическая ошибка ест = х — ууст, где х — входная величина.
Время достижения первого максимума t м определяется по графику.
Время регулирования tp определяется следующим образом: Находится допустимое отклонение D = 5% ууст и строится «трубка» толщиной 2 D . Время tp соответствует последней точке пересечения y ( t ) с данной границей. То есть время, когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.
9. Корневые показатели качества
К ним относятся: степень колебательности m , степень устойчивости h и др.
Не требуют построения переходных кривых, поскольку определяются по корням характеристического полинома. Для этого корни полинома откладываются на комплексной плоскости и по ним определяются:
Степень устойчивости h определяется как граница, правее которой корней нет, т.е.
h = min 
где Re ( si ) — действительная часть корня si .
Степень колебательности m рассчитывается через угол g : m = tg g . Для определения g проводятся два луча, которые ограничивают все корни на комплексной плоскости. g — угол между этими лучами и мнимой осью. Степень колебательности может быть определена также по формуле:
m = min 
10. Частотные показатели качества
Для определения частотных показателей качества требуется построение АФХ разомкнутой системы и АЧХ замкнутой системы.
По АФХ определяются запасы: D A — по амплитуде, D j — по фазе.
Запас D A определяется по точке пересечения АФХ с отрицательной действительной полуосью.
Для определения D j строится окружность единичного радиуса с центром в начале координат. Запас D j определяется по точке пересечения с этой окружностью.
По АЧХ замкнутой системы определяются показатели колебательности по заданию М и ошибке МЕ как максимумы соответственно АЧХ по заданию и АЧХ по ошибке.
Связи между показателями качества.Описанные выше показатели качества связаны между собой определенными соотношениями:




Видео:21.04 - дискра, рекуррентные соотношенияСкачать
Типовые передаточные функции и характеристическое уравнение
Для описания системы вводят передаточные функции, связывающие определенные входы и выходы.
1. Передаточная функция разомкнутой системы определяется как произведение всех передаточных функций по основному контуру. Она единственная и не зависит от точки размыкания:
2. Передаточная функция замкнутой системы по задающему воздействию определяется как отношение изображения выходной координаты (в данном случае – скорости вращения двигателя) к изображению задающего воздействия:
3. Передаточная функция замкнутой системы по возмущающему воздействию определяется как отношение изображения выходной координаты к изображению возмущающего воздействия (в данном случае – момента нагрузки):
Стандартная схема системы
В целях унификации вводится стандартная структурная схема системы с единичной обратной связью, стандартными обозначениями входов и выходов и типовых передаточных функций.
| Y(s) |
| F(s) |
| f |
| v |
| V(s) |
| y |
| W(s) |
| ε |
| E(s) |
Рисунок 7.2. стандартная схема системы
1. Передаточная функция разомкнутой системы:



2. Передаточная функция по задающему воздействию:
Приравниваем знаменатель к нулю, получаем характеристическое уравнение замкнутой системы.

3. Передаточная функция по возмущению:
4. Передаточная функция по ошибке:
Понятие устойчивости
Очень важно изучить поведение системы во времени. В некоторых случаях процессы оказываются расходящимися, что свидетельствует о неустойчивости системы.
Для нормальной эксплуатации система должна быть устойчивой, т.е. после действия возмущения она должна возвращаться в состояние равновесия.
В качестве примера рассмотрим поведение шарика на вогнутой поверхности (желоб), выпуклой поверхности и плоской поверхности.
Устойчивая система (вогнутая поверхность), процесс сходится:
| X |
| x0 |
| t |
Неустойчивая система (выпуклая поверхность), процесс расходится:
| t |
| X |
| x0 |
Нейтральная система (горизонтальная поверхность), координата (процесс) остается постоянной.
| t |
| x0 |
| X |
Эти примеры являются механической аналогией понятия устойчивости. Рассмотрим математическое определение понятия устойчивости.
| u(t) |
| Д.У. |
| y(t) |
| U(s) |
| W(s) |
| Y(s) |
Система описывается дифференциальным уравнением:






Строго устойчивость определяется в смысле Ляпунова. Для линейных систем с постоянными параметрами считается, что система устойчива, если предел свободной составляющей равен 0

Устойчивость — внутреннее свойство системы, присущее ей вне зависимости от действующих на нее сигналов, поэтому рассматривается только свободная составляющая.
Это есть определение асимптотической устойчивости.
Свяжем требование устойчивости с расположением корней характеристического уравнения:


вещественные обозначим 
комплексные – 
Рассмотрим свободные составляющие соответствующие различным корням.
1. Корень вещественный, положительный:
| +j |
| yсв |
 |
| + |
| пл.s |
| t |
| система неустойчива |
2. Корень вещественный, отрицательный:
 +j +j |
| +j |
| пл. s |
| + |
| yсв |
| t |
| система устойчива |
3. Корни комплексные, сопряженные, с положительной вещественной частью:
| +j |
 |
 |
| yсв |
 |
| + |
| пл. s |
| t |

4. Корни комплексные, сопряженные, с отрицательной вещественной частью:
| yсв |
| +j |
 |
 |
 |
| пл. s |
| + |
| t |

Условием устойчивости является расположение корней характеристического уравнения в левой полуплоскости.
Система на границе устойчивости, если корни на мнимой оси.
Устойчивость – необходимое условие функционирования системы, поэтому в курсе уделяется много внимания методам оценки устойчивости системы.
🔥 Видео
Характеристическое уравнение в ДУСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать

Лекция 1 | Теория автоматического управленияСкачать

Видеоурок "Системы дифференциальных уравнений"Скачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Теория автоматического управления. Лекция 9. Критерий ГурвицаСкачать

Теория автоматического управления. Лекция 23. Корневой метод Соколова Т.Н.Скачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать

Частотные характеристики | Утро с теорией управления, лекция 5Скачать

Модели, представленный системой двух дифференциальных уравненийСкачать

[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать
![[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]](https://i.ytimg.com/vi/agDRxLaUWI4/0.jpg)
Регуляторы и астатизмы | Утро с теорией управления, лекция 4Скачать

Модальные регуляторы и наблюдатели | Утро с теорией управления, лекция 8Скачать

23) Построение Л.А.Ч.Х. и Л.Ф.Ч.Х. системы по её передаточной функцииСкачать

29) КРИТЕРИИ УСТОЙЧИВОСТИ. КРИТЕРИЙ ГУРВИЦАСкачать