- Термин: Постоянная времени RC-цепи
- Дифференциальное уравнение [ править ]
- Обсуждение [ править ]
- Конкретные случаи [ править ]
- Определение постоянной времени. Переходные процессы в R-L-C-цепи.
- RC-цепи, 5 самых ходовых схем фильтров и их простой рассчет
- Постоянная времени RC — RC time constant
- Постоянная времени электрической цепи — что это такое и где используется
- Портал ТОЭ
- 6.2 Классический метод расчёта переходных процессов
- Составление характеристического уравнения
- Корни характеристического уравнения. Постоянная времени
- 🔥 Видео
Видео:Характеристическое уравнение в ДУСкачать

Термин: Постоянная времени RC-цепи
τ – постоянная времени RC-цепи – это временна́я характеристика простой электрической цепи, в которой происходит изменение заряда конденсатора С за счёт его разряда через сопротивление R. Постоянная времени вычисляется как τ=R*C [Ф*Ом], что эквивалентно размерности «секунда» [c].
Как показано на рисунке, постоянная времени τ входит в аналитическую функцию описания процесса изменения напряжения на конденсаторе U(t) при его заряде от источника напряжения через сопротивление R. На рисунке U(0) – это начальное напряжение на конденсаторе (в момент времени t=0), а U(∞) – это напряжение источника напряжения, к которому асимтотически стремится U(t).
За время, равное τ, напряжение на конденсаторе изменяется от U(0) до U(∞) + [U(0) — U(∞)]/e, где e=2,718. .
Экспоненциальный заряд конденсатора происходит для случая U(∞) > U(0), а экспоненциальный разряд – для случая U(∞) -t/τ ) в моменты времени t от t=0,001τ до t=10τ протекания экспоненциального процесса.
| Время процесса в единицах τ=RC | Доля неустановившейся величины напряжения e -t/τ | |
| *100, % | *10 6 , ppm | |
| 0,001τ | ≈99,9% | ≈999000 |
| 0,01τ | ≈99% | ≈990000 |
| 0,1τ | ≈90% | ≈900000 |
| 0,5τ | ≈61% | ≈610000 |
| τ | ≈37% | ≈370000 |
| 2τ | ≈14% | ≈140000 |
| 3τ | ≈5,0% | ≈50000 |
| 4τ | ≈1,8% | ≈1800 |
| 5τ | ≈0,67% | ≈6700 |
| 6τ | ≈0,25% | ≈2500 |
| 7τ | ≈0,091% | ≈910 |
| 8τ | ≈0,034% | ≈340 |
| 9τ | ≈0,012% | ≈120 |
| 10τ | ≈0,0045% | ≈45 |
Понятие постоянной времени RC-цепи помогает оценить время протекания процесса при анализе эквивалентных электрических схем, содержащих RC-цепи. Заметим только, что понятие постоянной времени не применимо для частного случая заряда-разряда конденсатора постоянным током, где закон изменения напряжения и заряда на конденсаторе имеет линейный характер, а не экспоненциальный.
Постоянные времени RC-цепей (в качестве величин с прозрачным физическим смыслом) участвуют в аналитических решениях дифференциальных уравнений, описывающих не только экспоненциальные процессы в электрических схемах, содержащих RC-цепи (например, пассивные и активные RC-фильтры).










Видео:Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Дифференциальное уравнение [ править ]
Основная статья: теория систем LTI
Системы LTI первого порядка характеризуются дифференциальным уравнением
τ d V d т + V знак равно ж ( т ) < Displaystyle тау < гидроразрыва
где τ представляет собой экспоненциальную константу затухания, а V является функцией времени t
V знак равно V ( т ) .
Правая часть — это вынуждающая функция
f
(
t
), описывающая внешнюю движущую функцию времени, которую можно рассматривать как
вход
системы , на который
V
(
t
) является
ответом
или выходом системы. Классические примеры для
f
(
t
) :
Функция Хевисайда , часто обозначается U
это начальное значение V . Таким образом, отклик представляет собой экспоненциальный спад с постоянной времени τ .
Обсуждение [ править ]
Такое поведение называется «убывающей» экспоненциальной функцией. Время τ (тау) называется «постоянной времени» и может использоваться (как в этом случае), чтобы указать, насколько быстро экспоненциальная функция затухает.
t = время (обычно
t
> 0 в технике управления)
V
0 = начальное значение (см. «Особые случаи» ниже).
Конкретные случаи [ править ]
1) Пусть ; тогда и так t = 0 V = V 0 e 0 <displaystyle V=V_e^> V = V 0 <displaystyle V=V_> 2) Пусть ; тогда t = τ V = V 0 e − 1 ≈ 0.37 V 0 <displaystyle V=V_e^approx 0.37V_> 3) Пусть , и так V = f ( t ) = V 0 e − t / τ <displaystyle V=f(t)=V_e^> lim t → ∞ f ( t ) = 0 <displaystyle lim _f(t)=0> 4) Пусть ; тогда t = 5 τ V = V 0 e − 5 ≈ 0.0067 V 0 <displaystyle V=V_e^approx 0.0067V_>
После периода в одну постоянную времени функция достигает e
−1 = примерно 37% от своего начального значения. В случае 4 после пяти постоянных времени функция достигает значения менее 1% от исходного. В большинстве случаев этот порог в 1% считается достаточным, чтобы предположить, что функция упала до нуля — как показывает опыт, в технике управления стабильной системой является система, которая демонстрирует такое общее затухающее поведение.
Видео:Лекция 091-5. Расчет переходных процессов классическим методом. Корни характеристического уравненияСкачать

Определение постоянной времени. Переходные процессы в R-L-C-цепи.
Переходные процессы в цепи с одним накопителем энергии и произвольным числом резисторов
Как отмечалось в предыдущей лекции, линейная цепь охвачена единым переходным процессом. Поэтому в рассматриваемых цепях с одним накопителем энергии (катушкой индуктивности или конденсатором) – цепях первого порядка – постоянная времени будет одной и той же для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение.
Общий подход к расчету переходных процессов в таких цепях основан на применении теоремы об активном двухполюснике: ветвь, содержащую накопитель, выделяют из цепи, а оставшуюся часть схемы рассматривают как активный двухполюсник А (эквивалентный генератор) (см. рис.1, а) со схемой замещения на рис. 1,б.
Совершенно очевидно, что постоянная времени здесь для цепей с индуктивным элементом определяется, как:
и с емкостным, как:
где — входное сопротивление цепи по отношению к зажимам 1-2 подключения ветви, содержащей накопитель энергии.
Например, для напряжения на конденсаторе в цепи на рис. 2 можно записать
где в соответствии с вышесказанным
Переходные процессы при подключении последовательной R-L-C-цепи к источнику напряжения
Рассмотрим два случая:
Согласно изложенной в предыдущей лекции методике расчета переходных процессов классическим методом для напряжения на конденсаторе в цепи на рис. 3 можно записать
Тогда для первого случая принужденная составляющая этого напряжения
Характеристическое уравнение цепи
решая которое, получаем
В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей:
1. или , где — критическое сопротивление контура, меньше которого свободный процесс носит колебательный характер.
2. — предельный случай апериодического режима.
В этом случае и
3. — периодический (колебательный) характер переходного процесса.
В этом случае и
где — коэффициент затухания; — угловая частота собственных колебаний; — период собственных колебаний.
Для апериодического характера переходного процесса после подстановки (2) и (3) в соотношение (1) можно записать
Для нахождения постоянных интегрирования, учитывая, что в общем случае и в соответствии с первым законом коммутации , запишем для t=0 два уравнения:
решая которые, получим
Тогда ток в цепи
и напряжение на катушке индуктивности
На рис. 4 представлены качественные кривые , и , соответствующие апериодическому переходному процессу при .
Для критического режима на основании (2) и (4) можно записать
Для колебательного переходного процесса в соответствии с (2) и (5) имеем
Для нахождения постоянных интегрирования запишем
На рис. 5представлены качественные кривые и , соответствующие колебательному переходному процессу при .
При подключении R-L-C-цепи к источнику синусоидального напряжения для нахождения принужденных составляющих тока в цепи и напряжения на конденсаторе следует воспользоваться символическим методом расчета, в соответствии с которым
Здесь также возможны три режима:
| 1. ; | 2. | 3. |
Наибольший интерес представляет третий режим, связанный с появлением во время переходного процесса собственных колебаний с частотой . При этом возможны, в зависимости от соотношения частот собственных колебаний и напряжения источника, три характерные варианта: 1 — ; 2 — ; 3 — , — которые представлены на рис. 6,а…6,в соответственно.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
- Как можно определить постоянную времени в цепи с одним накопителем энергии по осциллограмме тока или напряжения в какой-либо ветви?
- Определить, какой процесс: заряд или разряд конденсатора в цепи на рис. 2 – будет происходить быстрее?
- Влияет ли на постоянную времени цепи тип питающего устройства: источник напряжения или источник тока?
- В цепи на рис. 2 , С=10 мкФ. Чему должна быть равна индуктивность L катушки, устанавливаемой на место конденсатора, чтобы постоянная времени не изменилась?
- Как влияет на характер переходного процесса в R-L-C-контуре величина сопротивления R и почему?
- Определить ток через катушку индуктивности в цепи на рис. 7, если ; ; ; ; .
Определить ток в ветви с конденсатором в цепи на рис. 8, если ; ; ; .Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать
RC-цепи, 5 самых ходовых схем фильтров и их простой рассчет
RC-цепь, такое частое явление радиоэлектроники. Такие фильтры стоят повсюду. Понимание того, как какой фильтр влияет на форму АЧХ сигнала во многом определяет правильность чтения всей электронной схемы. В статье собраны 5 основных RC-фильтров, приведены их АЧХ и упрощенные формулы расчета.
В ранние годы развития радиоэлектроники для воздействие на Амплитудно — Частотную Характеристику (АЧХ) сигнала в основном применялись LC — фильтры, т.е. фильтры состоящие из катушки индуктивности и конденсатора. Со временем им на смену пришла RC-цепь, которая была плотно взята в оборот радиоэлектроникой ввиду меньшей стоимости и габаритов.
Конечно, фильтры на RC-цепях не могут полностью вытеснить LC собратьев. Например в фильтрах для АС предпочтительнее использование LC-фильтров. Но практически во всей маломощной электронике главенствуют именно RC-цепи. Например двойная RC-цепь в фильтре RIAA-корректора.
Интересным вариантом избавления от катушек являются фильтры на гираторах, где посредством конденсатора и операционного усилителя эмитируется работа катушки.
Видео:ТОЭ79 Переходные процессы. Второй способ создания характеристического уравнения электрической цепи.Скачать
Постоянная времени RC — RC time constant
Постоянная времени RC
, также называемая тау, постоянная времени (в секундах ) RC-цепи , равна произведению сопротивления цепи (в омах ) на емкость цепи (в фарадах ), т. Е.
τ знак равно р C [секунды]
Это время, необходимое для зарядки конденсатора через резистор от начального напряжения заряда, равного нулю, до примерно 63,2% от значения приложенного напряжения постоянного тока или для разряда конденсатора через тот же резистор примерно до 36,8% от его начального значения. напряжение заряда. (Эти значения получены из математической константы e
: и .) Следующие формулы используют ее, принимая постоянное напряжение, приложенное последовательно к конденсатору и резистору, для определения напряжения на конденсаторе в зависимости от времени: 63,2 % знак равно 1 — е — 1 >
Видео:Пример 7 | Классический метод расчета цепи 1-го порядка с конденсаторомСкачать
Постоянная времени электрической цепи — что это такое и где используется
Природе свойственны периодические процессы: день сменяет ночь, теплое время года сменяется холодным и т. д. Период этих событий почти постоянен и поэтому может быть строго определен. Кроме того, мы вправе утверждать, что приведенные в качестве примера периодические природные процессы не являются затухающими, по крайней мере по отношению к продолжительности жизни одного человека.
Однако в технике, а в электротехнике и в электронике — особенно, далеко не все процессы являются периодическими и незатухающими. Обычно какой-нибудь электромагнитный процесс сначала возрастает, а затем убывает. Часто дело ограничивается лишь фазой начала колебания, которое так и не успевает толком набрать размах.
Сплошь и рядом в электротехнике можно встретить так называемые экспоненциальные переходные процессы, суть которых заключается в том, что система просто стремится придти к какому-то равновесному состоянию, которое в конце концов выглядит как состояние покоя. Такой переходный процесс может быть как нарастающим, так и спадающим.
Внешняя сила сначала выводят динамическую систему из состояния равновесия, а затем не препятствует естественному возврату данной системы к ее исходному состоянию. Эта последняя фаза и есть так называемый переходный процесс, которому свойственна определенная длительность. Кроме того процесс выведения системы из равновесия также является переходным процессом с характерной длительностью.
Так или иначе, постоянной времени переходного процесса мы называем его временную характеристику, определяющую время, через которое некоторый параметр данного процесса изменится в «е» раз, то есть увеличится или уменьшится примерно в 2,718 раз по сравнению с состоянием, принятым за исходное.
Рассмотрим для примера электрическую цепь, состоящую из источника постоянного напряжения, конденсатора и резистора. Подобного рода цепь, где резистор включен последовательно с конденсатором, называется интегрирующей RC-цепью.
Если в начальный момент времени подать на такую цепь питание, то есть установить на входе некоторое постоянное напряжение Uвх, то Uвых — напряжение на конденсаторе, начнет по экспоненте нарастать.
Через время t1 напряжение на конденсаторе достигнет 63,2% от напряжения на входе. Так вот, промежуток времени от начального момента до t1 – это и будет постоянная времени данной RC-цепи.
Данную константу цепи называют «тау», она измеряется в секундах, а обозначают ее соответствующей греческой буквой. Численно для RC-цепи она равна R*C, где R выражается в омах, а С — в фарадах.
Видео:ТОЭ 78. Переходные процессы в электрических цепях, составление характеристических уравнений 1 способСкачать
Портал ТОЭ
6.2 Классический метод расчёта переходных процессов
Анализ переходного процесса в линейной цепи с сосредоточенными параметрами R , L , C (рис. 6.2 ) сводится к решению линейных неоднородных уравнений, выражающих законы Кирхгофа.
где i ( t ) – переходный ток.
Дифференцированием приводим это уравнение к неоднородному дифференциальному уравнению 2-го порядка:
Порядок дифференциального уравнения определяется числом накопителей энергии в цепи.
Решение дифференциального уравнения:
где i пр ( t ) – частное решение неоднородного уравнения, принуждённая составляющая, ток в установившемся режиме, когда переходный процесс закончен (при t = ∞ );
i св ( t ) – общее решение однородного уравнения, свободная составляющая, ток во время переходного процесса, возникающий вследствие изменения электрических и магнитных полей.Таким образом здесь используется метод наложения. Физически существует только i ( t ) , а разложение его на i пр и i св является математическим приёмом, облегчающим расчёт переходного процесса.
Расчёт принуждённой составляющей сводится к расчёту по известным методам установившегося значения искомой величины в схеме после коммутации.
Для расчёта свободной составляющей следует найти корни характеристического уравнения p k и n постоянных интегрирования A k .
Если характеристическое уравнение
имеет n различных корней p k ( k = 1 , 2 , … ,n ) , то
Корню p k кратности m k ≥ 1 соответствует слагаемое свободной составляющей вида
Чтобы определить постоянные интегрирования A k , необходимо знать значения искомой величины и всех её производных до ( n − 1) порядка включительно в момент времени t = 0+ . Для их определения используются законы коммутации.
Составление характеристического уравнения
- Составляем уравнение электрического состояния цепи для свободного режима (т.е. при устранении вынужденной (принуждающей) силы). Это соответствует схеме с исключёнными источниками – источники ЭДС закорачиваются, ветви с источниками тока размыкаются.
Например для рис. 6.3 :
- Характеристическое уравнение получается приравниванием нулю определителя контурной ℤ (K) ( p ) или узловой Y (У) ( p ) матрицы. При составлении этих матриц сопротивление индуктивности (ёмкости) считают равным pL m (1 ∕pC m ) :
- Характеристическое уравнение получается при Z вх ( p ) = 0 ,Y вх ( p ) = 0 ,
где Z вх ( p ) – входное сопротивление схемы относительно двух зажимов, получающихся в результате размыкания любой ветви схемы;
Y вх ( p ) – входная проводимость схемы относительно произвольной пары узлов схемы. - Основытеории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретическиеосновы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
- Чем обусловлены переходные процессы?
- Как определяется порядок дифференциального уравнения, описывающего переходный процесс?
- Для каких цепей применим классический метод расчета переходных процессов?
- Доказать законы коммутации:
и
— с энергетических позиций.
- В каких цепях и почему возможен колебательный процесс?
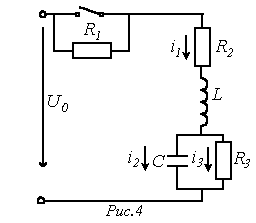
- Определить величину токов
и напряжений
на конденсаторе и
на катушке индуктивности в момент коммутации в цепи на рис. 4, если
.
Корни характеристического уравнения – собственные частоты цепи, т.к. они определяют характер свободных процессов.
Степень характеристического уравнения может быть определена по электрической схеме без составления уравнения: она равна числу основных независимых начальных условий в послекоммутационной схеме после максимального её упрощения и не зависит от числа ЭДС в схеме.
Упрощение заключается в том, что последовательно и параллельно соединённые реактивные элементы должны быть заменены эквивалентными.
Рассмотрим схему на рис. 6.4 . Три реактивных элемента в упрощённой схеме определяют три независимых начальных условия, т.е. порядок характеристического уравнения равен трём.
Свободный процесс происходит в цепи, освобождённой от источников энергии, поэтому свободные токи не могут протекать сколь угодно долго в цепи, где есть активные элементы. Свободные токи должны затухать, в связи с этим действительные части корней p k характеристического уравнения должны быть отрицательными.
- Так, при наличии одного корня p = − a
Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Корни характеристического уравнения. Постоянная времени
Выражение свободной составляющей 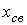
Таблица 3. Выражения свободных составляющих общего решения
| Вид корней характеристического уравнения | Выражение свободной составляющей |
Корни 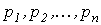 вещественные и различные вещественные и различные | 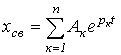 |
Корни 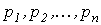 вещественные и вещественные и 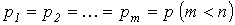 | 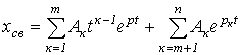 |
Пары комплексно-сопряженных корней 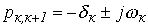 | 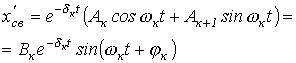 |
Необходимо помнить, что, поскольку в линейной цепи с течением времени свободная составляющая затухает, вещественные части корней характеристического уравнения не могут быть положительными.
При вещественных корнях 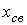
Поскольку физически колебательный процесс связан с периодическим обменом энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, комплексно-сопряженные корни могут иметь место только для цепей, содержащих оба типа накопителей. Быстроту затухания колебаний принято характеризовать отношением
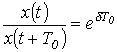
которое называетсядекрементом колебания,или натуральным логарифмом этого отношения
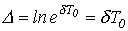
называемым логарифмическим декрементом колебания, где 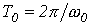
Важной характеристикой при исследовании переходных процессов является постоянная времени t, определяемая для цепей первого порядка, как:
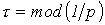
где р – корень характеристического уравнения.
Постоянную времени можно интерпретировать как временной интервал, в течение которого свободная составляющая уменьшится в е раз по сравнению со своим начальным значением. Теоретически переходный процесс длится бесконечно долго. Однако на практике считается, что он заканчивается при
Литература
Контрольные вопросы
 | Ответ: 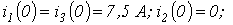 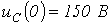 ; ; 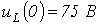 |
Дата добавления: 2015-04-19 ; просмотров: 916 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
🔥 Видео
Электротехника. Переходные процессы в электрических цепях. Классический метод часть 1"Скачать

Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

Пример 5 | Классический метод расчета цепи первого порядка с катушкойСкачать

Расчет цепи при t(0+)│Зависимые начальные условия │КЛАССИЧЕСКИЙ МЕТОДСкачать

Пример 6 | Классический метод расчета цепи первого порядка с конденсаторомСкачать

Лекция 091-6. Расчет переходных процессов классическим методом. Нахождение постоянных интегрированияСкачать

Расчет переходных процессов классическим методомСкачать

ТОЭ Ч2 классический метод расчета ПП лк №10 часть2Скачать

Что такое "уравнение времени"?Скачать

1 6 2 Общий подход к анализу переходных процессовСкачать

Электротехника. Переходные процессы часть 4Скачать

Переходные процессы. Расчет RL цепи с Двойной коммутацией. График переходного процессаСкачать





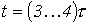
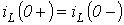 и
и 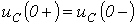 — с энергетических позиций.
— с энергетических позиций.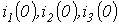 и напряжений
и напряжений 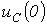 на конденсаторе и
на конденсаторе и 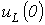 на катушке индуктивности в момент коммутации в цепи на рис. 4, если
на катушке индуктивности в момент коммутации в цепи на рис. 4, если 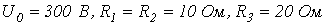 .
.