ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ
|
1. Исследовать одноконтурную САУ при заданных передаточных функциях составляющих ее элементов.
|
|
|
|
Рис. 1.1 Структура одноконтурной САУ
регулятора, исполнительного механизма, объекта регулирования, датчика соответственно.
φ, φ3, φg — заданное, действительное и измеренное значения регулируемой величины соответственно;
λ — возмущающее воздействие.
При выполнениии задания вид передаточных функций определяют по последней цифре номера зачетной книжки, а значения коэффициентов по предпоследней.
Таблица 1.1
Значения передаточных функций звеньев САУ
| №/пп | Wн(p) | Wc(p) | Wp(p) | Wo(p) |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  |
Таблица 1.2
Значения коэффициентов передаточных функций
| № | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Kо | 1,6 | 1,1 | 1,8 | 2,1 | 1,6 | 1,9 | 2,8 | 3,2 | 1,4 | 0,9 |
| То | ||||||||||
| Т | ||||||||||
| Kр | ||||||||||
| Тн | ||||||||||
| Тg | ||||||||||
| Kс | 0,1 | 0,4 | 0,3 | 0,7 | 0,9 | 1,8 | 1,2 | 0,9 | 2,0 | 1,7 |
| Тс | ||||||||||
| Ни | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 |
| Т1 |
1.1. Рассчитать передаточные функции разомкнутой и замкнутой САУ по каналам возмущающего воздействия λ и задания φ3.
1.2. Выполнить анализ устойчивости замкнутой системы с применением алгебраического и частотного критериев устойчивости.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Передаточные функции соединения звеньев САУ

Рис. 2.1 Последовательное соединение звеньев САУ
Результирующая передаточная функция равна отношению операторного изображения выходной величины к операторному изображению входной при нулевых начальных условиях

При параллельном включении звенья имеют общий вход, а выходной сигнал цепочки равен сумме выходных сигналов отдельных звеньев.
Рис. 2.2 Параллельное соединение звеньев САУ
Для этой схемы результирующая передаточная функция равна сумме передаточных функций отдельных звеньев и имеет вид:

Для замкнутых САУ характерно так называемое встречно-параллельное включение или соединение с обратной связью.
Рис. 2.3 Соединение с обратной связью
В этом случае результирующая передаточная функция равна дроби, числитель которой передаточная функция прямой связи, а знаменатель — единица плюс или минус передаточная функция разомкнутого контура. Знак плюс соответствует отрицательной, а минус — положительной обратной связи.

Под прямой связью понимается передаточная функция между искомыми переменными по направлению прохождения сигнала без учета главной обратной связи. В рассматриваемой схеме передаточная функция прямой связи между λ и φ равна Wo(p), а между φ3 и φ – Wp(p)Wc(p)Wo(p). Передаточная функция прямой связи между φ3 и ε равна единице. Поэтому
где 


Выполняя несложные преобразования, определим

Для замкнутой системы передаточная функция по каналу 

Характеристическое уравнение замкнутой САУ
Для анализа устойчивости САУ необходимо знать характеристическое уравнение замкнутой системы. Оно получается, если приравнять знаменатель передаточной функции замкнутой системы нулю, т.е.
Известно правило, что при известной передаточной функции разомкнутой системы, характеристическое уравнение замкнутой системы получают сложением полиномов числителя и знаменателя и приравниванием полученной суммы нулю, A(p)+B(p)=0
В рассматриваемом примере (2.4)
Сложив их, получают в общем виде характеристическое уравнение замкнутой системы:
- 2. Математическое описание систем автоматического управления
- 2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
- 2.2. Линеаризация уравнений динамики САУ (САР)
- Пример
- 2.3. Классический способ решения уравнений динамики
- Пример
- Курсовая работа: Системы автоматического управления
- 🎬 Видео
Видео:Теория автоматического управления. Лекция 8. Основы устойчивостиСкачать

2. Математическое описание систем автоматического управления
Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:
2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики
Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.
Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
Видео:Теория автоматического управления. Лекция 7. Типовые звенья САУСкачать

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.
На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).
При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.
Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др
Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).
где: — стационарные значения входного и выходного воздействий;
— отклонения от станционара, соотвесвенно.
В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.
Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:
где, m — масса тела, Fj — все силы воздействующие на тело (поршень демпфера)
Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:
где — сила тяжести;
— сила сопротивления пружины,
— сила вязконо трения (пропорциональна скорости поршеня)
Размерности сил и коэффициентов, входящих в уравнение (2.1.2):
Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть
перейдем к отклонениям от стационарного состояния:
Пусть при t>0 . Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:
если , то уравнение принимает вид:
Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).
Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:
тогда, разделив на k, имеем:
Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!
«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:
Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [];
— коэффициент в правой части (): [
].
Тогда уравнение (2.1.6) можно записать в операторной форме:
, что эквивалентно
где: — оператор диффренцирования;
-линейный дифференциальный оператор;
— линейный дифференциальный оператор, вырожденный в константу, равную
.
Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.
Введем новые нормированные (безразмерные) переменные:
Подставляя эти соотношения в уравнение (2.1.2), имеем:
Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие , и, разделив на
, получаем:
где: — коэффициент усиления, причем безразмерный.
Проверим размерность коэффициента
Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.
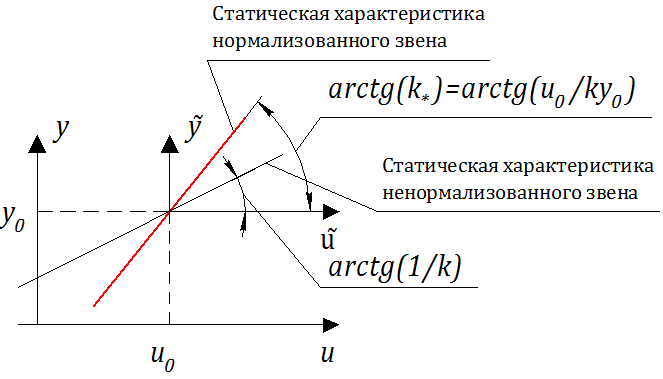
На рис. 2.1.4 представлены статические характеристики для механического демпфера:
Процедура нормировки отклонений позволяет привести уравнения динамики к виду:
где дифференциальные операторы.
Если дифференциальные операторы — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).
А если – нелинейные дифференциальные операторы, или
, то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).
Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»
Видео:Теория автоматического управления. Лекция 19. Критерий РаусаСкачать

2.2. Линеаризация уравнений динамики САУ (САР)
Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:
- Нелинейностью статической характеристики.
- Нелинейностью динамических членов в уравнениях динамики.
- Наличием в САУ принципиально нелинейных звеньев.
Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).
Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N0 Рис. 2.2.1 – Пример изменения мощности реактора
Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:
Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:
Перенесем в левую часть уравнения и запишем уравнение в виде%
где -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.
Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:
Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния .
Напомним, что разложение в ряд Тейлора трактуется следующим образом: если , то «простое» разложение функции в ряд Тейлора в окрестности точки
будет выглядеть так:
C учетом вышеприведенного разложение принимает вид:
Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:), оставим в разложении только члены первого порядка малости (линейные). Поскольку
, получаем:
Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:
Коэффициенты — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.
В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:
где – оператор дифференцирования;
— линейный дифференциальный оператор степени n;
— линейный дифференциальный оператор степени m, причем обычно порядок оператора
выше порядка оператора
:
Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.
Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).
Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) и выполнив некоторые преобразования, получаем:
Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>
Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на
, то уравнение принимает вид:
или в операторном виде:
Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.
Пример
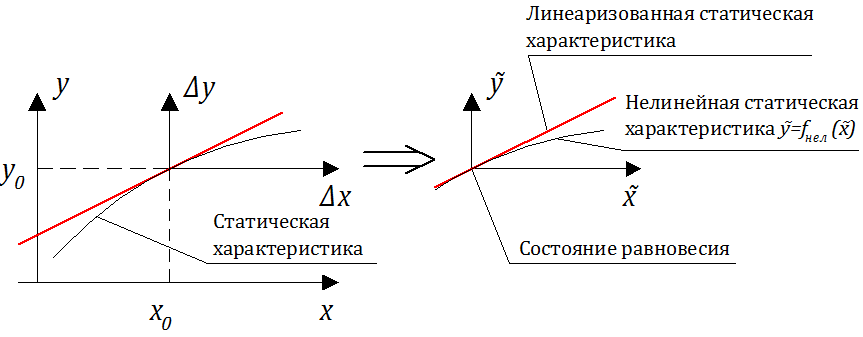
Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x0, y0), если полное уравнение динамики имеет вид:
Нелинейность полного уравнения динамики проявляется в следующем:
• во-первых, в нелинейности статической характеристики:
• во-вторых, слагаемое в левой части — чисто нелинейное, так как действие умножения является нелинейным.
Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x0, y0) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.
Преобразования выполним в следующей последовательности:
- Перейдем к безразмерным переменным (нормализованным);
- Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.
Перейдем к новым безразмерным переменным:
Заметим, что: .
Подставляя значения x(t) и y(t) в исходное уравнение:
Удаляем полученного уравнения уравнения стационара: , а так же пренебрегая слагаемыми второго прядка малости:
, получаем следующее уравнение:
Вводим новые обозначения:
Получаем уравнения в «почти» классическом виде:
Если в правой части вынести за общую скобку и разделить все уравнение на
, то уравнение (линеаризованное) принимает вид:
Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).
Видео:Теория автоматического управления. Лекция 23. Корневой метод Соколова Т.Н.Скачать

2.3. Классический способ решения уравнений динамики
Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.
Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:
Переходя к полной символике, имеем:
Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.
Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).
Требуется найти y(t) при известных начальных условиях.
где: — решение однородного дифференциального уравнения
y_(t) $inline$ — частное решение. $inline$
Будем называть решение однородного дифференциального уравнения , собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).
Вторую составляющую решения (2.3.3) будем называть , вынужденным, так как эта часть решения определяется внешним воздействием
, поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:
Напомним этапы решения:
1) Если имеется уравнение вида , то сначала решаем однородное дифференциальное уравнение:
2) Записываем характеристическое уравнение:
3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения
4) Тогда собственное решение записывается в виде:
если среди нет повторяющихся корней (кратность корней равна 1).
Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:
Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:
5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…
Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. .
6) Суммируя полученные составляющие (собственную и вынужденную), имеем:
7) Используя начальные условия (t = 0), находим значения постоянных интегрирования .
Обычно получается система алгебраических уравнений.
Решая систему, находим значения постоянных интегрирования
Пример
Найти аналитическое выражение переходного процесса на выходе звена, если
Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем:
тогда:
где — неизвестные (пока) постоянные интегрирования.
По виду временной функции в правой части запишем как:
Подставляя в исходное уравнение, имеем:
Суммируя , имеем:
Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального условия имеем:
Решая систему уравнений относительно и
, имеем:
Тогда окончательно:
Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:
Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).
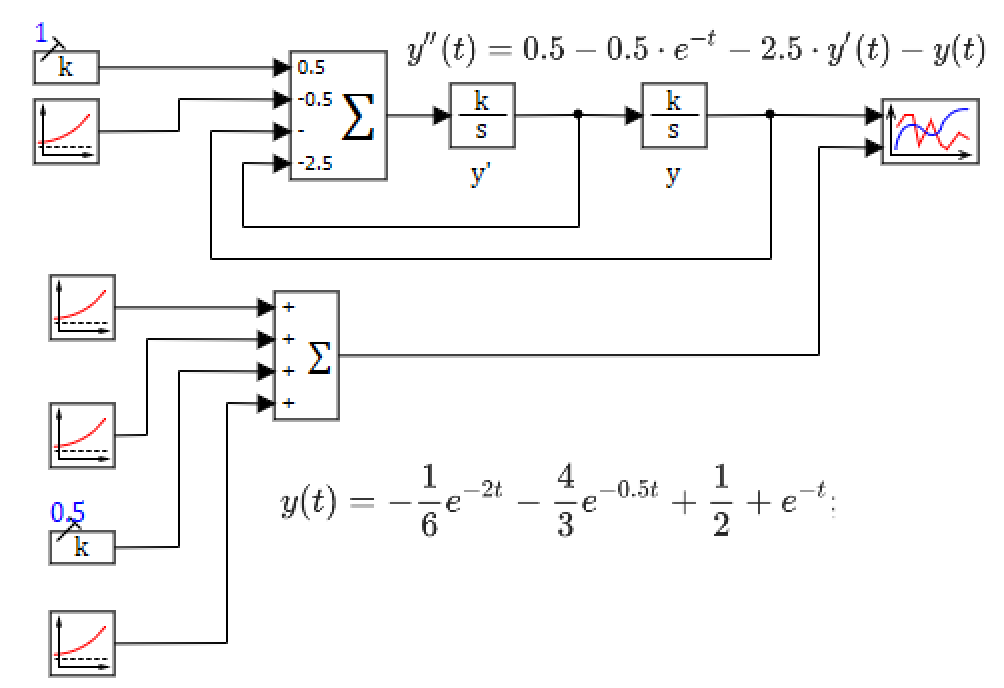
Рис. 2.3.1 – структурная схема для проверки решения
На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).
Видео:Теория автоматического управления. Лекция 6. Структурные схемы САУСкачать
Курсовая работа: Системы автоматического управления
| Название: Системы автоматического управления Раздел: Рефераты по коммуникации и связи Тип: курсовая работа Добавлен 02:17:56 08 апреля 2010 Похожие работы Просмотров: 1936 Комментариев: 19 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||
| a1 | 0 | b2 | 0.042 | c1 | 0.2 | d2 | 0 | g | 1,8…8 |
| a0 | 6 | b1 | 1,864 | c0 | 3 | d1 | 0.01 | z | 0…-9 |
Передаточные функции звеньев:

Уравнение замкнутой системы имеет вид:

где 


Расчет коэффициента усиления К САУ (рис.1) проводим для определения его значения, при котором суммарная статическая ошибка ε не будет превышать 

Так как кроме коэффициента усиления на величину ошибки влияют значения управляющего и возмущающего воздействий, причем наибольшая величина ε достигается при действии на систему минимального управляющего воздействия 
где y – выходная переменная.
Значение выходной переменной y определяется реакцией САУ на сумму управляющего и возмущающего воздействий. Поэтому:

Здесь Kg , Kz – представляют собой суммарные коэффициенты усиления соответственно задающего и возмущающего воздействия и могут быть определены из передаточных функций системы, найденных по задающему и возмущающему воздействиям.

Подставляя значение y из выражения (3) в выражение (1) и решая полученное уравнение относительно K , входящего в выражения для Kg и Kz , определяют коэффициент усиления САУ (рис.1), при котором суммарная статическая ошибка ε не превышает заданного значения.

Суммарная статическая ошибка

2. Построение внешних статических характеристик
Построим внешние статические характеристики для замкнутой САУ в заданном диапазоне. Для этого построим график функции



т.е. 
Берем три значения 
Получаем уравнение прямой для каждого значения y.
 |  | |
| g=1.8 | y=1.797637 | y=1.7622 |
| g=4 | y=3.99475 | y=3.959312 |
| g=8 | y=7.9895 | y=7.954063 |
Рис. 2. Графики внешних статических характеристик замкнутой САУ:
а) – значение задающего воздействия g=8
б) – значение задающего воздействия g=4
в) – значение задающего воздействия g=1.8
3. Расчёт корней характеристического уравнения
Для САУ с отрицательной обратной связью передаточная функция имеет следующий вид:
Характеристическое уравнение передаточной функции:
Найдём корни характеристического уравнения:
Решая кубическое уравнение в среде MatCad получаем корни:
Предварительно: САУ устойчива, т.к. вещественная часть комплексно сопряженных корней отрицательна. Переходная характеристика является сходящейся, с частотой



коэффициент затухания δ=-64.8.
4. Построение частотных характеристик САУ
Рассчитаем и построим логарифмические амплитудную частотную (ЛАЧХ) и фазовую частотную (ЛФЧХ) характеристики замкнутой системы.
Передаточная функция замкнутой системы:
Получим выражение для комплексно-частотной функции:
Вещественная частотная функция:
Мнимая частотная функция:
На практике АЧХ и ФЧХ изображают в логарифмическом масштабе. Это позволяет упростить расчет и анализ характеристик.
ЛАЧХ – логарифмическая амплиудно-частотная характеристика.
ЛФЧХ – логарифмическая фазо-частотная характеристика.
Рис.3. Логарифмические амплитудно-частотная и частотно-фазовая
Частота при которой 
Из графиков видно, что запас устойчивости по амплитуде бесконечен, т.к. ЛФЧХ не пересекает угол -180˚.
Запас устойчивости по фазе имеет конечное значение (180˚-159˚=21˚).
Согласно критерию Найквиста, если система устойчива в разомкнутом состоянии, то для устойчивости соответствующей замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты от 0 до ¥ не охватывала точку (–1;j0) на комплексной плоскости.
Как видим из граф. что по Найквисту система устойчива, т.к. точку (-1,j0) АФЧХ данной условно разомкнутой САУ не охватывает.
5. Моделирование переходных характеристик исходной САУ
а) при отсутствии возмущений для граничных значений g
Рис. 5 Переходная характеристика САУ при минимальном задающем воздействии и отсутствии задания.

время переходного процесса: tпп =0.045с
время регулирования tp =0.0051c
при подачи сигналаg =8
Рис. 6 Переходная характеристика САУ при максимальном задающем воздействии и отсутствии задания.

время переходного процесса: tпп =0.045с
время регулирования tp =0.0052с
б)переходный процесс:при действующих максимальных возмущениях для граничных значений g
при подачи сигналаg =1.8 и возмущающем воздействии z=-9
Рис. 7 Переходная характеристика САУ при максимальном возмущающем и минимальном задающем воздействиях

время переходного процесса: tпп =0.045с
время регулирования tp =0.0049c

время переходного процесса: tпп =0.102с,
время регулирования tp =0.0045c,
переходный процесс: при действующих максимальных возмущениях для граничных значений g при подачи сигналаg =8, и возмущающем воздействии z=-9
Рис. 8 Переходная характеристика САУ при максимальном возмущающем и максимальном задающем воздействиях

время переходного процесса: tпп =0.045с
время регулирования tp =0.0049c

время переходного процесса: tпп =0.14с
время регулирования tp =0.0043c
6. Проверка САУ на устойчивость
Проверка на устойчивость замкнутой САУ производится с помощью алгебраического критерия Гурвица:
По Гурвицу: передаточная функция замкнутой системы в динамическом режиме имеет вид:
Характеристическое уравнение имеет вид:

Обозначим:
Составляем определитель Гурвица:

7 Синтез корректирующего устройства, обеспечивающего настройку исходной системы на симметричный оптимум
Синтез корректирующего устройства проводится для обеспечения оптимальных показателей качества регулирования САУ путем настройки ее на симметричный оптимум.
Передаточная функция разомкнутой системы:
Коэффициент демпфирования второго звена
По средствам пакета Mathсad найдем корни характеристического уравнения:

Где
Желаемая передаточная функция разомкнутой системы, настроенной на симметричный оптимум, имеет вид:
где 
Обозначив как 

Рис. 9. Структурная схема скорректированной разомкнутой САУ
Параметры корректирующих звеньев:
1. Пропорциональное звено К=199.5
2. Интегрирующие звенья



3. Дифференцирующее звено

Рис.10. Модель скорректированной САУ в Matlab
a) минимальное значение управляющего (g=1.8) и отсутствие возмущающего (z=0) воздействий: g =1.8
Рис.11. Переходная характеристика скорректированной САУ при минимальном задающем и отсутствии возмущающего воздействия (g=1.8 z=0)
время переходного процесса:
б) максимальное значение управляющего (g=8) и отсутствие возмущающего (z=0) воздействий: g =8
Рис.12. Переходная характеристика скорректированной САУ при максимальнм задающим и отсутствии возмущающего воздействия (g=8 z=0)
время переходного процесса:
в) минимальное значение управляющего (g=1.8) и максимальное возмущающее (z=9) воздействий g=8
Рис.13. Переходная характеристика скорректированной САУ при минимальном задающим и максимальным возмущающим воздействии (g=1.8 z=-9)
перерегулирование:
время переходного процесса:
г) максимальное значение управляющего (g=8) и максимальное возмущающее (z=9) воздействий g=8
Рис.14. Переходная характеристика скорректированной САУ при максимальном задающим и максимальным возмущающим воздействии (g=8 z=-9)
время переходного процесса:
Рис.15. АФЧХ разомкнутой скорректированной САУ
Как видно из рисунка характеристика не охватывает точку [-1:0]. Из этого следует что разомкнутая, а следовательно соответственно, замкнутая САУ устойчива (по Найквисту).
Рис.16. ЛАЧХ и ЛФЧХ разомкнутой скорректированной САУ
Запас устойчивости по амплитуде определяется величиной допустимого подъема ЛАЧХ, при котором система окажется на грани устойчивости. Из рисунка видно что запас по амплитуде бесконечен т.к. ЛФЧХ не достигает критической фазы 
Запас устойчивости по фазе определяется величиной избытка фазы, на который должен вырасти запаздывание САУ при частоте среза, чтобы САУ оказалась на границе устойчивости:
8. Оптимизация САУ
Объект управления содержит в себе звено второго порядка, которое на практике реализовать достаточно трудно. Следовательно, адекватно было бы упростить объект управления, понизив его порядок. Передаточная функция ОУ имеет вид:
— форсирующую постоянную времени
— три инерционные постоянные времени:
Так как процесс определяет инерционная составляющая равна Ти2 = 1.852, то можно пренебречь форсажом 0.2 и малыми инерционными составляющими Ти1 = 0.023, Ти3 = 0.01. т.к. они лежат справа от рабочей полосы частот, получим ОУ вида
Для данного ОУ получим регулятор:

где 

Рис.17. Схема САУ с упрощенным ОУ упрощенным регулятором
Рис.18. ЛАЧХ и ЛФЧХ разомкнутой системы с упрощенным ОУ упрощенным регулятором
Запас устойчивости по амплитуде определяется величиной допустимого подъема ЛАЧХ, при котором система окажется на грани устойчивости. Из рисунка видно что запас по амплитуде бесконечен т.к. ЛФЧХ не достигает критической фазы 
Запас устойчивости по фазе определяется величиной избытка фазы, на который должен вырасти запаздывание САУ при частоте среза, чтобы САУ оказалась на границе устойчивости:
Рис.19. Переходная характеристика скорректированной САУ с упрощенным ОУ при минимальном задающем и отсутствии возмущающего воздействия (g=1.8 z=0)

время переходного процесса:
Рис.10. Модель скорректированной САУ в Matlab
Рис.20. ЛАЧХ и ЛФЧХ разомкнутой скорректированной САУ
Рис.21. Переходная характеристика скорректированной САУ при минимальном задающем и отсутствии возмущающего воздействия (g=1.8 z=0)
время переходного процесса:
В рамках курсовой работы был проведен синтез САУ с заданным качеством. Был рассчитан коэффициент передачи исходной САУ с заданной статической ошибкой и с учетом влияния задающего и возмущающего воздействий. Были рассчитаны и построены статические внешние характеристики замкнутой САУ.
По характеристическому уравнению предварительно было определено, что исходная САУ устойчива, а график переходной характеристики представляет собой сходящиеся колебания. Для условно разомкнутой САУ были построены логарифмические характеристики (ЛАЧХ и ЛФЧХ). Так как САУ, по предварительной оценке, неустойчива, то нельзя говорить о параметрах запаса САУ по фазе и амплитуде.
По критерию Гурвица, после составления матрицы третьего порядка, было определено, что САУ устойчива. Проверку правильности решения матрицы третьего порядка провели на основе моделирования в пакете Mathlab критерия Найквиста. Был проведен синтез корректирующего устройства, обеспечивающего устойчивость исходной САУ и ее настройка на симетричный оптимум.
Были смоделированы, в пакете Mathlab, переходные процессы скорректированной САУ и определены время переходных процессов и величина перерегулирования.
На основе ЛАЧХ и ЛФЧХ скорректированной САУ был определен запас по фазе и амплитуде.
1. Теория автоматического управления: Учеб. для вузов. – Ч. 1. Теория линейных систем автоматического управления / Под ред. А. А. Воронова. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1986.
2. Иванов Е. А., Сильченкова В. В. Исследование качества и синтез линейных систем автоматического управления: Учеб. пособие по курсу «Теория автоматического управления». – М.: МИЭТ, 1982.
3. Иванов Е. А., Сильченкова В. В. Линейные системы автоматического управления: Учеб. пособие. – М.: МИЭТ, 1980.
🎬 Видео
Теория автоматического управления. Лекция 10. Критерий МихайловаСкачать

1) ТАУ (Теория автоматического управления) для чайников. Часть 1: основные понятия...Скачать

Теория автоматического регулирования. Лекция 3. Временные характеристики САУСкачать

Лекция 1 | Теория автоматического управленияСкачать

Устойчивость систем по критерию Гурвица ПримерыСкачать

Теория автоматического управления. Лекция 12. D-разбиениеСкачать

Теория автоматического управления. Лекция 7. Дискретные САУ. Алгебраический критерий устойчивостиСкачать

Частотные характеристики | Утро с теорией управления, лекция 5Скачать

Преобразование структурных схем систем управленияСкачать

№12. Условия устойчивости линейных систем автоматического управления. Критерий устойчивости Рауса.Скачать

Теория автоматического управления. Лекция 14. Косвенные показатели качества САУСкачать

Основы теории автоматического управленияСкачать

Теория автоматического управления. Лекция 20. Критерий Льенара - ШипараСкачать