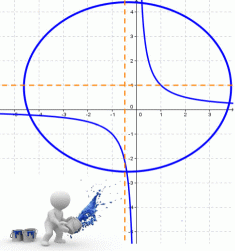
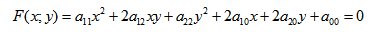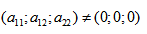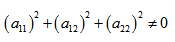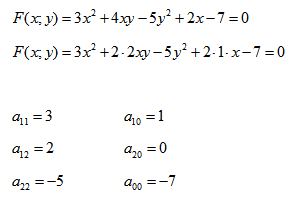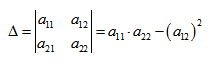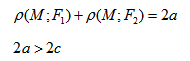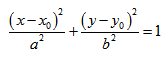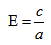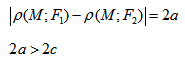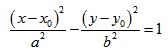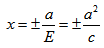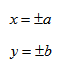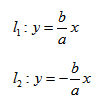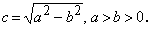- Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:
- Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.
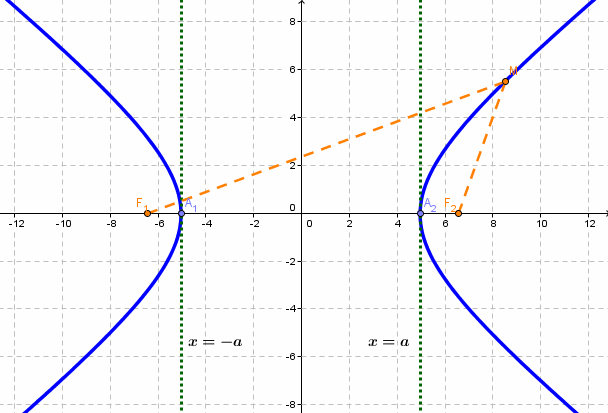
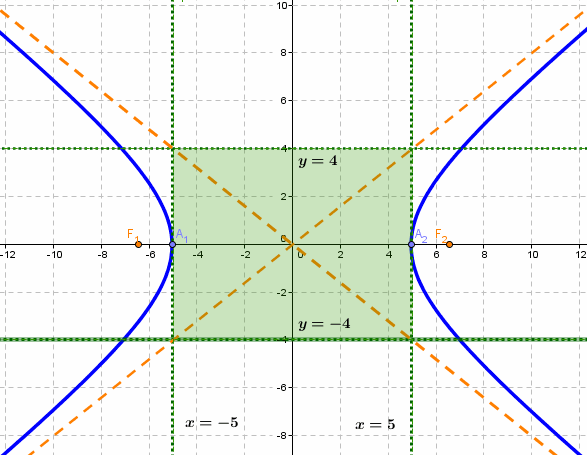
- Гипербола — множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками.
- Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
- Кривые второго порядка — определение и построение с примерами решения
- Эллипс
- Гипербола
- Кривые второго порядка на плоскости
- Теоремы, связанные с кривыми второго порядка
- 🎬 Видео
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:
Видео:Кривые второго порядкаСкачать

Видео:Лекция 31.2. Кривые второго порядка. Гипербола.Скачать

Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.
Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

или можно встретить следующую форму записи:
Видео:Лекция 31.3. Кривые второго порядка. Парабола.Скачать

К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.
Покажем на примере определение значений коэффициентов.
Рассмотрим кривую второго порядка:
Видео:Видеоурок "Общее уравнение кривой 2 порядка"Скачать

Вычислим определитель из коэффициентов:
Если Δ = 0, кривая второго порядка параболического типа,
если Δ > 0, кривая второго порядка эллиптического типа,
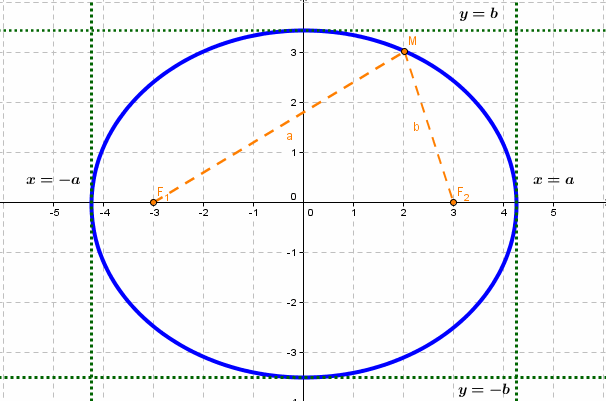
если Δ F1 и F2 — фокусы.
 |
 |
 | 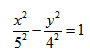 |
Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
F — фокус параболы, f — директриса параболы.
Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Кривые второго порядка — определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Видео:Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 

Точки 
Если а =Ь, то уравнение (7.3) можно переписать в виде:

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 

Число 


Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 







Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Видео:§26 Общее уравнение кривых второго порядкаСкачать

Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 

Точки 



Тогда 




Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 
Легко показать, что уравнение 

и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 

Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию




Видео:53. Приведение общего уравнения кривой к каноническому видуСкачать

Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

Число а называют большей полуосью эллипса, число 
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 

Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:


Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 

В новой системе координат координаты 
Переходя к старым координатам, получим:
Построим график эллипса.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Теоремы, связанные с кривыми второго порядка
Содержание
1.Кривые второго порядка
2.Теоремы, связанные с кривыми второго порядка
Введение
Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.
Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второй космической скорости тело по параболе покинет поле притяжения Земли.
Кривые второго порядка
Кривой 2-го порядка называется линия на плоскости, которая в некоторой декартовой системе координат определяется уравнением
ax2 + 2bxy + cy2 + 2dx + 2ey + f = 0
где a, b, c, d, e, f — вещественные коэффициенты, причем a2 + b2 + c2 ≠ 0 .
Вид кривой зависит от четырёх инвариантов:
инварианты относительно поворота и сдвига системы координат:
инвариант относительно поворота системы координат (полуинвариант):
Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой:
Так, например, невырожденная кривая 

Корни этого уравнения являются собственными значениями вещественной симметричной матрицы и, как следствие этого, всегда вещественны:
Кривые второго порядка классифицируются на невырожденные кривые и вырожденные.
Доказано, что кривая 2–го порядка, определяемая этим уравнением принадлежит к одному из следующих типов: эллипс, гипербола, парабола, пара прямых (пересекающихся, параллельных или совпадающих), точка, пустое множество.
Иными словами, для каждой кривой 2-го порядка (для каждого уравнения) существует такая система координат, в которой уравнение кривой имеет вид:
Эллипс
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная. Отрезки, соединяющие точку эллипса с фокусами, называются фокальными радиусами точки.
Если эллипс описывается каноническим уравнением
где a > 0 , b > 0, a > b > 0 — большая и малая полуоси эллипса, то фокусы эллипса расположены симметрично на оси абсцисс и имеют координаты (−c, 0) и ( c, 0), где
Величина e = c/a называется эксцентриситетом эллипса.
По определению эллипса r1 + r2 = 2a, r1 и r2 − фокальные радиусы, их длины вычисляются по формулам
Если фокусы эллипса совпадают, то эллипс является окружностью.
Гипербола
Гиперболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением
где a > 0, b > 0 — параметры гиперболы.
Это уравнение называется каноническим уравнением гиперболы, а система координат, в которой гипербола описывается каноническим уравнением, называется канонической.
В канонической системе оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии.
Точки пересечения гиперболы с осью OX ( ± a, 0) называются вершинами гиперболы.
С осью OY гипербола не пересекается.
Отрезки a и b называются полуосями гиперболы.
Прямые ay − bx = 0 и ay + bx = 0 — асимптоты гиперболы, при удалении точки гиперблы в бесконечность, соответствующая ветвь гиперболы приближается к одной из асимптот.
Уравнение описывает гиперболу, вершины которой лежат на оси OY в точках (0, ± b).
Такая гипербола называется сопряженной к гиперболе её асимптоты — те прямые ay − bx = 0 и ay + bx = 0. Говорят о паре сопряжённых гипербол.
Парабола
Параболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением
где p > 0 — параметр параболы.
Такое уравнение называется каноническим уравнением параболы, а система координат, в которой парабола описывается каноническим уравнением, называется канонической.
В канонической системе ось абсцисс является осью симметрии параболы, а начало координат — её вершиной.
Уравнения y2 = −2 px, x2 = 2 py, и x2 = −2 py, p > 0, в той же самой канонической системе координат также описывают параболы:
Теоремы, связанные с кривыми второго порядка
Теоремма Паскамля — теорема проективной геометрии, которая гласит, что:
Если шестиугольник вписан в окружность либо любое другое коническое сечение (эллипс, параболу, гиперболу, даже пару прямых), то точки пересечения трёх пар противоположных сторон лежат на одной прямой. Теорема Паскаля двойственна к теореме Брианшона.
Теорема Брианшона является классической теоремой проективной геометрии. Она сформулируется следующим образом:
Если шестиугольник описан около конического сечения, то три диагонали, соединяющие противоположные вершины этого шестиугольника, проходят через одну точку.
В частности, в вырожденном случае:
Если стороны шестиугольника проходят поочерёдно через две данные точки, то три диагонали, соединяющие его противоположные вершины, проходят через одну точку.
Теорема Брианшона двойственна к теореме Паскаля, а её вырожденный случай двойственен к теореме Паппа.
Литература
1. Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64-69.
2. Корн Г., Корн Т. 2.4-5. Характеристическая квадратичная форма и характеристическое уравнение // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64.
3. В.А. Ильин, Э.Г. Позняк. Аналитическая геометрия, гл. 6. М.: «Наука», 1988.
🎬 Видео
Приводим уравнение кривой 2 порядка к каноническому видуСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Характеристическое уравнение в ДУСкачать

Приведение кривой второго порядка к каноническому виду. ПримерСкачать