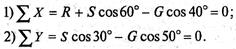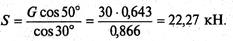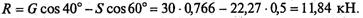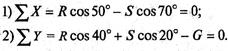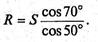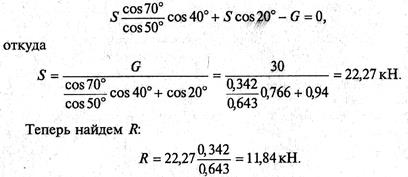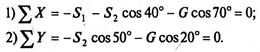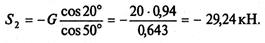| Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |
Видео:Определение реакций опор простой рамыСкачать

Контрольная работа №2
ПО РАЗДЕЛУ «Сопротивление материалов»
Тема 2.2. Расчеты на прочность и жесткость при растяжении и сжатии
Знать порядок расчетов на прочность и жесткость, и расчетные формулы.
Уметь проводить проектировочные и проверочные расчеты на прочность и жесткость при растяжении и сжатии.
где N — продольная сила; А — площадь поперечного сечения.
Удлинение (укорочение) бруса:
Е-модуль упругости; l — начальная длина стержня.
[s] — допускаемый запас Прочность
Условие прочности при растяжении и сжатии:
Примеры расчетов на прочность и жесткость
Пример 1. Груз закреплен на стержнях и находится в равновесии (рис. П6.1). Материал стержней — сталь, допускаемое напряжение 160 МПа. Вес груза 100 кН. Длина стержней: первого — 2 м, второго — 1 м. Определить размеры поперечного сечения и удлинение стержней. Форма поперечного сечения — круг.
1. Определить нагрузку на стержни. Рассмотрим равновесие точки В, определим реакции стержней. По пятой аксиоме статистики (закону действия и противодействия) реакция стержня численно равна нагрузке на стержень.
Наносим реакции связей, действующих в точке В. Освобождаем точку В от связей (рис. П6.1).
Выбираем систему координат так, чтобы одна из осей координат совпала с неизвестной силой (рис. П6.1б).
Составим систему уравнений равновесия для точки В:
Решаем систему уравнений и определяем реакции стержней.
Направление реакций выбрано, верно. Оба стержня сжаты. Нагрузки на стержни: F1 = 57,4 кН; Р2 = 115,5 кН.
2. Определяем потребную площадь поперечного сечения стержней из условий прочности.
Условие прочности на сжатие:
откуда
Стержень 1 (N1 = Рl):
Полученные диаметры округляем.
3. Определяем удлинение стержней
Укорочение стержня 1:
Укорочение стержня 2:
Пример 2. Однородная жесткая плита с силой тяжести 10 кН, нагруженная силой F = 4,5кН и моментом т = 3КН’м, оперта в точке А и подвешена на стержне Ее (рис. П6.2). Подобрать сечение стержня в виде швеллера и определить его удлинение, если длина стержня 1 м, материал — сталь, предел текучести 570 МПа, запас прочности для материала 1,5.
1. Определить усилие в стержне под действием внешних сил. Система находится в равновесии, можно использовать уравнение равновесия для плиты:
RB — реакция стержня реакции шарнира А не рассматриваем,
По третьему закону динамики ре акция в стержне равна силе, действующей от стержня на плиту. Усилие в стержне равно 14кН.
2. По условию прочности определяем потребную величину площади попе речного сечения:
откуда
Допускаемое напряжение для материала стержня
3. Подбираем сечение стержня по ГОСТ (Приложение 1). Минимальная площадь швеллера 6,16 см^2 (№ 5; ГОСТ 8240-89). Целесообразнее использовать равнополочный уголок № 2 (d = 3 мм), площадь поперечного сечения, которого 1,13 см^2 (ГОСТ 8509-86)
4. Определить удлинение стержня:
Задание 1. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение свободного конца бруса. Двухступенчатый стальной брус нагружен силами Р1, Р2; РЗ· Площади поперечных сечений А1 и А2.
Принять
Видео:Определить реакции стержней, удерживающих груз весомСкачать

Примеры выполнения рефератов
Определение равнодействующей системы сил аналитическим способом
Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равнодействующую геометрическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси (рис. 3.4а). Складываем проекции всех векторов на оси х и у (рис. 3.46).
FΣч = Flx + F2x + F3x + F4x; FΣн = Fly + F2y + F3y + F4y;
Модуль (величину) равнодействующей можно найти по известным проекциям:
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующей с осями координат (рис. 3.5).
Условия равновесия плоской системы
сходящихся сил в аналитической форме
Исходя из того, что равнодействующая равна нулю, получим:
Условия равновесия в аналитической форме можно сформулировать следующим образом:
Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.
Система уравнений равновесия плоской сходящейся системы сил:
В задачах координатные оси выбирают так, чтобы решение было наиболее простым. Желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.
Контрольные вопросы и задания
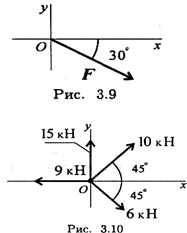
Запишите выражение для расчета проекции силы F на ось Оу (рис. 3.9).
Определите сумму проекций сил системы на ось Ох (рис. 3.10
3. Определите величину силы по известным проекциям:
Fч = 3 kH; Fy = 4 кH.
4. Груз находится в равновесии (рис. 3.11). Какая система уравнений равновесия для шарнира Л записана верно?
При ответе на вопросы 1 и 2 необходимо знать, что в выражение для величины проекции силы на ось подставляется угол между вектором силы и положительной полуосью координат. Не забыть, что определяется алгебраическая сумма.
При ответе на вопрос 4 сначала следует определить возможные направления реакций в стержнях, мысленно убирая по очереди стержни и рассматривая возможные перемещения (см. лекцию 1). Затем записать алгебраические суммы проекций сил на оси Ох и Оу. Полученные уравнения сравнить с приведенными.
Видео:определение реакций в стержнях от действия грузовСкачать

Условия равновесия плоской системы сходящихся сил в аналитической форме
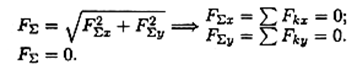 |
Исходя из того, что равнодействующая равна нулю, получим:
Условия равновесия в аналитической форме можно сформулировать следующим образом:
Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.
Система уравнений равновесия плоской сходящейся системы сил:
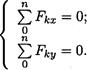 |
В задачах координатные оси выбирают так, чтобы решение было наиболее простым. Желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.
Примеры решения задач
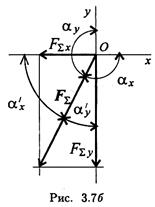
Пример 1. Определить величины и знаки проекций представленных на рис. 3.6 сил.
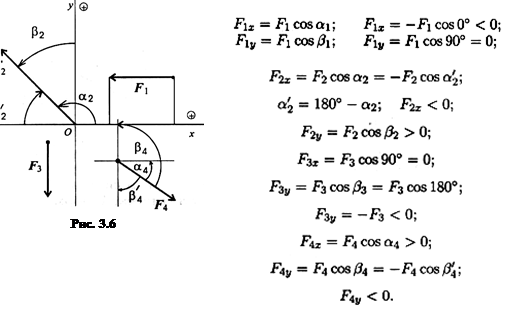 |
Решение
Пример 2. Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом.
Решение
1.
 |
Определяем проекции всех сил системы на Ох (рис. 3.7, а):
Сложив алгебраически проекции, получим проекцию равнодействующей на ось Ох.
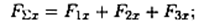 |
F∑x = 8,66 – 20 + 10,6 = — 0,735 кН
Знак говорит о том, что равнодействующая направлен влево.
2.
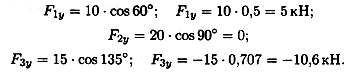 |
Определяем проекции всех сил на ось Оу значения проекций, получим величину проекции Оу.
Сложив алгебраически значения проекций, получим величину проекции равнодействующей на ось Оу.
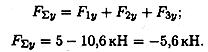 |
Знак проекции соответствует направлению вниз. Следовательно, равнодействующая направлена влево и вниз (рис. 3.7б).
3. Определяем модуль равнодействующей по величинам проекций:
 |
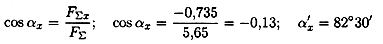 |
4. Определяем значение угла равнодействующей с осью Ох:
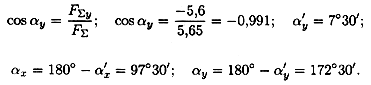 |
и значение угла с осью Оу:
Пример 3. Система трех сил находится в равновесии. Известны проекции двух сил системы на взаимно перпендикулярные оси Ох и )у:
Определить, чему равна и как направлена третья сила системы.
Решение
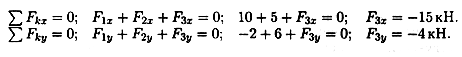 |
1. Из уравнений равновесия системы определяем:
2.
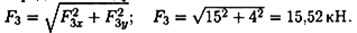 |
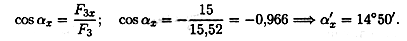 |
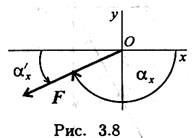
Направление вектора силы относительно оси Ох (рис. 3.8):
Угол с осью Ох будет равен
 |
Пример 4. Определить величину и направление реакций связей для схемы, приведенной на рисунке, а под действием груза G = 30 кН. Проверить правильность определения реакций.
Решение
1. В задаче рассматривается равновесие тела, опирающегося на плоскость и подвешенного на нити. Заменим тело точкой 0, совпадающей с центром тяжести.
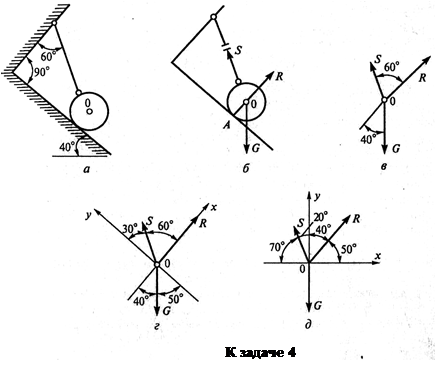
3. Мысленно отбросим связи — плоскость и нить. Заменим их действие на точку 0 реакциями связей. Реакция плоскости (обозначим ее R) проходит по нормали к плоскости в точке А, а реакция или усилие в нити (обозначим ее S) — по нити от точки. Обе реакции и вес тела или линии их действия должны пересекаться в точке 0.
Изобразим действующие силы в виде системы трех сходящихся сил на отдельном чертеже (рис. в).
4. Выберем положение системы координат. Начало координат совмещаем с точкой 0. Ось х совмещаем с направлением линии действия реакции R, а ось у направим перпендикулярно оси х (рис. г). Определим углы между осями координат и реакциями R и S. Обычно рис. б и в не выполняют отдельно, а сразу от рис. а переходят к рис. г. Можно было ось у совместить с усилием S, и ось х направить по углом 90°, тогда решение было бы другим.
5. Составим сумму проекций всех сил на оси координат:
Решим систему уравнений. Из второго уравнения находим
Из первого уравнения находим
6.Проверим решение, для чего расположим оси координат, как показано на рис. д. Составим уравнения равновесия для вновь принятых осей:
Решим систему уравнений способом подстановки.
Из первого уравнения найдем R:
Подставим это выражение во второе уравнение:
Очевидно, что при расположении осей, как показано на рис. д, вычисления оказались более сложными.
Ответ: R = 11,84 кН; S = 22,21 кН.
Пример 5. Определить усилия в нити и стержне кронштейна, показанного на рис. а, если G = 20 кН.
Решение
1. 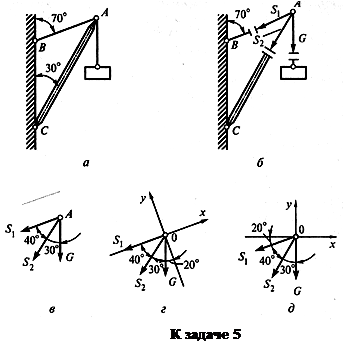
2. Активной силой является вес груза G, направленный вниз (рис. б).
3. Отбросим связи: стержень и нить. Усилие в нити обозначим Sx и направим от точки А, так как нить может испытывать только растяжение. Усилие в стержне обозначим S2 и тоже направим от точки А, предполагая что стержень АС растянут (рис. б).
Выполним на отдельном чертеже схему действия сил в точке А (рис. в).
4. Выберем положение системы координат. Начало координат совмещаем с точкой А (рис. г). Ось х совмещаем с линией действия усилия S, а ось у располагаем перпендикулярно оси х. Укажем углы между осями координат и усилиями S1.и S2.
5. Составим уравнения равновесия.
Из второго уравнения находим
Из первого уравнения находим
Знак «минус» перед S2 свидетельствует о том, что стержень АС не растянут, как предполагалось, а сжат.
6. Проверку решения предлагаем выполнить самостоятельно, расположив оси координат так, как показано на рис. д.
Ответ: S1 = 15,56 кН, S2 = — 29,24 кН (при принятом на чертеже направлении усилий).
Величина усилий зависит от углов наклона стержня и нити. Например, если на рис. а угол 70° заменить на 60°, сохранив угол 30°, то усилия будут равны: S1= 20 кН, S2 = — 34,64 кН. А при угле 50° S1 = 29,26 кН, S2 = — 44,8 кН. Оба усилия растут и становятся больше веса груза.
Пример 6. Как изменятся усилия в стержне и нити, если груз будет перекинут через блок, как показано на рис. а?
Остальные данные — в примере 5.
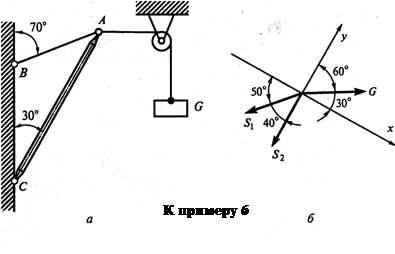
1. Рассматриваемой тонкой остается точка А.
2. Активная сила (вес груза G) действует на точку горизонтально слева направо, так как груз перекинут через блок.
3. Усилия S1 и S2 прикладываем к точке А, как в примере 2.
4. Выбираем систему координат, как показано на рис. б.
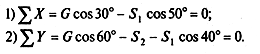 |
5. Составляем и решаем уравнения равновесия:
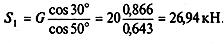 |
Из первого уравнения находим
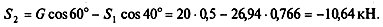 |
Из второго уравнения находим
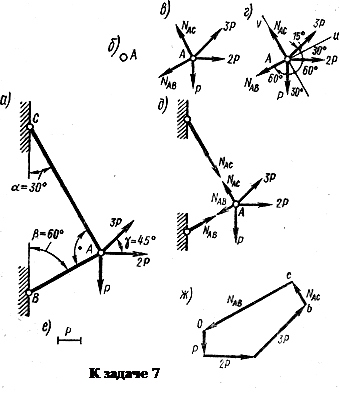
Пример 7. Определить усилия в стержнях (рис. а). Массой стержней пренебречь.
Решение
В соответствии с последовательностью действий, будем рассматривать равновесие узла А к которому приложены заданные нагрузки (Р, 2Р, 3Р) и искомые реакции стержней АВ и АС.
Освободим узел А от связей, заменим их действие искомыми реакциями NАС, NAB(рис. в). Получили плоскую систему сходящихся сил.
Выбираем систему координат (рис. г).
Сила NAB перпендикулярна оси v, сила NАС — оси и; поэтому в каждое уравнение равновесия войдет лишь одна неизвестная сила:
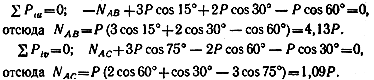 |
Силы NAB и NАС получились положительными; это значит, что предполагаемые направления сил совпадают с действительными.
На рис. д показаны силы, действующие на узел (реакции стержней), и силы, действующие на стержни (усилия в стержнях или реакции узла).
Решим тот же пример графическим методом.
Полученная система сил (см. рис. в) находится в равновесии, и, следовательно, силовой многоугольник, построенный для этой системы сил, должен быть замкнутым.
Строим силовой многоугольник. Выбираем масштаб (рис. е). От точки О (рис. ж) в выбранном масштабе откладываем сначала силу Р, затем от конца вектора Р — силу 2Р, после чего от конца вектора 2Р — силу ЗР. Масштаб следует выбрать достаточно крупный, с тем чтобы при измерении отрезков (векторов), изображающих искомые силы, можно было получить их значения без большой погрешности. Через точку b проводим линию, параллельную стержню АС, и через точку О — линию, параллельную стержню АВ. Отрезки ОС и CB представляют собой искомые усилия. Направления заданных сил известны; стрелки, изображающие направления искомых сил, ставим таким образом, чтобы в векторном многоугольнике было единое направление обхода — в данном случае против часовой стрелки. Измерив отрезки к и Ос в соответствии с выбранным масштабом, находим абсолютные величины реакций; NAcza,2P Nab
Решение примера выполнено двумя способами, которые (в пределах точности построений) дали совпадающие результаты. Очевидно, здесь никакой дополнительной проверки решения не требуется.
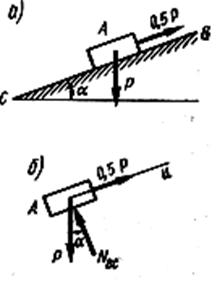
Решение
Силы, действующие на груз А, представляют собой плоскую систему сходящихся сил. NBC — реакция наклонной плоскости.
Если груз А находится в покое, то ∑Pto = 0, т.е.
Контрольные вопросы и задания
1. Запишите выражение для расчета проекции силы F на ось Оу (рис. 3.9).
2. Определите сумму проекций сил системы на ось Ох (рис. 3.10).
4. Определите величину силы по известным проекциям:
5.
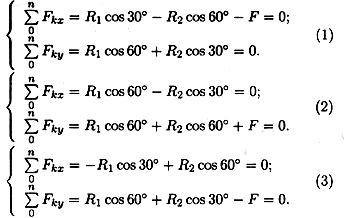 |
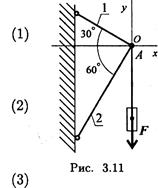
Указания.
1. При ответе на вопросы 1 и 2 необходимо знать, что в выражение для величины проекции силы на ось подставляется угол между вектором силы и положительной полуосью координат. Не забыть, что определяется алгебраическая сумма.
2. При ответе на вопрос 4 сначала следует определить возможные направления реакций в стержнях, мысленно убирая по очереди стержни и рассматривая возможные перемещения (см. лекцию 1).
Затем записать алгебраические суммы проекций сил на оси Ох и Оу. Полученные уравнения сравнить с приведенными.
📹 Видео
Система сходящихся сил. Решение задач по МещерскомуСкачать

Термех. Статика. Расчётно-графическая работа по статике №2. Задание 1 и решениеСкачать

Статика. Момент сил. Условия равновесия тел | Физика ЕГЭ, ЦТ, ЦЭ | Физика для школьниковСкачать

Статика. Условия равновесия плоской системы сил (23)Скачать

Определение реакций опор простой рамыСкачать

Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Урок 76. Задачи на правило моментовСкачать

Задача о составной конструкцииСкачать

Урок 80 (осн). Момент силы. Правило моментовСкачать

Система сходящихся силСкачать
Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1Скачать

Физика 10 класс (Урок№14 - Статика. Равновесие абсолютно твердых тел.)Скачать

Решение задачи на равновесие одного телаСкачать

Видеоурок 1. Определение реакций жёстких стержней.Скачать

Произвольная плоская система сил. Задача 1Скачать