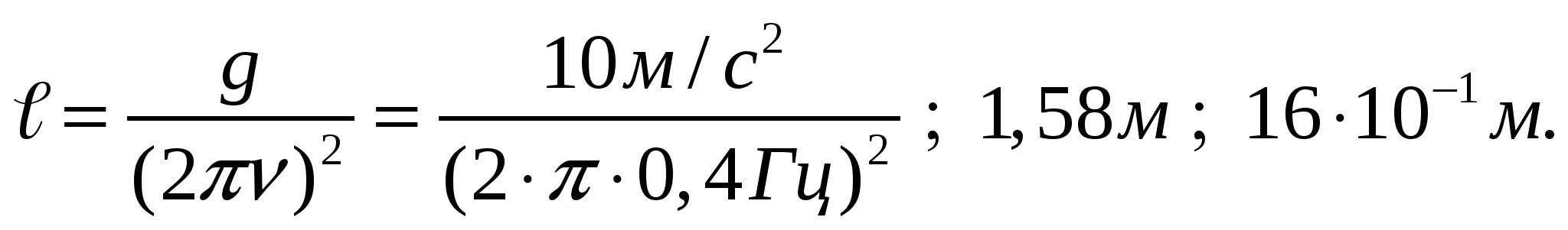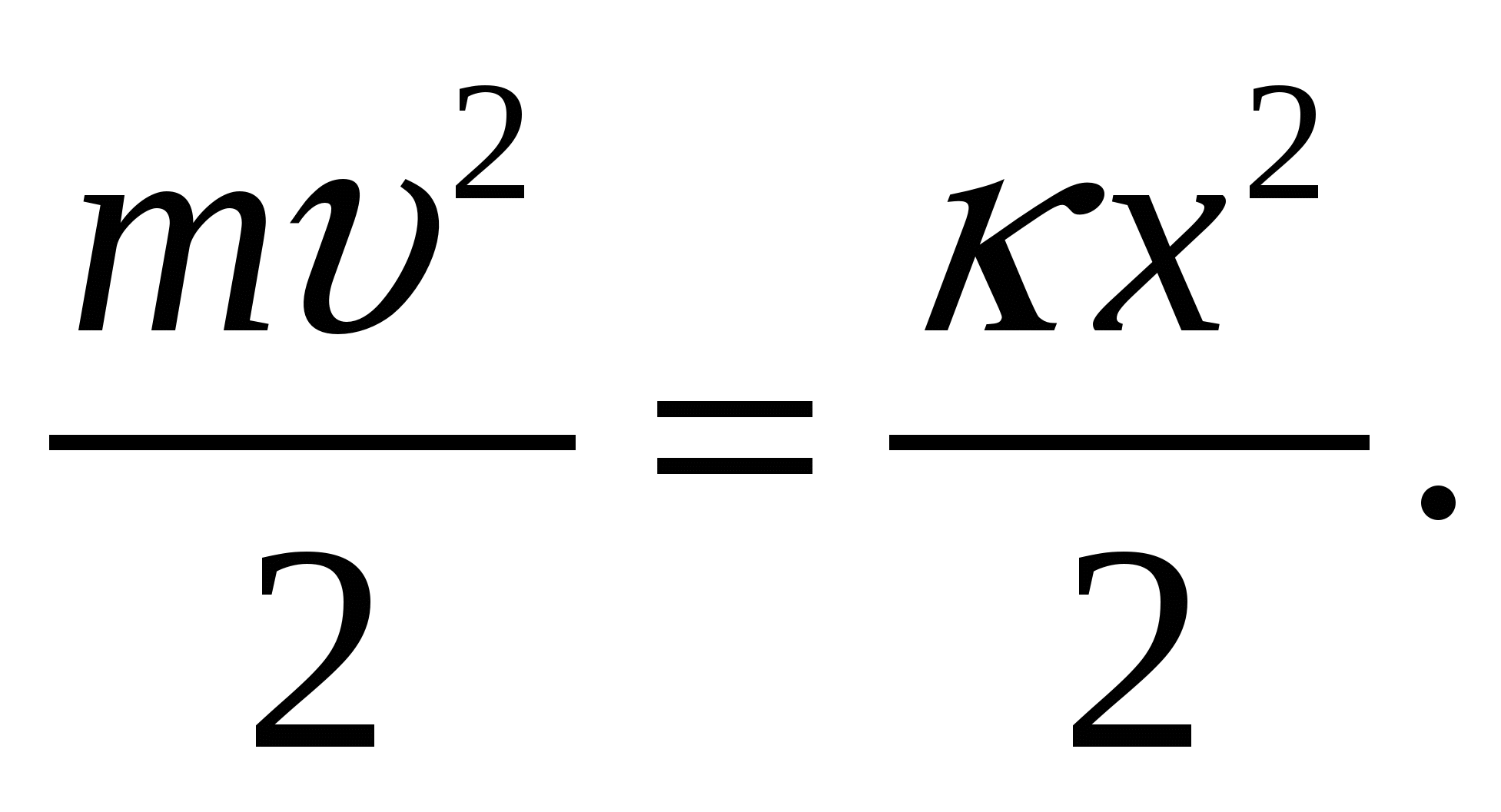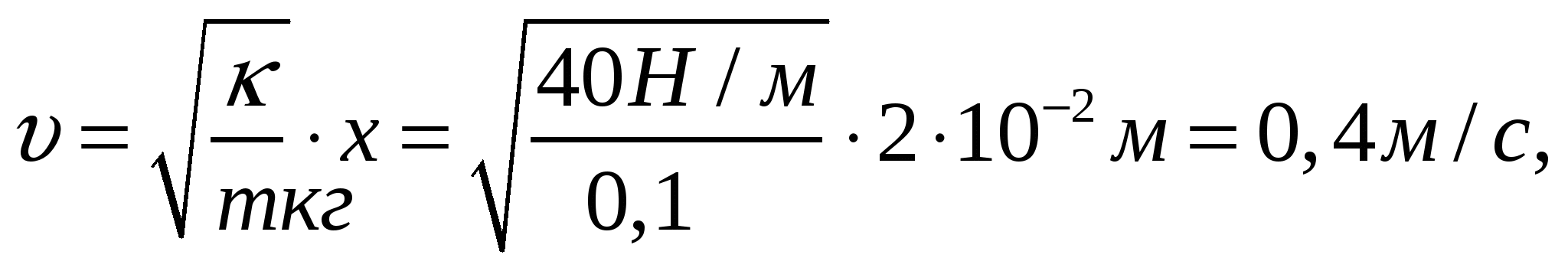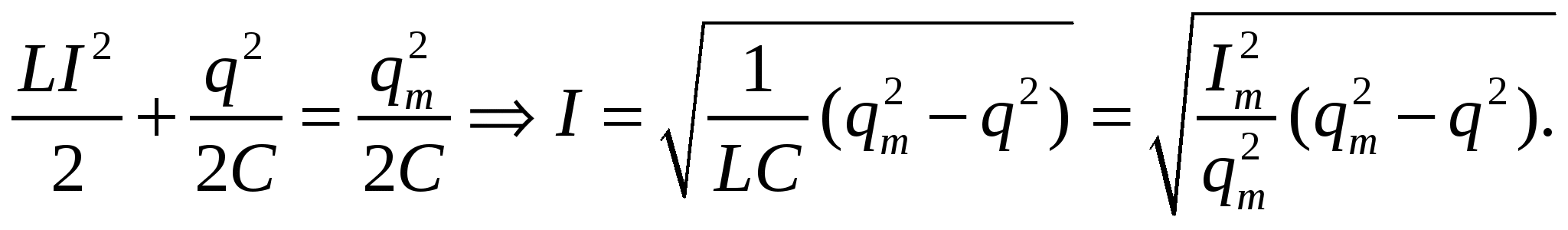Груз массой 0 1 кг колеблется так что его ускорение изменяется в соответствии с уравнением

Скорость тела, совершающего гармонические колебания меняется с течением времени в соответствии с уравнением где все величины выражены в СИ. Какова амплитуда колебаний скорости? (Ответ дайте в метрах в секунду.)

Общий вид закона изменения скорости тела со временем, совершающего колебания, имеет вид

где — амплитуда колебаний скорости. Сравнивая с заключаем, что амплитуда колебаний скорости равна

А разве закон не имеет вид:

В частном случае, да (если положить ).

.

Я совсем запутался.

В одних справочниках закон изменения скорости гармонических колебаний выглядит так:

А у вас на сайте увидел совсем другую формулу без «w» после амплитуды.

Как пользоваться такими формулами? Как тогда выглядят законы для координаты и ускорения?

Мой преподаватель говорил, что можна использовать и 1), и 2).

Все довольно просто. Сейчас я, возможно, скажу несколько сложных слов, но затем постараюсь разъяснить их смысл. Для простоты изложения речь будет идти об одномерном случае, на случай многих степеней свободы все легко обобщается.

Итак, главная задача механики — найти зависимость координаты тела от времени, то есть, по сути, найти некоторую функцию, которая каждому моменту времени сопоставляет некоторое значение координаты. Любое движение мы описываем при помощи второго закона Ньютона. В этот закон входит ускорение, которое является второй производной координаты тела по времени, и сила, которая обычно зависит от самой координаты. Также сила может зависеть от скорости тела, то есть от первой производной координаты по времени. Таким образом, с математической точки зрения второй закон Ньютона представляет некоторое соотношение между координатой, ее первой и второй производными. Такое соотношение называется в математике дифференциальным уравнение. Старшая производная, входящая в такое уравнение, — вторая. Математика говорит, что решение такого уравнения, то есть общий вид функции, удовлетворяющей нашему соотношению, зависит от двух произвольных постоянных, которые невозможно определить из уравнения. Эти произвольные постоянные определяются для каждого конкретного случая, например, при помощи так называемых начальных условий. То есть чтобы в точности понять, как будет двигаться тело, нужно знать не только, какие силы на него действуют, но и каковы его начальная координата и скорость. Две произвольные константы в решении подбираются таким образом, чтобы полученная нами функция и ее производная (то есть скорость) в начальный момент времени имели заданные значения.

Это абсолютно общая ситуация. Вспомните, когда мы говорим о движении тела с постоянным ускорением, чтобы в точности задать движение нам нужно именно два числа, начальная координата и начальная скорость.

Тоже самое справедливо и для колебания. Колебание конкретного маятника (то есть маятника с заданной собственной частотой) определяется также двумя числами. Обычно решение уравнения для маятника, получаемого из второго закона Ньютона, записывают в виде .

Здесь и играют как раз роль произвольных постоянных, которые нужно определять из начальных условий. Посчитаем скорость: . Пусть нам известно, что в нулевой момент времени координата и скорость маятника были равны и . Решив систему обычных уравнений , можно найти конкретные выражения для и через и .

Не буду приводить ответ в общем случае, если Вы захотите, то легко сделаете это сами. Расскажу только о конкретных случая. Пусть, например, известно, что в нулевой момент времени тело находится в положении равновесия (то есть ), а его скорость равна своей максимальной величине (то есть ). Тогда получаем для нашего конкретного случая, что система уравнений приобретает вид: . Из первого уравнения сразу понятно, что (первому уравнению, конечно, удовлетворяет и условие , но тогда наше решение получится нулевым, а нас это не устраивает). Второе тогда приобретает вид: , откуда . Таким образом мы нашли выражения для обеих постоянных. В итоге имеем: . При этом для ускорения получается . Если теперь обозначить через более привычное выражение для амплитуды , получатся более привычные формулы.

Рассмотрим еще один пример. Пусть теперь груз находится в крайнем положении, то есть его скорость равна нулю. Будем считать, что от отклонился в отрицательную сторону оси, то есть его координата равна . Тогда уравнения на начальные условия приобретают вид: . Из второго уравнения . Из первого: . Таким образом, для координаты имеет: (второе равенство при помощи формулы приведения). Для скорости: . Для ускорения: .

Конкретные формулы зависят от начальных данных. С учетом периодичности синусов и косинусов, пользуясь разными формулами приведения, можно из формул убирать знаки добавлять фазы и т.д.

Что касается формулы в задаче, там нет , частоты, так как подставлено ее конкретное значение:

Видео:ТИПОВЫЕ ЗАДАЧИ ПО ХИМИИ: Химическое Количество Вещества, Моль, Молярная Масса и Молярный ОбъемСкачать

Контрольная работа по физике 11 класс за 1 полугодие

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

311 лекций для учителей,
воспитателей и психологов

Получите свидетельство
о просмотре прямо сейчас!

Контрольная работа по физике 11 класс за первое полугодие

( Учебник Г.Я.Мякишев и

Цель работы: контроль усвоения программы курса физики за 1 полугодие, на что необходимо обратить внимание при подготовке к ЕГЭ по этим темам

Время проведения – 60 минут

Зависимость некоторых величин от времени имеют следующий вид:

; ; ; .

Какая из этих величин совершает гармоническое колебание?

1) 2)

3) 4)

На рисунке представлена зависимость координаты центра шара, подвешенного

на пружине, от времени. Амплитуда колебаний равна

Если длину математического маятника уменьшить в 4 раза, то период его колебаний

1) увеличится в 2 раза

2) уменьшится в 2 раза

3) увеличится в 4 раза

4) уменьшится в 4 раза

К пружине жесткостью 40 Н/м подвешен груз массой 0,1 кг. Период свободных колебаний этого пружинного маятника равен:

Амплитуда малых свободных колебаний пружинного маятника 4 см, массагруза400 г, жесткость пружины 40 Н/м. Максимальная скорость

колеблющегося груза равна

1) 0,4 м/с 2) 0,8 м/с

На рисунке представлен график зависимости потенциальной энергии математического маятника (относи-тельно положения его равновесия) от времени. В момент времени =1с полная механическая энергия маятника равна

1) 0 Дж 2) 10Дж 3) 20

Сила тока через резистор меняется по закону . Действующее значение силы тока в цепи равно

А8. Точка совершает колебания по закону x=A cosωt, где A=5 см; ω=2 радс .

Определить максимальное ускорение , период Т.

1. а=20м/с 2. а=0,2м/с 3. а=2м/с

Т=П рад/с Т=П рад/с Т=2П рад/с

А9 На рисунке приведен график зависимости силы тока от времени в колебательном контуре с катушкой, индуктивность которой равна 0,2 Гн. Максимальное значение энергии электрического поля конденсатора равно

Тело массой 0,1 кг колеблется так, что проекция ускорения его движения зависит от времени в соответствии с уравнением . Чему равна проекция силы на ось ОХ, действующая на тело в момент времени ? Умножьте ответ на 10.

На рисунке представлен график зависимости силы тока от времени в колебательном контуре.

На каком из графиков правильно показан процесс изменения заряда на конденсаторе?

Индуктивность катушки равна 0,125 Гн. Уравнение колебаний силы тока в ней имеет вид: , где все величины выражены в СИ. Определите амплитуду напряжения на катушке

В уравнении гармонического колебания величина, стоящая под знаком косинуса, называется:

2) начальной фазой

3) смещением от положения равновесия

4) циклической частотой

На рисунке представлена зависимость координаты центра шара, подвешенного на пружине, от времени. Период колебаний равен

Как изменится период свободных гармонических колебаний математического маятника, если массу груза увеличить в 3 раза?

1) увеличится в 9 раз

2) уменьшится в 3 раза

3) уменьшится в 9 раз

Если груз, подвешенный на пружине жесткостью 250 Н/м, совершает свободные колебания с циклической частотой 50 рад/с, то масса равна

С какой скоростью проходит груз пружинного маятника, имеющего массу 0,1 кг, положение равновесия, если жесткость пружины 40 Н/м, а амплитуда колебаний 2 см?

1) 0,1 м/с 2) 0,4 м/с

Напряжение на выходных клеммах генератора меняется по закону . Действующее значение напряжения в этом случае равно

1) 396 В 2) 280 В

На рисунке представлен график зависимости потенциальной энергии математического маятника (относи-тельно положения его равновесия) от времени. В момент времени = 2с полная механическая энергия маятника равна

Заряд конденсатора идеального колебательного контура, состоящего из катушки с индуктивностью 25 мкГн и конденсатора, при свободных колебаниях меняется по закону , где все величины выражены в СИ. Максимальная энергия конденсатора равна

3) 100 мДж 4) 0,5 мкДж

На рисунке представлен график изменения со временем кинетической энергии ребенка, качающегося на качелях. В момент, соответствующий точке А на графике, его полная механическая энергия равна

Груз массой , подвешенный к пружине, совершает колебания с периодом и амплитудой . Что произойдет с периодом, максимальной потенциальной энергией пружины и частотой, если при неизменной амплитуде уменьшить массу?

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

В) Максимальная потенциальная энергия пружины

Получившуюся последовательность цифр перенесите в бланк ответов (без пробелов и каких-либо символов)

В2На рисунке представлен график зависимости силы тока от времени в колебательном контуре.

На каком из графиков правильно показан процесс изменения энергии магнитного поля катушки?

Индуктивность катушки равна 0,5 Гн. Уравнение колебаний силы тока в ней имеет вид: , где все величины выражены в СИ. Определите амплитуду напряжения на катушке

На выполнение контрольной работы учащимся отводится 60мин. За задание А -1балл, за задание Б-2балла.

Максимальное количества баллов 15.

вариант 1 вариант 2

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Педагогические основы деятельности учителя общеобразовательного учреждения в условиях ФГОС

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

• Сейчас обучается 49 человек из 21 региона

Курс повышения квалификации

Профессиональные компетенции педагога в рамках Федерального закона «Об образовании в Российской Федерации» №273-ФЗ от 29.12.2012

«Домашнее обучение. Лайфхаки для родителей»

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Видео:Груз массой 1 кг равномерно втаскивают по шероховатой плоскости, имеющей высоту 0,6 м и - №26073Скачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 856 248 материалов в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 30.12.2015
• 2999
• 7

• 30.12.2015
• 418
• 1

• 30.12.2015
• 368
• 1

• 30.12.2015
• 414
• 1

• 30.12.2015
• 524
• 1

• 30.12.2015
• 815
• 0

• 30.12.2015
• 996
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 30.12.2015 32379
• DOCX 213.2 кбайт
• 354 скачивания
• Рейтинг: 3 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Камышева Ольга Витальевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 7 месяцев
• Подписчики: 0
• Всего просмотров: 57618
• Всего материалов: 22

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

«Учёт особенностей развития семьи обучающегося при взаимодействии родителей и педагогов»

«Особенности развития и организации внимания ребенка»

«Творческая работа с детьми (3-10 лет) по теме Подарок маме (цветы)»

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Онлайн-тренинг «Как закрыть гештальт: практики и упражнения»

Время чтения: 3 минуты

Тысячи учителей в Австралии вышли на забастовку

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Урок 87. Движение по наклонной плоскости (ч.1)Скачать

Программа элективного курса по физике «Технология решения задач» 11 класс

Решение задач по теме «Колебания»

Bl (2002) Вариант 1

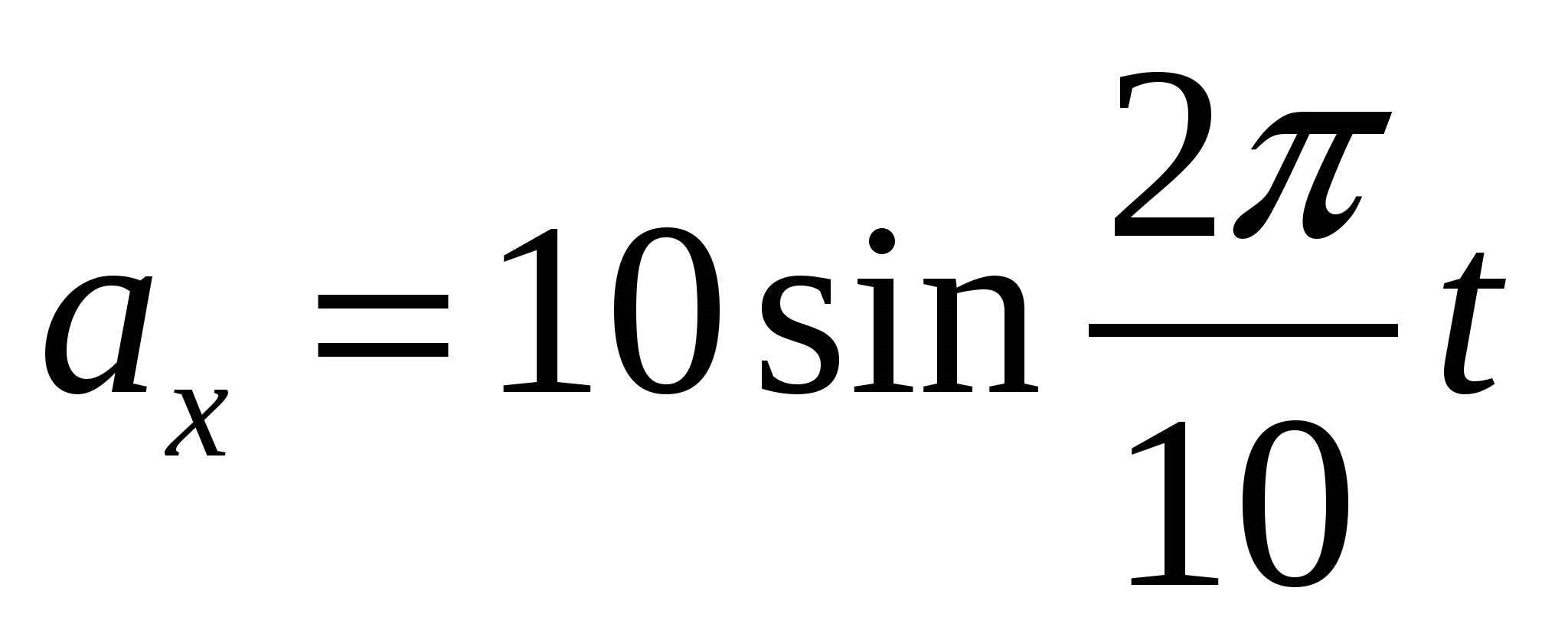
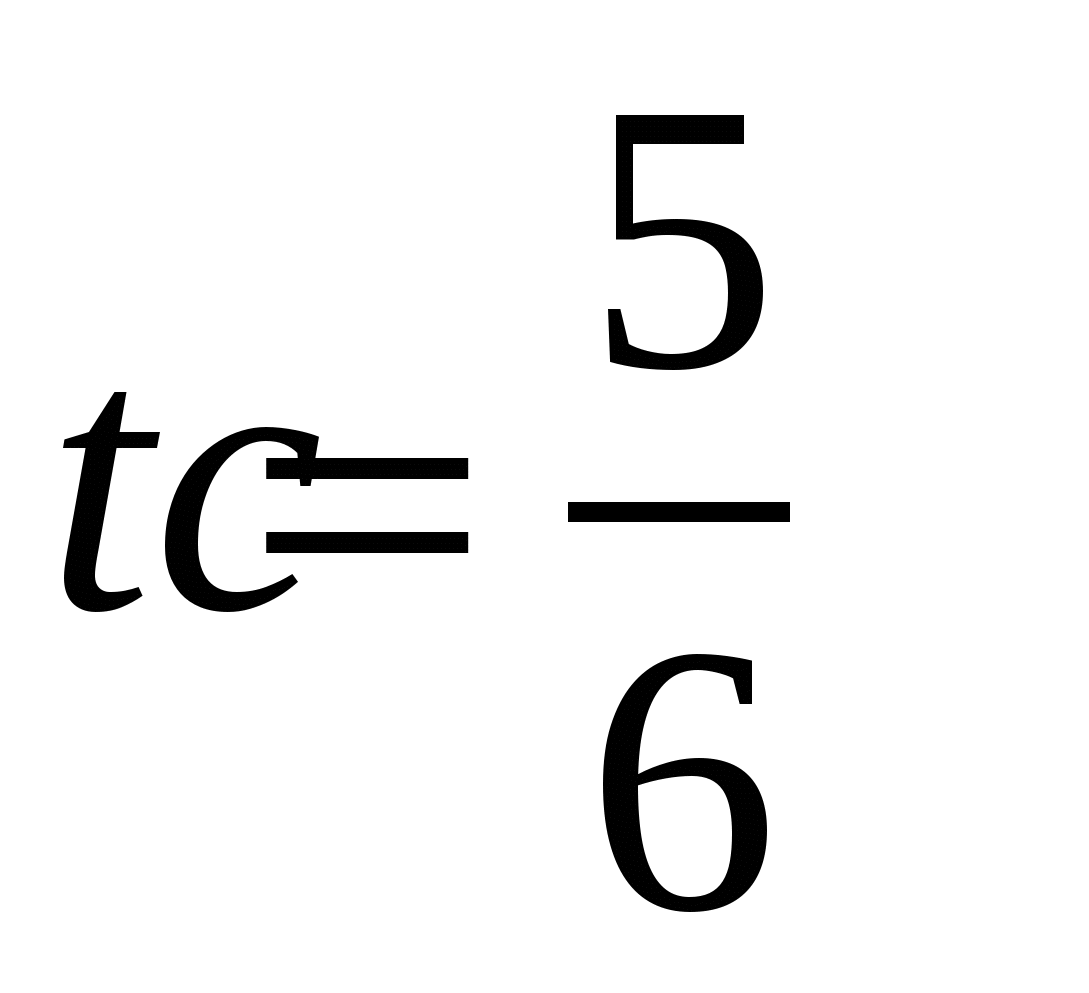
Тело массой 0,1 кг колеблется так, что проекция а _х ускорения его движения зависит от времени в соответствии с уравнением . Чему рав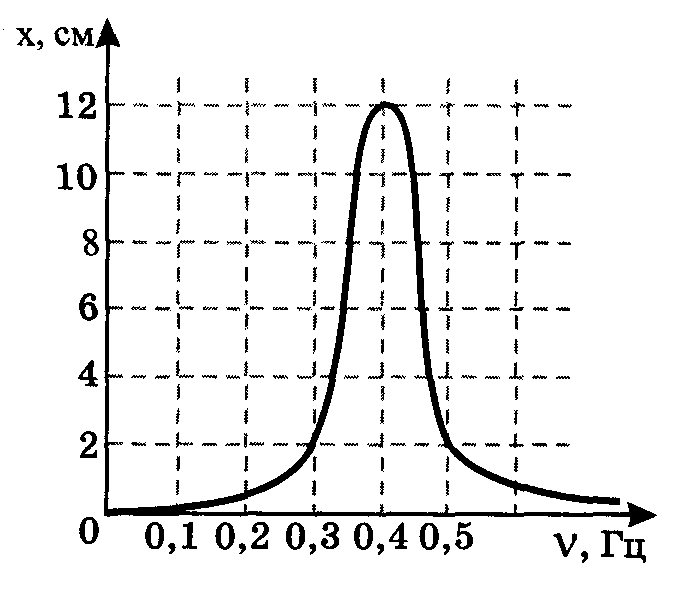на проекция силы на ось ОХ, действующей на те­ло в момент времени ? Умножьте ответ на 10 и полученное число запишите в бланк. Ответ: 5

В1 (2002) Вариант 5

На рисунке приведен график зависимости амплитуды колебаний маятника (груза на нити) от частоты изменения внешней силы. Чему равна длина маятника? Полученный ответ в метрах округлите до двух значащих цифр и умножьте на 10.

Решение: Резонансная частота- это частота вынуждающей силы, при которой амплитуда колебаний маятника максимальна. Из рисунка к задаче видно, что частота равна ν ₀=0,4 Гц. Частота вынуждающей силы становится резонансной тогда, когда совпадает с собственной частотой колебания системы.

В данном случае система представляет собой математический маятник, поэтому, частоту его колебаний можно найти по формуле ,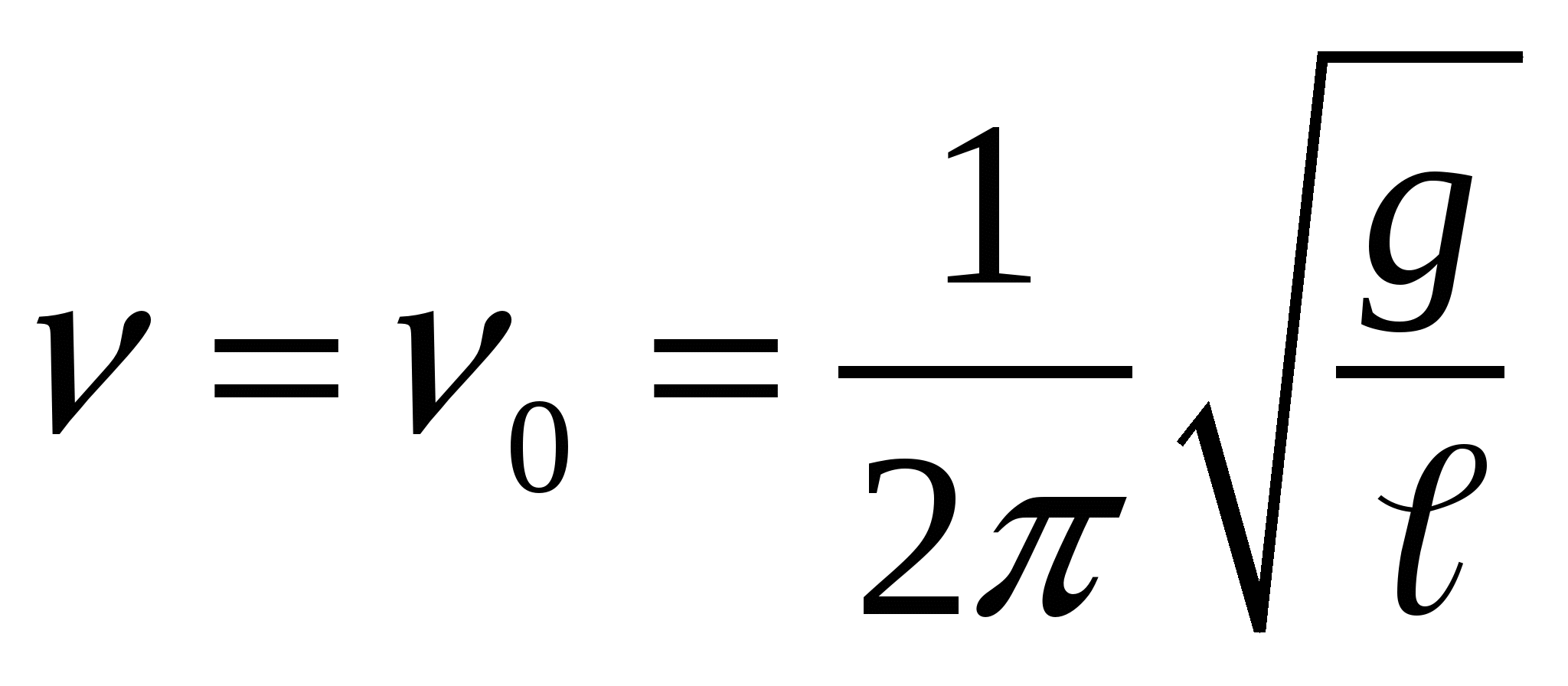

где g -ускорение свободного падения, а 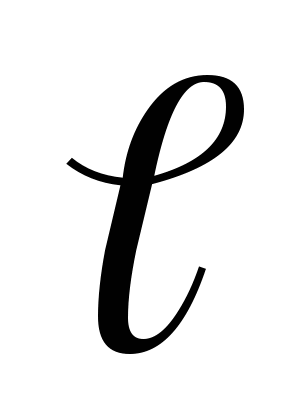— длина маятника.

А6 (2003) Вариант 1.

Амплитуда свободных колебаний тела равна 0,5 м. Какой путь прошло это тело за время, равное 5 периодам колебаний?

1) 10м. 2) 2,5 м. 3) 0,5м. 4) 2м.

Решение: Если амплитуда свободных колебаний равна 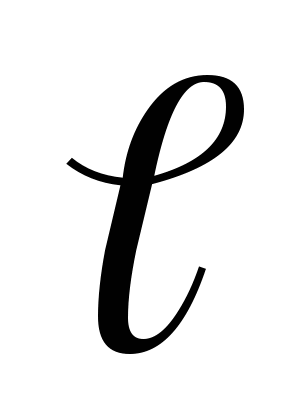, то путь, пройденный телом за один период, равен S ₁=4, а за пять периодов: S ₅=20=20·0,5 м=10м.

А6 (2003) Вариант 2.

Амплитуда колебаний пружинного маятника равна 2 см. Жесткость пружины маятника 40 Н/м, масса груза 0,1 кг. С какой скоростью груз проходит положение равновесия?

1) 0,2 м/ c . 2) 0,4 м/с. 3) 4 м/с. 4) 5м/с

Решение: По закону сохранения энергии

Отсюда

где m — масса тела, 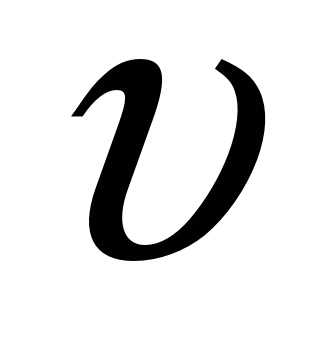— скорость тела, когда оно проходит положение равновесия, к— жесткость пружины, а х— амплитуда колебания тела.

А6 (2003) Вариант 5.

Тело, подвешенное на пружине, совершает гармонические колебания с частотой ν . Потенциальная энергия упругой деформации пружины:

изменяется с частотой .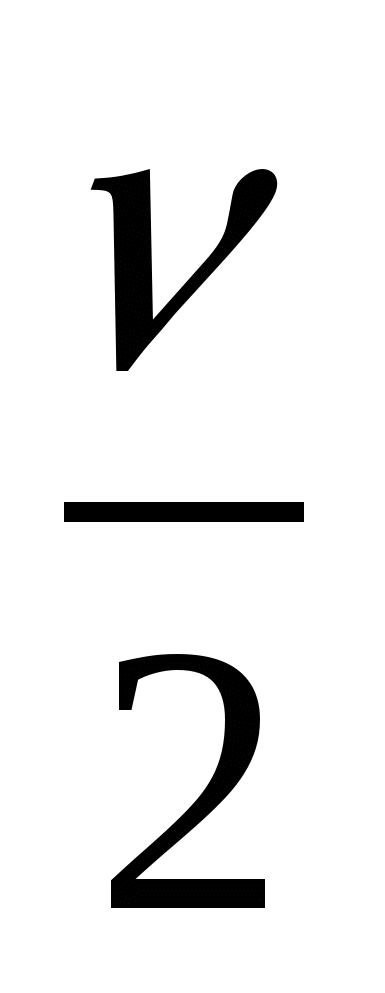

изменяется с частотой .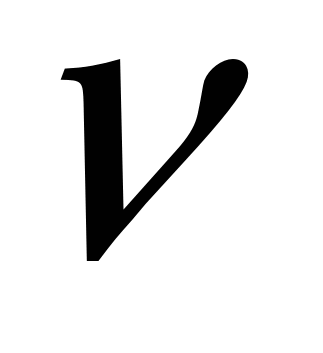

изменяется с частотой .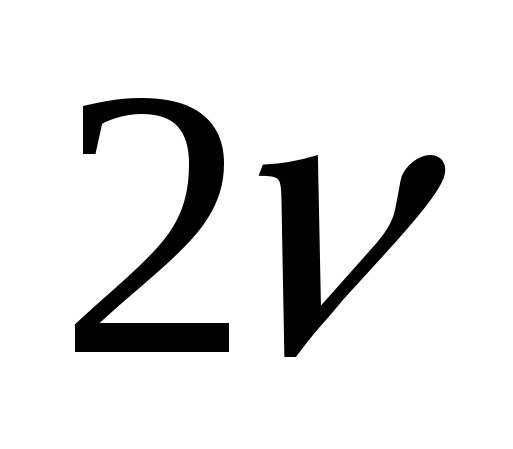

Решение: Колебания пружинного маятника являются гармоническими, следовательно, уравнение движения можно записать в виде:

, где х( t )- изменение координаты от времени, х₀— амплитуда колебания.— угловая частота колебания, t — время, а — начальная фаза.

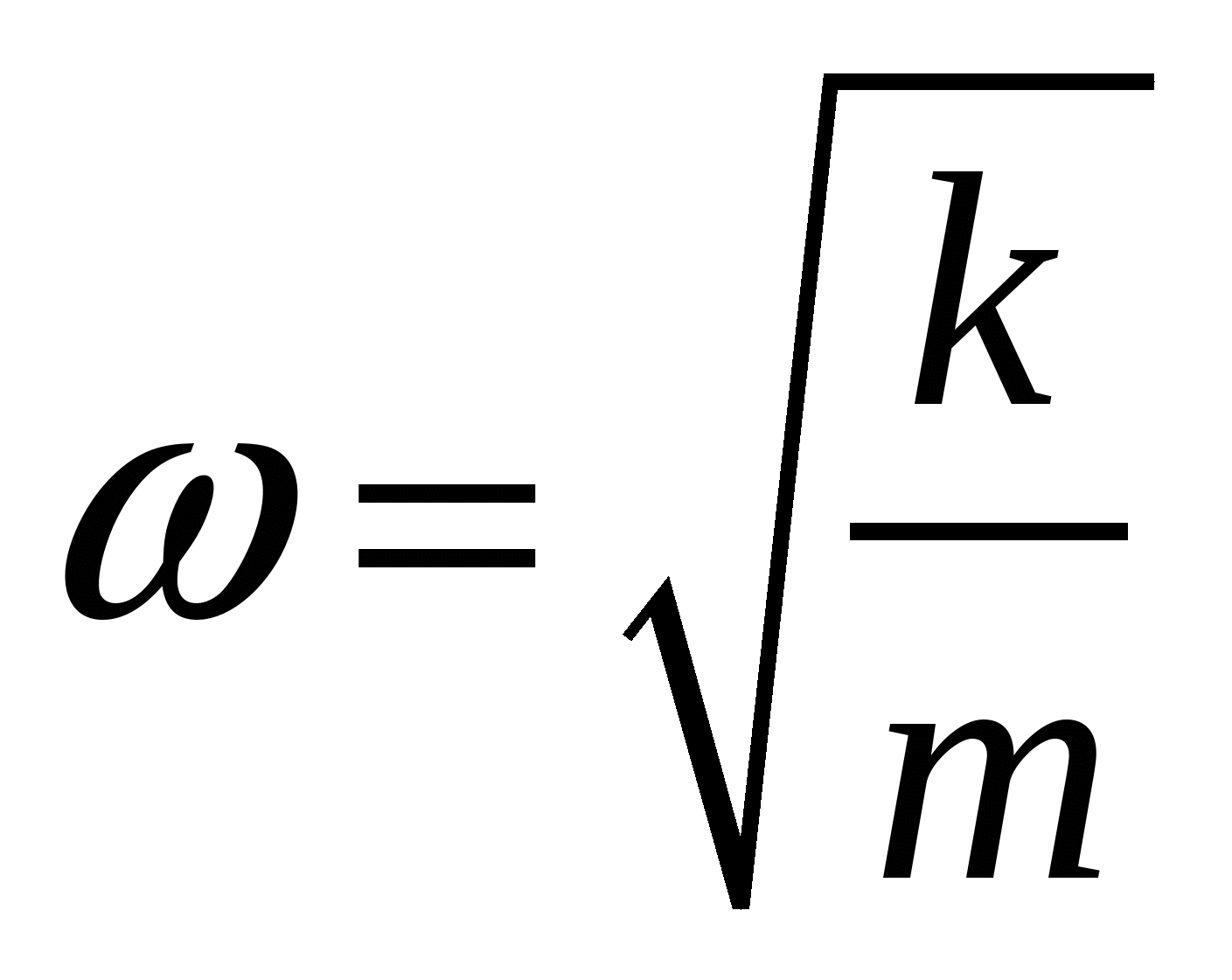
Потенциальная энергия упруго деформации пружины определяется по формуле:

, где к- жесткость пружины. Таким образом, если тело совершает гармонические колебания с частотой ν, то потенциальная энергия упругой деформации пружины изменяется с частотой 2ν.

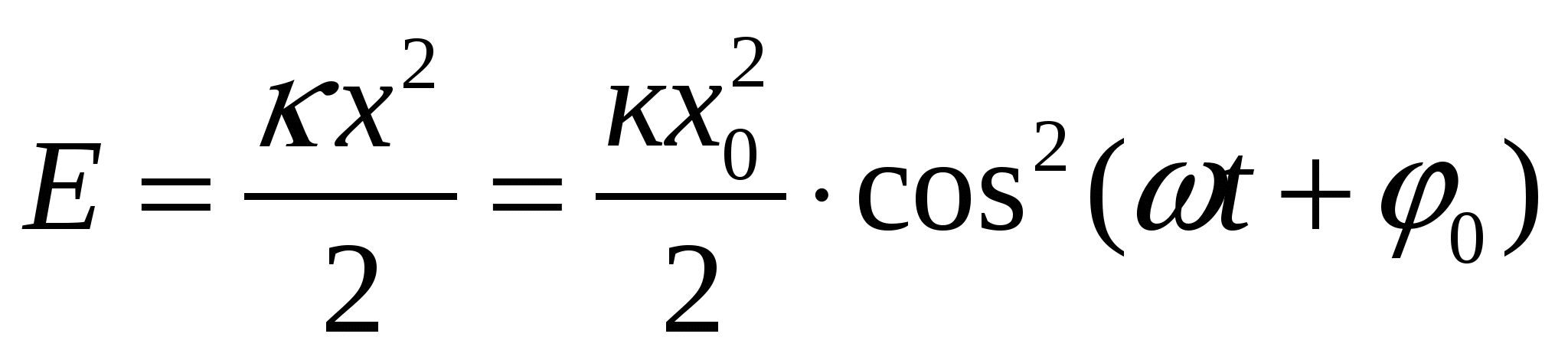
А19 (2003) Вариант 5.

К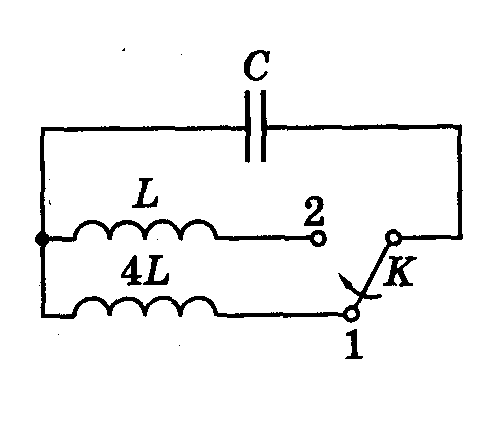ак изменится частота собственных электромагнитных колебаний в контуре (см. рис.), если ключ К перевести из положения 1 в положение 2?

Уменьшится в 2 раза.

Увеличится в 2 раза.

Уменьшится в 4 раза.

Увеличится в 4 раза.

Решение: Частота собственных колебаний колебательного контура находится по формуле

, где -угловая частота, L — индуктивность колебательного контура, а С- емкость колебательного контура.

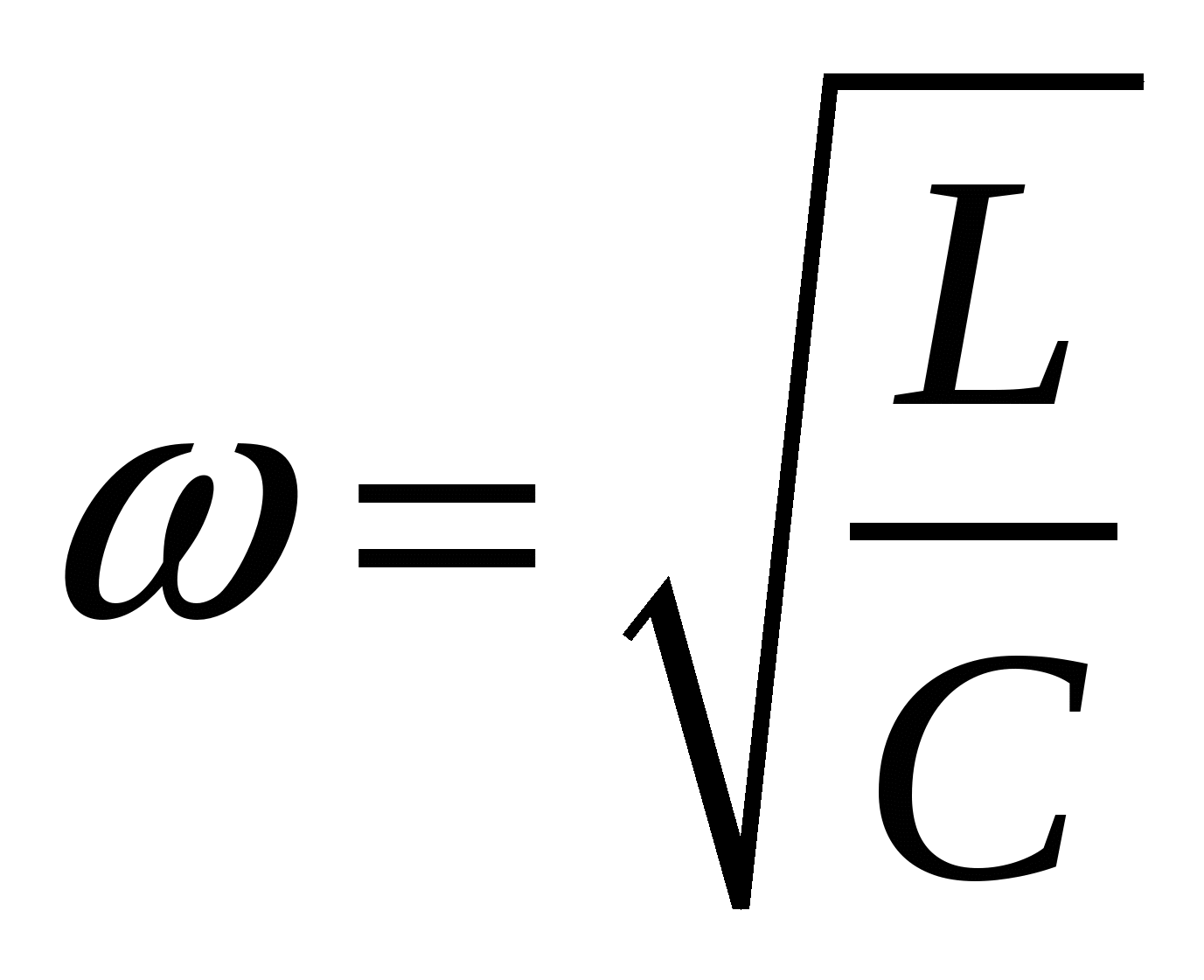
Таким образом, .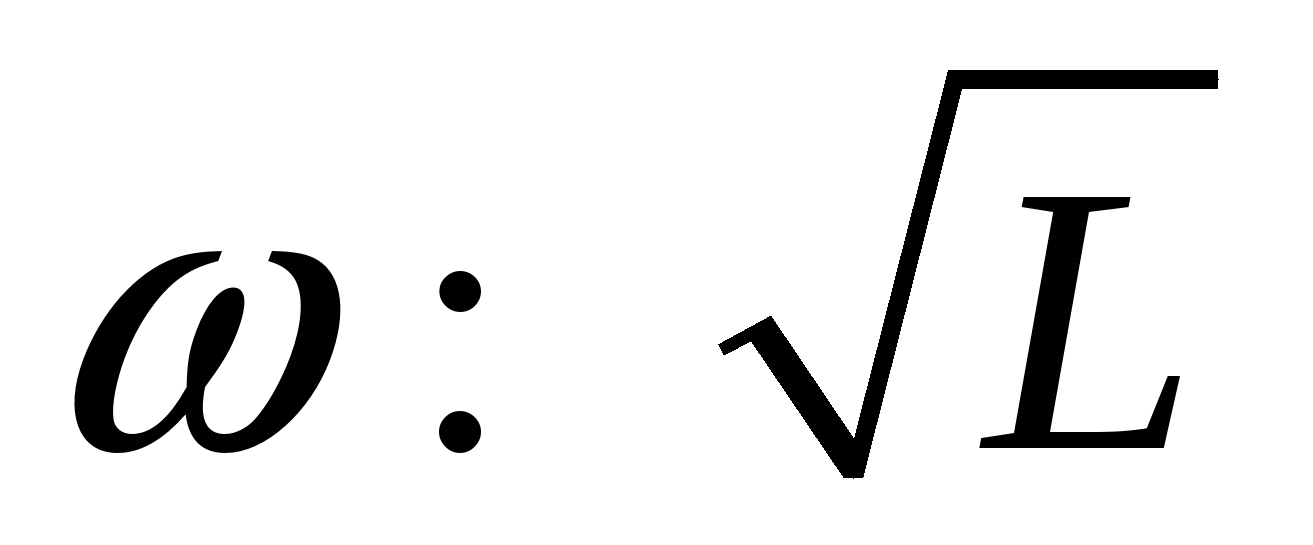

Индуктивность колебательного контура в случае, когда ключ находится в положении 1 ( рисунок к задаче), равна L , а когда ключ находится в положении 2, равна 4 L . Следовательно, при переключении ключа из положения 1 в положение 2 частота собственных колебаний увеличится в 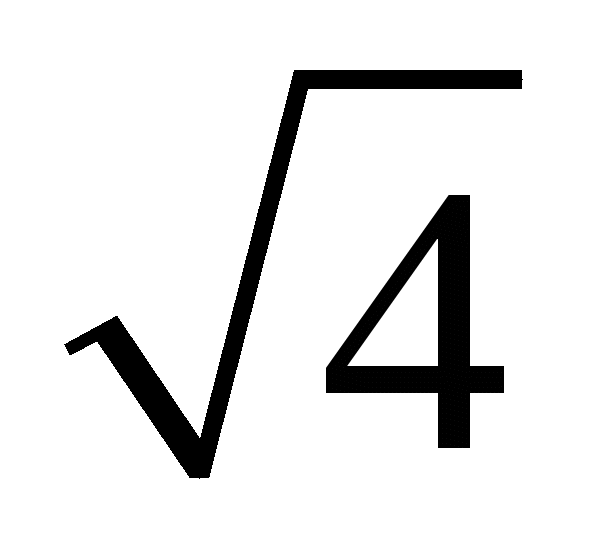=2 раза.

C 3 (2002) Вариант 1

В идеальном колебательном контуре амплитуда колебаний силы тока в катушке индуктивности равна I _m = 5 мА, а амплитуда колебаний заряда конденсатора равна q _m = 2,5 нКл. В момент времени t заряд кон­денсатора q =1,5 нКл. Найдите силу тока в катушке в этот момент.

Решение: По закону сохранения энергии:

.

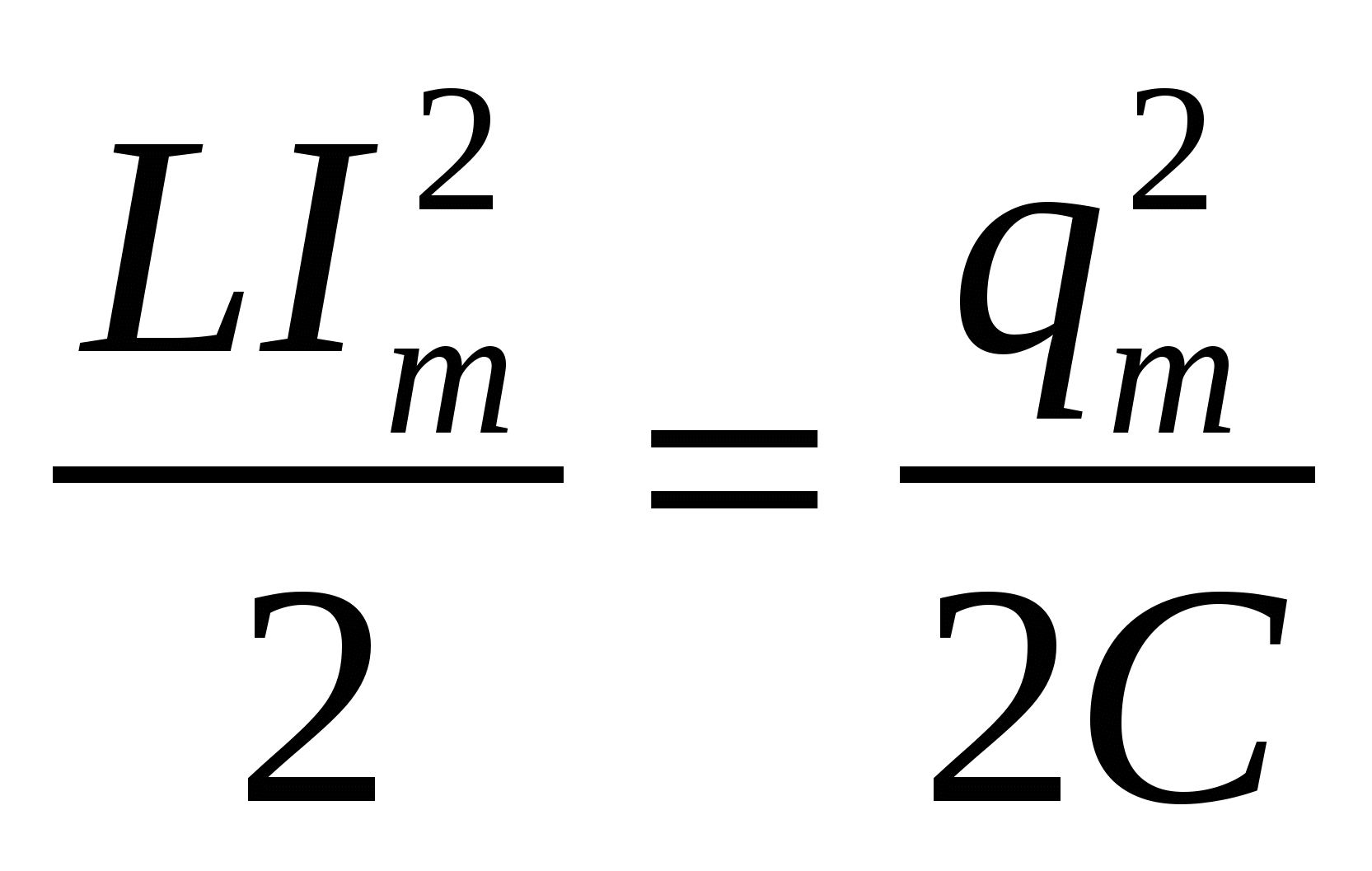
Пусть I — искомая сила тока, тогда

Следовательно, .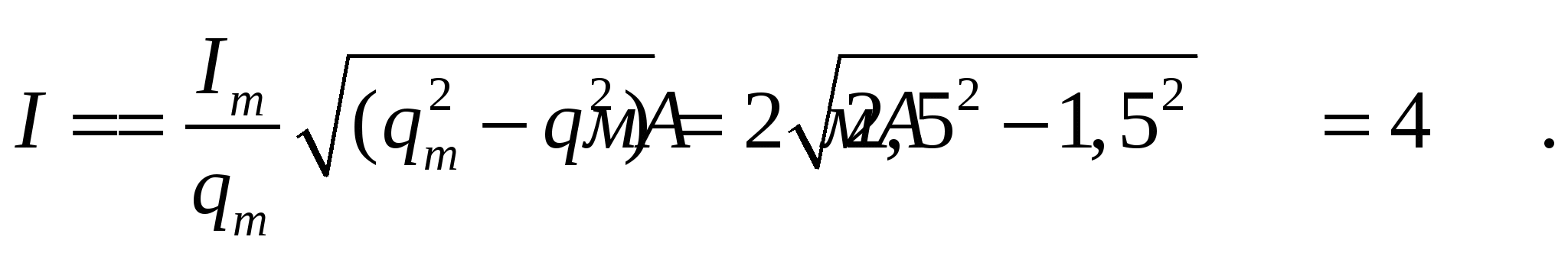

C 3 (2003) Вариант 6.

Определите период электромагнитных колебаний в колебательном контуре, если амплитуда силы тока равна I _m , а амплитуда электрического заряда на пластинах конденсатора равна q _{m .}

Решение: Запишем закон сохранения энергии в колебательном контуре

, где q _m -амплитуда электрического заряда в конденсаторе, С- емкость конденсатора, I _m -амплитуда силы тока, L — индуктивность, а Т- период колебаний.

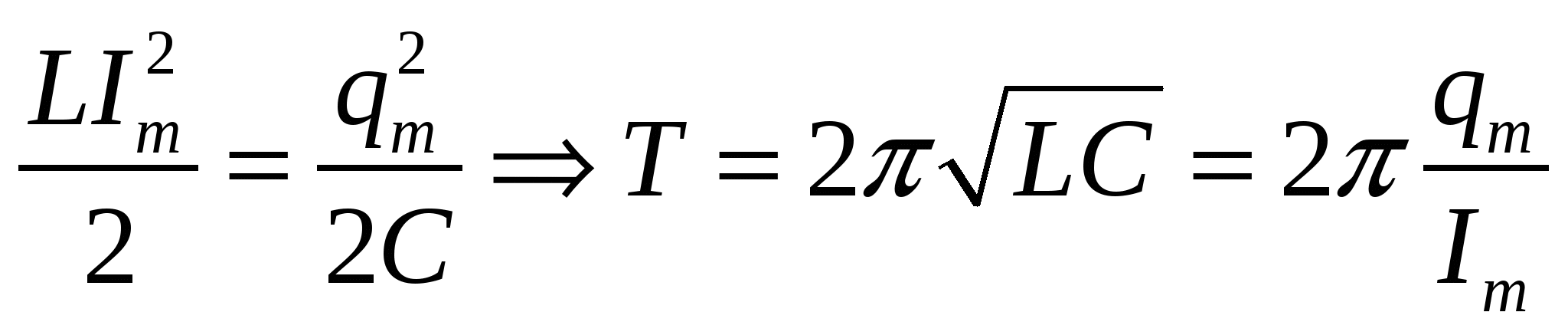
Ответ: .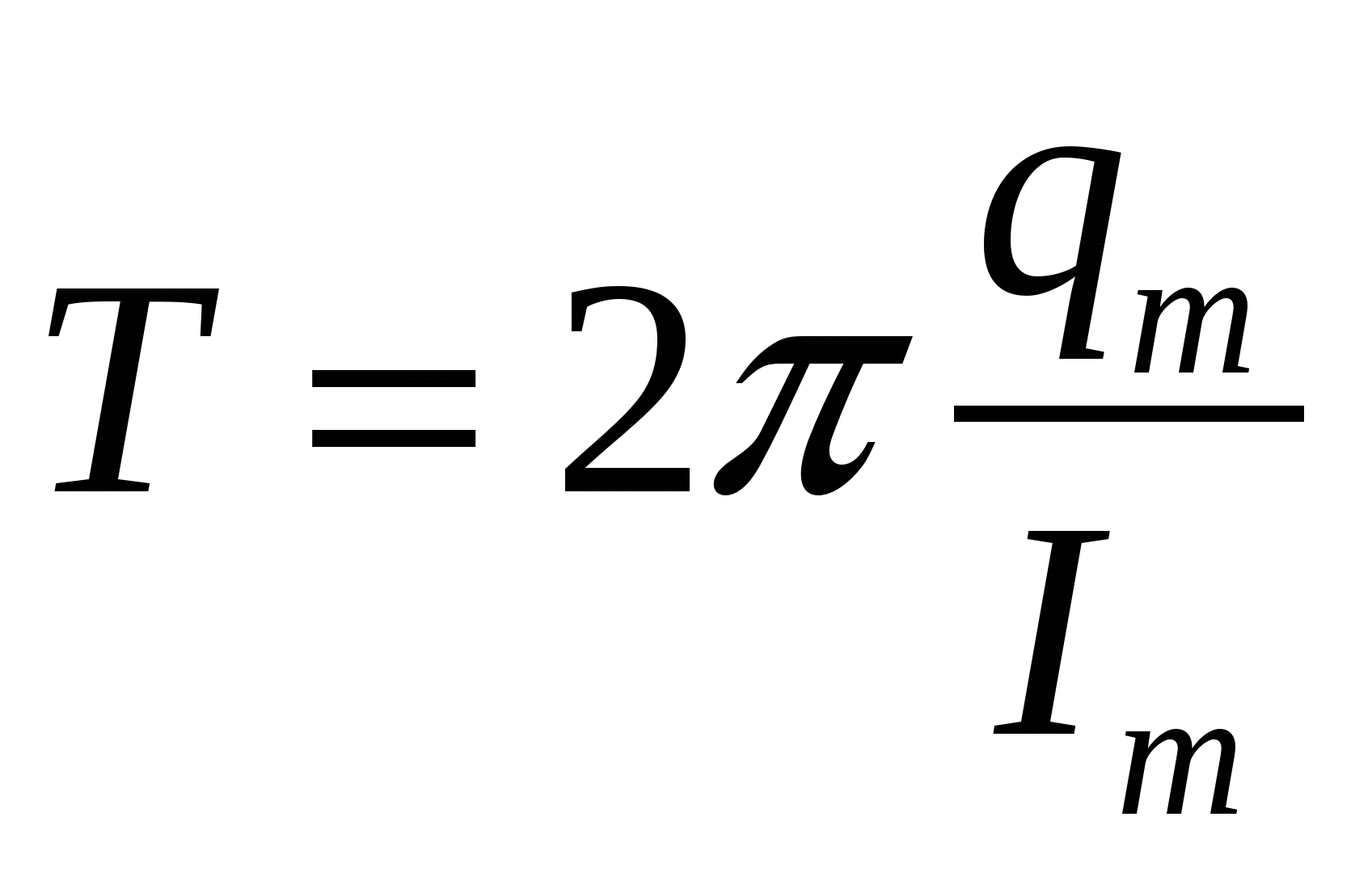

В3 (2004) Вариант 2

В таблице показано, как изменялся заряд конденсатора в колебательном контуре с течением времени.

Видео:ФИЗИКА ОГЭ 2024 ВАРИАНТ 1 КАМЗЕЕВА РАЗБОР ЗАДАНИЙ I Эмиль Исмаилов - Global_EEСкачать

Груз массой 0 1 кг колеблется так что его ускорение изменяется в соответствии с уравнением

Электронный учебник по физике 10 класса

по учебнику Мякишева Г.Я., Буховцева Б.Б., Сотского Н.Н.

С1 Тело, свободно падающее с некоторой высоты без начальной скорости, за время τ = 1 с после начала движения проходит путь в п = 5 раз меньший, чем за такой же промежуток времени в конце движения. Найдите полное время движения.

С1 Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен 30°. На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика в момент первого удара направлена вертикально вниз и равна 1 м/с. Ответ: L =0,173 м

С1 Небольшая шайба после удара скользит вверх по наклонной плоскости из точки А (см. рисунок). В точке касания В наклонная плоскость без излома переходит в наружную поверхность горизонтальной трубы радиусом R = 0,4 м. Если в точке А скорость шайбы превосходит v ₀ = 4 м/с, то в точке В шайба отрывается от опоры. Длина наклонной плоскости АВ = L =1 м, угол а = 30°. Найдите коэффициент трения μ между наклонной плоскостью и шайбой.

C 3 По прямому горизонтальному проводнику длиной 1 м с площадью поперечного сечения 1,25*10 -5 м 2 подвешенному с помощью двух одинаковых невесомых пружинок жесткостью 100 Н/м, течет ток I = 10 А (см. рисунок). Какой угол а составляют оси пружинок с вертикалью при включении вертикального магнитного поля с индукцией В= 0,1 Тл, если абсолютное удлинение каждой из пружинок при этом составляет 7*10 -3 м? (Плотность материала проводника 8*10 3 кг/м 3 ). Ответ: a =45

C 3 Положительно заряженная пылинка, имеющая массу 10 -8 г и заряд 1,8*10 -14 Кл, влетает в электрическое поле конденсатора в точке, находящейся посередине между его пластинами (см. рисунок). Минимальная скорость, с которой пылинка должна влететь в конденсатор, чтобы затем пролететь его насквозь, равна 30 м/с. Расстояние между пластинами конденсатора 1 см, напряженность электрического поля внутри конденсатора 500 кВ/м. Чему равна длина пластин конденсатора? Силой тяжести пренебречь. Система находится в вакууме. Ответ: l=0,1 м.

С4 Условимся считать изображение на пленке фотоаппарата резким, если вместо идеального изображения в виде точки на пленке получается изображение пятна диаметром не более некоторого предельного значения. Поэтому, если объектив находится на фокусном расстоянии от пленки, то резкими считаются не только бесконечно удаленные предметы, но и все предметы, находящиеся дальше некоторого расстояния d . Оцените предельный размер пятна, если при фокусном расстоянии объектива 50 мм и диаметре входного отверстия 5 мм резкими оказались все предметы, находившиеся на расстояниях более 5 м от объектива. Сделайте рисунок, поясняющий образование пятна. Ответ: =0,05м.

С4 В электрической цепи, показанной на рисунке, ЭДС источника тока равна 12 В; емкость конденсатора 2 мФ; индуктивность катушки 5 мГн, сопротивление лампы 5 Ом и сопротивление резистора 3 Ом. В начальный момент времени ключ K замкнут. Какая энергия выделится в лампе после размыкания ключа? Внутренним сопротивлением источника тока пренебречь. Сопротивлением катушки и проводов пренебречь.

💡 Видео

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Урок 34. Свободное падение. Ускорение свободного паденияСкачать

Урок 330. Скорость и ускорение при гармонических колебанияхСкачать

ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 классСкачать

Урок 329. Задачи на гармонические колебания - 1Скачать

Наклонная плоскость. Расстановка сил | 50 уроков физики (6/50)Скачать

Урок 109 (осн). Задачи на вычисление количества теплотыСкачать

ФИЗИКА ОГЭ 2024 ВАРИАНТ 27 КАМЗЕЕВА РАЗБОР ЗАДАНИЙ I Эмиль Исмаилов - Global_EEСкачать

Урок 28 (осн). Вычисление массы и объема тела по плотностиСкачать

Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

ФИЗИКА ЕГЭ 2024 ВАРИАНТ 3 ДЕМИДОВА РАЗБОР ЗАДАНИЙ I Эмиль Исмаилов - Global_EEСкачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Урок 315. Решение задач динамикиСкачать

ФИЗИКА ОГЭ 2024 ВАРИАНТ 26 КАМЗЕЕВА РАЗБОР ЗАДАНИЙ I Эмиль Исмаилов - Global_EEСкачать

ФИЗИКА ЕГЭ 2024 ВАРИАНТ 10 ДЕМИДОВА РАЗБОР ЗАДАНИЙ I Эмиль Исмаилов - Global_EEСкачать

	Тесты по физике взяты из сборника экзаменационных заданий физика ЕГЭ 2008 г. МЕХАНИКА В. Задания повышенного уровня сложности
	Задание 1.1-В1. Груз массой т = 0,2 кг привязан к нити длиной 1 = 1 м. Нить с грузом отвели на угол 60° (см. рис.). Чему равна кинетическая энергия груза при прохождении им положения равновесия? Полученный ответ округлить до целых Рекомендации по решению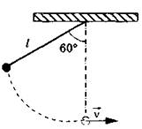
	Задание 1.1-В2. Тело массой 1 кг бросили с поверхности Земли со скоростью 20 м/с под углом 45° к горизонту. Чему равна работа силы тяжести за время полета тела (от броска до падения на Землю)? Сопротивлением воздуха пренебречь. Рекомендации по решению Задание 1.1-ВЗ. Сани с седоками общей массой 100 кг съезжают с горы высотой 8 м и длиной 100 м. Какова средняя сила сопротивления движению санок, если в конце горы они достигли скорости 10 м/с, а начальная скорость равна нулю? Рекомендации по решению Задание 1.1-В4. Груз массой 0,1 кг привязали к нити длиной 1 м. Нить отвели от вертикали на угол 90°, и груз отпустили. Каково центростремительное ускорение груза в момент, когда нить образует с вертикалью угол 60°? Сопротивлением воздуха пренебречь. Рекомендации по решению Задание 1.1-В5. Тело массой 0,1 кг колеблется так, что проекция ах ускорения его движения зависит от времени в соответствии с уравнением ах = 10sin(2πt/10) . Чему равна проекция силы на ось ох, действующей на тело в момент времени t =5/6 с? Умножьте ответ на 10. Рекомендации по решению
	С. Задания, требующие развернутого ответа
	Задание 1.1-С1. Два тела массой М подвешены на невесомом блоке при помощи легкой нити и находятся в равновесии. К одному из них подвесили груз массой 2М, и система пришла в движение. С какой силой груз массой 2М действует на нить, соединяющую грузы массами М и 2М? Рекомендации по решению Задание 1.1-С2. На одном конце тележки длиной l = 5м стоит человек массой т = 40 м. Масса тележки М = 60 кг. На какое расстояние относительно пола передвинется тележка, если человек перейдет с постоянной скоростью на другой ее конец? Массой колес и трением пренебречь. Рекомендации по решению Задание 1.1-СЗ. Тяжелый мячик отпустили без начальной скорости с высоты Н = 20 м, при ударе о землю он потерял часть своей кинетической энергии и долетел до верхней точки через t = 3 с после начала движения. Какая часть кинетической энергии перешла в тепло при ударе? Сопротивлением воздуха пренебречь. Рекомендации по решению
	Задание 1.1-С4. К покоящемуся на шероховатой поверхности телу приложена сила тяги F =bt, где b— постоянная величина. На рисунке представлен график зависимости ускорения тела от времени. Определить коэффициент трения скольжения. Рекомендации по решению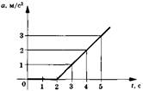
	Задание 1.1-С5. Точечные массы т 1 = 0,25 кг и т2 = 0,5 кг прикреплены к невесомому стержню длиной l— 1 м, как показано на рисунке. Стержень вращается вокруг горизонтальной оси, проходящей через точку O. В какой-то момент времени груз массой т 1 имеет скорость v 1 = 1 м/с. Определить силу, с которой стержень действует на массу т2 в этот момент времени. Рекомендации по решению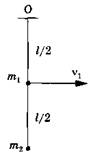
	РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ТЕСТОВЫХ ЗАДАНИЙ
	В. Задания повышенного уровня сложности Задание 1.1-В1. Воспользоваться законом сохранения механической энергии (сопротивлением воздуха пренебрегаем, а сила натяжения нити работы не совершает, так как в каждый момент времени во время движения направлена перпендикулярно вектору скорости): Еп 1 = Ек 2 , где Еп 1 — потенциальная энергия груза в верхнем (первом) положении; Ек 2 — кинетическая энергия груза в нижнем (втором) положении. Учтено, что в верхнем положении скорость груза равна нулю, а за нулевой уровень отсчета потенциальной энергии груза в поле силы тяжести Земли принят уровень груза в нижнем положении. Тогда Еп 2 = mgh = mg(l-lcosa) = mgl(1 — cosa), где h — разница высот груза в верхнем и нижнем положениях. К задаче Задание 1.1-В2. Воспользоваться свойством потенциальных сил, работа которых не зависит от формы траектории, а зависит только от начального и конечного положений тела. В качестве траектории взять соединяющий начальное и ко­нечное положения отрезок прямой, расположенной параллельно поверхности Земли. Тогда работа сила тяжести равна А = mgScosa, где mg — модуль силы тяжести; S — дальность полета тела; a — угол между вертикально направленной силой тяжести и горизонтальным направлением вектора перемещения тела. Поскольку a = 90°, то А = 0 К задаче Задание 1.1-ВЗ. Применить закон изменения механической энергии: ΔЕ = Е 2 — Е 1 = A Fc . Е1 = mgh — механическая энергия саней в первом (верхнем) состоянии, когда их скорость и, следовательно, кинетическая энергия равна нулю, т = 100 кг — масса саней, h = 8 м — высота горы. Е2 =mv 2 /2 механическая энергия саней во втором (нижнем) состоянии, где v = 10 м/с — скорость саней в этом состоянии. Работа силы сопротивления при спуске саней с горы рассчитывается по формуле: A Fc = FcScosa , где Fc — искомая сила сопротивления движению санок; S = 100 м — длина горы; a=180° — угол между направлением силы сопротивления и направлением вектора перемещения саней. К задаче Задание 1.1-В4. Использовать формулу для расчета центростремительного ускорения ацс= v 2 /R , где v — модуль вектора скорости груза; R =l = 1 м — радиус окружности, по которой он движется. Для нахождения величины v применить закон сохранения механической энергии (сопротивлением воздуха пренебрегаем, а сила натяжения нити работы не совершает): Е 1 =Е 2 -Е 1 — механическая энергия груза в первом (верхнем) положении; Е 2 — его механическая энергия во втором положении, когда нить образует с вертикалью угол 60°. За нулевой уровень отсчета потенциальной энергии груза в поле силы тяжести Земли примем уровень груза в нижнем положении (при прохождении им положения равновесия). Тогда Ex = mgl, где т = 0,1 кг — масса груза, a E 2 = mgh+mv 2 /2 , где h — высота груза во втором положении относительно нижне­го положения. Высота h равна h = l- lcosa = 1(1 — cosa). К задаче
	Задание 1.1-В5. Применить второй закон Ньютона для определения проекции силы: Fx = max, где m = 0,1 кг — масса тела. К задаче
	С. Задания, требующие развернутого ответа Задание 1.1-С1. Записать уравнения движения грузов в проекции на направленную вертикально вниз координатную ось, при этом учесть, что модули ускорений a грузов равны, равны по модулю силы натяжений нитей T1 между грузами массами М и силы натяжений нитей Т2 между грузами массами М и 2М. Для груза массой 2М: 2Mg — Т2 = 2Ма; для движущегося вниз груза массой М: Mg + Т2 — Т1 = Ма; для движущегося вверх груза массой М: Mg — Т1 = -Ма. Решая полученную систему уравнений, можно определить искомую величину Т2 К задаче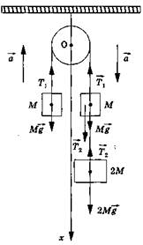
	Задание 1.1-С2. При движении человека относительно тележки со скоростью v тележка (вместе с человеком) движется в противоположную сторону со скоростью u . Применить классический закон сложения скоростей: скорость человека относительно земли равна: v 1 =v+u, а её модуль v 1 =v-u. Использовать закон сохранения импульса системы человек — тележка в системе отсчета, связанной с землей (применять закон можно, так как трения нет): m*v 1 +M*u=0. В уравнении справа стоит ноль, так как тележка покоится, если человек неподвижен. Записать закон в проекции на ось, направленную вдоль вектора скорости человека относительно тележки: m(v — u) — М*u = 0. Решить полученное уравнение относительно величины и =m*v/(M+m). Определить время движения человека по тележке: t =l/v . Найти искомую величину перемещения тележки: S = ut =m*v/(M+m)*l/v=m*l/(M+m). К задаче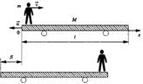
	Задание 1.1-СЗ. Определить механическую энергию мячика в начальной точке, которая равна его потенциальной энергии (так как скорость мячика в верхней точке равна нулю): Е 1 = Еп 1 = mgH. Такой же механической, но уже кинетической, энергией обладает мяч перед ударом о землю, так как сопротивлением воздуха пренебрегаем. Найти время свободного падения мяча по формуле: Н=(gt2 2 )/2 , откуда t1= √(2H/g)=√(2*20/10)=2 с . Определить время движения мяча вверх: t2= t-t1 = 3-2=1с и высоту подъема мяча после удара о землю: h =gt2 2 /2 . Рассчитать механическую (потенциальную) энергию мяча на высоте h: Е 2 =Еп 2 =mgh. Такой же механической (кинетической) энергией обладает мяч после удара о землю. Написать закон превращения части механической энергии в тепловую энергию Q при ударе о землю: Е 1 +Е 2 +Q и определить величину Q. Рассчитать, какая часть механической (кинетической) энергии перешла в тепло при ударе: Q/E 1 . К задаче Задание 1.1-С4. Из графика определить, что движение тела начинается в момент времени t 1 =2с, когда модуль приложенной силы bt 1 равен максимальной величине силы трения покоя: bt 1 =μmg, где (μ — коэффициент трения; m — масса тела. Написать второй закон Ньютона при движении тела (для моментов времени t > t 1 ) в проекции на координатную ось, направленную в сторону движения: та = bt-μmg. Учтено, что модуль силы трения скольжения равен модулю максимальной силы трения покоя. Решая систему полученных уравнений, получить выражение для коэффициента трения: μ=(at 1 )/(g(t-t 1 )). Определить из графика зависимости модуля ускорения тела от времени, что, например, для момента времени t = 3 с величина ускорения равна а = 1 м/с 2 . Подставить полученные численные значения в формулу для расчета коэффициента трения. К задаче Задание 1.1-С5. Применить второй закон Ньютона для тела массой т 2 в нижней точке в проекции на направленную вертикально вверх координатную ось: т 2 а 2 = Т — m 2 g, где а 2 = а цс — модуль вектора ускорения (центростремительного) второго тела в нижней точке; Т — искомая величина, сила, с которой стержень действует на массу т 2 в нижней точке. Сравнить линейные скорости движения грузов массами т 1 и т с помощью формулы v = ωR, где v — модуль вектора линейной скорости; ω — угловая скорость; R — радиус вращения точки. Угловые скорости закрепленных на стержне тел при вращении стержня одинаковы, а радиус вращения тела массой т 2 в 2 раза больше радиуса вращения тела массой т 1 . Поэтому v 2 = 2v 1 . Рассчитать модуль центростремительного ускорения тела массой т2 в нижней точке по формуле а цс =v2 2 /l=2v1/l=4v12/l . Решить первое уравнение относительно величины Т К задаче
	C 1 Вертикально расположенный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре 361 К. Сколько молей газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда. Толщиной поршня пренебречь. Ответ: 0,022 моль
	С1 В горизонтально расположенной трубке постоянного сечения, запаянной с одного конца, помещен столбик ртути длиной 15 см, который отделяет воздух в трубке от атмосферы. Трубку расположили вертикально запаянным концом вниз и нагрели на 60 К. При этом объем, занимаемый воздухом, не изменился. Давление атмосферы в лаборатории- 750 мм рт.ст. Какова температура воздуха в лаборатории? Ответ: T 0 =300К