Граничные условия для дифференциальных уравнений (2 видео)

Содержание

Начальные и граничные условия
Введение
Небольшой пример
Классификация граничных условий
Заключение
Дифференциальные уравнения в частных производных¶
Эллиптические уравнения¶
Параболические уравнения¶
Гиперболические уравнения¶
Начальные и граничные условия¶
🔍 Видео

Видео:Геометрический смысл дифференциального уравненияСкачать

Начальные и граничные условия

Здравствуйте, продолжаем нашу рубрику по дифференциальным уравнениям, это уже 2 статья, если вы хотите начать сначала и ознакомиться с видами дифференциальных уравнений, то вам в первую статью.

Введение

Итак, для использования численных методов при решении дифференциального уравнения необходимо дополнительные условия. Если искомая функция(концентрация, температура и т.д) является функцией времени u=u(t), то требуются начальные условия, которые являются значением этой функции в момент времени, принятый за начальный:

Если начальная функция также зависит и от пространственных координат u=u(t,x), то начальное условие характеризуют ее распределение в пространстве в начальный момент времени:

В последнем случае помимо начальных условий требуются еще и граничные условия, которые имеют значения функции u(t,x) на границе изучаемой системы для любого момента времени. Причем, если искомая функция зависит от нескольких пространственных координат, то необходимо задавать граничные условия по каждой из них.

Небольшой пример

Например для следующего уравнения:

начальное условие
2 граничных условия по координате
1 граничное условие по координате
2 граничных условия по координате

Сразу же возникает вопрос, почему именно так? Так вот, порядок производной определяет количество граничных условий для переменной. Как вы заметили, по y присутствует только первая производная, поэтому и одно граничное условие.

Классификация граничных условий

Для лучшего понимания рассмотрим классификацию на примере уравнения:

будет изменятся от до , соответственно при , будет левая граница, а при , будет правая.

Граничные условия 1-ого рода

Записываются следующим образом:

— функции, зависящие от , как пример:

Граничные условия 2-ого рода

Здесь вместо самих функций используются их первые производные.

Граничные условия 3-ого рода

Смешанные граничные условия

В этом случае левое и правое граничные условия могут быть разных родов:

Заключение

На этом мы подходим к концу нашей статьи. Сегодня мы с вами изучили начальные и граничные условия в дифференциальных уравнениях. Если вам что то осталось непонятным, то это нормально, не пугайтесь. В будущих статьях мы будем еще подробнее разбираться с этими и другими тонкостями, ну а на сегодня это все.

Спасибо, что прочитали статью, если у вас остались вопросы, то задавайте их в комментариях.
И, буду вам очень признателен, если вы вступите в нашу группу вконтакте, ссылка на которую размещена слева вверху под названием сайта.

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Дифференциальные уравнения в частных производных¶

Дифференциальные уравнениями в частных производных с дополнительными уравнениями, выражающими граничные и начальные условия описывают большинство физических процессов. В общем случае линейное дифференциальное уравнение в частных производных второго порядка имеет вид

Классификация проводится в соответствии с характеристическими кривыми второго порядка для данных уравнений. По соотношению значений a, b и c уравнение относят к эллиптическим, параболическим или гиперболическим в данной точке. Тип ДУ определяется знаком выражения, называемого дискриминантом: (D(x,y) = b^2-4ac) .

Если (D(x, y) , дифференциальное уравнение является эллиптическим в точке (x, y).
Если (D(x, y) = 0) , дифференциальное уравнение является параболическим в точке (x, y).
Если (D(x, y) > 0) , дифференциальное уравнение является гиперболическим в точке (x, y).

Если коэффициенты a, b, c постоянные и значение D не зависит от точки, то в зависимости от знака D уравнение является полностью эллиптическим, гиперболическим или параболическим. В случае если коэффициенты не являются постоянными, для одного и того же уравнения возможны области, в которых оно является уравнением разного типа.

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Эллиптические уравнения¶

Эллиптическими уравнениями являются уравнения Лапласа и Пуассона, возникающие в теории потенциала для электрического поля. Так же к уравнению этого тапа сводятся многие стационарные (установившиеся) решения параболических и гиперболических задач.

Простейший вид Эллиптического уравнения:

Такими уравнения описываются стационарное распределение температуры в процессе теплопереноса и стационарное распределение концентрации при диффузии. К уравнению Лапласа приводят и многие другие задачи, например, задача о распределении электростатического поля в однородной непроводящей среде в отсутствие электрических зарядов. В общем случае в векторной форме уравнение Пуассона имеет вид:

где (u(x, y, z)) – искомая функция; (A(x, y, z)) , (f(x, y, z)) – некоторые функции независимых переменных. Функция А описывает «коэффициент распространения» величины u и может являться тензорной величиной в случае анизотропной среды. Функция f это функция источников – скалярная величина, показывающая плотность «скорости появления» величины u в единице объема. В качестве величин, входящих в это уравнение могут использоваться, температура, коэффициент теплопроводности, плотность тепловых источников или потенциал эл. поля, диэлектрическая проницаемость и плотность зарядов и т.д

Видео:Дифференциальные уравнения на службе у борцовСкачать

Параболические уравнения¶

Параболические уравнения появляются в нестационарных задачах теплопроводности, диффузии, иногда параболические задачи получаются из гиперболических уравнений (параболическое приближение в оптике) и т. д. Уравнение теплопроводности, например, имеет вид:

В первом слагаемом коэффициенты это плотность и удельная теплоемкость, во втором слгаемом – коэффициент теплопроводности, правая часть – плотность источников тепла.

Видео:2.5 Граничные условия для векторов поля на поверхности раздела средСкачать

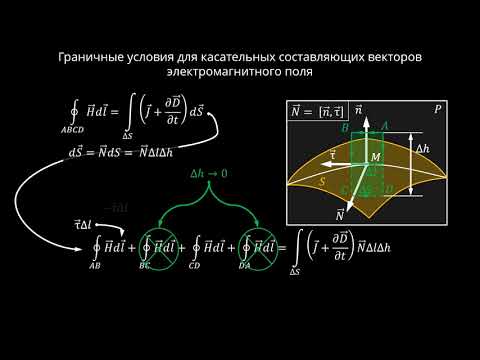
Гиперболические уравнения¶

Гиперболические уравнения, часто называют волновыми уравнениями, т.к. с их помощью описывается распространения волн (упругих, электро — магнитных, сдвиговых). К этому же типу уравнений относится уравнение Шредингера квантовой механики.

Видео:46. Граничные условия для электрического поляСкачать

Начальные и граничные условия¶

Из курса высшей математики известно, что дифференциальные уравнения, как правило, имеют бесконечное множество решений. Это связано с появлением в процессе интегрирования констант, при любых значениях которых решение удовлетворяет исходному уравнению. Решение задач физики связано с нахождением зависимостей от координат и времени определенных физических величин, которые, безусловно, должны удовлетворять требованиям однозначности, конечности и непрерывности. Иными словами, любая задача физики предполагает поиск единственного решения (если оно вообще существует). Поэтому математическая формулировка физической задачи должна помимо основных дифференциальных уравнений, описывающих искомые функции, включать дополнительные уравнения (дифференциальные или алгебраические), описывающие искомые функции на границах рассматриваемой области в любой момент времени и во всех внутренних точках области в начальный момент времени. Эти дополнительные уравнения называют соответственно граничными и начальными условиями задачи. Условия, относящиеся к точкам пространства, называются граничными. Обычно это неизменные условия, накладываемые на значение функции или на ее производную (поток через границу) на границе рассматриваемой области. Начальные условия – условия о значениях физической величины в начальный момент времени. Только после задания обоих типов условий можно получить описание развития процесса во времени. Для ДУЧП редко решают задачи, когда условия внутри области заданы для различных моментов времени, т.к. это сильно усложняет и без того не простую процедуру поиска решения.