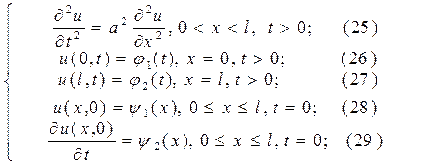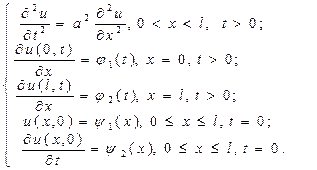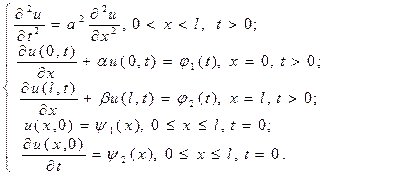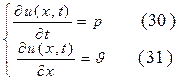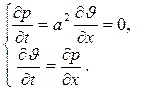Граничные и начальные условия для уравнений гиперболического типа

Дифференциальные уравнениями в частных производных с дополнительными уравнениями, выражающими граничные и начальные условия описывают большинство физических процессов. В общем случае линейное дифференциальное уравнение в частных производных второго порядка имеет вид

Классификация проводится в соответствии с характеристическими кривыми второго порядка для данных уравнений. По соотношению значений a, b и c уравнение относят к эллиптическим, параболическим или гиперболическим в данной точке. Тип ДУ определяется знаком выражения, называемого дискриминантом: (D(x,y) = b^2-4ac) .

• Если (D(x, y) , дифференциальное уравнение является эллиптическим в точке (x, y).
• Если (D(x, y) = 0) , дифференциальное уравнение является параболическим в точке (x, y).
• Если (D(x, y) > 0) , дифференциальное уравнение является гиперболическим в точке (x, y).

Если коэффициенты a, b, c постоянные и значение D не зависит от точки, то в зависимости от знака D уравнение является полностью эллиптическим, гиперболическим или параболическим. В случае если коэффициенты не являются постоянными, для одного и того же уравнения возможны области, в которых оно является уравнением разного типа.

Видео:Уравнения математической физики. Решение гиперболического уравнения методом Фурье.Скачать

Эллиптические уравнения¶

Эллиптическими уравнениями являются уравнения Лапласа и Пуассона, возникающие в теории потенциала для электрического поля. Так же к уравнению этого тапа сводятся многие стационарные (установившиеся) решения параболических и гиперболических задач.

Простейший вид Эллиптического уравнения:

Такими уравнения описываются стационарное распределение температуры в процессе теплопереноса и стационарное распределение концентрации при диффузии. К уравнению Лапласа приводят и многие другие задачи, например, задача о распределении электростатического поля в однородной непроводящей среде в отсутствие электрических зарядов. В общем случае в векторной форме уравнение Пуассона имеет вид:

где (u(x, y, z)) – искомая функция; (A(x, y, z)) , (f(x, y, z)) – некоторые функции независимых переменных. Функция А описывает «коэффициент распространения» величины u и может являться тензорной величиной в случае анизотропной среды. Функция f это функция источников – скалярная величина, показывающая плотность «скорости появления» величины u в единице объема. В качестве величин, входящих в это уравнение могут использоваться, температура, коэффициент теплопроводности, плотность тепловых источников или потенциал эл. поля, диэлектрическая проницаемость и плотность зарядов и т.д

Видео:Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Параболические уравнения¶

Параболические уравнения появляются в нестационарных задачах теплопроводности, диффузии, иногда параболические задачи получаются из гиперболических уравнений (параболическое приближение в оптике) и т. д. Уравнение теплопроводности, например, имеет вид:

В первом слагаемом коэффициенты это плотность и удельная теплоемкость, во втором слгаемом – коэффициент теплопроводности, правая часть – плотность источников тепла.

Видео:3.2 Решение уравнений гиперболического типа методом характеристикСкачать

Гиперболические уравнения¶

Гиперболические уравнения, часто называют волновыми уравнениями, т.к. с их помощью описывается распространения волн (упругих, электро — магнитных, сдвиговых). К этому же типу уравнений относится уравнение Шредингера квантовой механики.

Видео:Классические точные аналитические методы решения уравнений гиперболического и параболического типаСкачать

Начальные и граничные условия¶

Из курса высшей математики известно, что дифференциальные уравнения, как правило, имеют бесконечное множество решений. Это связано с появлением в процессе интегрирования констант, при любых значениях которых решение удовлетворяет исходному уравнению. Решение задач физики связано с нахождением зависимостей от координат и времени определенных физических величин, которые, безусловно, должны удовлетворять требованиям однозначности, конечности и непрерывности. Иными словами, любая задача физики предполагает поиск единственного решения (если оно вообще существует). Поэтому математическая формулировка физической задачи должна помимо основных дифференциальных уравнений, описывающих искомые функции, включать дополнительные уравнения (дифференциальные или алгебраические), описывающие искомые функции на границах рассматриваемой области в любой момент времени и во всех внутренних точках области в начальный момент времени. Эти дополнительные уравнения называют соответственно граничными и начальными условиями задачи. Условия, относящиеся к точкам пространства, называются граничными. Обычно это неизменные условия, накладываемые на значение функции или на ее производную (поток через границу) на границе рассматриваемой области. Начальные условия – условия о значениях физической величины в начальный момент времени. Только после задания обоих типов условий можно получить описание развития процесса во времени. Для ДУЧП редко решают задачи, когда условия внутри области заданы для различных моментов времени, т.к. это сильно усложняет и без того не простую процедуру поиска решения.

Видео:Уравнения математической физики. Лекция 5: Уравнения гиперболического типа (I). Лектор Хохлов Н.А.Скачать

Постановка задачи для уравнения гиперболического типа

Классическим примером уравнения гиперболического типа является волновое уравнение, которое имеет вид:

, 0 0 (24)

В данном случае искомая функция u(x, t) описывает малые продольные или поперечные колебания стержня или туго натянутой струны, точкам которых в начальный момент времени t =0 сообщили начальное смещение y₁(t)и скорость y₂(t). В случае продольных колебаний параметр a характеризует скорость звука в материале, из которого изготовлен стержень, а для поперечных колебаний параметр a связан с массой единицы длины струны и силой её натяжения.

Первая начально-краевая задача. Если концы стержня движутся по заданным законам, то есть на концах заданы перемещения (значения искомой функции), то первая начально-краевая задача для волнового уравнения имеет вид:

При постановке первой начально-краевой задачи для волнового уравнения условием (28) задаётся начальное распределения значений искомой функции u(x, t) (характеризующей смещение точек стрежня или струны), а условием (29) задаётся ещё и начальная скорость такого смещения.

Вторая начально-краевая задача. Если на концах стержня заданы значения силы, которая по закону Гука пропорциональна производной перемещения по пространственной переменной (т.е. на концах заданы значения первых производных по пространственной переменной x), то ставится вторая начально-краевая задача для волнового уравнения:

В условиях, когда концы стержня свободны, то функции j ₁(t) = j ₂(t) = 0.

Третья начально-краевая задача. Если концы стержня или струны закреплены упруго, т.е. на концевые заделки действуют силы, пропорциональные перемещениям, то ставится третья начально-краевая задача для волнового уравнения

Аналогично ставятся двумерные трехмерные начально-краевые задачи для двумерного и трёхмерного волнового уравнения.

Замечание. Необходимо отметить, что волновое уравнение (24) легко трансформируется в систему уравнений акустики (13), являющихся простейшей линейной моделью газодинамических течений. Действительно, введём следующие обозначения:

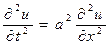
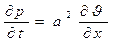
Продифференцируем уравнение (30) по переменной t, а уравнение (31) по переменной x и подставим результат в волновое уравнение , при этом получим:

(32)

Далее продифференцируем уравнение (30) по переменной x, а уравнение (31) по переменной t ,в результате будем иметь:

и

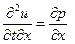
Полагая далее, что смешанные производные от u(x, t) по переменным x и t не зависят от порядка дифференцирования, получим:

(33)

Полученную систему уравнений (32), (33):

называют уравнениями акустики, как уже отмечалось выше, функции p и J характеризуют возмущения (т.е. слабые колебания) давления и скорости в акустической волне.

Видео:6.1 Смешанные краевые задачи для уравнений гиперболического и параболического типов. Метод Фурье.Скачать

Метод характеристик при решение задачи коши для уравнений гиперболического типа

Стерлитамакский филиал Башкирский государственный университет

NovaInfo58, с. 11-15
Опубликовано 25 января 2017
Раздел: Физико-математические науки
Просмотров за месяц: 83
CC BY-NC

Видео:УМФ. Метод Фурье для параболического уравненияСкачать

Аннотация

В статье рассматривается решение задачи Коши для уравнения гиперболического типа. Продемонстрировано решение данного уравнения методом характеристик.

Видео:Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Ключевые слова

Видео:Принцип максимума для параболического уравнения (Часть 2)Скачать

Текст научной работы

Многие задачи физики, в частности механики, приводят к исследованию дифференциальных уравнений в частных производных второго порядка. Так, например, при изучении различных видов волн: звуковых, электромагнитных и других колебательных явлений приходят к волновому уравнению

где u=u(x,y,z,t), a — скорость распространения волны в данной среде. В одномерном случае это уравнение примет вид

которое является уравнением вынужденных колебаний однородной струны [1, 12].

В одномерном случае рассмотрим уравнение струны [2, 26]:

Задача Коши: Найти решение u(x,y) данного уравнения, удовлетворяющее начальным условиям:

Задача Коши для уравнения струны является математической моделью физической задачи о колебаниях настолько большой струны, что влияние ее концов уже не сказывается на колебаниях других точек струны. По этой причине в этой задаче отсутствуют граничные условия.

Приведем уравнение (1) к каноническому виду. Для этого составим уравнение характеристик

где A=0, 2B=e y , C=-1. Вычислим D=B^2-AC=frac<e^>>0

. Следовательно, уравнение (1) является уравнением гиперболического типа.

Подставляя в уравнение характеристик наши значения, получим:

📺 Видео

Уравнения математической физики. Лекция 3: Уравнения параболического типа. Лектор Хохлов Н.А.Скачать

Принцип максимума для Параболического уравнения (Часть 1)Скачать

Уравнения математической физики. Лекция 6: Уравнения Гиперболического типа (2). Лектор Хохлов Н.А.Скачать

Решение уравнения теплопроводности / граничные условия второго и третьего родаСкачать

MatLab. 7.7. Параболические и гиперболические уравненияСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

5.1 Задача Штурма-ЛиувилляСкачать

Задача Коши для волнового уравнения (Часть 1)Скачать

Кокотова Е.В. Уравнения математической физики. Лекция 8. Уравнения параболического типаСкачать

4.1 Колебания полуограниченной струны с закрепленным и свободным концомСкачать

8.1 Решение уравнения теплопроводности на отрезкеСкачать