Графиком уравнений системы является две прямых окружность и прямая две параболы парабола и прямая

Видео:ВСЁ ПРО ГРАФИКИ ЕГЭ 2024 (Прямая, Парабола, Окружность, Модуль, Гипербола, Корень, Области, Сдвиги)Скачать

Алгебра. 9 класс

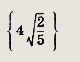
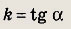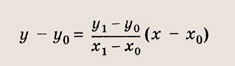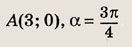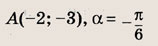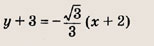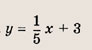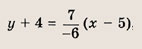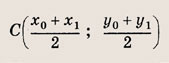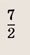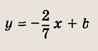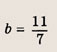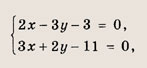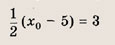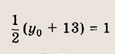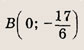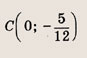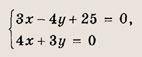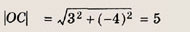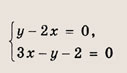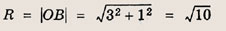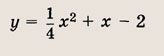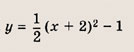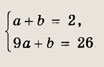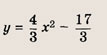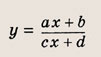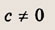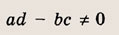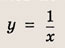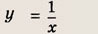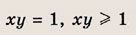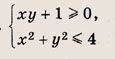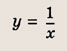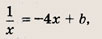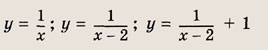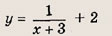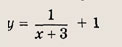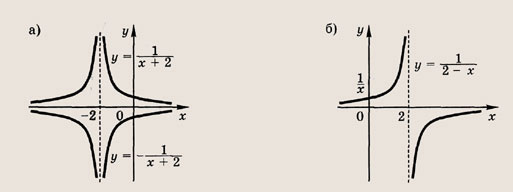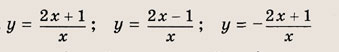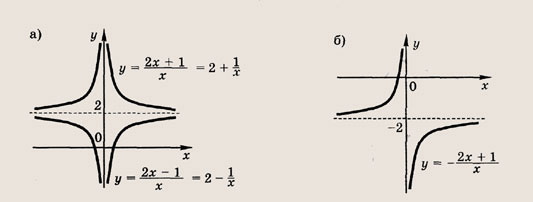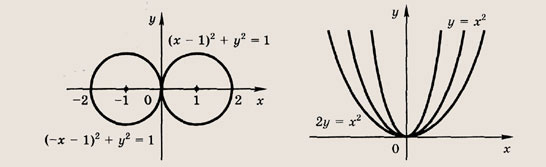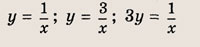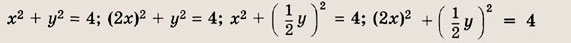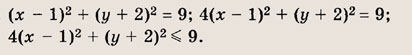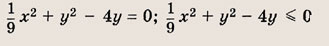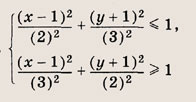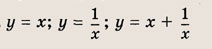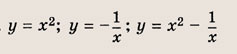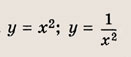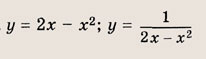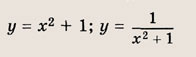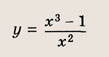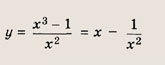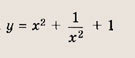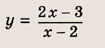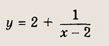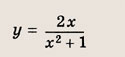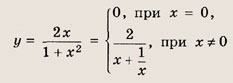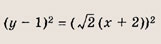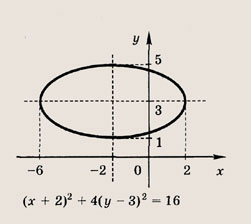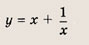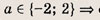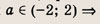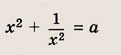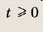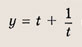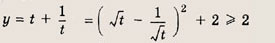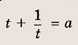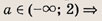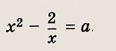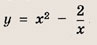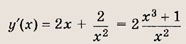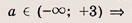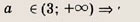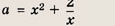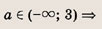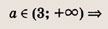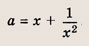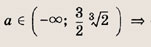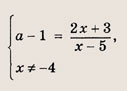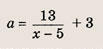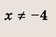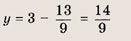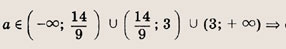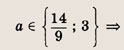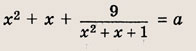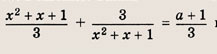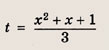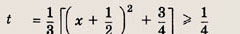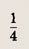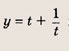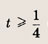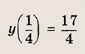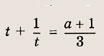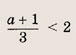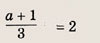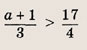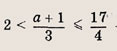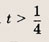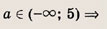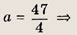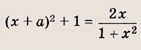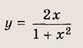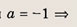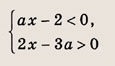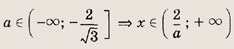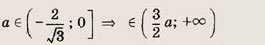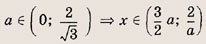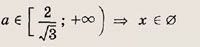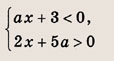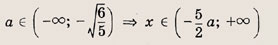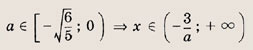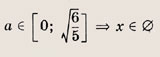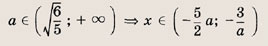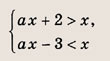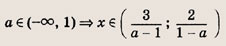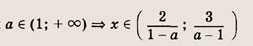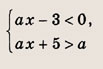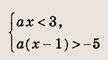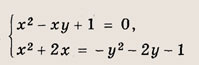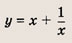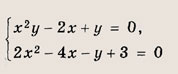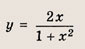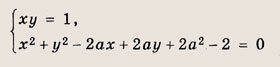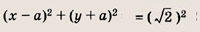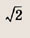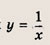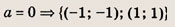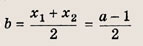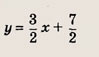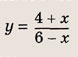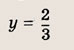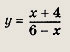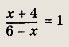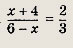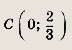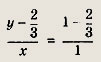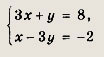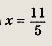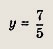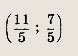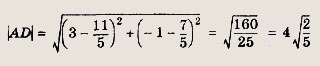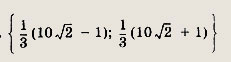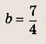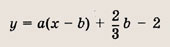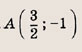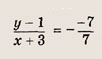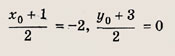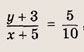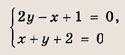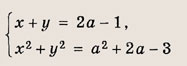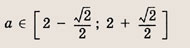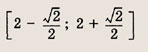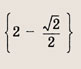Впишите пропущенное слово.

Вычеркните слово так, чтобы получилось верное утверждение.

Укажите правильный ответ.

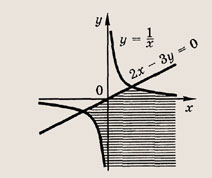
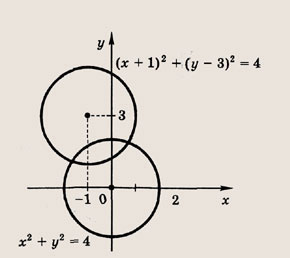
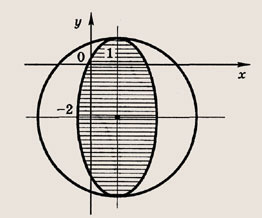
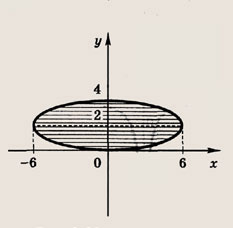
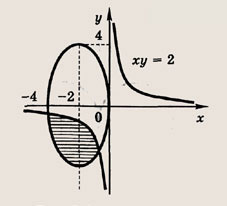
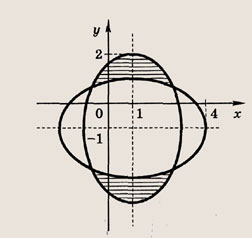
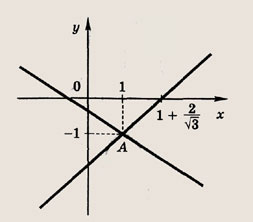
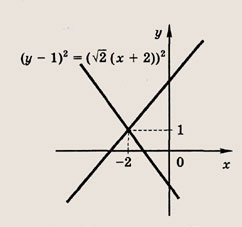
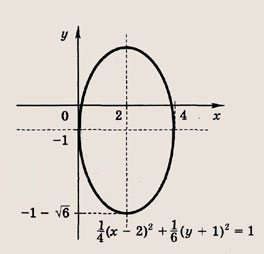
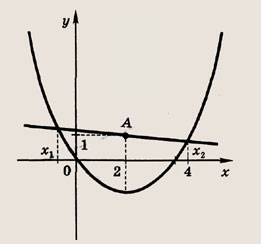
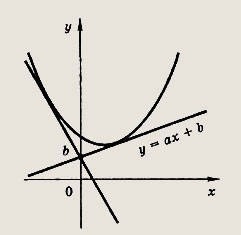
Сколько решений будет иметь система, если графики уравнений этой системы изображены на иллюстрации?

Укажите правильный ответ.

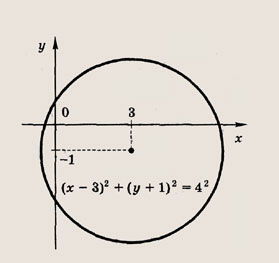
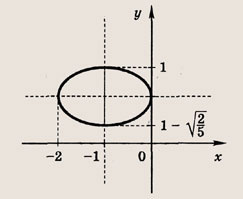
Графиком уравнений системы

является…

парабола и окружность

окружность и прямая

Укажите правильный ответ.

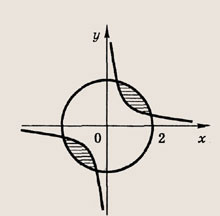
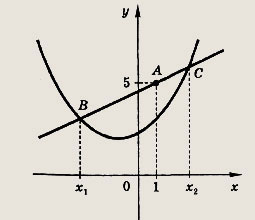
Выберите пару чисел, которая является решением системы уравнений

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Графиком уравнений системы является две прямых окружность и прямая две параболы парабола и прямая

Прямая, окружность, парабола и гипербола.
Некоторые приемы построения графиков функций

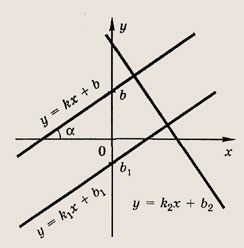
называется общим уравнением прямой. Мы уже знаем, что каждая прямая записывается таким уравнением и, обратно, каждое такое уравнение определяет прямую. Если уравнение прямой записано в виде у = kx + b, то число k называется ее угловым коэффициентом. При этом

т.е. совпадает с тангенсом угла наклона прямой L к оси Ох

Признаком параллельности двух прямых L и L₁ является равенство их угловых коэффициентов: k = k₁.

Признаком перпендикулярности прямых L и L₂ является соотношение kk₂ = -1.

y — y₀ = k(x — x₀)
‘
является уравнением прямой, проходящей через точку А(х₀; у₀) и имеющей угловой коэффициент k, а уравнание

— уравнением прямой, проходящей через две данные точки А(х₀; у₀) и В(х₁; y1).

Задание 1.

Определите точки пересечения прямой 2х — Зу — 6 = 0 с координатными осями и постройте эту прямую.

Ответ:

Задание 2.

Запишите уравнение прямой, проходящей через данную точку А(х₀; у₀) и образующей с осью Ох угол

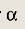
если:

а)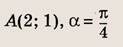

б)

в)

Ответ:

в)

Задание 3.

Запишите уравнение прямой, параллельной прямой у = 2х + 3 и проходящей через точку А(-3; 2).

Ответ:

Задание 4.

Запишите уравнение прямой, перпендикуляр,ной прямой у = -5х + 3 и проходящей через точку А(5;4)

Ответ:

Задание 5.

Запишите уравнение сторон треугольника, если известны его вершины А(5; -4), В(-1; 3) и С(-3; -2).

Используя общее уравнение прямой, проходящей через две заданные точки, для прямой (АВ) имеем

т. е. 7х + 6у — 11 = 0.

Аналогично получаем: (АС) х — 4у + 11 = 0, (ВС) 5х — 2у + 11 = 0.

Задание 6.

Запишите уравнение прямой, проходящей через точку М₁(2, 1) перпендикулярно прямой, проходящей через точки М₂(5; 3) и М₃(3; -4).

• Пусть А(х₀; у₀), B(х₁у₁) — две данные точки; тогда точка С

лежит на прямой, проходящей через точки А и В, и делит отрезок АВ пополам. Используйте этот факт при решении задний 7, 8.

Решение:

Уравнение прямой (М₂М₃) имеет вид 7х — 2у — 29 = 0. Ее угловой коэффициент равен

Поэтому уравнения прямых, перпендикулярных данной прямой, имеют вид

Подставляя в это равенство координаты точки М₁ (2; 1), находим

Отсюда следует нужное нам уравнение.

Ответ:

Задание 7.

Найдите координаты точки О, симметричной тс)чке Р(-5; 13) относительно прямой 2х — Зу — 3 = 0.

Решение:

Проведем через точку Р (-5; 13) прямую, перпендикулярную прямой 2х -Зу — 5 = 0. Ее уравнение есть Зх + 2у — 11 = 0.

Найдем координаты точки пересечения этих прямых, для чего решим систему уравнений

откуда х = 3, у = 1. Точка С(3; 1) является серединой отрезка PQ, где Р (-5; 13), a Q(x₀; у₀) — искомая точка. Поэтому

Ответ:

Задание 8.

Составьте уравнение прямой, параллельной прямым 2х + Зу -6 = 0 и 4х + 6у+ 17 = 0 и проходящей посередине между ними.

определяет окружность радиуса R с центром в точке С(х₀; у₀).

Решение:

Прямая 2х + Зу — 6 = 0 проходит через точку А(0; 2), а прямая 4х + 6у + 17 = 0 — через точку В

Следовательно, прямая, параллельная данным и проходящая посередине между ними, имеет уравнение 2х + Зу + 6 = 0 и проходит через точку C

где С — середина отрезка АВ. Отсюда находим

а тогда уравнение искомой прямой можно записать в виде:

Заметим, что это уравнение есть полусумма уравнений 8х + 12у — 24 = 0 и 8х + 12у + 34 = 0, задающих известные нам прямые.

Ответ:

Задание 9.

Запишите уравнение окружности, если:

а) центр окружности совпадает с точкой С(2; -3), а ее радиус R = 7;

б) окружность проходит через точку А(2; 6), а ее центр совпадает с точкой С(-1; 2);

в) точки А(3; 2) и В(-1; 6) являются концами одного из диаметров этой окружности.

Ответ:

а) (х — 2) 2 + (у + З) 2 = 49;

б) (х + 1) 2 + (у — 2) 2 = 25;

в) (х — 1) 2 + (у — 4) 2 = 8

Задание 10.

Запишите уравнение окружности, если ее центр совпадает с началом координат, а прямая Зх — 4у + 25 = 0 является касательной к этой окружности.

Решение:

Через начало координат О (0; 0), т. е. через центр окружности, проведем прямую, перпендикулярную прямой Зх — 4у + 25 = 0. Ее уравнение имеет вид 4х + Зу = 0. Найдем точку пересечения этих прямых, т. е. точку касания прямой Зх — 4у + 25 = 0 и искомой окружности. Решаем систему

откуда х = 3, у = -4. Таким образом, С(3; -4) — точка касания, а

— радиус искомой окружности.

Ответ:

Задание 11.

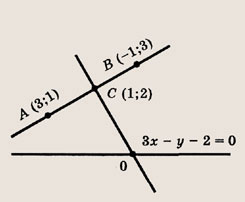
Запишите уравнение окружности, проходящей через точки А(3; 1) и Б(-1; 3), если ее центр лежит на прямой Зх — у -2 = 0.

Решение:

Центр искомой окружности О (х₀; у₀) — точка пересечения прямой Зх — у — 2 = 0 и прямой, проходящей через точку С(1;2) (середину отрезка АВ), перпендикулярно прямой (АВ)

Ее уравнение имеет вид у — 2х = 0 (см. решение задачи 6).

откуда О (2; 4). Радиус искомой окружности равен длине отрезка ОВ, т. е.

Ответ:

(х — 2) 2 + (у — 4) 2 = 10

Задание 12.

Запишите уравнение прямой, проходящей через центры двух данных окружностей:

а) (х — З) 2 + у 2 = 9, (х + 2) 2 + (у -1)2 = 1;

б) х 2 + у 2 — 4х + 6у = 0, х 2 + у 2 — 6х = 0.

Ответ:

Задание 13.

Запишите уравнения касательных к окружности х 2 + у 2 + + 2х — 19 = 0, проведенных из точки А (1; 6).

Указание:

Запишите уравнения искомых прямых в виде у = а(х — 1) + 6, подставьте у = а(х — 1) + 6 в уравнение окружности и приравняйте нулю дискриминант полученного квадратного уравнения.

Ответ:

у + 2х — 8 = 0, х — 2у + 11 =0.

Задание 14.

Установите, что каждое из следующих уравнений определяет параболу, найдите координаты ее вершины А и координаты точек пересечения с осями координат:

а)
у = 4х 2 — 8х + 7;

б)

в)
у = -х 2 + 2х + 3.

Ответ:

а) А(1; 3); с осью Ох не пересекается; С (0; 7);

Задание 15.

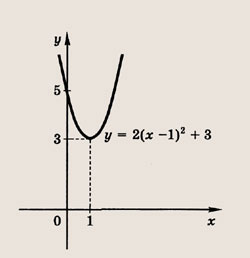
Найдите квадратный трехчлен, наибольшее значение которого, равное 3, достигается при х = 2, если известно, что его график проходит через точку О(0; 0).

Решение:

Из условия следует, что квадратный трехчлен имеет вид у = а(х — 2) 2 + 3, где а

Ответ:

Задание 16.

График квадратного трехчлена, свободный член которого равен 1, симметричен относительно прямой х + 2 = 0 и проходит через точку А(2; 7). Запишите этот квадратный трехчлен.

Ответ:

Задание 17.

Найдите квадратный трехчлен, график которого симметричен относительно прямой х = -1 и проходит через точки М₁(-2; 2) и М₂(2; 26).

Решение:

Из условия следует, что квадратный трехчлен имеет вид у = а(х + 1) 2 + b. Подставляя в это равенство координаты точек М₁(-2; 2) и М₂(2; 26), получаем систему

откуда а = 3, b = -1. Итак, у= 3(х + 1) 2 — 1 = Зх 2 + 6х + 2.

Ответ:

у = = 3х 2 + 6х + 2

Задание 18.

Найдите квадратный трехчлен, график которого симметричен относительно прямой х = 1 и проходит через точки M₁(2; -1) и М₂(-4; 47).

Ответ:

Задание 19.

Парабола у = х 2 — 4х + 2 пересекается с прямой у = х + 8 в точках А и В. Запишите уравнение параболы, проходящей через А, В и точку О(0; 0).

Находим координаты точек А и В. Решаем уравнение

х 2 — 4х + 2 = х + 8, т. е. х 2 — 5х — 6 = 0 и получаем: А (-1; 7), В (6; 14).

Уравнение искомой параболы имеет вид у = ах 2 + bх. Подставляя в это равенство координаты точек А и В, приходим к системе:

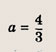
Ответ:

Задание 20.

График квадратного трехчлена, наименьшее значение которого, равное нулю, достигается при х — 1, проходит через точку А(-1; 4). Составьте уравнения касательных к этому графику, проходящих через начало координат.

Решение:

Из условия следует, что квадратный трехчлен имеет вид у = а(х — 1) 2 , где а > 0. Подставляя в это равенство координаты точки А (-1; 4), находим а = 1, откуда у = (х — 1) 2 = х 2 — 2х + 1. Уравнения всех прямых, проходящих через точку О (0; 0), имеют вид у = ах. Приравнивая нулю дискриминант квадратного уравнения х 2 — 2х + 1 = = ах, т. е. х 2 — (2 + а)х + 1 = 0, имеем D = (а + 2) 2 — 4 = а 2 + 4а = О, откуда a₁= 0, а₂ = -4. Таким образом, получаем искомые уравнения касательных: у = 0 и у = -4х.

Ответ:

Задание 21.

Запишите уравнение параболы, проходящей через данные точки А, В и С, если:

a, b, d — действительные числа и

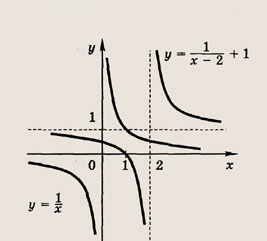
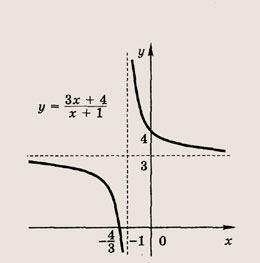
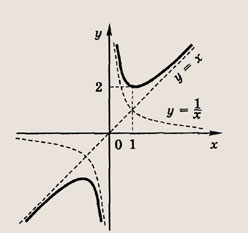
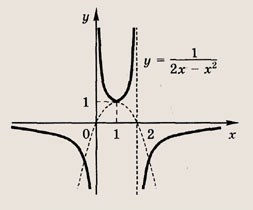
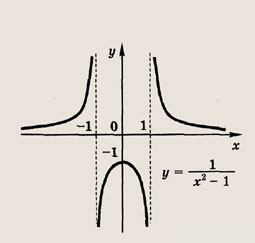
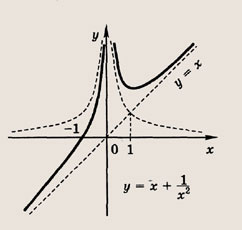
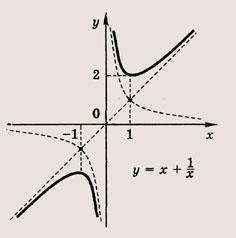
называется дробно-линейной функцией. Кривая, которая служит графиком этой функции, называется гиперболой. Ниже мы установим, что график дробно-линейной функции можно получить из графика простейшей дробно-линейной функции

(графика обратной пропорциональной зависимости) с помощью параллельного переноса,
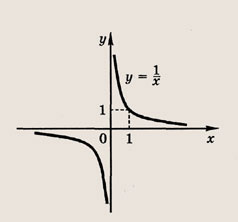
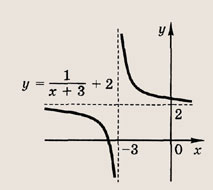
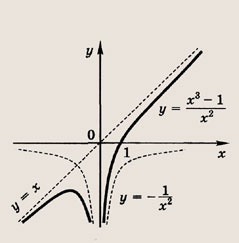
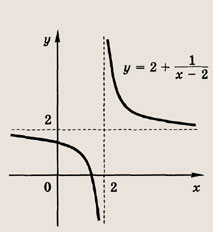
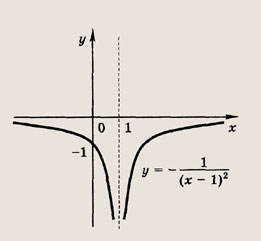
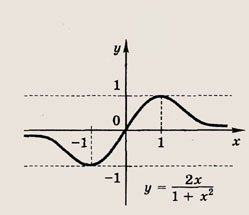
отражения и растяжения (сжатия) вдоль координатных осей. График функции

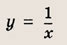
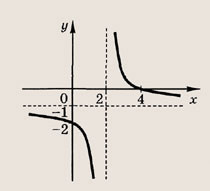
изображен на рис.

Отметим, что прямые у =0 и х=0 (координатные оси) являются асимптотами гиперболы

а точка О(0; 0) — ее центром симметрии.

Указание:

Запишите уравнение искомой параболы в виде у = ах 2 + bх + с и подставьте в это равенство координаты данных в условии точек.

Ответ:

а) у = 2х 2 — х — 1;

б) у = -х 2 + 2х + 3

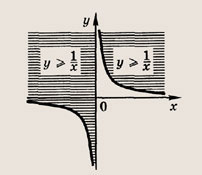
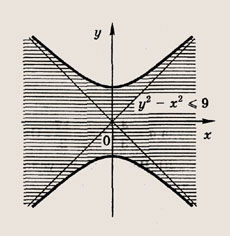
Постройте графики следующих функций и уравнений. Штриховкой укажите области, координаты точек которых удовлетворяют указанным неравенствам (22—26):

Задание 22.

Ответ:

Задание 23.

Почему в заданиях 22 и 23 получаются различные заштрихованные области?

Ответ:

Задание 24.

Ответ:

Задание 25.

Ответ:

Задание 26.

(эта кривая также является гиперболой).

Ответ:

Задание 27.

Составьте уравнения касательных к гиперболе

параллельных прямой у = -4х + 1.

Напомним некоторые приемы, которые часто используются при построении графиков функций. При этом предполагается, что график функции у = f(x) (или уравнения f(x, у) = 0) известен.

• Сдвиги (параллельные переносы) вдоль координатных осей.

Пусть построен график функции у = f(x). Тогда:

1) график функции у = f(x + а) получается из графика функции у — f(x) переносом вдоль оси Ох на а единиц
влево, если а > 0, или на |а| = -а единиц вправо, если а

2) график функции у = f(x) + b получается из графика функции у = f(x) переносом на b единиц вверх, если b > О, или на |b| = -b единиц вниз, если b

3) график уравнения f(x -а, у) = О получается из графика уравнения f(x, у) = О переносом на |а| вправо, если а > 0, и влево, если а 0, и вниз, если b

Решение:

Уравнение касательной должно иметь вид у = -4х+ b.

Приравнивая нулю дискриминант квадратного уравнения

т. е. 4х 2 — bх + 1 = 0, имеем D = b 2 — 16 = 0, т.е. b₁ = -4; b₂ = 4. Итак, получаем искомые уравнения касательных: у = -4х — 4 и у = -4х + 4.

Ответ:

у = -4х — 4; у = -4x + 4

Постройте графики следующих функций и уравнений (28—34):

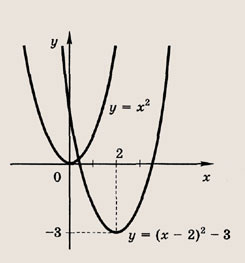
Задание 28.

у = х 2 ; у = (х — 2) 2 ; у = (х -2) 2 — 3

Ответ:

Задание 29.

х 2 + у 2 = 4; (х + 1) 2 + у 2 = 4; (х + 1) 2 + (у — З) 2 = 4

Ответ:

Задание 30..

Ответ:

Задание 31.

Ответ:

Задание 32.

х 2 — 6х + у 2 + 2у — 6 = 0

Ответ:

Задание 33.

(jc — 1)(у + 2) = 2х — 3

Указание:

Преобразуйте уравнение к виду

Ответ:

Задание 34.

Указание:

Преобразуйте уравнение к виду

Ответ:

Задание 35.

а) (х — 1) 2 + (у + 1) 2 = 4;

б) х 2 — 4х + у 2 + 6у = 0

Запишите уравнение образа каждой из них при параллельном переносе, если ее центр смещается в точку С(-1; 2).

Решение б):

Запишем уравнение данной окружности в виде (х — 2) 2 + (у + З) 2 = 13. При параллельном переносе радиус окружности не меняется. Уравнение окружности радиуса

с центром в точке С(-1;2) имеет вид (х + 1) 2 + (у — 2) 2 = 13.

Ответ:

а) (х + 1) 2 + (у — 2) 2 = 4

б) (х + 1) 2 + (у — 2) 2 = 13

Задание 36.

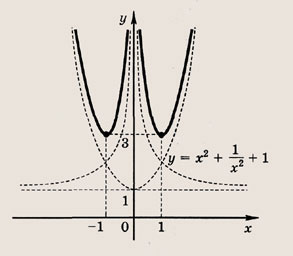
Запишите уравнение образа параболы у = х 2 + + 2х + 2 при параллельном переносе, если ее вершина смещается в точку A(x₀; у₀), где

Решение б).

Парабола у = х 2 + 2х + 2 = (х + 1) 2 + 1 получается из параболы у = х 2 переносом вершины в точку А (-1; 1). Если вершина этой параболы при параллельном переносе сместится в точку А (-3; 4), то ее уравнение примет вид у = (х + З) 2 + 4.

б) у = х 2 + 6х + 13

в) у = х 2 + 2х + 2

Ответ:

Задание 37.

Запишите уравнение образа гиперболы

при параллельном переносе, если ее центр симметрии смещается вточку А(-3; 1).

• Зеркальное отражение относительно координатных осей.

Пусть задан график функции у = f(x) (или уравнения f(x, у) = 0). Тогда:

1) графики функций у = f(x) и у = f(-x) (уравнений f(x, у) = 0 и f(-x, у) = 0) симметричны относительно оси Оу,

2) графики функций у = f(x) и у = -f(x) (уравнений f(x, у) = 0 и f(x; -у) = 0) симметричны относительно оси Ох.

Постройте графики следующих функций и уравнений (38—42).

Ответ:

Задание 38.

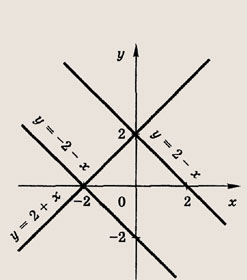
у = 2 + х; у = 2 — х; у = -(2 + х)

Ответ:

Задание 39.

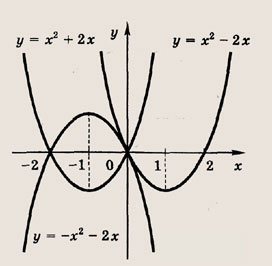
у = х 2 + 2х; у = х 2 — 2х; у = -(х 2 + 2х)

Ответ:

Задание 40.

Ответ:

Задание 41.

Ответ:

Задание 42.

(х — I) 2 + у 2 =1;(х + 1) 2 + у 2 =1

• Растяжение (сжатие) графика вдоль координатных осей.

Пусть задан график функции у = f(x) и число k > 0. Тогда:

1) график функции у = f(kx) получается из графика функции у = f(x) сжатием вдоль оси Ох в k раз, если

2) график функции у = kf(x) получается из графика функции у = f(x) растяжением вдоль оси Оу в k раз, если

Отметим также, что графики уравнений f(kx, у) = 0, f(x, ky) = 0 получаются из графика уравнения f(x, у) = 0 сжатием вдоль соответствующей координатной оси в k раз, если k > 1 (при k

Постройте графики следующих функций и уравнений (43—50). Отметьте штриховкой области, координаты точек которых удовлетворяют указанным неравенствам.

Ответ:

Задание 43.

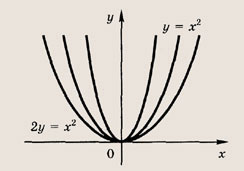
у = х 2 ; у = (2х) 2 ; 2у = х 2

Ответ:

Задание 44.

Ответ:

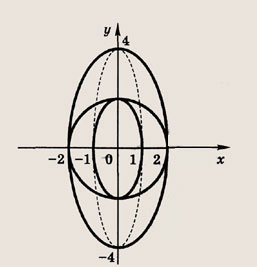
Задание 45.

(кривая, которая получается при сжатии окружности вдоль координатных осей, называется эллипсом).

Ответ:

Задание 46.

Ответ:

Задание 47.

Ответ:

Задание 48.

Ответ:

Задание 49.

Ответ:

Задание 50.

• При построении эскизов графиков элементарных функций часто используются и такие приемы, как сложение (вычитание) и деление (умножение) графиков.

Постройте графики следующих функций (51—57):

Ответ:

Задание 51.

Ответ:

Задание 52.

Ответ:

Задание 53.

Ответ:

Задание 54.

Ответ:

Задание 55.

Ответ:

Задание 56.

Указание:

Ответ:

Задание 57.

Указание:

Ответ:

Используя различные приемы, постройте графики следующих функций и уравнений (58—71):

Задание 58.

Ответ:

Задание 59.

Указание:

Ответ:

Задание 60.

Указание:

Ответ:

Задание 61.

Ответ:

Задание 62.

Ответ:

Задание 63.

Ответ:

Задание 64.

Указание:

Ответ:

Задание 65.

Указание:

Ответ:

Задание 66.

3(х — 1) 2 — 4(у + 1) 2 = 0

Указание:

Постройте две пересекающиеся прямые Зх 2 = 4у 2 , затем выполните параллельный перенос, при котором точка их пересечения сместится в точку А(1; -1).

Ответ:

Задание 67.

2х 2 — у 2 + 8х + 2у + 7 = 0

Указание:

Ответ:

Задание 68.

(х + 2) 2 + 4(у — З) 2 = 16

Ответ:

Задание 69.

Зх 2 + 2у 2 — 12х + 4у + 2= 0

Указание:

Ответ:

Задание 70.

Указание:

Ответ:

Задание 71.

ху + х — 2у — 4 = 0

Указание:

Ответ:

Найдите число различных решений уравнений в зависимости от а (72—80):

Задание 72.

Ответ:

Задание 73.

Ответ:

два решения, при

одно решение; при

Задание 74.

Решение:

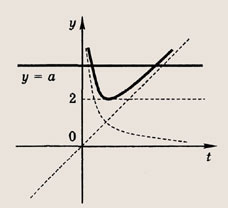
Положим х 2 = t. Тогда

Построим при t > 0 график функции

при t > 0, причем наименьшее значение у = 2 достигается при t = 1, то получаем: при
а уравнение

не имеет положительных решений, при а = 2 => одно решение; а > 2 => два решения. Теперь находим число решений исходного уравнения.

Ответ:

нет решений, при а = 2 => два решения; при

Задание 75.

Решение:

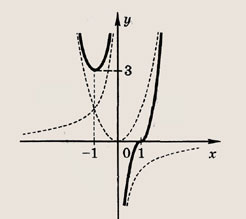
Построим график функции

то х = -1 — точки минимума функции у(х) и у(-1) = 3

Поэтому получаем следующий ответ.

Ответ:

одно решение; при а = 3 => два решения; при

Задание 76.

Указание:

Запишите уравнение в виде

Далее см. решение задачи 75.

Ответ:

одно решение; при а = 3 => два решения; при

Задание 77.

х 3 — ах 2 + 1 = 0

Запишите уравнение в виде

Ответ:

одно решение; при

два решения; при

Задание 78.

Решение:

Запишем уравнение в виде

График этой функции — гипербола, принимающая все значения, кроме у = 3, по одному разу. Поскольку

нужно также исключить значение

Ответ:

одно решение; при

Задание 79.

Решение:

Запишем уравнение в виде

Сначала найдем число решений уравнения

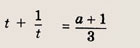
не меньших

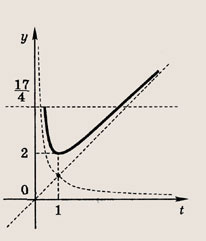
Построим график функции

а наименьшее значение y(t) равно 2. Поэтому уравнение

не имеет решении, при

— имеет одно решение, а при

— два решения, удовлетворяющих условию

Отдельно рассмотрим случай

имеет одно решение (мы находим число различных решений). При всех остальных

уравнение х 2 + х + 1 = 3t будет иметь два различных решения. Теперь легко записываем ответ.

Ответ:

нет решений; при

два решения; при

четыре решения; при

Задание 80.

(х 2 + 1)(х 2 + 2ах + а 2 + 1) = 2х

Указание:

Запищите уравнение в виде

и постройте графики функций

Ответ:

одно решение х = 1, при других а решений нет.

Решите системы неравенств и уравнений (81—87):

Задание 81.

Ответ:

Задание 82.

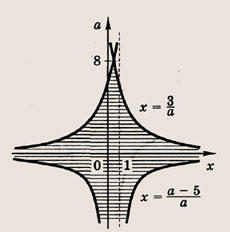
Решение:

На координатной плоскости (х, а) штриховкой отметим точки, координаты которых удовлетворяют нашей системе неравенств

Ответ:

Задание 83.

Ответ:

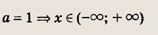
при

Задание 84.

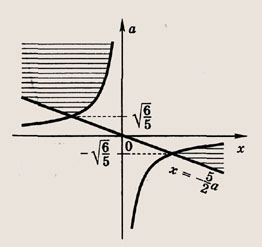
Решение:

Перепишем неравенства в виде

и штриховкой на координатной плоскости (х; а) отметим точки, координаты которых удовлетворяют этой системе неравенств

Записываем решение данной системы.

Ответ:

Задание 85.

Указание:

и (х + 1) 2 + (у + 1) 2 =1

Ответ:

Задание 86.

Указание:

Постройте графики функций

и у = 2х 2 — 4х + 3

Ответ:

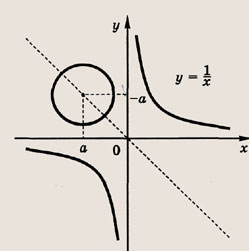
Задание 87.

Решение:

Запишем второе уравнение в виде

Это окружность радиуса

с центром (а; -а), лежащим на прямой у = -х

Пересечение с гиперболой

возможно только в том случае, если а = 0. При а = 0 получаем решения х₁ = 1, у₁ = 1 и х₂ = -1, у₂ = -1.

Ответ:

при других а решений нет.

Задание 88.

Прямая проходит через точку А(2; 1) и пересекает параболу у = х 2 — 4х в точках, сумма квадратов абсцисс которых наименьшая. Запишите уравнение этой прямой.

Решение:

Запишем уравнение прямой в виде у = а(х — 2) + 1. Тогда точки пересечения этой прямой и параболы у = х 2 — 4х

имеют абсциссы x₁и х₂, являющиеся корнями квадратного уравнения

а(х — 2) + 1 = х 2 — 4х, т. е. х 2 — (а + 4)х + 2а — 1 = 0. Так как

х₁ 2 + х₂ 2 = (x₁ + х₂) 2 — 2х₁х₂ = (а + 4) 2 — 2х₁х₂ = (а + 4) 2 — 2(2а — 1) = а 2 + 4а + 18 = (а + 2) 2 + 14, то наименьшее значение сумма квадратов абсцисс принимает при а = -2.

Ответ:

Задание 89.

Прямая проходит через точку А(1; 5) и пересекает параболу у = х 2 + х+1 в точках, сумма ординат которых наименьшая. Запишите уравнение этой прямой.

Решение:

Запишем уравнение прямой в виде у = а(х — 1) + 5. Тогда точки В и С пересечения этой прямой с параболой у = х 2 + х + 1

имеют абсциссы x₁ и х₂, являющиеся корнями квадратного уравнения

а(х — 1) + 5 = х 2 + х + 1, т. е. х 2 — (а — 1)х + а — 4 = 0.

а сумма ординат точек пересечения равна

Следовательно, сумма ординат наименьшая при

Искомое уравнение имеет вид

Ответ:

Задание 90.

Прямая проходит через точку Б(1; -3) и пересекает параболу у — 2х — х 2 в точках, сумма ординат которых наибольшая. Запишите уравнение этой прямой.

Ответ:

Задание 91.

Найдите длину перпендикуляра, опущенного из точки А(3; -1) на прямую, пересекающую линию

и проходящую через точки этой линии с ординатами у = 1 и

Решение:

Находим точки В и С пересечения прямой с кривой

откуда х= 1, т.е. В (1; 1);

откуда х = 0, т. е.

Записываем уравнение прямой, проходящей через точки В и С:

т. е. х — Зу + 2 = 0. Уравнение перпендикуляра к этой прямой, проходящего через точку А (3; -1), имеет вид у = -Зх + 8. Теперь найдем координаты точки пересечения этих прямых, для чего решим систему уравнении:

Вычисляем расстояние между точками А(3;-1) и D

Ответ:

Задание 92.

Найдите длину перпендикуляра, опущенного из точки А(5; 0) на касательную к параболе у = х 2 + 3, проведенную из точки В(0; 1).

Ответ:

Задание 93.

На оси ординат найдите точку, через которую проходят две взаимно перпендикулярные касательные к графику функции

Решение:

Уравнение касательной имеет вид у = ах + b

Приравнивая нулю дискриминант квадратного уравнения

х 2 — 2х + 3 = ах + b, т. е. х 2 — (а + 2)х + 3 — b = 0,

получим D = (а + 2) 2 — 4(3 — b) = 0, т. е. а 2 + 4а + 4b — 8 = 0.

Это уравнение должно иметь корни a₁ и а₂ такие, что а₁а₂ = -1 (а₁ и а₂ — угловые коэффициенты искомых касательных; записано условие перпендикулярности этих прямых).

Но а₁а₂= 4b — 8, т. е. 4b -8 = -1, откуда

Ответ:

Задание 94.

На прямой 2х — Зу = 6 найдите точку, через которую проходят две взаимно перпендикулярные касательные к графику функции

Указание:

Запишите уравнения касательных в виде

Далее см. решение задачи 93.

Ответ:

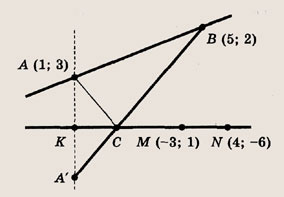
Задание 95.

На координатной плоскости даны точки А(1; 3) и В(5; 2). На прямой, проходящей через точки М(-3; 1) и
N (4; -6), найдите такую точку С, чтобы сумма длин отрезков АС и СВ была наименьшей.

Решение:

— это точка пересечения прямых (MN) и (А’В), где А’ — точка, симметричная A относительно прямой (MN) (см. задачу 7). Подумайте, почему это так? Теперь последовательно находим:

1) уравнение прямой (MN):

2) уравнение прямой (АА’):

3) координаты точки К, т. е. точки пересечения прямых (MN) и (АА):

4) координаты точки А (х0, у0); имеем

5) уравнение прямой (А’В):

т. е. 2у — х + 1 = 0;

6) координаты искомой точки С:

откуда х = -1, у = -1

Ответ:

Задание 96.

Даны точка А(5; 7) и угол, уравнения сторон которого имеют вид у = 0 и у = х+5. Точки В и С лежат на разных сторонах угла. Найдите наименьшее значение периметра треугольника ABC.

Указание:

Наименьший периметр треугольника ABC равен длине отрезка PQ, где Р — точка, симметричная А относительно прямой у = 0, a Q — точка, симметричная А относительно прямой у = х + 5.

Ответ:

Задание 97.

Числа х, у и а удовлетворяют системе уравнений

При каком значении а произведение ху принимает наименьшее возможное значение?

Указание:

Сначала выясните, при каких а данная система имеет решение. Эти значения

Далее из системы выразите произведение ху через а и найдите минимум полученной функции на отрезке

Ответ

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Алгебра. Урок 5. Графики функций

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Декартова система координат

• Функция

Видео:Как запомнить графики функцийСкачать

Декартова система координат

Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.

Координатные оси – прямые, образующие систему координат.

Ось абсцисс (ось x ) – горизонтальная ось.

Ось ординат (ось y ) – вертикальная ось.

Видео:Графики в ОГЭ по математике за 10 секунд #умскул #огэматематика #огэСкачать

Функция

Функция – это отображение элементов множества X на множество Y . При этом каждому элементу x множества X соответствует одно единственное значение y множества Y .

Видео:Графики функций. Задание №11 | Математика ОГЭ 2023 | УмскулСкачать

Прямая

Линейная функция – функция вида y = a x + b где a и b – любые числа.

Графиком линейной функции является прямая линия.

Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :

Если a > 0 , прямая будет проходить через I и III координатные четверти.

b – точка пересечения прямой с осью y .

Если a 0 , прямая будет проходить через II и IV координатные четверти.

b – точка пересечения прямой с осью y .

Если a = 0 , функция принимает вид y = b .

Отдельно выделим график уравнения x = a .

Важно : это уравнение не является функцией так как нарушается определение функции ( функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y ). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y . Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

Видео:Как получить легкий балл на ОГЭ? / Подробный разбор заданий с графиками функций по математикеСкачать

Парабола

Графиком функции y = a x 2 + b x + c является парабола .

Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :

1. Коэффициент a указывает на то, куда направлены ветки параболы.

• Если a > 0 , ветки параболы направлены вверх.
• Если a 0 , ветки параболы направлены вниз.

1. Коэффициент c указывает, в какой точке парабола пересекает ось y .
2. Коэффициент b помогает найти x в – координату вершины параболы.

1. Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .

• Если D > 0 – две точки пересечения.
• Если D = 0 – одна точка пересечения.
• Если D 0 – нет точек пересечения.

Видео:График функции y=x² (y=аx).Скачать

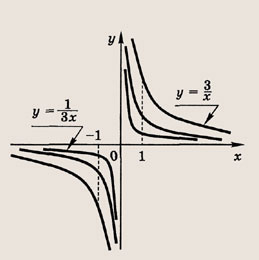
Гипербола

Графиком функции y = k x является гипербола .

Характерная особенность гиперболы в том, что у неё есть асимптоты.

Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.

Ось x – горизонтальная асимптота гиперболы

Ось y – вертикальная асимптота гиперболы.

На графике асимптоты отмечены зелёной пунктирной линией.

Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.

0″ height=»346″ width=»346″ sizes=»(max-width: 346px) 100vw, 346px» data-srcset=»/wp-content/uploads/2017/01/Гипербола-1.png 346w,/wp-content/uploads/2017/01/Гипербола-1-150×150.png 150w,/wp-content/uploads/2017/01/Гипербола-1-300×300.png 300w,/wp-content/uploads/2017/01/Гипербола-1-176×176.png 176w,/wp-content/uploads/2017/01/Гипербола-1-60×60.png 60w, https://epmat.ru/wp-content/uploads/2017/01/Гипербола-1.png»>

Если k 0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .

Видео:Квадратичная функция и ее график. 8 класс.Скачать

Квадратный корень

Функция y = x имеет следующий график:

Видео:ДВЕ ПАРАБОЛЫ / функции тип 9 / ЕГЭ #профиль #509253Скачать

Возрастающие/убывающие функции

Функция y = f ( x ) возрастает на интервале , если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)

Примеры возрастающих функций:

Функция y = f ( x ) убывает на интервале , если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).

Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции , находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции , находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.

Видео:Графики сложных функций. Подготовка к ОГЭ. Задание № 22. Вебинар | МатематикаСкачать

Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.

🎦 Видео

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Алгебра 9 класс. Графическое решение систем уравненийСкачать

Составляем уравнение прямой по точкамСкачать

10 задание. Все графики ЕГЭ по математике 2023Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Алгебра 7 класс. 3 октября. Строим график линейной функцииСкачать

Построить график ЛИНЕЙНОЙ функции и найти:Скачать