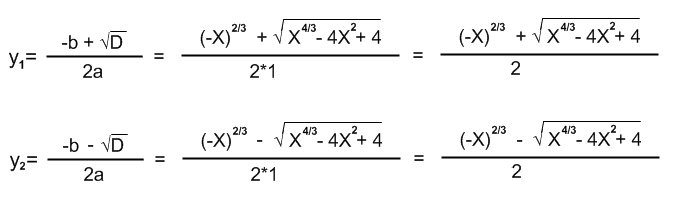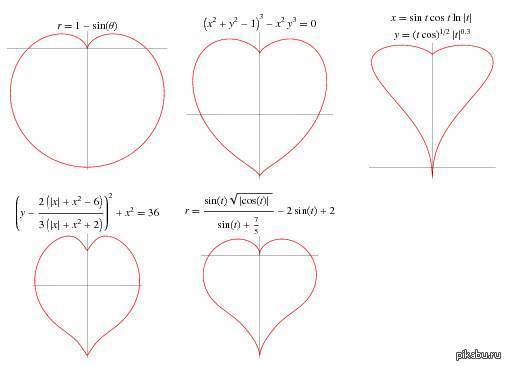График в виде сердца уравнение (5 видео)

График в виде сердца уравнение

Каждый из вас знаком со многими графиками функций: параболой, гиперболой, кубической параболой, но знаете ли вы, что существует такая функция, графиком которой является сердце?

Из уравнения вида ( x 2 + y 2 – 1)3 – x 2 y 3 = 0 получается график в форме сердца.

Давайте попробуем решить его .

Извлечем из кубического корня обе части уравнения:

У нас получилось квадратное уравнение, где a = 1; b = — x 2/3 ; c = x 2 — 1

Находим дискриминант: D = b 2 – 4 ac = (- x 2/3 ) 2 – 4*1*( x 2 -1) = x 4/3 – 4 x 2 + 4 и корни:

Следовательно, на одно значение x приходится два значения y .

Находим несколько значений y , подставляя в функцию значения x :

Содержание

Пусть математика сложит сердца
Дисклеймер
Шаг 1. Параметризуем сердечко.
Шаг 2. От параметрического задания к неявной функции.
Шаг 3. От неявной функции к функции двух переменных. Функция цвета.
Шаг 4. Добавляем параметр, создаём анимацию.
График в виде сердца
Содержание
Уравнения [ править | править код ]
Свойства [ править | править код ]
Обобщение [ править | править код ]
История [ править | править код ]
Дисклеймер
Шаг 1. Параметризуем сердечко.
Шаг 2. От параметрического задания к неявной функции.
Шаг 3. От неявной функции к функции двух переменных. Функция цвета.
Шаг 4. Добавляем параметр, создаём анимацию.
Дубликаты не найдены
📸 Видео

Видео:Что лежит в сердце математика?Скачать

Пусть математика сложит сердца

Один и один — получается два. Все одиноки — здесь ты, а там я.
Люди всегда одиноки вдвойне сами с собою наедине.
Если б их что-то сблизить могло, сразу б из двух получилось одно.
Пусть математика сложит сердца — чтобы проделать нам путь до конца.

Уильямс Джей, «Герои Ниоткуда»

Вероятно, пост следовало назвать «Как нарисовать анимированное сердечко ко дню Святого Валентина, используя математику не по назначению». Я отверг это название в пользу более поэтичного: как-никак, надвигается замечательный романтический праздник, который мы, айтишники и прочие нёрды, должны встретить во всеоружии. Я сразу покажу вам результат, а под хабракатом будет много букв о том, как я этого результата достиг.

Дисклеймер

Я осознаю, что красивое мигающее сердечко можно сделать и без малейшего знания математики. Но разве это интересно?

Шаг 1. Параметризуем сердечко.

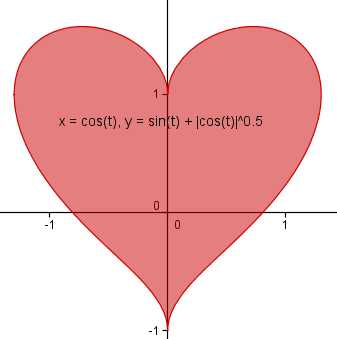
Для начала нам нужен математический объект, хотя бы отдалённо напоминающий сердечко. К счастью, для меня этот шаг был тривиален: ещё пару лет назад я обнаружил замечательную формулу как раз для такого случая (из эстетических соображений график на рисунке растянут по горизонтали, на самом деле он должен умещаться между -1 и 1).

Формула была обнаружена из следующий соображений: возьмём обыкновенную окружность и представим, что она состоит из желе, будучи при этом жёстко прикреплена к оси ординат. Теперь «подуем» на неё снизу: прибавим к координате игрек некую функцию w(x) = w(x(t)), равную нулю при x=0, монотонно возрастающую при x>0 и чётную по x. После такого «дуновения» половинки окружности сместятся вверх, образуя «выпуклости» сердечка, а благодаря жёсткому креплению к оси Y образуется нижний «хвостик» и верхняя «вмятинка». В данном случае w(x(t)) = |x| 1/2 = |cos(t)| 1/2 . Можете самостоятельно попробовать другую «функцию дуновения» и посмотреть, что из этого выйдет.

Шаг 2. От параметрического задания к неявной функции.

x = cos(t)
y = sin(t) + |cos(t)| 1/2
y — |x| 1/2 = sin(t)
(y — |x| 1/2 ) 2 + x 2 = 1
f(x,y) = (y — |x| 1/2 ) 2 + x 2 — 1 = 0

Шаг 3. От неявной функции к функции двух переменных. Функция цвета.

Имея на руках f(x,y), мы наконец можем осуществить свою мечту: нарисовать красивую цветную картинку. Для этого нам понадобится ещё одна функция: функция цвета. Она должна принимать вещественный аргумент r и возвращать целое значение от 0 до 255. Также желательно, чтобы она была монотонна на каждой полуоси и имела максимум в точке нуль. В качестве такой функции можно взять, например, эту:

Здесь 100 — «магическое число», позднее мы его в полном соответствии с «хорошим стилем программирования» заменим параметром.
Теперь для каждой точки (x,y) мы можем задать цвет как rgb(c(f(x,y)), 0, 0). Те точки, которые раньше принадлежали непосредственно графику «сердечка», стали ярко-красными (обратите внимание на неподвижный светлый контур на гифке). По мере удаления от графика цвет будет тускнеть, пока на некотором расстоянии от него не станет чёрным.

Шаг 4. Добавляем параметр, создаём анимацию.

Теперь заменим магическое число 100 параметром k. Новая функция цвета выглядит так:

Пусть k — это некоторая функция времени. Тогда для каждой точки изображения в каждый момент времени мы можем вычислить её цвет (что и является, по сути, математическим определением анимации). Сначала я хотел взять что-нибудь типа k(t) = 80(sin(t)+1). Потом, однако, я понял, что при большом количестве кадров гифка будет весить более 640 килобайт. С другой стороны, при малом количестве кадров нет смысла заморачиваться с аналитическим заданием k(t). В итоге, чтобы добиться пульсирования сердца, я последовательно присвоил k значения 80, 90, 100, 110, 120, 110, 100, 90, а затем изображения, сгенерированные для этих значений, объединил в циклический GIF. В общем-то, всё.

Видео:Математика это не ИсламСкачать

График в виде сердца

Кардио́ида (греч. καρδία — сердце, греч. εἶδος — вид) — плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом [1] . Получила своё название из-за схожести своих очертаний со стилизованным изображением сердца.

Видео:Математическая функция в виде сердцаСкачать

Содержание

Видео:График сердцаСкачать

Уравнения [ править | править код ]

Пусть a — радиусы окружностей, начало координат находится в крайней правой точке горизонтального диаметра неподвижной окружности (см. рисунок). Тогда уравнения кардиоиды можно записать в следующих формах [2] :

В прямоугольных координатах[1] : ( x 2 + y 2 + 2 a x ) 2 − 4 a 2 ( x 2 + y 2 ) = 0 +y^ +2ax)^ -4a^ (x^ +y^ ),=,0>

В прямоугольных координатах (параметрическая запись): x = 2 a cos ⁡ t − a cos ⁡ 2 t y = 2 a sin ⁡ t − a sin ⁡ 2 t

В полярных координатах[2][1] : r = 2 a ( 1 − cos ⁡ φ )

Видео:formula of heart - graph functions #desmos #art #mathСкачать

Свойства [ править | править код ]

Кардиоида является частным случаем улитки Паскаля
Кардиоида является частным случаем синусоидальной спирали
Кардиоида — алгебраическая кривая четвёртого порядка.
Кардиоида имеет один касп.
Длина дуги одного витка кардиоиды, заданной формулой в полярных координатах

r = 2 a ( 1 − cos ⁡ φ ) равна: L = 2 ∫ 0 π r ( φ ) 2 + ( r ′ ( φ ) ) 2 d φ = ⋯ = 8 a ∫ 0 π 1 2 ( 1 − cos ⁡ φ ) d φ = 8 a ∫ 0 π sin ⁡ ( φ 2 ) d φ = 16 a ^

+(r'(varphi ))^ >>;dvarphi =cdots =8aint _ ^

>(1-cos varphi )>>;dvarphi =8aint _ ^

sin( >)dvarphi =16a>

Площадь фигуры, ограниченной кардиоидой, заданной формулой в полярных координатах

r = 2 a ( 1 − cos ⁡ φ ) равна: S = 2 ⋅ 1 2 ∫ 0 π ( r ( φ ) ) 2 d φ = ∫ 0 π 4 a 2 ( 1 − cos ⁡ φ ) 2 d φ = ⋯ = 4 a 2 ⋅ 3 2 π = 6 π a 2 >int _ ^

(1-cos varphi )^ >;dvarphi =cdots =4a^ cdot >pi =6pi a^ >.

Радиус кривизны любой линии:

ρ ( φ ) = [ r ( φ ) 2 + r ˙ ( φ ) 2 ] 3 / 2 r ( φ ) 2 + 2 r ˙ ( φ ) 2 − r ( φ ) r ¨ ( φ ) . + >(varphi )^
ight]^ > +2 >(varphi )^ -r(varphi ) >(varphi )>> .>

Что даёт для кардиоиды заданной уравнением в полярных координатах:

r ( φ ) = 2 a ( 1 − cos ⁡ φ ) = 4 a sin 2 ⁡ φ 2 , >,> ρ ( φ ) = ⋯ = [ 16 a 2 sin 2 ⁡ φ 2 ] 3 2 24 a 2 sin 2 ⁡ φ 2 = 8 3 a sin ⁡ φ 2 . sin ^ >]^ >> sin ^ >>>= >asin > .>

Видео:Как запомнить графики функцийСкачать

Обобщение [ править | править код ]

Кардиоида есть Синусоидальная спираль при n = 1 2

>>;

Кардиоида есть Улитка Паскаля при a = ℓ .

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

История [ править | править код ]

Кардиоида впервые встречается в трудах французского учёного Луи Карре (Louis Carrè, 1705 г.). Название кривой дал в 1741 году Джованни Сальвемини ди Кастиллоне (он упоминается также как Johann Francesco Melchiore Salvemini Castillon).

«Спрямление», то есть вычисление длины кривой, выполнил Ла Ир (Philippe de La Hire), который открыл кривую независимо, в 1708 году. Также независимо описал кардиоиду голландский математик Й. Коерсма (J. Koersma, 1741 год). В дальнейшем к кривой проявляли интерес многие видные математики XVIII—XIX веков.

Один и один — получается два. Все одиноки — здесь ты, а там я.
Люди всегда одиноки вдвойне сами с собою наедине.
Если б их что-то сблизить могло, сразу б из двух получилось одно.
Пусть математика сложит сердца — чтобы проделать нам путь до конца.

Уильямс Джей, «Герои Ниоткуда»

Дисклеймер

Шаг 1. Параметризуем сердечко.

Шаг 2. От параметрического задания к неявной функции.

x = cos(t)
y = sin(t) + |cos(t)| 1/2
y — |x| 1/2 = sin(t)
(y — |x| 1/2 ) 2 + x 2 = 1
f(x,y) = (y — |x| 1/2 ) 2 + x 2 — 1 = 0

Шаг 3. От неявной функции к функции двух переменных. Функция цвета.

Шаг 4. Добавляем параметр, создаём анимацию.

Теперь заменим магическое число 100 параметром k. Новая функция цвета выглядит так:

Дубликаты не найдены

С лекции по анатомии, например.

Поясняю: в норме у человека пульс меняется. Всегда. ЧСС меняется +- несколько ударов в минуту за каждые несколько секунд — поставьте себе постоянный измеритель и поймёте, о чём я. Всего 2 недели назад мерил в течение 2 суток, потому, поверьте, я знаю, о чём я говорю.

В случае инфаркта I-й водитель ритма (в терминологии могу чуть косячить, никогда с ней в ладах не был) отключается, работает II-й (вторичный), который задаёт исключительно ровный пульс, уже не зависящий от состояния организма)
Есть ещё III-й, третичный, водитель ритма (забыл, какая это система), но он не может поддерживать пульс выше 30 ударов в минуту, а потому в случае её работы человек обычно лежит без сознания. Это если отказал II-й, более устойчивый.
III-й же почти неуязвим сам по себе.