Графическое представление уравнения бернулли пьезометрическая и напорная линии (3 видео)

Содержание

Графическое представление и практическое применение уравнения Бернулли
Лекция 4
4.2. Геометрическая интерпретация уравнения Бернулли
4.3. Энергетическая интерпретация уравнения Бернулли
4.4. Уравнение Бернулли для потока реальной жидкости
Дистанционная лабораторная работа 5 по иллюстрации уравнения Бернулли
🎥 Видео

Видео:Уравнение Бернулли гидравликаСкачать

Графическое представление и практическое применение уравнения Бернулли

Диаграмма уравнения Бернулли для потока реальной жидкости показана на рис. 3.4. От центров тяжести сечений / и // отложены отрезки, соответственно равные пьезометрическим высотам и , затем от точек В и В 1 отложены вверх отрезки,соответствующие высотам скоростного напора в этих сечениях

Линия О—О — след плоскости сравнения; линия ВВ’ называется пьезометрической линией; линия СС’ — напорной линией; линия DD’ — линией первоначального напора. Очевидно, отрезок D’C’ соответствует потере напора h_w по длине потока на участке между сечениями / — //.

На основании уравнения Бернулли сконструирован ряд приборов, такие, как , водоструйный насос, эжектор и др.

Графическое представление уравнения бернулли пьезометрическая и напорная линии

Рассмотрим применение уравнения Бернулли на примере водомерного устройства в трубах — водомера Вентури (рис. 3.5), представляющего собой вставку в основную трубу диаметром D трубы меньшего диаметра d, которая соединена с основной трубой коническими переходами. В основной трубе (сечение 1—1) и в суженном сечении (сечение //—//) присоединены пьезометры, по показаниям которых и определим расход жидкости Q в трубе.

Выведем общую формулу водомера для определения расхода жидкости.

Предварительно приняв для заданных условий z₁=z₂=0, a₁=1 и a₂=1 и h_w=0 (ввиду малости расстояния между сечениями), можем записать уравнения Бернулли в виде:

Отсюда следует, что с увеличением скорости движения пьезометрическое давление уменьшается и наоборот. Это положение используется в водомере Вентури, где по разности показаний пьезометров h, зная диаметры D и d, можно определить мгновенный поток.

где и — площади соответствующих сечений

В водоструйном насосе (рис. 3.6) вода из бака 1 поступает в трубу, имеющую сужение. В узком сечении трубы скорость струи возрастает. При этом в соответствии с уравнением Бернулли давление здесь падает ниже атмосферного, благодаря чему происходит подсасывание жидкости по трубке, опущенной в бак 2. При больших скоростях движения жидкость будет подсасываться из бака 2 непрерывно.

Скорость течения движущейся жидкости можно определить трубкой Пито. Этот прибор (рис. 3.7) представляет собой стеклянную трубку, открытую с двух концов. При этом изогнутый под прямым углом конец трубки располагается в жидкости так, чтобы ось нижнего колена совпадала с линией тока. В трубке Пито создается дополнительное давление от воздействия скорости движущейся жидкости (скоростной напор).

Измерение скорости в потоке закрытого трубопровода можно провести по разности показаний трубки Пито , определяющей полный напор h₁=((p/rg)+v 2 /(2g)), и пьезометрической трубки, определяющей пьезометрический напор – h₂=p/rg. Скорость потока (м/с) в точке расположения нижнего отверстия трубки Пито можно определить по высоте подъема жидкости h₃= v 2 /(2g).

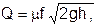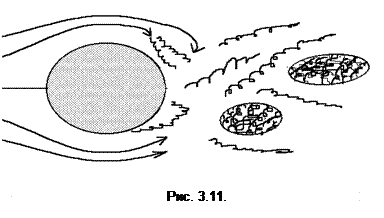
Применяя уравнение Бернулли к случаю истечения жидкости через малое отверстие при постоянном напоре, получаем выражение для расхода жидкости, известное как формула Торричелли:

где m — коэффициент расхода (истечения), который определяется экспериментально и зависит от вида (формы) отверстия; f — площадь поперечного сечения отверстия; h — напор.

Учитывая, что напор h=p/(rg), формулу Торичелли преобразуем к виду

где Δp — перепад давления в отверстии.

Эту формулу часто используют для расчета процессов дросселирования, прохождения жидкости через местное гидравлическое сопротивление (золотники, клапаны и другие гидроаппараты).

3.9. Виды потоков жидкости

Различают два вида течения жидкости в различных условиях: струйное и вихревое. Струйное течение называют ламинарным, а вихревое — турбулентным.

Режим течения оценивается числом Рейнольдса

где v — средняя скорость потока, м/с; n — кинематическая вязкость, м 2 /с; d — гидравлический диаметр; при круглом сечении он соответствует внутреннему диаметру трубы, м; в других случаях его необходимо определять по выражению

Здесь: S — площадь сечения, м 2 ; L — смоченный периметр сечения, м.

Число Рейнольдса — Re является безразмерным. При критическом значении Rе_кр поток переходит из ламинарного режима в турбулентный. Для жестких гладких круглых труб Rе_кр равно 2300, для гибких рукавов 1600, для гладких кольцевых щелей 1000…1100, для окон цилиндрических золотниковых распределителей 260, для кранов 550…750. Критическое значение Rе_кр определяет точку, ниже которой гарантированно не может существовать турбулентный режим течения.

Рассмотрим различные течения жидкости в терминах энергетического спектра и в пространстве состояний, если поместить какое-либо тело в поток жидкости, например, опору моста в русло реки, то при очень малых скоростях жидкость течёт ламинарно (рис.3.8). Такое течение является стационарным, т.е. скорость в любой точке пространства не зависит от времени. Следовательно вся энергия в спектре сосредоточена на нулевой частоте. В пространстве состояний такое течение изображается одной точкой. Эта точка является устойчивой траекторией системы т.е. если начальное течение соответствовало другой точке в пространстве состояний, то в пределе любое распределение скоростей будет стремится к устойчивому. (Строго говоря не любое, а любое из области притяжения устойчивой траектории). С ростом скорости в
потоке образуются вихри, однако картина продолжает оставаться стационарной (рис. 3.9.). Так как поле скоростей по прежнему стационарно, то никаких изменений относительно ламинарного течения в спектре не произойдёт. В пространстве состояний это течение будет так же, как и ламинарное изображаться одной точкой, однако, её положение изменится. При дальнейшем росте скорости возможен отрыв вихрей и их увлечение потоком. Возникает нестационарное течение, которое, например, можно наблюдать с моста. При этом скорость, измеренная в некоторой точке вниз по потоку за мостом, оказывается периодической функцией времени (рис.3.10.). В такой ситуации происходит качественное изменение как энергетического спектра, так и траектории системы в пространстве состояний. В спектре появляется новая частота отличная от нулевой, а траектория в пространстве состояний из точки превращается в устойчивый цикл. В одном из первых сценариев возникновения турбулентности — сценарии Ландау — предполагалось, что по мере увеличения числа Рейнольдса в системе будет возникать всё больше новых частот. Траектория системы будет усложнятся: предельный цикл превратится в двумерный тор, этот тор в свою очередь превратится в трёхмерный и далее бесконечный каскад новых торов. Однако, сейчас не вызывает сомнений, что в большинстве систем сценарий возникновения турбулентности другой и данный сценарий крайне маловероятен. Один из сценариев имеющих экспериментальное подтверждение будет рассмотрен далее. При ещё большем возрастании числа Рейнольдса крупные вихри начинают порождать неупорядоченные внутренние вихри. В зависимости скорости от времени кроме периодической компоненты, появляются так же и нерегулярные отклонения. Спектр
пред

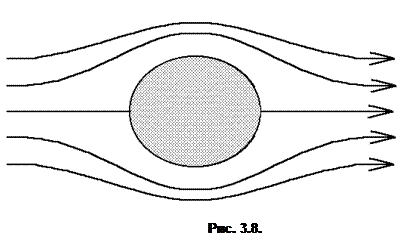
ставляет собой пики основных частот на фоне сравнительно малоинтенсивного «белого шума». Траектория системы начинает размываться. Она совершает нерегулярные колебания небольшой амплитуды около некоторого тора. В этом случае мы наблюдаем следующую картину потока (рис. 3.11.). Если число Рейнольдса возрастёт ещё больше, то возникает чрезвычайно сложное поле скоростей, и траектория системы, становится совершенно хаотической. Непосредственно за телом возникает, так называемый, турблентный след. Из спектра исчезают пики частот и возрастает интенсивность шума. Шум практически равномерно распределён в довольно широком интервале частот. Картина потока соответствующая такой ситуации изображена на рис. 3.12. Полной теории, исчерпывающим образом объясняющей возникновение турбулентности в различных типах гидродинамических течений, на сегодняшний день не существует.

Сопротивление течению жидкости увеличивается, гидравлические потери повышаются.

Потери давления

При протекании по трубопроводу жидкость испытывает сопротивление, зависящее от длины трубы, шероховатости ее внутренних поверхностей, площади и формы поперечного сечения, что вызывает потери давления.

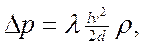В общем случае потери давления в трубах круглого сечения определяют по формуле Дарси-Вейсбаха:

где λ — коэффициент гидравлического трения; l — длина трубы; d — внутренний диаметр трубы.

Для ламинарного течения жидкости коэффициент гидравлического трения

где А может иметь значения от 64 до 150 (например, в идеальном случае при изотермическом потоке А=64; при течение потока в реальных металлических трубах и гибких рукавах А=75…85; при небольшом изгибе рукавов А=108; при изгибе труб более 90° — А = 80; если поток движется по смятой на 40…50 % трубе, то А=150).

Для турбулентного течения коэффициент гидравлического трения

Для определения коэффициентов гидравлического трения разработаны номограммы и таблицы.

Потери давления при ламинарном течении являются линейной функцией скорости (так как в выражении Re содержится скорость), а при турбулентном течении зависят от скорости в степени 1…2.

Кроме потерь давления по длине прямого трубопровода, в гидросистемах имеются потери на местных сопротивлениях: при повороте трубы (рис.3.13, а); при расширении (рис.3.13, б); сужении потока (рис.3.13, в); перекрытии труб аппаратурой управления и регулирования.

Потери давления (Па) на местном сопротивлении

где x — коэффициент местного сопротивления; b — поправочный коэффициент.

Как правило, коэффициенты местных сопротивлений определяются экспериментальным путем и приводятся в справочниках. Например, для штуцеров x = 0,1; при повороте потока на 90° x =2; для гидроаппаратуры x = 1,0. ..4,0.

Поправочный коэффициент b учитывает зависимость потерь от числа Re при ламинарном течении. При Re >2300 b = 1, при Re = 400 b=2, при Re=100 b = 8, при Rе = 10 b = 80. Для нахождения суммарных потерь от местных сопротивлений отдельные коэффициенты x складывают.

Гидравлический удар

Если при течении жидкости в трубопроводе быстро закрыть проходное сечение с помощью задвижки или другого аппарата, то произойдет резкое повышение давления, называемое гидравлическим ударом. При этом кинетическая энергия движущегося потока жидкости перейдет в потенциальную энергию, и давление может во много раз превысить нормальное значение.

Повышение давления вычисляется по уравнению Н. Е. Жуковского:

где с – скорость распространения ударной волны, м/с (для жестких стенок трубы равна скорости звука в жидкости); v – начальная скорость жидкости в трубе (до момента перекрытия сечения), м/с.

Гидравлический удар может возникать во всех случаях быстрого перерыва подачи жидкости. Чтобы уменьшить вероятность его возникновения, увеличивают время закрытия задвижки (крана), при возможности уменьшают длину трубы, присоединяют к трубе дополнительные емкости в виде компенсаторов, гидроаккумуляторов.

При упругих стенках трубы скорость распространения ударной волны

где d — внутренний диаметр трубы, м; d — толщина стенок трубы, м; Ε_ж и Ε_тр — модули упругости жидкости и материала трубы, Па.

Кавитация

При движении жидкости в сужающейся трубе, типа трубки Вентури, в наиболее узком сечении ее скорость достигает наибольшего значения, а давление будет минимальным. Предел уменьшения величины давления зависит прежде всего от того, что течет по трубопроводу: газ или капельная жидкость.

Кипение капельной жидкости (вода, спирт, масло и др.) при заданной температуре может быть получено понижением давления. Давление, при котором происходит кипение жидкости, называется давлением парообразования р_к.

Величину давления парообразования р_к для различных жидкостей можно найти в физических справочниках. В качестве примера приведем величину р_к для воды:

t, °C . 200 100 40 20 4

р_к, мм. рт. Cm.. 11660 760 55,3 17 4

Из приведенных данных видно, что при температуре 20° С вода закипает при давлении 17 мм рт. ст. Если давление в наиболее узком сечении трубопровода достигнет давления парообразования, то жидкость в этом месте начнет кипеть и в трубе при этом образуются полости, заполненные паром, — каверны.

Закипание жидкости при пониженном давлении, возникающем в результате возрастания скорости потока, и образование в текущей жидкости полостей, заполненных паром или газом приводит к кавитации.

Кавитация может происходить во всех капельных жидкостях, в том числе и в жидких металлах. Последнее иногда наблюдается при использовании жидких металлов в качестве теплоносителей на атомных электростанциях.

Если после наиболее узкого сечения, в котором происходит кавитация, последует расширение трубы, то основная масса жидкости на этом участке будет двигаться в виде свободной струи, окруженной пенообразной смесью пузырьков пара и жидкости. Далее, ниже по течению, в некоторой точке паровая зона замкнется на стенке, и поток жидкости заполнит все сечение трубы.

Кавитация возникает не только при движении жидкости в трубопроводах, но и при внешнем обтекании тел, в частности, на ло-пастях гребных винтов, рабочих колес гидравлических турбин и насосов. Желательное увеличение скоростей вращения рабочих колес насосов, гидравлических турбин приводит к тому, что скорости становятся настолько большими, что в некоторой области давление падает до давления парообразования, и возникает кавитация.

Появление кавитации всегда вызывает увеличение сопротивления, т, е. добавочную потерю энергии. Кроме этого, она приводит к разрушению металла и появлению кавитационных шумов. Последствия кавитации настолько существенны, что обычно при проектировании насосов, турбин и винтов лопасти рассчитывают так, чтобы на них не возникала кавитация.

В качестве критерия, определяющего кавитационные свойства профилей, применяют число кавитации

где р и V — соответственно давление и скорость в набегающем потоке.

Улучшение кавитационных свойств лопастей, т. е. уменьшение кавитационного числа, является одной из важнейших задач конструкторских бюро по проектированию насосов, турбин и винтов. Очевидно, что на лопастях кавитация возникает в точках, где давление наименьшее, а следовательно, скорость наибольшая. На рис. 3.14, а показана область возникновения кавитации на профиле крыла [5]. Кавитационная коррозия металла обычно происходит в местах, где кавитационная каверна замыкается. Природа разрушения металла еще недостаточно изучена, но можно утверждать, что разрушение происходит под действием очень мощных механических ударов пузырьков пара и жидкости, химического воздействия богатого кислородом воздуха, содержащегося в воде, и, как утверждают некоторые авторы, электрических полей, возникающих в каверне.

В результате всего этого воздействия почти все металлы разъедаются, их поверхность приобретает губчатый вид, и лопасти ломаются. Иногда процесс разрушения и поломки лопастей происходит очень быстро.

Шумы, возникающие при появлении кавитации, настолько велики, что они могут служить причиной вибрации отдельных элементов машин, приводящих к неустойчивой работе их и даже разрушению.

На рис. 3.14, б показан так называемый суперкавитирующий профиль лопатки корабельного винта. У таких винтов область кавитации не замыкается на поверхности лопасти, а уходит в бесконечность. Поэтому они не подвергаются интенсивной кави-тационной коррозии. Суперкавитирующие винты применяются на некоторых быстроходных судах.

Если нарушается сплошность потока жидкости, то возникает кавитация. Дело в том, что испарение жидкости происходит как непосредственно с ее поверхности, так и путем образования во всем ее объеме пара в виде пузырьков, которые затем разрушаются (конденсируются) при попадании в зону повышенного давления. Это вызывает появление микропустот, т. е. нарушение сплошности жидкости.

Таким образом, кавитация – это свойство движущейся жидкости образовывать паровоздушные пузыри с последующим их разрушением.

Кавитация часто возникает во всасывающих гидролиниях в результате местного уменьшения давления ниже критического значения (оно приблизительно равно давлению насыщенного пара этой жидкости при данной температуре). Она сопровождается гидравлическими микроударами и, как следствие, большим местным повышением температуры и давления, что вызывает разрушение деталей, появление вибраций, снижение КПД и др.

С кавитацией борются также, уменьшая разрежение в зонах ее возможного появления, в частности путем повышения давления. При этом применяют подпор во всасывающей линии насоса, а также эластичные специальные разделители сред в баках насосных установок. Используют материалы, стойкие против кавитационного разрушения, – бронзу, титан, коррозионно-стойкую сталь, повышая чистоту их обработки.

1. Понятие потока, единицы измерения.

2. Виды потоков жидкости. Отметьте особенности потоков.

3. Критерий Рейнольдса.

4. Закон неразрывности потока, его смысл.

5. Уравнение Бернулли. Составляющие данного уравнения.

6. Приборы, основанные на применении уравнения Бернулли. Отметьте их особенности..

7. Гидравлический удар. Уравнение Жуковского Н.Е.

8. Меры предотвращения гидравлического удара.

9. Нарисуйте возможную схему использования дополнительных элементов для предотвращения гидроудара во всасывающей линии гидронасоса.

10. Укажите возможность использования явления гидравлического удара.

11. Определение потерь давления, определяемых длиной трубопровода. Формула Дарси-Вейсбаха.

12. Особенности определения потерь давления в местных сопротивлениях.

13. Определение потерь давления в реальной гидросистеме.

14. Кавитация. Особенности, методы предотвращения кавитации.

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Лекция 4

4.1. Уравнение Бернулли для жидкости

Рассмотрим поток жидкости, проходящий по трубопроводу переменного сечения (рис. 10). В первом сечении гидродинамический напор пусть равен H1. По ходу движения потока часть напора H1 необратимо потеряется из-за проявления сил внутреннего трения жидкости и во втором сечении напор уменьшится до H2 на величину потерь напора H.

Уравнение Бeрнýлли для жидкости в самом простейшем виде записывается так:

то есть это уравнение для двух сечений потока в направлении его течения, выраженное через гидродинамические напоры и отражающее закон сохранения энергии (часть энергии переходит в потери) при движении жидкости.

Уравнение Бeрнýлли в традиционной записи получим, если в последнем равенстве раскроем значения гидродинамических напоров H1 и H2 (м) :

Энергетический смысл уравнения Бeрнулли заключается в том, что оно отражает закон сохранения энергии: сумма потенциальной z+hp, кинетической v2/2g энергии и энергии потерь H остаётся неизменной во всех точках потока.

4.2. Геометрическая интерпретация уравнения Бернулли

Положение любой частицы жидкости относительно некоторой произвольной линии нулевого уровня 0-0 определяется вертикальной координатой Z. Для реальных гидравлических систем это может быть уровень, ниже которого жидкость из данной гидросистемы вытечь не может. Например, уровень пола цеха для станка или уровень подвала дома для домашнего водопровода.

· Как и в гидростатике, величину Z называют нивелирной высотой.

· Второе слагаемое — носит название пьезометрическая высота. Эта величина соответствует высоте, на которую поднимется жидкость в пьезометре, если его установить в рассматриваемом сечении, под действием давления P.

· Сумма первых двух членов уравнения ¾ гидростатический напор.

· Третье слагаемое в уравнения Бернулли называется скоростной высотой или скоростным напором. Данную величину можно представить как высоту, на которую поднимется жидкость, начавшая двигаться вертикально со скорость u при отсутствии сопротивления движению.

· Сумму всех трёх членов (высот) называют гидродинамическим или полным напором и, как уже было сказано, обозначают буквой Н.

Все слагаемые уравнения Бернулли имеют размерность длины и их можно изобразить графически.

4.3. Энергетическая интерпретация уравнения Бернулли

Выше было получено уравнение Бернулли с использованием энергетических характеристик жидкости. Суммарной энергетической характеристикой жидкости является её гидродинамический напор.

С физической точки зрения это отношение величины механической энергии к величине веса жидкости, которая этой энергией обладает. Таким образом, гидродинамический напор нужно понимать как энергию единицы веса жидкости. И для идеальной жидкости эта величина постоянна по длине. Таким образом, физический смысл уравнения Бернулли это закон сохранения энергии для движущейся жидкости.

Физический смысл слагаемых, входящих в уравнение следующий:

· Z — потенциальная энергия единицы веса жидкости (удельная энергия) – энергия, обусловленная положением (высотой) единицы веса жидкости относительно плоскости сравнения (нулевого уровня), принимаемой за начало отсчета;

· — потенциальная энергия единицы веса жидкости — энергия, обусловленная степенью сжатия единицы веса жидкости, находящейся под давлением ;

· — полная потенциальная энергия единицы веса жидкости;

· — кинетическая энергия единицы веса жидкости — энергия, обусловленная движением единицы веса жидкости со скоростью u;

· H — полная энергия единицы веса жидкости (полная удельная энергия).

4.4. Уравнение Бернулли для потока реальной жидкости

В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т. е. напор потока Hпотока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора Δh составят:

где H1-1— напор в первом сечении потока жидкости,

H2-2 — напор во втором сечении потока,

∆h — потерянный напор — энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.

С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть

Индексами 1 и 2 обозначены характеристики потока в сечениях 1-1 и 2-2.

Если учесть, что характеристики потока V и α зависят от геометрии потока, которая для напорных потоков определяется геометрией трубопровода, понятно, что потери энергии (напора) в разных трубопроводах будут изменяться неодинаково. Показателем изменения напора потока является гидравлический уклон I, который характеризует потери напора на единице длины потока. Физический смысл гидравлического уклона – интенсивность рассеяния энергии по длине потока. Другими словами, величина I показывает, как быстро трубопровод поглощает энергию потока, протекающего в нём

Изменение энергии по длине потока удобно проследить на графиках. Из уравнения Бернулли для потока реальной жидкости (закона сохранения энергии) видно, что гидродинамическая линия для потока реальной жидкости (с одним источником энергии) всегда ниспадающая. То же справедливо и для пьезометрической линии, но только в случае равномерного движения, когда скоростной напор а уменьшение напора происходит только за счёт изменения потенциальной энергии потока, главным образом за счёт уменьшения давления P.

4.5. Разность напоров и потери напора

Различие в применении терминов «разность напоров» и «потери напора» с одним и тем же обозначениемH поясним на примерах.

Движение жидкости происходит только при наличии разности напоров (H = H1 — H2), от точки с бóльшим напором H1 к точке с меньшим H2. Например, если два бака, заполненных водой до разных высотных отметок, соединить трубопроводом, то по нему начнётся перетекание в бак с меньшей отметкой уровня воды под влиянием разности напоров H, равной в этом случае разности отметок уровней воды в баках. При выравнивании уровней напоры в обоих баках становятся одинаковыми H1 = H2 , разность напоров H=0 и перетекание прекращается.

Потери напора H отражают потерю полной энергии потока при движении жидкости. Если в предыдущем примере на трубе установить задвижку и закрыть её, то движение воды прекратится и потерь напора не будет (H = = 0), однако разность уровней воды будет создавать некоторую разность напоров H. После открывания задвижки вода вновь начнёт перетекать по трубе и общие потери напора в трубопроводе при движении из одного бака в другой будут равны разности напоров в баках H = H1 — H2 , то есть мы опять пришли к уравнению Бернулли.

Таким образом, «разность напоров» является причиной движения воды, а «потеря напора» — следствием. При установившемся движении жидкости они равны. Измеряются они в одних и тех же единицах СИ: метрах по высоте.

Обычно в гидравлических задачах при известных v или q определяемая величина H назывется потерей напора и, наоборот, при определении v или q известная H — разностью напоров.

4.6. Связь давления и скорости в потоке

Связь давления и скорости в потоке жидкости — обратная: если в каком-то месте потока скорость увеличивается, то давление здесь малó, и, наоборот, там, где скорости невелики, давление повышенное. Эту закономерность объясним на основе уравнения Бернýлли.

Рассмотрим работу водоструйного насоса (см. рис. 11). На подходе по нагнетательному трубопроводу 1 поток рабочей жидкости имеет относительно небольшую скорость v1 и высокое избыточное давление pизб1. Проходя через соплó 2, поток сужается, скорость его резко возрастает до v2. Для дальнейших рассуждений запишем уравнение Бернýлли так:

Здесь нет z1 и z2, так как труба горизонтальная, а величиной потерь напора DH» 0 пренебрегаем. Так как в правой части уравнения кинетическая составляющая энергии потока резко возросла из-за увеличения v2, то потенциальная составляющая, связанная с избыточным давлением после соплá pизб2, наоборот, уменьшится. Величину pизб2 можно выразить из этого уравнения и найти численное значение. Если pизб2 получается отрицательным, то, значит, возник вакуум (полное давление в струе стало меньше атмосферного). В последнем случае пьезометрическая линия опустится ниже отметки самой струи (см. рис 11).

Таким образом в струе рабочей жидкости после соплá образуется область пониженного давления или даже вакуум, что вызывает подсос транспортируемой жидкости по всасывающему трубопроводу 3 (см. рис. 11). Далее обе жидкости смешиваются в горловине 4 и транспортируются по отводящему трубопроводу 5.

Водоструйные насосы не имеют трущихся частей, в этом их преимущество перед механическими. По их принципу работают также эжекторы, гидроэлеваторы, насосы для создания вакуума.

Видео:Закон БернуллиСкачать

Дистанционная лабораторная работа 5 по иллюстрации уравнения Бернулли

Цель работы. Опытное подтверждение уравнения Д. Бернулли, т. е. понижения механической энергии по течению и перехода потенциальной энергии в кинетическую и обратно (связи давления со скоростью).

Задание. На основе замеров при просмотре фильма и анализе фотографии течения жидкости в канале переменного сечения в устройстве № 4 построить линии энергий для потока и проверить их соответствие уравнению Бернулли.

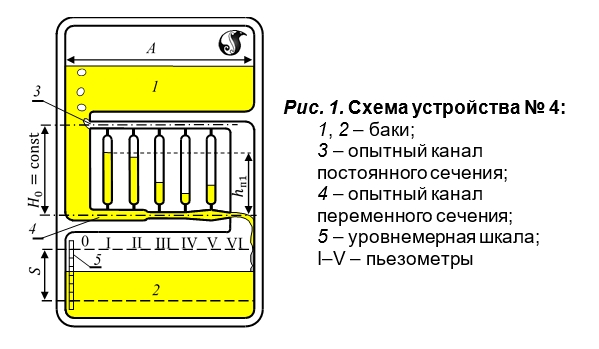
Описание устройства № 4. Устройство № 4 содержит баки 1 и 2, сообщаемые через опытные каналы постоянного 3 и переменного 4 сечений (рис. 1). Каналы соединены между собой равномерно расположенными пьезометрами I–V, служащими для измерения пьезометрических напоров в характерных сечениях. Устройство заполнено подкрашенной водой.

В одном из баков предусмотрена шкала 5 для измерения уровня воды. При перевертывании устройства, благодаря постоянству напора истечения Н о во времени, обеспечивается установившееся движение воды в нижнем канале. Другой канал в это время пропускает воздух, вытесняемый жидкостью из нижнего бака в верхний.

Порядок выполнения работы.

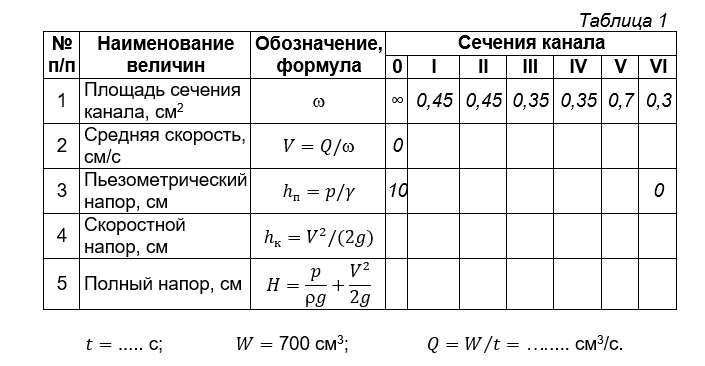
1. Зарисовать схему устройства № 4 и составить таблицу следующего вида.

2. Посмотреть фильм с демонстрацией течения воды через канал переменного сечения в устройстве № 4 и секундомером замерить время t полного опорожнения верхнего бака.

3. Под таблицей записать значение времени t t опорожнения бака, объем бака принять равным W=700 см 3 и определить расход Q=W/t Q = W t .

4. В строке (стр.) 2 рассчитать среднюю скорость течения жидкости в каждом сечении канала: V=Q / w ω Скорость в нулевом сечении (перед входом в канал) принять равной нулю.

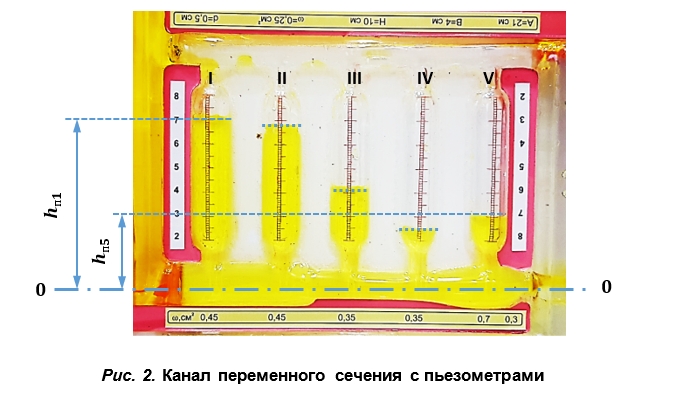
5. На фотографии канала с пьезометрами (рис. 2) снять показания пьезометров h_П1 . . . . h_П5 и записать их в стр. 3. В сечении VI пьезометрический напор равен 0.

6. В стр. 4 определить скоростной напор h_к в сечениях канала. Принять g = 981 см/с 2 .

7. В стр. 5 определить полный напор H H (полную удельную энергию) в каждом сечении. Так как опытный канал горизонтальный и плоскость сравнения 0–0 проведена через его ось, то геометрический напор z₁= z₂= 0 .

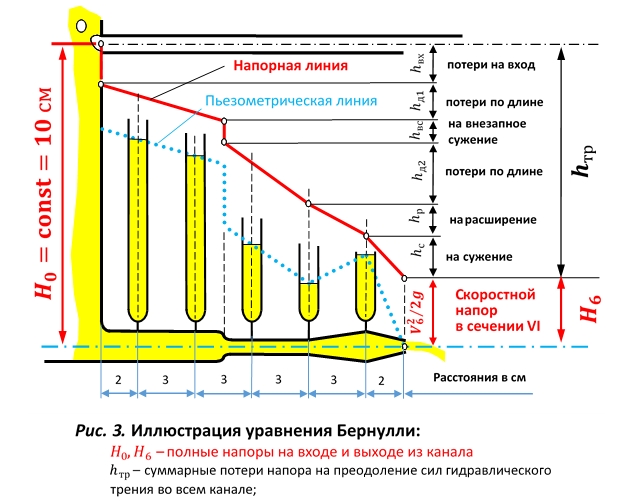
8. Вычертить в масштабе канал с осями пьезометров (рис. 3). Отложить от оси канала пьезометрические напоры h_П h _п на осях пьезометров, наметить уровни жидкости и соединить их между собой и центром выходного сечения VI , как показано на рис. 3. Получится пьезометрическая линия, показывающая изменение потенциальной энергии (давления) вдоль потока. Для получения напорной линии (линии полной механической энергии) нужно отложить от оси канала полные напоры Н и соединить полученные точки, как показано на рис. 3.

9. Проанализировать изменения полной механической H , потенциальной 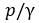и кинетической V 2 /(2g) V 2 /(2 g ) энергий жидкости вдоль потока и проверить их соответствие нижеприведенным правилам построения линий энергий, вытекающим из уравнения Бернулли.

А. Напорная линия (полный напор 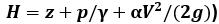постоянно понижается по течению (если на рассматриваемом участке нет насоса) ввиду необратимого преобразования механической энергии в тепловую при преодолении потоком сил гидравлического трения. Причем уклон линии (потери напора h тр ) тем больше, чем меньше сечение участка потока (см. рис. 3).

Б. Пьезометрическая линия отражает изменение потенциальной энергии (z + 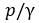) , и, в отличие от напорной, может не только понижаться, но и повышаться по течению. Это происходит при расширении потока (см. рис. 2, 3) за счет повышения давления p ввиду уменьшения скорости V . Пьезометрическая линия проходит через центр тяжести выходного сечения канала (трубопровода) при истечении жидкости в атмосферу и ниже оси канала, если давление в нем меньше атмосферного.

В. Расстояние между пьезометрической и напорной линиями численно равно кинетической энергии 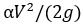α V 2 /( 2 g ) и поэтому обратно пропорционально диаметру трубы. Для участков потоков постоянного сечения средние скорости одинаковы по пути, поэтому такие линии, как правило, параллельны между собой (рис. 3). Эти линии для потоков в конфузорах (конических сходящихся патрубках) расходятся, а в диффузорах (конических расходящихся патрубках) – сходятся. В баках и водоёмах, где жидкость не движется (V=0) ( V =0) , напорная и пьезометрическая линии энергий совпадают со свободной поверхностью, если она находится под атмосферным давлением.

10. Записать выводы , где указать какие знания и навыки получены при выполнении данной работы и в каких сферах инженерной деятельности они могут быть применены.