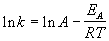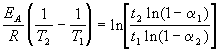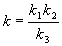Графическое и аналитическое решение уравнения аррениуса

Из качественных соображений понятно, что скорость реакций должна увеличиваться с ростом температуры, т.к. при этом возрастает энергия сталкивающихся частиц и повышается вероятность того, что при столкновении произойдет химическое превращение. Для количественного описания температурных эффектов в химической кинетике используют два основных соотношения — правило Вант-Гоффа и уравнение Аррениуса.

Правило Вант-Гоффа заключается в том, что при нагревании на 10 о С скорость большинства химических реакций увеличивается в 2 4 раза. Математически это означает, что скорость реакции зависит от температуры степенным образом:

, (4.1)

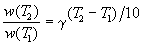
где — температурный коэффициент скорости ( = 24). Правило Вант-Гоффа является весьма грубым и применимо только в очень ограниченном интервале температур.

Гораздо более точным является уравнение Аррениуса, описывающее температурную зависимость константы скорости:

, (4.2)

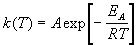
где R — универсальная газовая постоянная; A — предэкспоненциальный множитель, который не зависит от температуры, а определяется только видом реакции; E_A — энергия активации, которую можно охарактеризовать как некоторую пороговую энергию: грубо говоря, если энергия сталкивающихся частиц меньше E_A, то при столкновении реакция не произойдет, если энергия превышает E_A, реакция произойдет. Энергия активации не зависит от температуры.

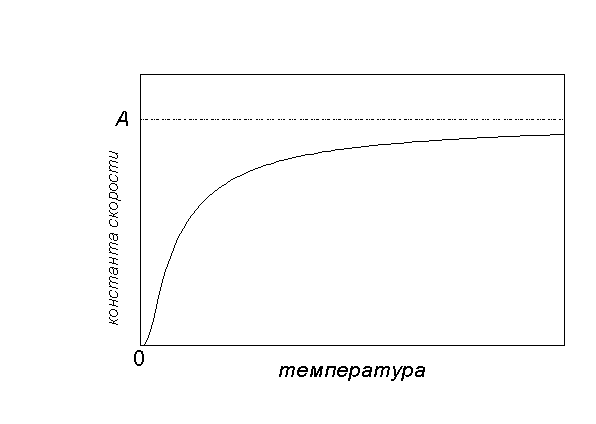
Графически зависимость k(T) выглядит следующим образом:

При низких температурах химические реакции почти не протекают: k(T) 0. При очень высоких температурах константа скорости стремится к предельному значению: k(T) A. Это соответствует тому, что все молекулы являются химически активными и каждое столкновение приводит к реакции.

Энергию активации можно определить, измерив константу скорости при двух температурах. Из уравнения (4.2) следует:

. (4.3)

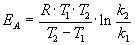
Более точно энергию активации определяют по значениям константы скорости при нескольких температурах. Для этого уравнение Аррениуса (4.2) записывают в логарифмической форме

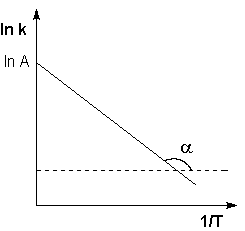
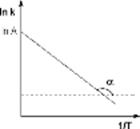
и записывают экспериментальные данные в координатах ln k — 1/T. Тангенс угла наклона полученной прямой равен —E_A / R.

Для некоторых реакций предэкспоненциальный множитель слабо зависит от температуры. В этом случае определяют так называемую опытную энергию активации:

. (4.4)

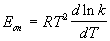
Если предэкспоненциальный множитель — постоянный, то опытная энергия активации равна аррениусовской энергии активации: E_оп = E_A.

Пример 4-1. Пользуясь уравнением Аррениуса, оцените, при каких температурах и энергиях активации справедливо правило Вант-Гоффа.

Решение. Представим правило Вант-Гоффа (4.1) как степенную зависимость константы скорости:

,

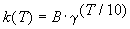
где B — постоянная величина. Сравним это выражение с уравнением Аррениуса (4.2), приняв для температурного коэффициента скорости значение

.

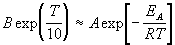
Возьмем натуральный логарифм обеих частей этого приближенного равенства:

.

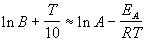
Продифференцировав полученное соотношение по температуре, найдем искомую связь связь между энергией активации и температурой:

.

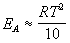
Если энергия активации и температура примерно удовлетворяют этому соотношению, то правилом Вант-Гоффа для оценки влияния температуры на скорость реакции пользоваться можно.

Пример 4-2. Реакция первого порядка при температуре 70 о С завершается на 40% за 60 мин. При какой температуре реакция завершится на 80% за 120 мин, если энергия активации равна 60 кДж/моль?

Решение. Для реакции первого порядка константа скорости выражается через степень превращения следующим образом:

,

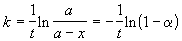
где a = x/a — степень превращения. Запишем это уравнение при двух температурах с учетом уравнения Аррениуса:

,

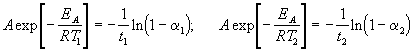
где E_A = 60 кДж/моль, T₁ = 343 K, t₁ = 60 мин, a ₁ = 0.4, t₂ = 120 мин, a ₂ = 0.8. Поделим одно уравнение на другое и прологарифмируем:

Подставляя в это выражение приведенные выше величины, находим T₂ = 333 К = 60 о С.

Пример 4-3. Скорость бактериального гидролиза мышц рыб удваивается при переходе от температуры -1.1 о С к температуре +2.2 о С. Оцените энергию активации этой реакции.

Решение. Увеличение скорости гидролиза в 2 раза обусловлено увеличением константы скорости: k₂ = 2k₁. Энергию активации по отношению констант скорости при двух температурах можно определить из уравнения (4.3) с T₁ = t₁ + 273.15 = 272.05 K, T₂ = t₂ + 273.15 = 275.35 K:

130800 Дж/моль = 130.8 кДж/моль.

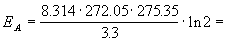
4-1. При помощи правила Вант-Гоффа вычислите, при какой температуре реакция закончится через 15 мин, если при 20 о С на это требуется 2 ч. Температурный коэффициент скорости равен 3.(ответ)

4-2. Время полураспада вещества при 323 К равно 100 мин, а при 353 К — 15 мин. Определите температурный коэффициент скорости.(ответ)

4-3. Какой должна быть энергия активации, чтобы скорость реакции увеличивалась в 3 раза при возрастании температуры на 10 0 С а) при 300 К; б) при 1000 К?(ответ)

4-4. Реакция первого порядка имеет энергию активации 25 ккал/моль и предэкспоненциальный множитель 5 . 10 13 сек -1 . При какой температуре время полураспада для данной реакции составит: а) 1 мин; б) 30 дней?(ответ)

4-5. В каком из двух случаев константа скорости реакции увеличивается в большее число раз: при нагревании от 0 о С до 10 о С или при нагревании от 10 о С до 20 о С? Ответ обоснуйте с помощью уравнения Аррениуса.(ответ)

4-6. Энергия активации некоторой реакции в 1.5 раза больше, чем энергия активации другой реакции. При нагревании от T₁ до T₂ константа скорости второй реакции увеличилась в a раз. Во сколько раз увеличилась константа скорости первой реакции при нагревании от T₁ до T₂?(ответ)

4-7. Константа скорости сложной реакции выражается через константы скорости элементарных стадий следующим образом:

Выразите энергию активации и предэкспоненциальный множитель сложной реакции через соответствующие величины, относящиеся к элементарным стадиям.(ответ)

4-8. В необратимой реакции 1-го порядка за 20 мин при 125 о С степень превращения исходного вещества составила 60%, а при 145 o C такая же степень превращения была достигнута за 5.5 мин. Найдите константы скорости и энергию активации данной реакции .(ответ)

4-9. Реакция 1-го порядка при температуре 25 о С завершается на 30% за 30 мин. При какой температуре реакция завершится на 60% за 40 мин, если энергия активации равна 30 кДж/моль?(ответ)

4-10. Реакция 1-го порядка при температуре 25 о С завершается на 70% за 15 мин. При какой температуре реакция завершится на 50% за 15 мин, если энергия активации равна 50 кДж/моль?(ответ)

4-11. Константа скорости реакции первого порядка равна 4.02 . 10 -4 с -1 при 393 К и 1.98 . 10 -3 с -1 при 413 К. Рассчитайте предэкспоненциальный множитель для этой реакции.(ответ)

4-12. Для реакции H₂ + I₂ 2HI константа скорости при температуре 683 К равна 0,0659 л/(моль. мин), а при температуре 716 К — 0,375 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 700 К.(ответ)

4-13. Для реакции 2N₂O 2N₂ + O₂ константа скорости при температуре 986 К равна 6,72 л/(моль. мин), а при температуре 1165 К — 977,0 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 1053,0 К.(ответ)

4-14. Трихлорацетат-ион в ионизирующих растворителях, содержащих H + , разлагается по уравнению

H + + CCl₃COO — CO₂ + CHCl₃

Стадией, определяющей скорость реакции, является мономолекулярный разрыв связи C- C в трихлорацетат-ионе. Реакция протекает по первому порядку, и константы скорости имеют следующие значения: k = 3.11 . 10 -4 с -1 при 90 о С, k = 7.62 . 10 -5 с -1 при 80 о С. Рассчитайте а) энергию активации, б) константу скорости при 60 о С.(ответ)

4-15. Для реакции CH₃COOC₂H₅ + NaOH ѕ CH₃COONa + C₂H₅OH константа скорости при температуре 282,6 К равна 2,307 л/(моль. мин), а при температуре 318,1 К — 21,65 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 343 К.(ответ)

4-16. Для реакции C₁₂H₂₂O₁₁ + H₂O C₆H₁₂O₆ + C₆H₁₂O₆ константа скорости при температуре 298,2 К равна 0,765 л/(моль. мин), а при температуре 328,2 К — 35,5 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 313,2 К.(ответ)

4-17. Вещество разлагается двумя параллельными путями с константами скорости k₁ и k₂. Какова разность энергий активации этих двух реакций, если при 10 o C k₁/k₂ = 10, а при 40 o C k₁/k₂ = 0.1?(ответ)

4-18. В двух реакциях одинакового порядка разница энергий активации составляет E₂ — E₁ = 40 кДж/моль. При температуре 293 К отношение констант скорости равно k₁/k₂ = 2. При какой температуре константы скорости сравняются?(ответ)

4-19. Разложение ацетондикарбоновой кислоты в водном растворе — реакция первого порядка. Измерены константы скорости этой реакции при разных температурах:

T, о С

k. 10 5 , с -1

Рассчитайте энергию активации и предэкспоненциальный множитель. Чему равен период полураспада при 25 о С? (ответ)

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

Видео:Использование уравнения Аррениуса для решения задач (2/2). Химия для поступающих.Скачать

Графическое и аналитическое решение уравнения аррениуса

ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ

Конспект лекций для студентов биофака ЮФУ (РГУ)

2.1 СКОРОСТЬ ХИМИЧЕСКОЙ РЕАКЦИИ

2.1.9 Влияние температуры на константу скорости реакции

Константа скорости реакции есть функция от температуры; повышение температуры, как правило, увеличивает константу скорости. Первая попытка учесть влияние температуры была сделана Я. Г. Вант-Гоффом, который сформулировал следующее эмпирическое правило:

При повышении температуры на каждые 10 градусов константа скорости элементарной химической реакции увеличивается в 2 – 4 раза.

Величина, показывающая, во сколько раз увеличивается константа скорости при повышении температуры на 10 градусов, есть температурный коэффициент константы скорости реакции γ . Математически правило Вант-Гоффа можно записать следующим образом:

(II.29)

(II.30)

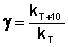
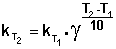
Однако правило Вант-Гоффа применимо лишь в узком температурном интервале, поскольку температурный коэффициент скорости реакции γ сам является функцией от температуры; при очень высоких и очень низких температурах γ становится равным единице (т.е. скорость химической реакции перестает зависеть от температуры).

2.1.10 Уравнение Аррениуса

Очевидно, что взаимодействие частиц осуществляется при их столкновениях; однако число столкновений молекул очень велико и, если бы каждое столкновение приводило к химическому взаимодействию частиц, все реакции протекали бы практически мгновенно. С. Аррениус постулировал, что столкновения молекул будут эффективны (т.е. будут приводить к реакции) только в том случае, если сталкивающиеся молекулы обладают некоторым запасом энергии – энергией активации.

Энергия активации есть минимальная энергия, которой должны обладать молекулы, чтобы их столкновение могло привести к химическому взаимодействию.

Рассмотрим путь некоторой элементарной реакции

Поскольку химическое взаимодействие частиц связано с разрывом старых химических связей и образованием новых, считается, что всякая элементарная реакция проходит через образование некоторого неустойчивого промежуточного соединения, называемого активированным комплексом:

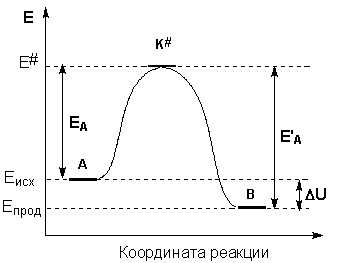
Образование активированного комплекса всегда требует затраты некоторого количества энергии, что вызвано, во-первых, отталкиванием электронных оболочек и атомных ядер при сближении частиц и, во-вторых, необходимостью построения определенной пространственной конфигурации атомов в активированном комплексе и перераспределения электронной плотности. Таким образом, по пути из начального состояния в конечное система должна преодолеть своего рода энергетический барьер. Энергия активации реакции приближённо равна превышению средней энергии активированного комплекса над средним уровнем энергии реагентов. Очевидно, что если прямая реакция является экзотермической, то энергия активации обратной реакции Е’_А выше, нежели энергия активации прямой реакции E_A. Энергии активации прямой и обратной реакции связаны друг с другом через изменение внутренней энергии в ходе реакции. Вышесказанное можно проиллюстрировать с помощью энергетической диаграммы химической реакции (рис. 2.5).

Рис. 2.5 Энергетическая диаграмма химической реакции.
E_исх – средняя энергия частиц исходных веществ,
E_прод – средняя энергия частиц продуктов реакции

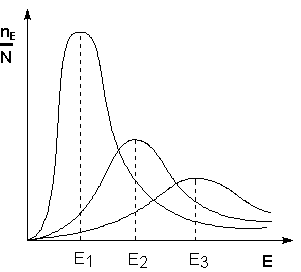
Поскольку температура есть мера средней кинетической энергии частиц, повышение температуры приводит к увеличению доли частиц, энергия которых равна или больше энергии активации, что приводит к увеличению константы скорости реакции (рис.2.6):

Рис. 2.6 Распределение частиц по энергии
Здесь nЕ/N – доля частиц, обладающих энергией E;
E_i — средняя энергия частиц при температуре T_i (T₁ уравнения Аррениуса . Согласно уравнению изобары Вант-Гоффа,

(II.31)

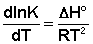
Поскольку константа равновесия есть отношение констант скоростей прямой и обратной реакции, можно переписать выражение (II.31) следующим образом:

(II.32)

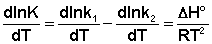
Представив изменение энтальпии реакции ΔHº в виде разности двух величин E₁ и E₂, получаем:

(II.33)

(II.34)

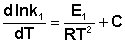
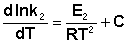
Здесь С – некоторая константа. Постулировав, что С = 0, получаем уравнение Аррениуса, где E_A – энергия активации :

(II.35)

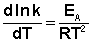
После неопределенного интегрирования выражения (II.35) получим уравнение Аррениуса в интегральной форме:

(II.36)

(II.37)

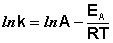
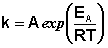
Рис. 2.7 Зависимость логарифма константы скорости химической
реакции от обратной температуры.

Здесь A – постоянная интегрирования. Из уравнения (II.37) нетрудно показать физический смысл предэкспоненциального множителя A, который равен константе скорости реакции при температуре, стремящейся к бесконечности. Как видно из выражения (II.36), логарифм константы скорости линейно зависит от обратной температуры (рис.2.7); величину энергии активации E_A и логарифм предэкспоненциального множителя A можно определить графически (тангенс угла наклона прямой к оси абсцисс и отрезок, отсекаемый прямой на оси ординат).

(II.38)

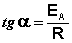
Зная энергию активации реакции и константу скорости при какой-либо температуре T₁, по уравнению Аррениуса можно рассчитать величину константы скорости при любой температуре T₂:

(II.39)

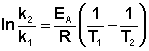
Copyright © С. И. Левченков, 1996 — 2005.

Видео:Использование уравнения Аррениуса для решения задач (1/2). Химия для поступающих.Скачать

График Аррениуса и определение энергии активации температурных реакций

Уравнение Аррениуса – это температурная зависимость константы скорости К элементарной химической реакции:

где A – предэкспоненциальный множитель (размерность совпадает с размерностью К), Еа-энергия активации, обычно принимающая положительные значения, Т – абсолютная температура, k-постоянная Больцмана. Принято приводить Еав расчете не на одну молекулу, а на число частиц NA= 6,02*1023(постоянная Авогадро) и выражать в кДж/моль; в этих случаях в уравнении Аррениуса величину k заменяют газовой постоянной R.

График зависимости 1nК от 1/kT (график Аррениуса) – прямая линия, отрицательный наклон которой определяется энергией активации Еа и характеризует положительную температурную зависимость К.

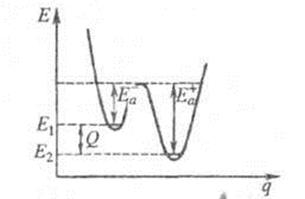
Энергия активации в элементарных реакциях, минимальная энергия реагентов (атомов, молекул и др. частиц), достаточная для того, чтобы они вступили в химическую реакцию, т. е. для преодоления барьера потенциальной энергии на поверхности, отделяющего реагенты от продуктов реакции. Потенциальный барьер — максимум потенциальной энергии, через который должна пройти система в ходе элементарного акта химического превращения. Высота потенциального барьера для любого пути, проходящего через переходное состояние, равна потенциальной энергии в переходном состоянии. Если в сложной реакции, состоящей из последовательных и параллельных элементарных реакций, имеется лимитирующая элементарная реакция (реакция с максимальным характерным временем), то ее энергия активации является и энергией активации сложной реакции. В макроскопической химической кинетике энергия активации – энергетический параметр Еа, входящий в уравнение Аррениуса К=Аexp(-Е_а / RТ). Наблюдаемая энергия активации вычисляется из тангенса угла наклона прямой графика Аррениуса. В общем случае сложных реакций параметр Еа в уравнении Аррениуса является функцией энергии активации отдельных стадий, и определяемая энергия активации называется эффективной (эмпирической, кажущейся). Любой процесс, сопровождающийся каким-либо изменением энергии, является экзотермическим в одном направлении и эндотермическим в другом. Энергии активации экзотермического и эндотермического направлений реакции, обозначаемые соответственно Е — _а и Е + _а , связаны соотношением: Е + _а=Е — _а+|Q|, где Q — .теплота реакции при Т=0. Качественная одномерная геометрическая иллюстрация связи энергии активации с высотой потенциального барьера и теплотой реакции представлена на рисунке, где q -координата реакции; Е₁ и Е₂ — уровни энергии соответственно основного состояния реагентов и продуктов реакции.

Энергетическая схема элементарной реакции.

Аналитическое применение методов ДТА и ДСК.

Позволяет проводить анализ изменения массы и тепловых потоков в одном эксперименте для одного и того же образца. Сочетая методы ТГА (термографический анализ) и ДСК, можно определить следующие характеристики материалов: с помощью ТГА фиксируется изменение массы образца при программируемом изменении температуры, при этом так же определяется массовый остаток вещества после термовоздействия.

С помощью ДСК определяются следующие характеристики: теплота плавления кристаллических веществ, удельная теплоемкость в широком диапазоне температур, температура стеклования полимерных материалов, степень кристалличности энтальпия реакции термостойкость и устойчивость к окислению старение материалов чистота веществ фазовые переходы, полиморфные превращения идентификация продукта по набору теплофизических характеристик.

Можно проводить анализ:

· температуры фазовых переходов

· поведения при кристаллизации

Лекция 6.

Термогравиметрия.

Наряду с методом дифференциально-термического анализа веществ активно развивалась и вторая ветвь термического анализа – метод термогравиметрии. С помощью последнего можно с высокой степенью точности проследить за изменением массы пробы при повышении температуры.

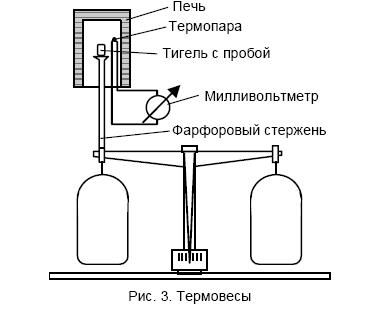
Термогравиметрия – это метод исследования, заключающийся в измерении изменения массы образцов при нагревании. Первоначальную схему метода можно представить следующим образом: пробу нагревали до определенной температуры, затем охлаждали и после охлаждения взвешивали с аналитической точностью. Процесс повторяли циклически, каждый раз увеличивая температуру. Если результаты взвешивания, относящиеся к отдельным температурным значениям, представить в координатах температура – масса образца и соединить полученные точки, то получится кривая, именуемая термогравиметрической (ТГ). Описанный метод является исключительно длительным и неточным, но применяется и сегодня, например, при аналитическом определении потери массы при прокаливании вещества. Значительно быстрее и точнее проводить измерения с помощью термовесов, непрерывно регистрирующих изменение массы пробы.

Принцип работы термовесов следующий. Пробу помещают в тигель (рис. 3), опирающийся на коромысло весов. Затем тигель нагревают в электрической печи так, чтобы его температура равномерно повышалась. Температура печи измеряется с помощью находящейся в ней термопары, к концам которой подключен милливольтметр, и время от времени (например, каждые 5. 10 К) масса образца фиксируется.

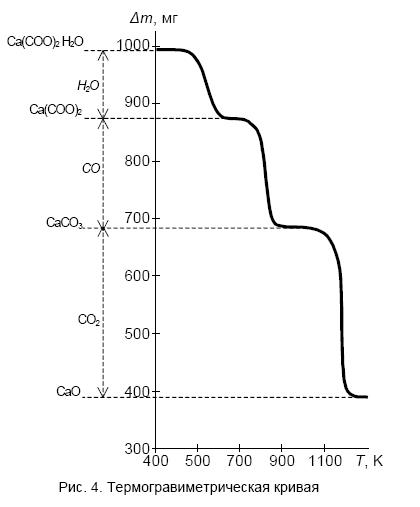
Графически изображенные результаты измерения дают термогравиметрическую кривую (рис. 4). Если изменение массы регистрируется автоматически, кривая ТГ строится в зависимости не от температуры, а от времени, однако такая замена оси абсцисс обратима, если одновременно фиксируется и зависимость температуры в печи от времени. Наиболее просто замена оси абсцисс осуществляется в том случае, когда повышение температуры в печи происходит равномерно во времени.

На основании кривой ТГ можно судить о том, каким образом изменялась при нагревании масса пробы, например, при каких температурах и на сколько миллиграммов менялась масса пробы осадка ацетата кальция, а следовательно, при каких температурах происходили химические превращения Ca(СОО)₂*H₂O → Ca(СОО)₂ → CaСО₃ → CaО.

Степень изменения массы определяется в зависимости от типа термовесов с точностью, примерно, от 0.1 до 0.5%, поэтому на основании результатов измерения можно производить довольно точные стехиометрические расчеты (стехиометрия – наука о соотношении массовых или объемных долей реагирующих веществ).

Конструкция термовесов постоянно модифицировалась. Первый экземпляр термовесов сконструировал японский исследователь Гонда в 1915 г. Впоследствии многие исследователи шли по пути совершенствования именно его конструкции. Среди используемых в настоящее время есть весы, качающиеся по призмам, весы с подвешенным коромыслом, весы с тормозящей нитью, весы пружинного типа, весы, снабженные жидкостным, воздушным или электромагнитным затуханием. Но, рассуждая объективно, ни одному из многочисленных типов нельзя отдать безусловное предпочтение.

Как изучение процессов, происходящих при нагревании глинистых минералов и пород, потребовало широкого распространения и развития метода ДТА, так и нерешенные вопросы определения постоянного состава аналитических осадков ускорили распространение метода термогравиметрии. Для исследования же иных вопросов последний метод долгое время применялся очень редко.

Недостатки термогравиметрии обнаруживаются только тогда, когда целью испытания является определение хода процесса разложения. Кроме того, в тех случаях, когда две реакции следуют плотно друг за другом либо перекрывают друг друга или же чередуются реакции с большими и небольшими изменениями массы, тогда метод термогравиметрии оказывается неопределенным и оценка кривой становится затруднительной и неточной.

Указанные трудности попытались устранить конструированием вакуумных термовесов. Сущность термогравиметрических испытаний в вакууме заключается в том, что выделившиеся газообразные побочные продукты немедленно удаляются из внутренней части материала, вследствие чего равновесие реакций разложения смещается в сторону разложения. Между твердой и газообразной фазами всегда устанавливается равновесие, изменяющееся в соответствии с парциальным давлением газовых продуктов. Термическое разложение в вакууме обычно происходит в узких температурных пределах и быстро, поэтому плотно следующие друг за другом реакции лучше отделяются друг от друга.

Эти же проблемы вынудили исследователей разработать новый статический метод термогравиметрии, который был назван ими методом ступенчатого изотермического нагревания. Такой метод испытания несмотря на применение в нем автоматически работающих современных термовесов в действительности означал возвращение к старому методу периодического нагревания и взвешивания. Температуру печи при испытании не увеличивали до тех пор, пока масса пробы не становилась постоянной. Затем, незначительно увеличив температуру, опять дожидались постоянства массы. Таким способом удалось достичь того, что даже в случае медленно происходящих процессов устанавливалось равновесие, соответствующее данной температуре, и реакции, происходящие при более низкой температуре, не смешивались с реакциями, протекающими при более высокой. Полученные кривые показывают резкие и определенные переломы, значительно облегчающие оценку. Однако применение этого метода целесообразно лишь в исключительных случаях, так как процесс измерения является весьма длительным.

Таким образом, несмотря на всевозможные ухищрения, предпринимаемые для устранения трудностей оценки кривой ТГ, исследователям стало ясно, что необходим качественно новый подход к измерению.

🎦 Видео

8 класс, 21 урок, Графическое решение уравненийСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

7 класс, 35 урок, Графическое решение уравненийСкачать

Влияние температуры на скорость химических реакций. 10 класс.Скачать

Порядок реакции и энергия активацииСкачать

ГРАФИК ЛИНЕЙНОГО УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСС видеоурокСкачать

ЛЕКЦИЯ №12 || Химическая кинетика || Автокатализ, уравнение Аррениуса, энергия активацииСкачать

Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать

Лекция 8: уравнение Аррениуса (30.10.2019)Скачать

Лекция 13 || 2021 || Температурная зависимость скорости, уравнение Аррениуса, энергия активацииСкачать

Теории кислот, оснований и растворов. Теория Аррениуса-Оствальда. 11 класс.Скачать

7 класс, 8 урок, Линейное уравнение с двумя переменными и его графикСкачать

Уравнение Аррениуса, часть 1Скачать

ДВИ по химии. Термохимия. Уравнение Аррениуса, закон Гесса, задачи на теплоемкостьСкачать

6 Уравнение Аррениуса, ч 2Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

С.Аррениус. Определение кислоты как вещества (видео 1) | Кислоты и Основания | ХимияСкачать

Химическая кинетика. Формальная кинетика простых гомогенных реакций в закрытых системахСкачать