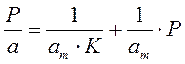Графически определите константы в уравнении лэнгмюра пользуясь которыми постройте изотерму ленгмюра

Конечно, предположение, что молекулы адсорбируются с одинаковой вероятностью на любых участках поверхности, в том числе и уже занятых ранее — слишком грубое допущение, пригодное лишь для очень малых степеней покрытия.

Теория Ленгмюра позволяет учесть наиболее сильные отклонения от закона Генри, что связано с ограничением адсорбционного объема или поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества. Это положение уточняется следующими утверждениями.

1) Адсорбция локализована на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбента — образуется мономолекулярный слой.

2) Адсорбционные центры энергетически эквивалентны — поверхность адсорбента эквипотенциальна.

3) Адсорбированные молекулы не взаимодействуют друг с другом.

Простейший вывод уравнения Ленгмюра, данный Кисилевым, основан на рассмотрении химического (в случае хемосорбции) или квазихимического (в случае физической адсорбиии) равновесия молекула газа + свободное место↔адсорбированная молекула.

Для обычного выражения константы равновесия через концентрации участников рассматриваемого процесса необходимо условиться о способах их выражения. Концентрация адсорбированных молекул может быть выражена не только числом адсорбированных молекул на 1 м 2 поверхности, но и в относительных единицах через долю занятой поверхности (степень заполнения поверхности) θ. Тогда, в тех же единицах, концентрация свободных мест 1-θ. Концентрация молекул газа (а молях на миллилитр) может быть заменена пропорциональной ей величиной давления Р (равновесное давление адсорбата в объеме фазы, граничащей с адсорбентом). Такая свобода в выборе единиц рассматриваемых концентраций обусловлена тем, что соответствующие константы пропорциональности могут быть объединены с константой равновесия. Итак, константа равновесия

. (2.6)

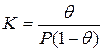
Решение этого уравнения относительно θ приводит к выражению

. (2.7)

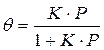
Если а, как и раньше, есть величина адсорбции (моль/см 2 или см 3 /г), а a_m — величина адсорбции, соответствующая полному заполнению поверхности (емкость монослоя, моль/см 2 ), то степень заполнения θ=a/a_m, (2.8)

т.е. 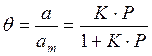, (2.9)

отсюда 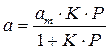(2.10)

В такой форме уравнение Ленгмюра широко известно. Оно содержит две константы: a_m, кратко называемая емкостью монослоя, и K — константа, зависящая от энергии адсорбции и температуры.

Итак, уравнение Ленгмюра – это уравнение монослойной адсорбции на однородной поверхности в отсутствие сил притяжения между молекулами адсорбата.

Посмотрим, какую форму примет уравнение при крайних значениях поверхностной концентрации адсорбированного вещества.

В области малых концентраций, т.е. при малых давлениях, КР >1, и единицей в знаменателе можно пренебречь:

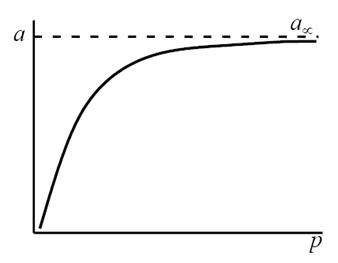
т.е. величина адсорбции стремится к пределу, при котором она уже практически не зависит от давления (участок 3 изотермы адсорбции). В промежуточной области (участок 2) зависимость адсорбции от давления описывается самим уравнением (2.10).

Рис. 2.5. Три участка изотермы адсорбции Ленгмюра

Таким образом, по модели Ленгмюра, вначале адсорбция растет пропорционально давлению газа, затем, по мере заполнения мест на поверхности, этот рост замедляется и, наконец, при достаточно высоких давлениях рост адсорбции практически прекращается, так как покрытие поверхности становится весьма близким к монослойному. Необходимо подчеркнуть, однако, что по этой модели завершение образования монослоя происходит лишь при бесконечно высоком давлении. Форма изотермы адсорбции, предсказываемая уравнением Ленгмюра, экспериментально наблюдается в случае химической адсорбции на однородных поверхностях. Для физической адсорбции такое соответствие наблюдается только в начальной области изотермы. При больших заполнениях не получается предсказываемого теорией приближения к насыщению и изотерма продолжает подъем с ростом давления, причем она становится даже более крутой.

Для удобной проверки приложимости уравнения Ленгмюра к экспериментальным данным преобразуем его в линейную форму. Разделим обе части уравнения (2.10) на Р:

. (2.13)

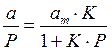
Перевернем дроби по обе части равенства:

. (2.14)

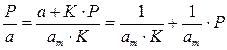
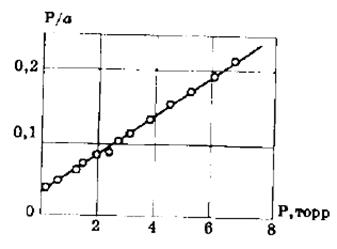
Если по оси абсцисс откладывать Р, а на оси ординат Р/а, то в случае выполнимости уравнения Ленгмюра экспериментальные точки должны укладываться на прямую. Начальной ординатой будет 1/(а_m∙К), тангенсом угла наклона прямой 1/а_m. Из того и другого выражения легко вычислить обе константы a_m и К. Пример такого построения показан на рис. 2.6, где экспериментальные точки для адсорбции бензола на графитированной саже, в соответствии с указанными ранее, легли па прямую только в области малых давлений (до Р/Р₀ =0.1).

Рис. 2.6. Изотерма адсорбции бензола при 20 о С на графитированной саже в координатах линейной формы уравнения Ленгмюра

Имеется немало примеров, когда уравнение Ленгмюра не выполняется. Объясняется это тем, что не оправдываются оба допущения теории об однородности поверхности и отсутствии взаимодействия молекул, особенно первое из них. Тот факт, что имеются случаи адсорбции на реальных неоднородных поверхностях, когда уравнение Ленгмюра все же удовлетворительно описывает экспериментальные данные, Брунауер объясняет тем, что в некотором интервале адсорбция происходит не на всей поверхности адсорбента, а только на части ее, именно на местах с примерно одинаковой теплотой адсорбции. Тогда в этом интервале уравнение Ленгмюра будет справедливо. После того, как эти места заполнены, начинает заполняться следующая серия мест с меньшей теплотой адсорбции. Поэтому для совокупности всех мест поверхности уравнение Ленгмюра может быть непригодно, а для части этих мест — справедливо. Отсюда, выполнимость его для разных адсорбентов зависит от соотношения участков с разной теплотой адсорбции.

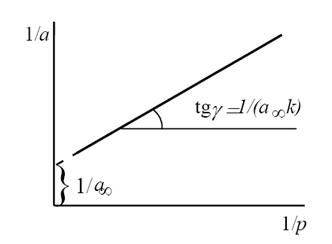
Константы уравнения (2.10) K и a_m могут быть определены графическим способом (рис. 2.7). Для этого уравнение Ленгмюра приводят к следующему линейному виду, разделив единицу на уравнение (2.10):

(2.15)

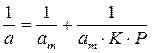
Рис. 2.7. Линейная форма уравнения изотермы Ленгмюра (a_∞=a_m)

Зная емкость монослоя, можно определить удельную поверхность адсорбента S_уд (м 2 /г или см 2 /г) если известна площадь ω, занимаемая частицей в плотном адсорбционном слое (площадь, занимаемая одной молекулой азота в адсорбционном слое ω = 0.162 нм 2 ):

, (16)

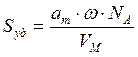
где а_m — емкость монослоя — это количество адсорбата, которое может разместиться в полностью заполненном адсорбционном слое толщиной в 1 молекулу — монослое – на поверхности единицы массы (1г) твердого тела; ω — средняя площадь, занимаемая молекулой адсорбата в заполненном монослое, N_A — число Авогадро (6,022·10 23 молекул/моль); V_M — молярный объем адсорбата (газа) (V_M = 22,41 л/моль=22,41∙10 -3 м 3 /моль).

Уравнение Ленгмюра можно использовать только при адсорбции в мономолекулярном слое. Это условие выполняется при хемосорбции, физической адсорбции газов при меньшем давлении и температуре выше критической.

Однако в большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поэтому остается возможность влияния поверхностных сил на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и пары адсорбируются при температуре ниже критической, т.е. образуются полимолекулярные слои на поверхности адсорбента, что можно представить как вынужденную конденсацию В этом случае используют уравнение БЭТ (Брунауер –Эммет — Теллер).

Пример 2.1. При адсорбции азота на активированном угле при 220К получены следующие данные:

Р, Па 5310 9800 18000 33000 70000

a, cм 3 /г 7 14 23 32 51

Плотность газообразного азота ρ=1,2506 кг/м 3 . Площадь, занимаемая одной молекулой азота в насыщенном монослое, составляет ω = 0.162 нм 2 . V_M — молярный объем адсорбата (газа) (V_M = 22,41 л/моль=22,41∙10 -3 м 3 /моль).

Постройте изотерму адсорбции в линейных координатах. Графически определите константы а_m и К уравнения Ленгмюра, пользуясь которыми, постройте изотерму Ленгмюра. Определите удельную поверхность активированного угля S_уд.

Решение. Линейная форма уравнения Ленгмюра выражается (2.15):

.

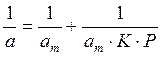
Определим 1/а_m и 1/ р:

(1/р)·10 -3 , Па 0,1883 0,1020 0,0556 0,0303 0,0143

1/а·, см 3 /г 0,143 0,071 0,043 0,031 0,020

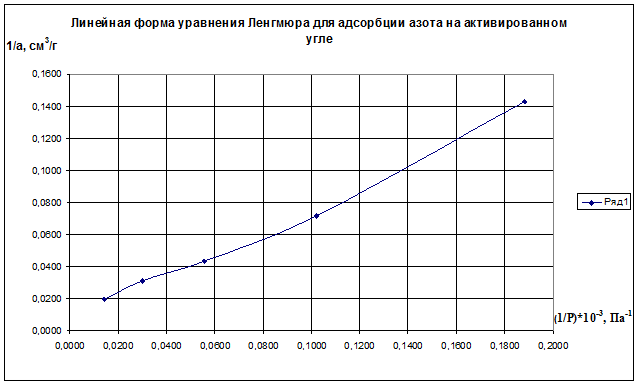
Строим график зависимости 1/а=f(1/р)∙10 -3 (рис.2.8). По графику находим 1/а_m как отрезок, отсекаемый прямой на оси ординат, для чего необходимо продлить полученную прямую до пересечения с осью ординат.

Рис.2.8. Линейная форма уравнения Ленгмюра для адсорбции азота на активированном угле

Уравнение прямой y=a+bx, имеет следующее формульное выражение:

Это выражение может быть определено с помощью регрессионного анализа в Microsoft Excel (встроенного пакета Анализ данных — Регрессия по значениям 1/а_m и 1/ р).

Из уравнения получим 1/a_m=0,00698 г/см 3 .

Откуда получим: a_m=143,35 см 3 /г.

Далее находят тангенс угла наклона прямой к оси абсцисс tgα=1/(a_m∙K) по графику (или по уравнению регрессии). tgα=0,70099. Тогда, зная значения a_m и tgα, можно определить K=9,95 кг/м 3 .

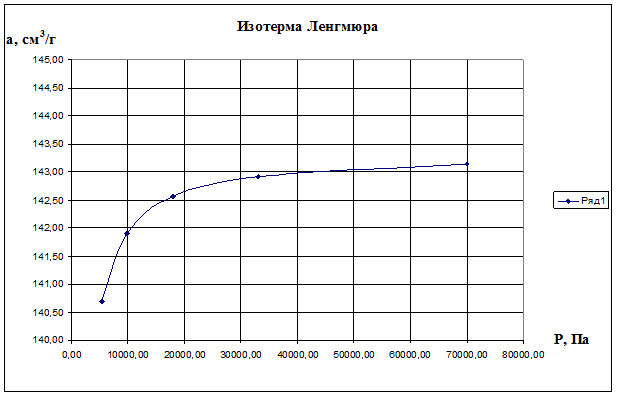
Теперь, зная константы а_m и К уравнения Ленгмюра, построим изотерму Ленгмюра, для чего рассчитаем по формуле (2.10) значения а для различных значений Р и получим:

Р, Па 5310 9800 18000 33000 70000

a, cм 3 /г 140,69 141,90 142,56 142,92 143,15

По данным значениям построим изотерму Ленгмюра а=f(P), представлена на рис.2.9.

Рис. 2.9. Изотерма Ленгмюра а=f(P)

По формуле (2.16) рассчитаем удельную поверхность активированного угля: 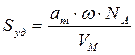и получим S_уд=624,05 м 2 /г.

В случае, когда известна плотность вещества (адсорбента) ρ и молярная масса M, а не известен V_M — молярный объем адсорбата удельную поверхность вещества (активированного угля) находят по формуле:

где a_m выражают в моль/кг.

Для азота М= 0,0280 кг/моль, ρ=1,2506 кг/м 3 .

Из расчетов видно, что два способа расчета S_уд дают почти одинаковые результаты.

Пример 2.2. Удельная поверхность непористой сажи равна 73,7м 2 /кг. Рассчитайте площадь, занимаемую молекулой бензола в плотном монослое, исходя из данных об адсорбции бензола на этом адсорбенте при 293 К.

Р, Па 1,03 1,29 1,74 2,50 6,67

а∙10 2 , моль/кг 1,57 1,94 2,55 3,51 7,58

Предполагается, что изотерма адсорбции описывается уравнением Ленгмюра.

Решение. Используем линейную форму записи уравнения Ленгмюра, заданную формулой (2.14):

Рассчитываем значения Р/а:

(Р/а)∙10 -2 , Па∙кг/моль 0,656 0,668 0,68 0,712 0,879

Р, Па 1,03 1,29 1,74 2,50 6,67

По этим данным строим график в координатах уравнения Ленгмюра в линейной форме P/a=f(P).

Из графика находим а_m= Р/(Р/а) = 25,2∙10 -2 моль/кг.

Удельная поверхность адсорбента связана с емкостью слоя а_m, выраженного в моль/кг, соотношением: S_уд=a_m∙ω∙N_A (2.18)

Площадь, занимаемая молекулой бензола в плотном монослое, равна

ω = S_уд/(a_m N_A) ==73,7 10 3 /(6,02 10 23 ∙25,210 -2 )=0,49∙10 -18 м 2 =0,49 нм 2 .

Видео:Решение задач на тему: "Нахождение константы равновесия и равновесных концентраций". 3ч. 10 классСкачать

По экспериментальным данным адсорбции фенола на ионите при 473 К графически определите

• Реферат.Справочник
• Решенные задачи по химии
• По экспериментальным данным адсорбции фенола на ионите при 473 К графически определите

Условие

По экспериментальным данным адсорбции фенола на ионите при 473 К графически определите: а) константы уравнения Фрейндлиха и Ленгмюра; б) запишите уравнения Фрейндлиха и Ленгмюра с учётом полученных констант; в) пользуясь константами уравнения Ленгмюра, постройте изотерму адсорбции Ленгмюра. С∙102, моль/л 1,5 4,5 7,5 9,0 А∙103, кг/кг 0,52 1,13 1,35 1,40

Видео:ВАЛЕНТНОСТЬ. Графические формулы веществ | Химия | TutorOnlineСкачать

Нужно полное решение этой работы?

Решение

Чтобы найти константы уравнения Фрейндлиха, необходимо по экспериментальным данным построить изотерму Фрейнлиха в линейных координатах lgА = f(lgС). Вычислим lgА и lgС и запишем в таблицу.
С∙102, моль/л 1,5 4,5 7,5 9,0
А∙103, кг/кг 0,52 1,13 1,35 1,40
lgС -1,823 -1,347 -1,125 -1,046
lgА -3,284 -2,947 -2,870 -2,854
Строим график (рис. 3).
Рисунок 3. Изотерма адсорбции в логарифмических координатах
Для определения уравнения прямой используем метод наименьших квадратов. Примем, что lgС = х и lgА = у, п = 4.
∑
х -1,823 -1,347 -1,125 -1,046 -5,341
у -3,284 -2,947 -2,87 -2,854 -11,955
х∙у 5,986732 3,969609 3,22875 2,985284 16,170375
х2 3,323329 1,814409 1,265625 1,094116 7,497479
a=n∙xi∙yi-xi∙yin∙xi2-xi2; b=yi-a∙xin;
a=4∙(16,17)—5,341∙(-11,955)4∙7,50—5,3412=0,567;
b=-11,955+0,567∙5,3414=-2,23.
Уравнение прямой имеет вид
lgА = — 2,23 + 0,567∙lgС.
Сравним полученное уравнение с линейной формой уравнения Фрейндиха: lgА = lgK + 1n∙lgС

Зарегистрируйся, чтобы продолжить изучение работы

. Очевидно, что lgK = — 2,23, откуда К = 10-2,23 = 5,9∙10-3 и 1n = 0,567.
С учётом найденных констант уравнение Фрейндлиха имеет вид
А = 5,9∙10-3∙С0,567.
Чтобы найти константы уравнения Ленгмюра, построим график в координатах С/А = f(С). Вычислим значения р/А и запишем их в таблицу.
С∙102, моль/л 1,5 4,5 7,5 9,0
А∙103, кг/кг 0,52 1,13 1,35 1,40
С/А, моль кг/л кг 28,85 39,82 55,55 64,28
График С/А = f(С) изображён на рис. 4.
Для определения уравнения прямой используем метод наименьших квадратов

Оплатите решение задач или закажите уникальную работу на похожую тему

Видео:Решение задач на тему: "Нахождение константы равновесия и равновесных концентраций". 4ч. 10 класс.Скачать

По экспериментальным данным адсорбции фенола на ионите при 423 К графически определите константы в уравнении Лэнгмюра, пользуясь которыми

Готовое решение: Заказ №8423

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Химия

Дата выполнения: 05.09.2020

Цена: 228 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

По экспериментальным данным адсорбции фенола на ионите при 423 К графически определите константы в уравнении Лэнгмюра, пользуясь которыми, постройте изотерму адсорбции Лэнгмюра

Решение:

В линейной форме уравнение Ленгмюра имеет вид

Вначале рассчитаем значения с/А

с/А·10 -4 ,

Для переводя адсорбции в моль/кг воспользовались формулой:

A=A*ρ/M, где ρ – плотность газа, а М = молярная масса.

• По изотерме адсорбции бензола при 293 К рассчитайте удельную поверхность адсорбента, если площадь, занимаемая одной молекулой бензола S0 = 0,49 нм2
• С помощью метода поточной ультрамикроскопии в объеме равном 2,2·10-11 м 3 подсчитано 80 частиц дыма мартеновских печей
• Золь ртути состоит из шариков диаметром 6.10-6 см. Чему равна: а) суммарная площадь поверхности частиц; б) общее число частиц в растворе
• Свежеосажденный осадок гидроксида алюминия обработали небольшим количеством соляной кислоты, недостаточным для полного растворения осадка

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

📹 Видео

Решение задач на тему: "Нахождение константы равновесия и равновесных концентраций". 2ч. 10 класс.Скачать

Поверхностные явления. Адсорбция на подвижных границах раздела фаз.Скачать

Поверхностные явления: адгезия, смачивание, адсорбция | Коллоидная химияСкачать

Метод молекулярных орбиталей. Часть 1. Основные понятия.Скачать

АдсорбцияСкачать

Решение задач на термохимические уравнения. 8 класс.Скачать

Урок 16. Определение валентности элементов по формулам их соединений (8 класс)Скачать

11 класс.Элементы 4 периода.Электронные формулы.Скачать

Теории кислот, оснований и растворов. Теория Аррениуса-Оствальда. 11 класс.Скачать

Экзо- и эндотермические реакции. Тепловой эффект химических реакций. 8 класс.Скачать

Расчеты по уравнениям химических реакций. 1 часть. 8 класс.Скачать

Гибридизация и геометрические формы молекул доступным языком. (Общая химия)Скачать

Изопроцессы. Графики изопроцессов. Закон Дальтона. 1 часть. 10 класс.Скачать

Обратная функция, свойства, график. Как найти функции обратные данным и построить график. 8-11 классСкачать

Буферные системы, ацидоз и алкалоз, ур-ие Гендерсона-Гассельбаха (Атриум и Учим химию)Скачать

Построение изотермы адсорбцииСкачать

Как ЛЕГКО понять Химию с нуля — Массовая доля вещества // ХимияСкачать