Горизонтальной асимптотой функции f ( x ) называется прямая параллельная оси x к которой неограниченно приближается функция f ( x ) при стремлении к бесконечности. Уравнение горизонтальной асимптоты записывается в виде
y = y 0 , где y 0 — некоторая константа (конечное число)
Для того, чтобы найти горизонтальную асимптоту функции f ( x ) , очевидно, необходимо найти y 0 . Получить значение y 0 можно вычислив пределы
Если значение хотя бы одного предела равно конечному числу y 0 , тогда
y = y 0 — горизонтальная асимптота функции f ( x ) .
Для вычисления горизонтальных асимптот своей функции Вы можете воспользоваться нашим бесплатным онлайн калькулятором, построенным на основе системы Wolfram Alpha.
Асимптоты
п.1. Понятие асимптоты
Различают вертикальные, горизонтальные и наклонные асимптоты.
Например:
 Вертикальная асимптота x=3 |  Горизонтальная асимптота y=1 |
 Наклонная асимптота y=x | |
п.2. Вертикальная асимптота
Таким образом, практически каждой точке разрыва 2-го рода (см. §40 данного справочника) соответствует вертикальная асимптота.
Вертикальных асимптот может быть сколько угодно, в том числе, бесконечное множество (например, как у тангенса – см. §6 данного справочника).
Например:
Исследуем непрерывность функции (y=frac)
ОДЗ: (xne left)
(leftnotin D) — точки не входят в ОДЗ, подозрительные на разрыв.
Исследуем (x_0=-3). Найдем односторонние пределы: begin lim_frac=frac=frac=+infty\ lim_frac=frac=frac=-infty end Односторонние пределы не равны и бесконечны.
Точка (x_0=-3) — точка разрыва 2-го рода.
Исследуем (x_1=1). Найдем односторонние пределы: begin lim_frac=frac=frac=-infty\ lim_frac=frac=frac=+infty end Односторонние пределы не равны и бесконечны.
Точка (x_1=1) — точка разрыва 2-го рода.
Вывод: у функции (y=frac) две точки разрыва 2-го рода (left), соответственно – две вертикальные асимптоты с уравнениями (x=-3) и (x=1).
п.3. Горизонтальная асимптота
Число горизонтальных асимптот не может быть больше двух.
Например:
Исследуем наличие горизонтальных асимптот у функции (y=frac)
Ищем предел функции на минус бесконечности: begin lim_frac=frac=+0 end На минус бесконечности функция имеет конечный предел (b=0) и стремится к нему сверху (о чем свидетельствует символическая запись +0).
Ищем предел функции на плюс бесконечности: begin lim_frac=frac=+0 end На плюс бесконечности функция имеет тот же конечный предел (b=0) и также стремится к нему сверху.
Вывод: у функции (y=frac) одна горизонтальная асимптота (y=0). На плюс и минус бесконечности функция стремится к асимптоте сверху.
Итоговый график асимптотического поведения функции (y=frac): 
п.4. Наклонная асимптота
Число наклонных асимптот не может быть больше двух.
Чтобы построить график асимптотического поведения, заметим, что у функции (y=frac), очевидно, есть вертикальная асимптота x=1. При этом: begin lim_frac=-infty, lim_frac=+infty end
График асимптотического поведения функции (y=frac): 
п.5. Алгоритм исследования асимптотического поведения функции
На входе: функция (y=f(x))
Шаг 1. Поиск вертикальных асимптот
Исследовать функцию на непрерывность. Если обнаружены точки разрыва 2-го рода, у которых хотя бы один односторонний предел существует и бесконечен, сопоставить каждой такой точке вертикальную асимптоту. Если таких точек не обнаружено, вертикальных асимптот нет.
Шаг 2. Поиск горизонтальных асимптот
Найти пределы функции на плюс и минус бесконечности. Каждому конечному пределу сопоставить горизонтальную асимптоту. Если оба предела конечны и равны, у функции одна горизонтальная асимптота. Если оба предела бесконечны, горизонтальных асимптот нет.
Шаг 3. Поиск наклонных асимптот
Найти пределы отношения функции к аргументу на плюс и минус бесконечности.
Каждому конечному пределу k сопоставить наклонную асимптоту, найти b. Если только один предел конечен, у функции одна наклонная асимптота. Если оба значения k конечны и равны, и оба значения b равны, у функции одна наклонная асимптота. Если оба предела для k бесконечны, наклонных асимптот нет .
На выходе: множество всех асимптот данной функции.
п.6. Примеры
Пример 1. Исследовать асимптотическое поведение функции и построить схематический график:
a) ( y=frac )
1) Вертикальные асимптоты
Точки, подозрительные на разрыв: (x=pm 1)
Односторонние пределы в точке (x=-1) begin lim_frac=frac=frac=-infty\ lim_frac=frac=frac=+infty end Точка (x=-1) — точка разрыва 2-го рода
Односторонние пределы в точке (x=1) begin lim_frac=frac=frac=-infty\ lim_frac=frac=frac=+infty end Точка (x=1) — точка разрыва 2-го рода
Функция имеет две вертикальные асимптоты (x=pm 1)
График асимптотического поведения функции (y=frac)
2) Горизонтальные асимптоты
Пределы функции на бесконечности: begin b_1=lim_e^<frac>=e^0=1\ b_2=lim_e^<frac>=e^0=1\ b=b_1=b_2=1 end Функция имеет одну горизонтальную асимптоту (y=1). Функция стремится к этой асимптоте на минус и плюс бесконечности.
График асимптотического поведения функции (y=e^<frac>)
в) ( y=frac )
Заметим, что ( frac=frac=frac=frac ) $$ y=fracLeftrightarrow begin y=frac\ xne -1 end $$ График исходной функции совпадает с графиком функции (y=frac), из которого необходимо выколоть точку c абсциссой (x=-1).
3) Наклонные асимптоты
Ищем угловые коэффициенты: begin k_1=lim_frac=left[fracright]=lim_frac<x^2left(1+fracright)>=frac=1\ k_2=lim_frac=left[fracright]=lim_frac<x^2left(1+fracright)>=frac=1\ k=k_1=k_2=1 end У функции есть одна наклонная асимптота с (k=1).
Ищем свободный член: begin b=lim_(y-kx)= lim_left(frac-2right)= lim_frac= lim_frac=left[fracright]=\ =lim_frac=frac=1 end Функция имеет одну наклонную асимптоту (y=x+1).
График асимптотического поведения функции (y=frac)
2) Горизонтальные асимптоты
Пределы функции на бесконечности: begin b_1=lim_xe^<frac>=-inftycdot e^0=-infty\ b_2=lim_xe^<frac>=+inftycdot e^0=+infty end Оба предела бесконечны.
Функция не имеет горизонтальных асимптот.
График асимптотического поведения функции (y=xe^<frac>)
Асимптоты графика функции
Вы будете перенаправлены на Автор24
Достаточно часто на практике приходится иметь дело с функциями, которые определены не на всей числовой прямой, либо принимают не любые значения из множества действительных чисел.
В таких случаях при построении графиков функций получаем, что график функции не является непрерывной линией, а имеет некоторые разрывы. В результате чего становится целесообразным ввести понятие «асимптота».
Асимптота — это такая прямая, к которой график заданной функции приближается сколько угодно близко, но не пересекает ее.
Среди асимптот выделяют следующие виды:
- вертикальная асимптота (параллельна оси ОY);
- горизонтальная асимптота (параллельна оси ОХ);
- наклонная асимптота (расположена под углом к осям координат).
Отметим, что асимптоты на графике функции изображаются пунктирной линией.
Вертикальная асимптота — это прямая, определяемая уравнением $x=a$, для которой выполняются условия $mathoplimits_ f(x)=infty $ или $mathoplimits_ f(x)=infty $.
Вертикальная асимптота может быть только в точках разрыва функции $y=f(x)$, т.е. в тех точках, где данная функция неопределенна.
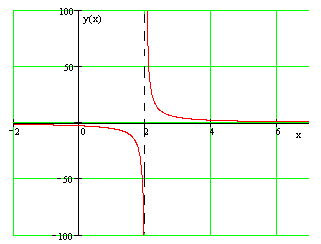
Найти вертикальную асимптоту графика данной функции: $y=frac $.
Следовательно, прямая $x=2$ является вертикальной асимптотой (см. рис.).
Горизонтальная асимптота — это прямая, определяемая уравнением $y=b$, для которой выполняются условия $mathoplimits_ f(x)=b$.
Готовые работы на аналогичную тему
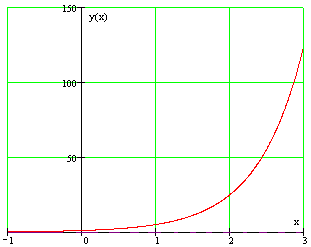
Найти горизонтальную асимптоту графика данной функции: $y=5^ $.
Следовательно, прямая $y=0$ является горизонтальной асимптотой (см. рис.).
График функции может иметь только правую либо только левую горизонтальную асимптоту.
Наклонная асимптота — это прямая, определяемая уравнением $y=kx+b$, для которой выполняется условие $mathoplimits_ [f(x)-kx+b]=0$.
Условия существования наклонной асимптоты определяются следующей теоремой.
Если функция $y=f(x)$ имеет конечные пределы $mathoplimits_ frac =k;mathoplimits_ [f(x)-kx]=b$, то данная функция имеет наклонную асимптоту, заданную уравнением $y=kx+b$ при $xto infty $.
Частным случаем наклонной асимптоты при $k=0$ является горизонтальная асимптота.
Наклонная асимптота может быть левой (график приближается справа), правой (график приближается слева) или двусторонней (график приближается с обоих сторон).
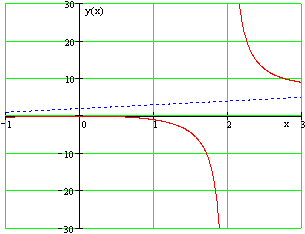
Найти наклонную асимптоту графика данной функции: $y=frac <x^> $.
Следовательно, прямая $y=x+2$ является наклонной асимптотой (см. рис.). В данном случае имеем двустороннюю наклонную асимптоту.
Найти наклонную асимптоту графика данной функции: $y=frac <x^> $.
Следовательно, график данной функции не имеет наклонной асимптоты.
График функции может иметь одновременно несколько асимптот, например, вертикальную и наклонную.
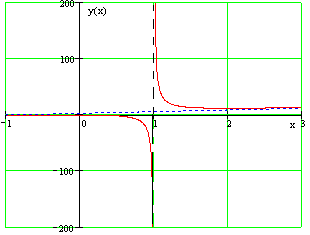
Найти асимптоты графика данной функции: $y=frac <3x^> $.
Область определения функции: $D_ = $.
Следовательно, прямая $x=1$ является вертикальной асимптотой (см. рис.).
Следовательно, прямая $y=3x+3$ является наклонной асимптотой (см. рис.). В данном случае имеем двустороннюю наклонную асимптоту.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 17.02.2022