Годограф скорости точки и его уравнения (5 видео)

Уравнение годографа вектора скорости

Содержание

Уравнение годографа вектора скорости
Годограф скорости
Построение годографа скоростей заданной точки
💥 Видео

Видео:Метод годографа и центростремительное ускорениеСкачать

Уравнение годографа вектора скорости

Уравнение движения декартовой точки известно. Получить уравнение годографа вектора скорости. На фиг. 9а показана траектория в момент времени и несколько векторов скорости в различные моменты времени в выбранном масштабе.

Регулярная прецессия гироскопа характеризуется собственным вращением и постоянной угловой скоростью прецессии, причем прецессия образуется вокруг оси в определенном направлении и под определенным углом. Людмила Фирмаль

На рисунке 9б показан годограф этого вектора скорости движения. Точка M (x, y, z) на траектории соответствует точке M (…, zj) на годографе вектора скорости. Согласно определению годографа, координаты точки Л / представляются проекцией вектора скорости на координатную ось OjXjjjjZi по формуле.

Если ось координат годографа вектора скорости параллельна оси относительных координат с учетом точечного уравнения движения, Z T М / х, у, зл Рисунок 9 rX) = vx = x; v „t = vy = y; vZt = vz = z. Параметрическое уравнение годографа вектора скорости имеет вид: Xj = x; yt = y; zr = z. Удаление параметра t из этих уравнений дает уравнение годографа для вектора скорости в координатной форме.

При получении постоянной вращающейся траектории вместо вертикального приближения Asym, как описано выше, получается наклонная асимптота в том или ином направлении в зависимости от направления вращения. Людмила Фирмаль

Годограф вектора скорости обеспечивает визуальное представление скорости движущейся точки в различные моменты времени. Кроме того, ускорение параллельно касательной к годографу вектора скорости, поэтому можно определить направление вектора ускорения.

Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать

Годограф скорости

ГОДОГРАФ СКОРОСТИ. Пусть точка перемещается по некоторой траектории АВ. В каждый момент времени вектор скорости (v) направлен по касательной к траектории в соответствующем положении точки, причем v = dr/dt, где r — радиус-вектор, определяющий положение точки на кривой по отношению к некоторой системе отсчета с произвольным началом О (фиг. 1). Вектор ускорения (а) равен производной вектора (v) по времени (t) а = dv/dt. Если от некоторой произвольной точки О₁ откладывать векторы h = v, то, при перемещении точки по своей траектории, вектор (h) будет менять в общем как свою абсолютную величину, так и направление, имея одно и то же начало О₁. Конец вектора (h) будет описывать кривую, называемую годографом скорости. Так как вектор (h) для кривой А₁В₁ играет ту же роль, что вектор (r) для кривой АВ, то скорость конечной точки вектора (h), при ее перемещении по А₁В₁, равна

Таким образом, видно, что вектор ускорения точки, движущейся по некоторой траектории, равняется в каждый момент соответствующему вектору скорости конца вектора, описывающего годограф скорости. Плоскость, касательная к годографу скорости и проходящая через (h), будет, очевидно, параллельна плоскости, проходящей через (а) и (v), т. е. она будет параллельна соприкасающейся плоскости кривой АВ.

При прямолинейном равномерном движении (v = Const) годограф скорости стягивается в одну точку. Если точка перемещается по кривой, имея одну и туже линейную скорость (v = Const), то годограф скорости представляет собой кривую, описанную на шаровой поверхности радиуса (v).

При плоском движении, годограф скорости — плоская кривая. Для свободной материальной точки, брошенной под углом к горизонту с некоторой начальной скоростью v₀, имеем: v = v₀ + gt, где v — вектор скорости точки по истечении времени (t), а g = Const — вектор ускорения силы тяжести. Так как h₀ = v₀ = Const, а вектор (gt) сохраняет постоянно вертикальное направление, то конец вектора (h = v) постоянно лежит на вертикали, т. е. годограф скорости для рассматриваемого случая представляет собой вертикальную прямую (фиг. 2).

Если точка описывает конического сечение с постоянной секториальной скоростью относительно фокуса конического сечения, то годограф скорости представляет собой окружность. Годограф скорости впервые был рассмотрен Гамильтоном, а затем Мёбиусом.

Источник: Мартенс. Техническая энциклопедия. Том 5 — 1929 г.

Видео:К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

Построение годографа скоростей заданной точки

Годографом скоростей называется кривая, которая является геометрическим местом точек конца вектора скорости. Годограф позволяет определить скорость точки в любой момент времени по модулю и линии действия.

Годограф выгодно строить для точек, совершающих криволинейное движение. Для этого откладываем векторы скоростей соответствующей точки, полученные на планах скоростей, из общего полюса р в их истинном направлении и в одном масштабе. Соединяем концы всех векторов плавной кривой.

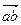
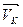
Для примера построим годограф скоростей точки К (точку К в механизме задаёт преподаватель). Пусть точка К делит звено АВ пополам. На всех двенадцати планах скоростей поделим векторы пополам. Ставим точку k. Соединяем её с полюсом плана скоростей. Полученные векторы (скорость точки К в масштабе – ) переносим в общий полюс р. Рядом с концом каждого вектора необходимо указать номер соответствующего положения кривошипа механизма.

Соединяем концы векторов плавной кривой (рис. 15).

Рис. 15. Годограф скоростей точки К.

Определение угловых скоростей звеньев механизма

Угловые скорости звеньев можно определить, используя относительные скорости построенного плана скоростей.

Угловая скорость первого звена была определена выше и равна ω₁=3,14 рад/с.

Модуль угловой скорости звена 2 найдём по формуле:

(8)

Для определения направления ω₂ необходимо мысленно перенести вектор относительной скорости из плана скоростей в точку В плана механизма (рис. 16), при этом видим, что вектор скорости стремится вращать точку В звена АВ относительно точки А против часовой стрелки, следовательно, и угловая скорость второго звена ω₂ будет направлена против часовой стрелки (т.е. положительно).

Аналогично определяем модули и направления угловых скоростей остальных звеньев.

Угловая скорость звена 3 по модулю равна:

и направлена против часовой стрелки.

Угловая скорость звена 4 по модулю равна:

и направлена против часовой стрелки.

Результаты расчета запишем в таблицу 5.

Таблица 5. Относительные скорости точек и угловые скорости

звеньев для двенадцати положений механизма.

скорости № положения	относительные скорости точек, м/с	угловые скорости звеньев, рад/с
V_B_А		V_D_С	w₂	w₃	w₄
0, 12
0,390	0,410	0,220	0,700	0,976	0,314

Направление угловых скоростей звеньев указано на схеме механизма (рис 16).

Рис. 16. Схема механизма с указанием направлений относительных линейных скоростей точек и угловых скоростей звеньев.

Определение линейных ускорений точек

Звеньев механизма

Определение линейных ускорений точек звеньев механизма происходит в той же последовательности, что и определение линейных скоростей. Пример построения плана ускорений выполнен для положения 5 механизма (рис. 17).

Первой точкой, ускорение которой надо определить, является точка А ведущего звена. Так как кривошип 1 вращается с постоянной угловой скоростью, то абсолютное ускорение точки А определяется только величиной нормального ускорения, которое по модулю равно:

. (9)

Вектор направлен вдоль кривошипа O₁A от точки А к оси вращения О₁.

На плоскости выбираем произвольную точку q (полюс плана ускорений), которая является началом отсчета и ускорение которой равно нулю. Откладываем от неё вектор (параллельно звену O₁A в направлении от точки А к точке О₁).

Длина этого вектора изображает на плане ускорений вектор ускорения точки А и выбирается так, чтобы площадь плана ускорений была равна примерно 150 см 2 . Примем длину вектора равным 98 мм, тогда масштабный коэффициент плана ускорений будет:

(10)

Рассмотрим первую группу Ассура, образованную звеньями 2 и 3. Ускорения точек А и О₂ известны. Определим ускорение точки В.

Оно складывается из абсолютного ускорения точки А и относительного ускорения точки В при вращении звена 2 вокруг точки А.

С другой стороны точка В принадлежит звену 3, и ее ускорение складывается из ускорения точки O₂ и относительного ускорения точки В при вращении звена 3 вокруг точки O₂.

Составим систему двух векторных уравнений:

. (11)

Так как точка В движется криволинейно, то относительные ускорения представим в виде суммы двух ускорений: нормального и тангенциального.

. (12)

Абсолютные величины нормальных ускорений определяются по формуле:

, (13)

Вектор нормального ускорения направлен вдоль звена АВ от точки В к точке А (к оси вращения), а нормального ускорения — вдоль звена BO₂ от точки В к точке O₂ (к оси вращения). Тангенциальные составляющие ускорений и по абсолютной величине неизвестны, но известны их линии действия. Они направлены перпендикулярно к нормальным составляющим (или перпендикулярно к соответствующим звеньям).

В системе уравнений (12) нам известны: ускорение точки А, ускорение точки O₂ ( =0), , и линии действия и . Эта система уравнений может быть решена графическим методом.

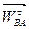
Рис. 17. Пример построения плана ускорений.

Через точку а плана ускорений проводим прямую, направленную вдоль звена АВ, и на ней откладываем вектор в направлении от точки В к точке А:

величина которого в масштабе соответствует величине вектора нормальной составляющей ускорения .

Через точку n₁, перпендикулярно к звену АВ (или то же самое, что перпендикулярно ) проводим линию действия вектора тангенциального ускорения .

Рассмотрим второе уравнение системы (12). Из полюса q (точка O₂ совпадает с полюсом q, т.к. её ускорение равно нулю) проводим прямую, параллельную звену O₂B. В направлении от точки В к точке O₂ (на плане механизма) откладываем на этой прямой отрезок qn₂, который в масштабе равен модулю вектора нормального ускорения :

Через точку n₂ перпендикулярно к звену O₂B проводим линию действия вектора тангенциального ускорения . Пересечение двух прямых на плане ускорений, изображающих линии действия тангенциальных ускорений, дает точку b.

Соединяя точку b с полюсом плана ускорений q, получим вектор , соответствующий на плане вектору абсолютного ускорения точки В механизма, величина которого равна:

Из плана ускорений можно определить абсолютную величину тангенциальных составляющих относительных ускорений:

Вектор относительного ускорения на плане ускорений показан штриховой линией и равен:

а вектор совпадает по величине и линии действия с вектором абсолютного ускорения .

Для определения ускорения точки C воспользуемся свойством подобия. Величина отрезка qc может быть найдена из соотношения:

; отсюда: .

Величина абсолютного ускорения точки C механизма равна:

Рассмотрим вторую группу Ассура, образованную звеньями 4 и 5. Определим ускорение точки D. Шатун 4 совершает плоско – параллельное движение, ползун 5 – прямолинейное поступательное движение (частный случай плоскопараллельного движения). Таким образом, точка D одновременно совершает два движения: вращательное относительно точки C и поступательное относительно неподвижной стойки. Ускорение точки D΄, связанной с неподвижной направляющей ползуна равно нулю.

Система уравнений для ускорения точки D будет имеет вид:

. (14)

Относительное ускорение 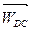представим в виде суммы двух составляющих — нормальной и тангенциальной.

. (15)

Величина нормального ускорения определяется по формуле:

Вектор нормального ускорения направлен вдоль звена CD от точки D к точке C (оси вращения). Тангенциальная составляющая по абсолютной величине неизвестна, но известна её линия действия. Она направлена перпендикулярно к нормальной составляющей. Вектор направлен вдоль направляющей.

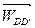
Система уравнений (12) имеет две неизвестные величины и решается графическим методом.

Через точку c плана ускорений проводим прямую, направленную вдоль звена CD в направлении от точки D к точке C, и на ней откладываем отрезок:

величина, которого в масштабе соответствует величине вектора нормальной составляющей ускорения .

Через точку n₃, перпендикулярно к звену CD (или то же самое, что перпендикулярно ) проводим линию действия вектора тангенциального ускорения . Рассмотрим второе уравнение системы (15). Из полюса q (т.к. ускорение D´=0 и совпадает с полюсом q) проводим прямую, параллельную направляющей ползуна х-х. Пересечение двух прямых на плане ускорений дает точку d. Полученный отрезок qd, соответствует на плане ускорений вектору абсолютного ускорения точки D механизма, величина которого равна:

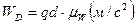
Из плана ускорений можно определить действительную величину тангенциальной составляющей относительного ускорения:

Вектор относительного ускорения шарниров звена на плане ускорений показан штриховой линией и равен:

Заполним таблицу 6.

Таблица 6. Относительные ускорения шарниров звеньев для

двух положений механизма, м/с 2 .

№ положе- ния ускорение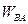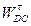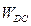
0,272	0,860	0,900	0,402	1,06	1,13	0,069	0,260	0,270

Определим ускорения центров тяжести звеньев S₂, S₃ и S₄ при помощи свойства подобия. Найдем положения точек центров тяжести на плане ускорения. Предположим, что центры тяжести s₂, s₃ и s₄ находятся посередине звеньев и делят векторы , , и пополам (рис.18). Центр тяжести ползуна 5 совпадает с точкой D, поэтому точка s₅ на плане скоростей совпадает с точкой d.

Рис. 18. Определение ускорений центров тяжести звеньев механизма

Соединим полученные точки s₂, s₃, s₄ и s₅ с полюсом q плана ускорений, тогда векторы , , и будут в масштабе изображать ускорение центра тяжести соответствующего звена.