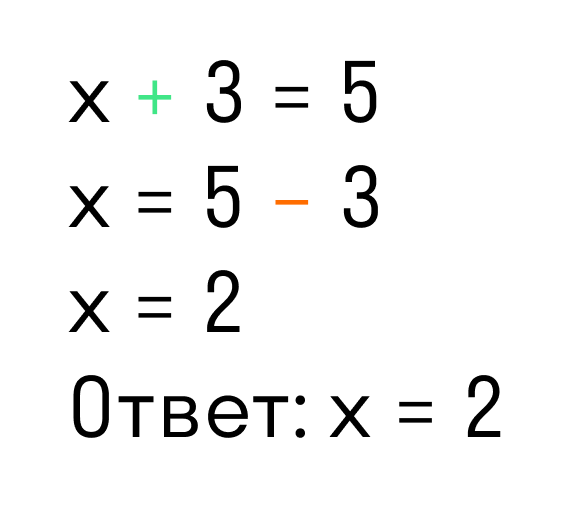Глобальный ответ на вопрос выполнить все расчеты и написать все уравнения

Видео:Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Глава 10. Решение вычислительных задач на компьютере

Практические работы

Видео:Химические уравнения - Как составлять уравнения реакций // Составление Уравнений Химических РеакцийСкачать

Практическая работа № 61.
Решение уравнений методом перебора

Напишите программу, которая находит все решения заданного вам уравнения на интервале [-5;5]. Программа должна выполнить следующие действия:

1. Определяет и выводит на экран интервалы, на которых расположены корни уравнения.

2. На каждом интервале, используя метод перебора, ищет решение с точностью 0,001 и выводит полученные решения на экран.

Вычисление функции, стоящей в левой части уравнения, оформите в виде подпрограммы.

Уровень A. Интервалы, на которых расположены корни, можно найти с помощью электронных таблиц. Программа запрашивает левую границу очередного интервала и выводит найденный корень уравнения.

Введите левую границу интервала:

Уровень B. Составить две программы, одна из которых выделяет все интервалы, на которых находятся корни, а вторая запрашивает левую границу очередного интервала и выводит найденный корень уравнения.

Уровень C. Составить одну программу, которая работает полностью автоматически: достаточно ввести в программу функцию и запустить. Программа находит все интервалы, на которых расположены корни и уточняет решения. После того, как очередной интервал найден, программа выводит его на экран и, применяя метод перебора с нужным шагом, уточняет решение.

Варианты заданий по теме «Решение уравнений»

Видео:НОВЫЙ ДЕТЕКТИВ ЛЮДМИЛЫ МАРТОВОЙ ВЛЮБИЛ В СЕБЯ ВСЕХ! Проклятие брачного договора. Все Серии Подряд!Скачать

Практическая работа № 62.
Решение уравнений методом деления отрезка пополам

Напишите программу, которая находит все решения заданного вам уравнения на интервале [-5;5]. Программа должна выполнить следующие действия:

1. Определяет и выводит на экран интервалы, на которых расположены корни уравнения.

2. Используя метод деления отрезка пополам, на каждом интервале ищет решение с точностью 0,001 и выводит полученные решения на экран.

Вычисление функции, стоящей в левой части уравнения, оформите в виде подпрограммы.

Уровень A. Интервалы, на которых расположены корни, можно найти с помощью электронных таблиц. Программа запрашивает границы очередного интервала и выводит найденный корень уравнения.

Введите границы интервала:

Уровень B. Составить две программы, одна из которых выделяет все интервалы, на которых находятся корни, а вторая запрашивает границы очередного интервала и выводит найденный корень уравнения, а также число шагов, которые потребовались для достижения заданной точности.

Введите границы интервала:

Уровень C. Составить одну программу, которая работает полностью автоматически: достаточно ввести в программу функцию и запустить. Программа находит все интервалы, на которых расположены корни и уточняет решения. После того, как очередной интервал найден, программа выводит его на экран и, применяя метод деления отрезка пополам, уточняет решение и определяет необходимое для этого количество шагов.

Видео:ВСЁ, что вы СТЕСНЯЛИСЬ СПРОСИТЬ про АВТО №3Скачать

Практическая работа № 63.
Решение уравнений в табличных процессорах

Уровень A. С помощью табличного процессора найдите все решения уравнения из примера «Полёт мяча», разобранного в учебнике.

Уровень B. Выполните задание уровня А. Затем выделите отдельную ячейку, в которой вычисляется максимальное значение функции на выбранном интервале. Используя эту ячейку и подбор параметра, найдите:

1) минимальную начальную скорость, при которой еще можно попасть в мишень;

2) максимальное расстояние, при котором можно попасть в мишень при начальной скорости 15 м/с.

Уровень C. Выполните задание уровня B. Затем, используя замену , постройте аналитическое решение уравнения из примера «Полёт мяча». Для практических вычислений используйте электронные таблицы. Сравните точное и численное решения.

Видео:Профессия, которую выбрали родители VS мечта VS реальность | ЕГЭ 2022 по физике | Снежа ПланкСкачать

Практическая работа № 64.
Вычисление длины кривой

Уровень A. Найдите длину параболы на интервале .

Уровень B. Для примера «Полет мяча» вычислите длину траектории движения шарика для углов вылета 35,5° и 65,8°. Сравните полученные результаты.

Уровень C. Постройте с помощью табличного процессора эллипс, который описывается уравнением при и . Напишите программу, которая вычисляет периметр этого эллипса с помощью дискретизации. Сравните ваш результат с тем, что получается по приближенной формуле Рамануджана: .

Экспериментально определите наибольший интервал дискретизации, при котором ошибка численного метода (в сравнении с результатом, полученным по формуле Рамануджана) составляет не более 1%.

Видео:Все о работе в Яндекс Еде. Ответ каналу Wylsacom.Скачать

Практическая работа № 65.
Вычисление площади фигуры

Уровень A. Найдите площадь фигуры, ограниченной параболой и осью OX, на интервале .

Уровень B. Найдите площадь фигуры, ограниченной графиками функций и .

Уровень C. Найдите площадь фигуры, ограниченной эллипсом

при и .

Сравните ваш результат с точным значением . Экспериментально определите наибольший интервал дискретизации, при котором ошибка численного метода составляет не более 1%.

Видео:ВСЕ ГРЕХИ И ЛЯПЫ игры "Atomic Heart" | ИгроГрехиСкачать

Практическая работа № 66.
Оптимизация. Метод дихотомии

Уровень A. Напишите программу, которая находит все минимумы и максимумы функции (см. варианты на следующей странице) на интервале [-5;5] с точностью 0,001, используя метод «золотого сечения». Границы интервала для поиска каждого минимума и максимума задаются вручную.

Уровень B. Напишите программу, которая находит все минимумы и максимумы функции (см. варианты на следующей странице) на интервале [-5;5] с точностью 0,001, используя метод «золотого сечения». Границы интервала для поиска каждого минимума и максимума определяются автоматически.

Уровень C. Напишите программу, которая находит все минимумы и максимумы функции (см. варианты на следующей странице) на интервале [-5;5] с точностью 0,001, используя метод «золотого сечения», причём на каждом шаге цикла вычисляется только одно новое значение функции. Границы интервала для поиска каждого минимума и максимума определяются автоматически.

Варианты заданий по теме «Оптимизация. Метод дихотомии»

max:(-1.612,14.703) min:( 1.612,-12.703)

max:(-0.565,12.715) min:( 2.348,-10.426)

max:( 0.368,11.753) min:( 2.760,-4.867)

max:(-2.210,19.058) min:( 0.857,-16.862)

max:(-2.520,12.001) min:( 0.250,-11.374)

max:(-0.527,17.584) min:( 2.115,-3.568)

max:(-2.754,21.186) min:( 0.604,-5.861)

max:(-2.601,30.604) min:( 0.691,-15.677)

max:(-2.986,27.177) min:( 0.187,-11.281)

max:(-2.987,21.011) min:( 1.072,-9.490)

max:(-3.417,15.758) min:( 0.072,-28.036)

max:(-3.314,27.161) min:( 0.361,-10.723)

max:(-2.208, 5.835) min:( 0.916,-6.647)

max:(-0.430,11.088) min:( 2.003,-6.333)

max:( 0.246,15.493) min:( 2.400,-2.049)

Видео:Вспоминаем все формулы ОГЭ по физике | Физика ОГЭ 2023 | УмскулСкачать

Практическая работа № 67.
Оптимизация с помощью табличных процессоров

Уровень A. В углах квадратного листа железа, сторона которого равна 1 м, вырезают четыре квадрата со стороной x. Затем складывают получившуюся развертку (по штриховым линиям на рисунке), сваривают швы и таким образом получается бак:

Определите размер выреза x, при котором получится бак наибольшего объема.

Уровень B. Выполните задание уровня А. Затем решите следующую задачу.

Фирма «Рога и копыта» хочет провести рекламную кампанию в газетах. Данные о цене рекламного объявления и тиражах газет внесены в таблицу:

В каждую газету нужно дать не менее одного и не более 6 объявлений. С помощью надстройки «Поиск решения» табличного процессора определите, сколько объявлений нужно дать в каждую газету, чтобы обеспечить общий охват не менее 200000 человек и при этом израсходовать как можно меньше денег.

Уровень C. Выполните задание уровня B. Затем решите следующую задачу[1].

Банка имеет форму цилиндра, размеры которого задаются радиусом и высотой . Площадь полной поверхности банки вычисляется как сумма площади боковой поверхности и площадей двух кругов-оснований. Решите следующие задачи:

1) найдите размеры банки, которая имеет максимальный объем при площади полной поверхности 100 см2;

2) найдите размеры банки, которая имеет минимальную площадь полной поверхности при объеме 500 см3.

Видео:Расчеты по уравнениям химических реакций. 1 часть. 8 класс.Скачать

Практическая работа № 68.
Статистические расчеты

В файле marks. xls вы найдете таблицу с оценками учеников по четырем предметам. Часть ее показана на рисунке:

1. С помощью табличного процессора определите:

· сколько пятерок, четверок и троек получено по каждому предмету;

· среднюю оценку по каждому предмету;

· средний балл каждого ученика

· стандартное отклонение оценок по каждому предмету от среднего значения.

2. Отсортируйте список учеников по убыванию среднего балла.

3. Найдите коэффициенты корреляции (взаимосвязь) между оценками по разным предметам, а также между средним баллом и оценками по каждому из предметов. Оформите данные в виде таблицы:

Оставьте у всех значений только три знака в дробной части.

Видео:Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Практическая работа № 69.
Условные вычисления

Уровень A. В файле salary. xls вы найдете таблицу расчета зарплаты работников фирмы «Рога и Копыта». Требуется добавить нужные формулы в столбцах Премия и Сумма.

Работник получает премию пропорционально перевыполнению плана. Например, если план выполнен на 120% (перевыполнение на 20%), размер премии составит 20% от его зарплаты. Работник, сделавший меньше нормы, не получает премии.

Уровень B. В файле olimp. xls вы найдете таблицу результатов районной олимпиады по математике. На городской тур проходят те учащиеся, которые набрали на районном туре не менее 10 баллов или решили полностью одну из самых сложных задач 6 или 7. За полное решение задач 1-4 дается 2 балла, задач 5-6 – 3 балла, задачи 7 – 4 балла.

1) Добавьте необходимые формулы в столбцы Сумма и Прошел. Нужно сделать так, чтобы проходной балл можно было легко менять в отдельной ячейке.

2) Определите, сколько участников прошли на городскую олимпиаду.

3) Постройте график, который показывает, как изменяется количество прошедших на городскую олимпиаду при изменении проходного балла.

Уровень C. Выполните работу уровня B. После этого выполните дополнительное задание:

4) *Было принято решение предоставить льготы девушкам: сделать для них проходной балл на 1 меньше, чем для юношей. Внесите размер этой льготы в отдельную ячейку и определите число прошедших на городскую олимпиаду с учетом льготы.

Видео:САМЫЙ ПРОСМАТРИВАЕМЫЙ ДЕТЕКТИВ ПРО ЛЮБИМУЮ ИНГУ ХВОСТИКОВУ! Три в одном. ВСЕ СЕЗОНЫ! Лучшие СериалыСкачать

Практическая работа № 70.
Метод наименьших квадратов

Уровень A. Для того, чтобы определить неизвестное сопротивление резистора R собрали электрическую схему, показанную на рисунке. Напряжение на резисторе регулируется с помощью реостата R­0 и измеряется вольтметром V. Сила тока в цепи измеряется амперметром A.

В текстовом файле mnk. txt результаты измерений записаны в два столбца: в первом столбце напряжение на проводнике, а во втором – соответствующая ему сила тока. Всего в файле 10 строчек с данными.

1) Напишите программу, которая читает данные из файла и вычисляет сопротивление резистора R, используя метод наименьших квадратов для закона Ома: .

2) Решите ту же задачу с помощью табличного процессора. Сравните результаты.

Уровень B. Выполните задание уровня А при условии, что точное количество измерений (количество строк с данными в файле) неизвестно, но не больше 100.

После этого решите задачу, решив задачу оптимизации в табличном процессоре. Для вычисления величины ошибки используйте функцию SUMXMY2 (СУММКВРАЗН). Сравните полученные результаты.

Уровень C. Выполните задание уровня B. Затем с помощью табличного процессора решите задачу двумя другими методами:

Метод 2. Используйте в качестве критерия оптимизации не сумму квадратов отклонений, а сумму абсолютных величин (модулей) этих отклонений. Для вычисления модуля примените стандартную функцию ABS.

Метод 3. Закон Ома можно записать в виде , где . Используя метод наименьших квадратов, найдите оптимальное значение с помощью своей программы и с помощью табличного процессора, а затем вычислите соответствующее значение .

Сравните результаты, полученные тремя методами. Какой из них вы рекомендуете использовать и почему?

Видео:Рекомендации по подготовке учащихся к выполнению заданий различного уровня сложности ЕГЭ по химииСкачать

Практическая работа № 71.
Линии тренда

Уровень A. Доходы начинающей фирмы (в тысячах рублей) за первые 5 лет работы приведены в таблице:

Видео:Формулы Excel – все особенности, тонкости и трюки в одном видео! - Функции Excel (2)Скачать

Хотите решить задачу онлайн? Получите ответ на любую задачу по математике с подробным решением за несколько секунд, например, как решить уравнение.

Видео:Решение номеров из второй части ОГЭ: Алгебраические выражения, уравнения, неравенстваСкачать

Pocket Teacher искусственный интеллект, который 30 лет разрабатывали в МГУ

Видео:Стрим #31 РАЗБОР ПОСЛЕДНЕГО ПРОБНИКАСкачать

Получите онлайн-помощника в решении множества математических дисциплин. Решить любую задачу, например решить уравнение очень просто!

• Иррациональные
• Рациональные
• Тригонометрические
• Логарифмические
• Экспоненциальные
• С произвольными параметрами
• Показательные произвольной сложности

• Определенные
• Неопределенные

• Геометрические задачи можно вводить в текстовом виде

• Подробное решение для дифференциальных уравнений
• Системы дифференциальных уравнений

• Матрицы — посчитать определитель
• Пределы — пока без подробного решения
• Текстовые математические задачи

Видео:Разбор всех типов 26-28 задач из сборника Добротина 2023 | Екатерина СтрогановаСкачать

Решайте задачи, заданные в текстовом виде

• Геометрии
• Физике скоро
• Химии скоро

Видео:Все расчётные задачи ЕГЭ по химии 2021 | ЛЕТНИЙ КУРССкачать

Pocket Teacher всегда под рукой

• мобильная версия

Видео:🔴 ЕГЭ-2023 по физике. Оформление расчетных задач с развёрнутым ответом (25-30)Скачать

Сервис будет полезен всем, кто сталкивается с математикой

• Проверит домашнее задание: решите задачи или уравнения и сравните результат
• Поможет разобраться в теме, которую вы пропустили или не поняли
• Поможет подготовиться к ЕГЭ

• Проверит решение ребенка
• Поможет решить задачу
• Сэкономит на репетиторе

• Поможет подготовиться к поступлению в ВУЗ и вспомнить пройденный материал
• Выручит на контрольной и экзамене
• Решит задачи из курсовой
• Сэкономит время на решении сложных задач на старших курсах
• Станет спасением для тех, у кого математика непрофильный предмет

Видео:Все реакции по теме «Хром» для ЕГЭ по химии | Екатерина СтрогановаСкачать

Pocket Teacher пользуются человек

Поступил в этом году на «вышку». Ваш сайт использовал для решения вступительных примеров и тестов. Всё понравилось! Четко, быстро и правильно. Спасибо! Буду использовать ваш ресурс и дальше, но уже в работе.

Нас всё устраивает. Ошибок в решениях выявлено не было. Приятный интерфейс. Решить уравнение очень просто и быстро.

Всё отлично работает, спасибо за помощь в решении сложных заданий! Решить задачу реально очень просто!

Очень удобный и полезный сервис. Очень устраивает! Спасибо!

Я пишу студентам научные работы, и использую ваш сайт для решения задач. Своим детям также решаю задачи и сложные примеры при помощи вашего сайта. Пока все разделы и интерфейс меня полностью устраивают.

Пока испробовал не все разделы сайта, но на данный момент меня все устраивает: быстро, правильно, профессионально.

Я являюсь мамой старшеклассника, и мой сын свято верит в то, что я могу решить по математике практически всё. Поэтому ваш сайт в данном случае меня прекрасно выручает! Никаких косяков как таковых не было!

С уважением, Ольга.

Благодарю за помощь, всё работает прекрасно! Очень благодарен разработчикам за такой сервис!

Видео:Распространенные заблуждения в программировании // Курс «Математика для программистов»Скачать

Решение простых линейных уравнений

О чем эта статья:

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядят так: ах + b = 0, где a и b — действительные числа. Вот, что поможет в решении:

если а ≠ 0 — уравнение имеет единственный корень: х = -b : а;

если а = 0 — уравнение корней не имеет;

если а и b равны нулю, то корнем уравнения является любое число.

Квадратное уравнение выглядит так: ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

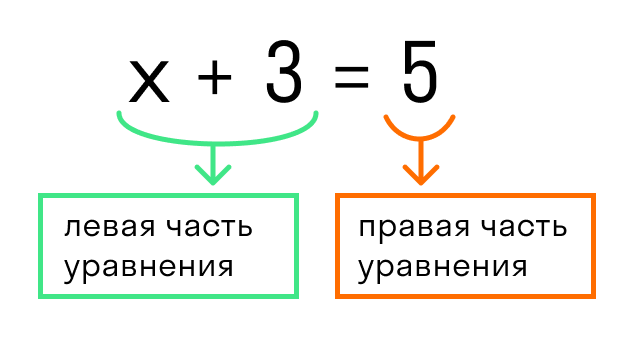
Для примера рассмотрим простейшее уравнение: x+3=5.

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

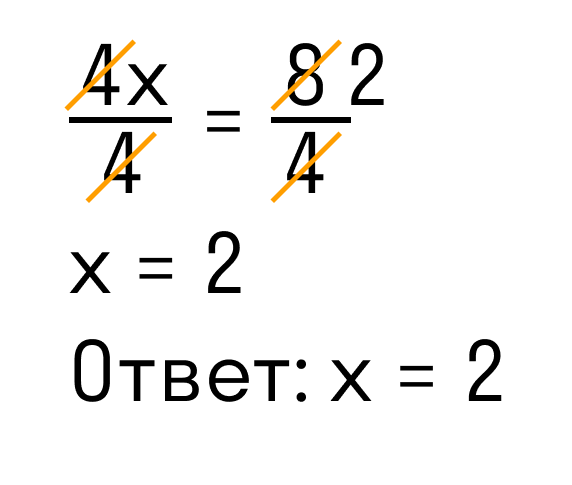
Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: -4x = 12

Разделим обе части на -4, чтобы коэффициент при неизвестной стал равен единице.

-4x = 12 | : (-4)
x = −3

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

ЮПеренести 1 из левой части в правую со знаком минус.

Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.

5х − 15 + 2 = 3х − 12 + 2х − 1

Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

5х − 3х − 2х = −12 − 1 + 15 − 2

Приведем подобные члены.

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

Пример 4. Решить: 4(х + 2) = 6 − 7х.