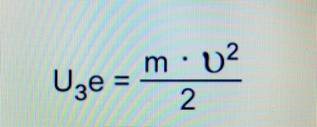Гипотеза планка о квантах фотоэффект опыты а г столетова уравнение эйнштейна для фотоэффекта фотон

Гипотеза Планка о квантах

Классическая электродинамика дала серьезный сбой, когда ее попытались использовать для описания излучения нагретого тела (так называемого теплового излучения).

Суть проблемы состояла в том, что простая и естественная электродинамическая модель теплового излучения приводила к бессмысленному выводу: любое нагретое тело, непрерывно излучая, должно постепенно потерять всю свою энергию и остыть до абсолютного нуля. Однако ничего подобного не наблюдается.

В ходе решения этой проблемы Макс Планк высказал свою знаменитую гипотезу.

Гипотеза о квантах. Электромагнитная энергия излучается и поглощается не непрерывно, а отдельными неделимыми порциями квантами. Энергия кванта пропорциональна частоте излучения:

C оотношение (1) называется формулой Планка, а коэффициент пропорциональности h — постоянной Планка.

Принятие этой гипотезы позволило Планку построить теорию теплового излучения, прекрасно согласующуюся с экспериментом. Располагая известными из опыта спектрами теплового излучения, Планк вычислил значение своей постоянной:

h = 6 , 63 * 10 — 34 Дж с ( 2 )

Успешность гипотезы Планка наводила на мысль, что законы классической физики неприменимы к малым частицам вроде атомов или электронов, а также к явлениям взаимодействия света и вещества. Подтверждением данной мысли как раз и послужило явление фотоэффекта.

Фотоэффект это выбивание электронов из вещества падающим светом. Явление фотоэффекта было открыто Генрихом Герцем в 1887 году в ходе его знаменитых экспериментов по излучению электромагнитных волн.

Герц, однако, был поглощен исследованием электромагнитных волн и не принял данный факт во внимание. Год спустя фотоэффект был независимо открыт русским физиком Александром Григорьевичем Столетовым. Тщательные экспериментальные исследования, проведенные Столетовым в течение двух лет, позволили сформулировать основные законы фотоэффекта.

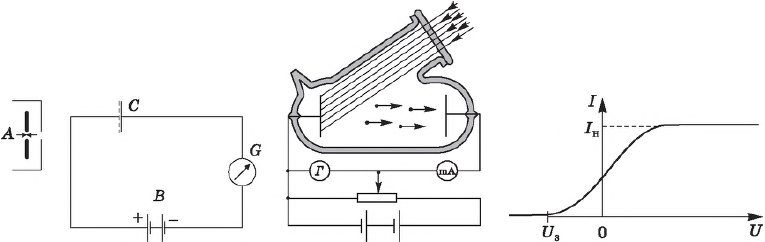
В своих экспериментах А.Г.Столетов использовал фотоэлемент собственной конструкции.

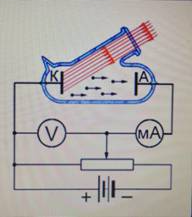
В стеклянную колбу, из которой выкачан воздух (чтобы не мешать лететь электронам), введены два электрода: цинковый катод K и анод A . На катод и анод подается напряжение, величину U которого можно менять с помощью потенциометра и измерять вольтметром V .

Сейчас к катоду подсоединен «минус», а аноду «плюс», но можно сделать и наоборот (и эта перемена знака существенная часть опытов Столетова). Напряжению на электродах приписывается тот знак, который подан на анод. В данном случае, например, напряжение U положительно.

Катод освещается ультрафиолетовыми лучами УФ через специальное кварцевое окошко, сделанное в колбе (стекло поглощает ультрафиолет, а кварц пропускает). Ультрафиолетовое излучение выбивает с катода электроны e , которые разгоняются напряжением U и летят на анод. Включенный в цепь миллиамперметр mA регистрирует электрический ток. Этот ток называется фототоком, а выбитые электроны, его создающие, называются фотоэлектронами.

В опытах Столетова можно независимо изменять три величины: анодное напряжение,

интенсивность света и его частоту.
Рис. 1. Фотоэлемент Столетова

З ависимость фототока от напряжения

Меняя величину и знак анодного напряжения, можно проследить, как меняется фототок. График этой зависимости, называемый характеристикой фотоэлемента, представлен на рис. 2.

Полученная кривая показывает, что электроны вылетают из катода с различными скоростями и в разных направлениях; максимальную скорость, которую имеют фотоэлектроны в условиях опыта, обозначим v .

Если напряжение U отрицательно и велико по модулю, то фототок отсутствует. Это легко понять: электрическое поле, действующее на электроны со стороны катода и анода, является тормозящим (на катоде «плюс», на аноде «минус») и обладает столь большой величиной, что электроны не в состоянии долететь до анода. Начального запаса кинетической энергии не хватает электроны теряют свою скорость на подступах к аноду и разворачиваются обратно на катод. Максимальная кинетическая энергия вылетевших электронов оказывается меньше, чем модуль работы поля при перемещении электрона с катода на анод: mv 2 /2 где m = 9,1*10 -31 кг — масса электрона,

e = — 1,6 10 -19 Кл — его заряд. Рис. 2 . Характеристика фотоэлемента

Будем постепенно увеличивать напряжение, т. е. двигаться слева направо вдоль оси U из отрицательных значений в положительные.

Поначалу тока по-прежнему нет, но точка разворота электронов становится все ближе к аноду. Наконец, при достижении напряжения U _з , которое называется задерживающим напряжением, электроны разворачиваются назад в момент достижения анода (иначе говоря, электроны прибывают на анод с нулевой скоростью). Имеем:

Таким образом, величина задерживающего напряжения позволяет определить максимальную кинетическую энергию фотоэлектронов.

При небольшом превышении задерживающего напряжения появляется слабый фототок. Его формируют электроны, вылетевшие с максимальной кинетической энергией почти точно вдоль оси колбы (т. е. почти перпендикулярно катоду): теперь электронам хватает этой энергии, чтобы добраться до анода с ненулевой скоростью и замкнуть цепь. Остальные электроны, которые имеют меньшие скорости или полетели в сторону от анода, на анод не попадают.

При повышении напряжения фототок увеличивается. Анода достигает большее количество электронов, вылетающих из катода под все большими углами к оси колбы. Обратите внимание, что фототок присутствует при нулевом напряжении!

Когда напряжение выходит в область положительных значений, фототок продолжает возрастать, т.к. электрическое поле теперь разгоняет электроны, поэтому все большее их число получают шанс оказаться на аноде. Однако достигают анода пока еще не все фотоэлектроны. Например, электрон, вылетевший с максимальной скоростью перпендикулярно оси колбы (т. е. вдоль катода), хоть и развернется полем в нужном направлении, но не настолько сильно, чтобы попасть на анод.

При достаточно больших положительных значениях напряжения ток достигает своей предельной величины I _н , называемой током насыщения, и дальше возрастать перестает — напряжение, ускоряющее электроны, становится настолько велико, что анод захватывает вообще все электроны, выбитые из катода в каком бы направлении и с какими бы скоростями они не начинали движение. Дальнейших возможностей увеличиваться у фототока нет.

Величина I _н тока насыщения — количество электронов, выбиваемых из катода за одну секунду. Будем менять интенсивность света, не трогая частоту. Опыт показывает, что ток насыщения меняется пропорционально интенсивности света.

Первый закон фотоэффекта: Число электронов, выбиваемых из катода за секунду, пропорционально интенсивности падающего на катод излучения (при его неизменной частоте).

Чем больше энергии несет излучение, тем ощутимее наблюдаемый результат.

Теперь будем изучать зависимость максимальной кинетической энергии фотоэлектронов от частоты и интенсивности падающего света. По формуле (3) нахождение максимальной кинетической энергии выбитых электронов фактически сводится к измерению задерживающего напряжения.

Сначала меняем частоту излучения при фиксированной интенсивности. Получается такой график (рис. 3):

Как видим, существует некоторая частота ν₀, называемая красной границей фотоэффекта, разделяющая две принципиально разные области графика. Если ν

Если же ν > ν ₀, то максимальная кинетическая энергия фотоэлектронов линейно растет с частотой.

Теперь, наоборот, фиксируем частоту и меняем интенсивность света. Если при этом ν ν₀: максимальная кинетическая энергия фотоэлектронов от интенсивности света не зависит.

Все эти факты нашли отражение во втором и третьем законах фотоэффекта. Рис. 3. Зависимость энергии

фотоэлектронов от частоты света

Второй закон фотоэффекта: Максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и не зависит от его интенсивности.

Третий закон фотоэффекта: Для каждого вещества существует красная граница фотоэффекта наименьшая частота света ν₀, при которой фотоэффект еще возможен. При ν

Видео:Физика 11 класс (Урок№22 - Фотоэффект.)Скачать

Квантовая физика. Изменение физических величин в процессах. Установление соответствия

Видео:Гипотеза Планка о световых квантах. Явление фотоэффекта.Скачать

Теория к заданию 21 из ЕГЭ по физике

Гипотеза Планка о квантах

Гипотеза Планка — предположение, что атомы испускают электромагнитную энергию (свет) не непрерывно, а отдельными порциями — квантами.

Энергия каждой порции пропорциональна частоте излучения:

где $h=6.63·10^$ $Дж·с$ — постоянная Планка, $ν$ — частота света.

Постоянная Планка (квант действия) — фундаментальная физическая константа. Введена М. Планком в 1900 г. Наиболее точное значение постоянной Планка $h = 6.626176(36) · 10^$ $Дж·с$. Чаще пользуются постоянной $h=/=1.0545887(57)·10^$ $Дж·с$, также называемой постоянной Планка. Формула $p↖=<mυ↖><√<1-/>$ — это вторая из простых великих формул физики (первая — формула Эйнштейна, связывающая энергию покоя тела с его массой). После открытия Планка начала развиваться квантовая теория.

Фотоны. Энергия и импульс фотона

Фотон (обозначение — $γ$) — элементарная частица, квант электромагнитного поля.

Развивая идею Планка об излучении электромагнитных волн квантами, А.Эйнштейн ввел гипотезу, согласно которой электромагнитное излучение само состоит из таких квантов, позднее названных фотонами.

Это свойство света было названо корпускулярным.

Масса покоя фотона равна нулю, следовательно, согласно СТО скорость его равна скорости света $с$, а энергия:

Из $E=hν=/=pc$ находим выражение для импульса:

Импульс фотона направлен по световому лучу. Чем больше частота, тем больше энергия и импульс фотона и тем отчетливее выражены корпускулярные свойства света.

Фотоэффект

Фотоэффект — испускание электронов веществом при поглощении им квантов электромагнитного излучения (фотонов).

Фотоэффект был открыт в 1887 г. Г. Герцем, который установил, что длина искры в разряднике увеличивается при попадании на его металлические электроды света от искры второго разрядника. Первые исследования фотоэффекта были выполнены русским ученым А. Г. Столетовым (1888 г.). Ф. Ленард и Дж. Томсон (1889 г.) доказали, что при фотоэффекте испускаются электроны.

Опыты Столетова. Законы фооэффекта

Схема опытов и прибор Столетова по наблюдению фотоэффекта представлены на рисунке. Здесь $С$ — два металлических диска, установленных параллельно друг другу (один — латунная или железная металлическая сетка, второй диск — сплошной). Диски соединены между собой проволокой, в которую введены гальваническая батарея $В$ и чувствительный гальванометр с большим сопротивлением ($5212$ Ом), $А$ — источник света (лампа с вольтовой дугой). Таким образом, две металлические пластины представляют собой конденсатор, причем металлическая сетка является положительной обкладкой конденсатора. Свет от дуги $А$ через сетку попадает на отрицательно заряженную сплошную металлическую пластину. Из опытов Столетова следовало, что фототок через гальванометр сильнее всего растет при освещении ультрафиолетовыми лучами, сила фототока пропорциональна интенсивности освещения, и под действием света освобождаются только отрицательные заряды.

При изучении фотоэффекта строят зависимость тока $I$ от напряжения $U$, подаваемого к электродам, один из которых (исследуемый фотокатод) освещается светом. Из полученной зависимости $I(U)$ следует, что при $U=0$ ток не равен нулю, а для того, чтобы ток стал равным нулю, необходимо подать некоторое напряжение обратной полярности (к освещенному электроду «+», к неосвещенному — «—»), которое называется задерживающим напряжением $U_з$ и определяется максимальной кинетической энергией вылетающих электронов: $/=eU_з$.

В процессе исследования фотоэффекта были установлены следующие закономерности.

1. Количество электронов, вырываемых светом с поверхности металла за $1$ с, прямо пропорционально поглощаемой за это время энергии световой волны.
2. Скорость электронов, вылетающих из тела при фотоэффекте, определяется его частотой $ν$ и не зависит от интенсивности.
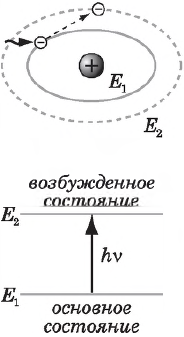
3. Для каждого вещества существует предельная наименьшая частота света $ν_$ (красная граница фотоэффекта), при которой возможен фотоэффект. Излучение с частотой $ν E_1$. Интенсивность поглощенного излучения пропорциональна концентрации $n_1$ атомов, находящихся в основном состоянии.

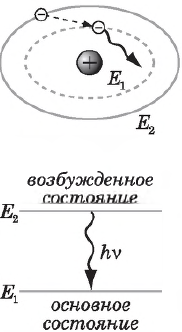
2. Спонтанное излучение. В отсутствие внешних полей или столкновений с другими частицами электрон, находящийся в возбужденном состоянии, через время порядка $10^-10^$
с спонтанно (самопроизвольно) возвращается в основное состояние, излучая фотон.

Спонтанное излучение — это излучение, испускаемое при самопроизвольном переходе атома из одного состояния в другое.

Спонтанное излучение различных атомов происходит некогерентно, т. к. каждый атом начинает и заканчивает излучать независимо от других.

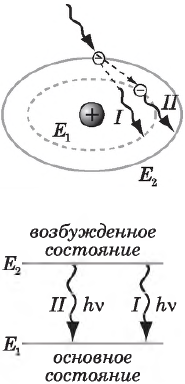
3. Индуцированное излучение. В 1917 г. Эйнштейн предсказал, что возбужденный атом может излучать под действием падающего на него света.

Индуцированное (вынужденное) излучение — излучение атома, возникающее при переходе на более низкий энергетический уровень под действием внешнего электромагнитного излучения.

Интенсивность индуцированного излучения пропорциональна концентрации щ атомов, находящихся в возбужденном состоянии. При этом световая волна, возникающая при индуцированном излучении, имеет ту же частоту, поляризацию, фазу и направление распространения, что и падающая на атом волна. Это означает, что интенсивность падающего излучения увеличивается, т. е. возникает оптическое усиление.

Принцип действия лазера

В 1939 г. российский физик В. А. Фабрикант наблюдал экспериментально усиление электромагнитных волн (оптическое усиление) в результате процесса индуцированного излучения. Российские ученые Н. Г. Басов и А. М. Прохоров и американский физик Ч. Таунс, создавшие в 1954 г. квантовый генератор излучения, работавший в сантиметровом диапазоне, были удостоены в 1964 г. Нобелевской премии по физике. Первый лазер, работающий на кристалле рубина в видимом диапазоне, был создан в 1960 г. американским физиком Т. Мейманом.

Усиление излучения, падающего на среду, будет происходить тогда, когда число частиц на возбужденном уровне $n_2$ превысит число частиц на основном уровне энергии: $n_2 > n_1$. Такое состояние системы называется инверсной населенностью. В состоянии термодинамического равновесия, когда система занимает основное состояние с наименьшей энергией $Е_1$, т. е. когда $n_1 > n_2$, усиления света не будет.

Инверсная населенность энергетических уровней — неравновесное состояние среды, при котором концентрация атомов в возбужденном состоянии больше, чем концентрация атомов в основном состоянии.

Однако спонтанные переходы препятствуют накоплению атомов в возбужденном состоянии. Этим можно пренебречь, если возбужденное состояние метастабильно.

Метастабильным называется возбужденное состояние электрона в атоме, в котором он может находиться гораздо дольше (например, $10^$ с), чем в обычном возбужденном состоянии ($10^$ с).

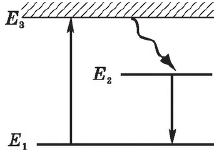
На этом основан принцип действия рубинового лазера. Рубин, используемый в качестве активного элемента в лазере, представляет собой монокристалл $А1_2O_3$, в котором часть ионов алюминия замещена ионами $Сг^$.

С помощью лампы-вспышки (оптической накачки) ионы хрома переводятся из основного состояния $Е_1$ в возбужденное — $Е_3$. Через $10^$ с ионы, передавая часть энергии кристаллической решетке, переходят из возбужденного состояния $Е_3$ в метастабильное состояние $Е_2 n_1$) этого уровня. Случайный фотон с энергией $hν=E_2-E_1$ может вызвать лавину индуцированных когерентных фотонов. Индуцированное излучение, распространяющееся вдоль оси цилиндрического монокристалла рубина, многократно отражается от его торцов и быстро усиливается.

Один из торцов рубинового стержня делают зеркальным, а другой — частично прозрачным. Через него выходит мощный импульс когерентного монохроматического излучения красного цвета с длиной волны $694.3$ нм.

В настоящее время существует много различных типов и конструкций лазеров.

Лазерное излучение обладает следующими особенностями:

1. исключительной монохроматичностью и когерентностью;
2. пучок света лазера имеет очень малый угол расхождения (около $10^$рад);
3. лазер — наиболее мощный искусственный источник света. Напряженность электрического поля в электромагнитной волне, излучаемой лазером, превышает напряженность поля внутри атома.

Состав ядра. Нуклонная модель Гейзенберга-Иваненко

Атомное ядро — это центральная часть атома, состоящая из протонов и нейтронов (которые вместе называются нуклонами).

Ядро было открыто Э. Резерфордом в 1911 г. при исследовании прохождения а-частиц через вещество. Оказалось, что почти вся масса атома ($99.95%$) сосредоточена в ядре. Размер атомного ядра имеет порядок величины $10^-10^$ см, что в $10 000$ раз меньше размера электронной оболочки.

Предложенная Э. Резерфордом планетарная модель атома и экспериментальное наблюдение им ядер водорода, выбитых $α$-частицами из ядер других элементов (1919—1920 гг.), привели ученого к представлению о протоне. Термин протон был введен в начале 20-х гг XX ст.

Протон (от protos — первый, символ $p$) — стабильная элементарная частица, ядро атома водорода.

Протон — положительно заряженная частица, заряд которой по абсолютной величине равен заряду электрона $e=1.6·10^$ Кл. Масса протона в $1836$ раз больше массы электрона. Масса покоя протона $m_p=1.6726231·10^кг=1.007276470 а.е.м.$

Второй частицей, входящей в состав ядра, является нейтрон.

Нейтрон (от лат. neuter — ни тот, ни другой, символ $n$) — это элементарная частица, не имеющая заряда, т. е. нейтральная.

Масса нейтрона в $1839$ раз превышает массу электрона. Масса нейтрона почти равна (незначительно больше) массе протона: масса покоя свободного нейтрона $m_n=1.6749286·10^кг=1.0008664902 а.е.м.$ и превосходит массу протона на $2.5$ массы электрона. Нейтрон, наряду с протоном под общим названием нуклон входит в состав атомных ядер.

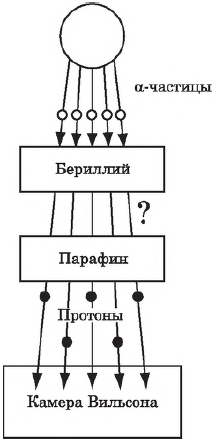
Нейтрон был открыт в 1932 г. учеником Э. Резерфорда Д. Чедвигом при бомбардировке бериллия $α$-частицами. Возникающее при этом излучение с большой проникающей способностью (преодолевало преграду из свинцовой пластины толщиной $10-20$ см) усиливало свое действие при прохождении через парафиновую пластину. Оценка энергии этих частиц по трекам в камере Вильсона, сделанная супругами Жолио-Кюри, и дополнительные наблюдения позволили исключить первоначальное предположение о том, что это $γ$-кванты. Большая проникающая способность новых частиц, названных нейтронами, объяснялась их электронейтральностью. Ведь заряженные частицы активно взаимодействуют с веществом и быстро теряют свою энергию. Существование нейтронов было предсказано Э. Резерфордом за 10 лет до опытов Д. Чедвига. При попадании $α$-частиц в ядра бериллия происходит следующая реакция:

Здесь $↙↖n$ — символ нейтрона; заряд его равен нулю, а относительная атомная масса приблизительно равна единице. Нейтрон — нестабильная частица: свободный нейтрон за время $

15$ мин. распадается на протон, электрон и нейтрино — частицу, лишенную массы покоя.

После открытия Дж. Чедвиком нейтрона в 1932 г. Д. Иваненко и В. Гейзенберг независимо друг от друга предложили протоннонейтронную (нуклонную) модель ядра. Согласно этой модели, ядро состоит из протонов и нейтронов. Число протонов $Z$ совпадает с порядковым номером элемента в таблице Д. И. Менделеева.

Заряд ядра $Q$ определяется числом протонов $Z$, входящих в состав ядра, и кратен абсолютной величине заряда электрона $e$:

Число $Z$ называется зарядовым числом ядра или атомным номером.

Массовым числом ядра $А$ называется общее число нуклонов, т. е. протонов и нейтронов, содержащихся в нем. Число нейтронов в ядре обозначается буквой $N$. Таким образом, массовое число равно:

Нуклонам (протону и нейтрону) приписывается массовое число, равное единице, электрону — нулевое значение.

Представлению о составе ядра содействовало также открытие изотопов.

Изотопы (от греч. isos — равный, одинаковый и topos — место) — это разновидности атомов одного и того же химического элемента, атомные ядра которых имеют одинаковое число протонов ($Z$) и различное число нейтронов ($N$).

Изотопами называются также ядра таких атомов. Изотопы являются нуклидами одного элемента. Нуклид (от лат. nucleus — ядро) — любое атомное ядро (соответственно атом) с заданными числами $Z$ и $N$. Общее обозначение нуклидов имеет вид $↙↖X_N$, где $X$ — символ химического элемента, $A=Z+N$ — массовое число.

Изотопы занимают одно и то же место в Периодической системе элементов, откуда и произошло их название. По своим ядерным свойствам (например, по способности вступать в ядерные реакции) изотопы, как правило, существенно отличаются. Химические (и почти в той же мере физические) свойства изотопов одинаковы. Это объясняется тем, что химические свойства элемента определяются зарядом ядра, поскольку именно он влияет на структуру электронной оболочки атома.

Исключением являются изотопы легких элементов. Изотопы водорода $↖H$ — протий, $↖H$ — дейтерий, $↖H$ — тритий столь сильно отличаются по массе, что и их физические и химические свойства различны. Дейтерий стабилен (т. е. не радиоактивен) и входит в качестве небольшой примеси ($1:4500$) в обычный водород. При соединении дейтерия с кислородом образуется тяжелая вода. Она при нормальном атмосферном давлении кипит при $101.2°$С и замерзает при $+3.8°$С. Тритий $β$-радиоактивен с периодом полураспада около $12$ лет.

У всех химических элементов имеются изотопы. У некоторых элементов имеются только нестабильные (радиоактивные) изотопы. Для всех элементов искусственно получены радиоактивные изотопы.

Изотопы урана. У элемента урана есть два изотопа — с массовыми числами $235$ и $238$. Изотоп $↙↖U$ составляет всего $/$ часть от более распространенного $↙↖U$.

Энергия связи нуклонов в ядре. Ядерные силы

Поскольку протоны в ядре имеют одинаковый положительный заряд, они отталкиваются. Для того чтобы удержать их вместе, должны существовать силы, намного превышающие силы электрического и гравитационного взаимодействия. Эти силы называются ядерными силами. Они в $100$ раз превосходят электрические (кулоновские) силы. Это самые мощные силы из всех, которыми располагает природа. Поэтому взаимодействие ядерных частиц относят к сильным взаимодействиям — особому типу взаимодействия, присущему большинству элементарных частиц наряду с электромагнитными взаимодействиями. Ядерные силы заметно проявляются лишь на расстояниях порядка $10^-10^$ см, равных по порядку величины размерам ядра, что показали опыты Резерфорда по рассеянию $α$-частиц ядрами.

Устойчивость атомного ядра характеризуется энергией связи ($Е_$). Энергия связи — это энергия, которую надо затратить, чтобы расщепить ядро. Ее принято выражать в мегаэлектронвольтах (МэВ) ($1 МэВ = 1.6·10^Дж$).

Под энергией связи ядра понимают ту энергию, которая необходима для полного расщепления ядра на отдельные нуклоны. На основании закона сохранения энергии можно также утверждать, что энергия связи равна той энергии, которая выделяется при образовании ядра из отдельных частиц. Энергия связи атомных ядер очень велика. Определить ее можно, применяя соотношение Эйнштейна между массой и энергией: $E=mc^2$.

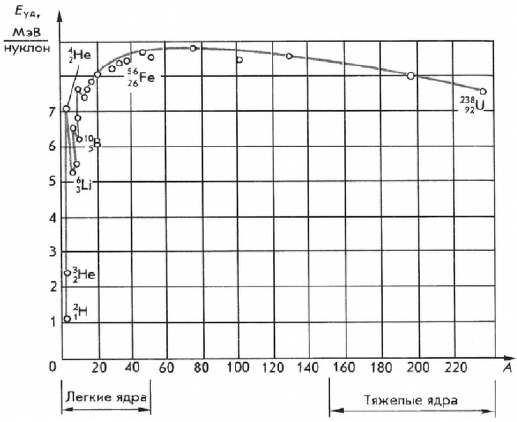
Удельной энергией связи называют энергию связи, приходящуюся на один нуклон ядра. Ее определяют экспериментально. Зависимость $Е_$ от массового числа $А$ приведена на рисунке. Как видно из рисунка, удельная энергия связи примерно постоянна (не считая самых легких ядер) и равна $8$ МэВ/нуклон. Слабый максимум ($8.6$ МэВ) приходится на элементы с массовыми числами от $50$ до $60$, т. е. на железо и близкие к нему по порядковому номеру элементы. Ядра этих элементов наиболее устойчивы.

У тяжелых ядер удельная энергия связи уменьшается за счет растущей с увеличением $Z$ кулоновской энергии отталкивания протонов. Кулоновские силы стремятся разорвать ядро.

Дефект массы

Точнейшие измерения показывают, что масса покоя ядра $М_я$ всегда меньше суммы масс покоя составляющих ее протонов и нейтронов: $М_я 100$.

Деление ядер урана было обнаружено в 1939 г. Ганом и Штрасманом, которые однозначно доказали, что при бомбардировке нейтронами ядер урана $U$ появляются радиоактивные ядра с массами и зарядами, примерно в два раза меньшими, чем масса и заряд ядра $U$. В том же году Л. Мейтнер и О. Фриш ввели термин «деление ядер» и отметили, что при этом выделяется огромная энергия, а Ф. Жолио-Кюри и Э. Ферми одновременно обнаружили, что при делении происходит испускание нескольких нейтронов (нейтроны деления). На основании этого была выдвинута идея самоподдерживающейся цепной реакции деления и использования деления ядер в качестве источника энергии. Основой современной ядерной энергетики служит деление ядер $↙↖U$ и $↖Pu$ поддействиемнейтронов.

Деление ядра возможно благодаря тому, что масса покоя тяжелого ядра больше суммы масс покоя осколков, возникающих при делении. Такой процесс энергетически выгоден.

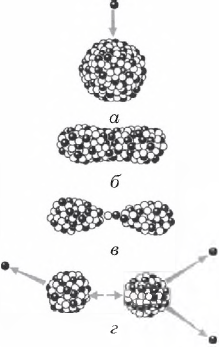
Механизм деления ядра объясняется на основе капельной модели, согласно которой сгусток нуклонов напоминает капельку заряженной жидкости. Ядро удерживают от распада ядерные силы притяжения, большие, чем силы кулоновского отталкивания, действующие между протонами и стремящиеся разорвать ядро.

Ядро $↙↖U$ имеет форму шара. После поглощения нейтрона оно возбуждается и деформируется, приобретая вытянутую форму, и растягивается до тех пор, пока силы отталкивания между половинками вытянутого ядра не станут больше сил притяжения, действующих в перешейке. После этого ядро разрывается на две части. Осколки под действием кулоновских сил отталкивания разлетаются со скоростью, равной $/$ скорости света.

Испускание нейтронов в процессе деления, о котором говорилось выше, объясняется тем, что относительное число нейтронов (по отношению к числу протонов) в ядре растет с увеличением атомного номера, и для образовавшихся при делении осколков число нейтронов оказывается большим, чем это допустимо для ядер атомов с меньшими номерами. г

Деление обычно происходит на осколки неравной массы. Эти осколки радиоактивны. После серии $β$-распадов в конце концов получаются стабильные ионы.

Кроме вынужденного, описанного выше, существует и спонтанное деление ядер урана, открытое в 1940 г. советскими физиками Г. Н. Флеровым и К. А. Петржаком. Период полураспада для спонтанного деления равен $10^$ лет, что в два миллиона раз больше периода полураспада при $α$-распаде урана.

Синтез ядер осуществляется в термоядерных реакциях. Термоядерные реакции — это реакции слияния легких ядер при очень высокой температуре. Выделяющаяся при слиянии (синтезе) энергия оказывается наибольшей при синтезе легких элементов, обладающих минимальной энергией связи. При соединении двух легких ядер, например, дейтерия и трития, образуется более тяжелое яро гелия с большей энергией связи:

При таком процессе ядерного синтеза выделяется значительная энергия ($17.6$ Мэв), равная разности энергий связи тяжелого ядра $↙↖Не$ и двух легких ядер $↙↖Н$ и $↙↖Н$. Образующийся при реакциях нейтрон приобретает $70%$ этой энергии. Сравнение энергии, приходящейся на один нуклон в реакциях ядерного деления ($0.9$ Мэв) и синтеза ($17.6$ Мэв), показывает, что реакция синтеза легких ядер энергетически более выгодна, чем реакция деления тяжелых.

Слияние ядер происходит под действием сил ядерного притяжения, поэтому они должны сблизиться до расстояний, меньших $10^$ м, на которых действуют ядерные силы. Этому сближению препятствует кулоновское отталкивание положительно заряженных ядер. Оно может быть преодолено только за счет большой кинетической энергии ядер, превышающей энергию их кулоновского отталкивания. Соответствующие расчеты показывают, что кинетическая энергия ядер, необходимая для реакции синтеза, может быть достигнута при температурах порядка сотен миллионов градусов, поэтому эти реакции называются термоядерными.

Термоядерный синтез — реакция, в которой при высокой температуре, большей $107$ К, из легких ядер синтезируются более тяжелые.

Термоядерный синтез — источник энергии всех звезд, в том числе, и Солнца.

Основным процессом, при котором происходит освобождение термоядерной энергии в звездах, является превращение водорода в гелий. За счет дефекта массы в этой реакции масса Солнца уменьшается каждую секунду на $4$ млн тонн.

Большую кинетическую энергию, необходимую для термоядерного синтеза, ядра водорода получают в результате сильного гравитационного притяжения к центру звезды. Затем при слиянии ядер гелия образуются и более тяжелые элементы.

Термоядерные реакции играют решающую роль в эволюции химического состава вещества во Вселенной. Все эти реакции сопровождаются выделением энергии, излучаемой звездами в виде света на протяжении миллиардов лет.

Осуществление управляемого термоядерного синтеза предоставило бы человечеству новый, практически неисчерпаемый источник энергии. И дейтерий, и тритий, необходимые для его осуществления, вполне доступны. Первый содержится в воде морей и океанов (в количестве, достаточном для использования в течение миллиона лет), второй может быть получен в ядерном реакторе при облучении жидкого лития (запасы которого огромны) нейтронами:

Одним из важнейших преимуществ управляемого термоядерного синтеза является отсутствие радиоактивных отходов при его осуществлении (в отличие от реакций деления тяжелых ядер урана).

Главным препятствием на пути осуществления управляемого термоядерного синтеза является невозможность удержания высокотемпературной плазмы с помощью сильных магнитных полей в течение $0.1-1$ с. Однако существует уверенность в том, что рано или поздно термоядерные реакторы будут созданы.

Пока же удалось осуществить лишь неуправляемую реакцию синтеза взрывного типа в водородной бомбе.

Цепные ядерные реакции

Ядерные цепные реакции — это ядерные реакции, в которых частицы, вызывающие их, образуются и как продукты этих реакций. Такой реакцией является деление урана и некоторых трансурановых элементов (например, $↖Рu$) под действием нейтронов. Впервые она была осуществлена Э. Ферми в 1942 г. После открытия деления ядер У. Зинн, Л. Силард и Г. Н. Флеров показали, что при делении ядра урана $U$ вылетает больше одного нейтрона: $n+U→A+B+ν$. Здесь $А$ и $В$ — осколки деления с массовыми числами $А$ от $90$ до $150$, $ν$ — число вторичных нейтронов.

Коэффициент размножения нейтронов. Для течения цепной реакции необходимо, чтобы среднее число освобожденных нейтронов в данной массе урана не уменьшалось со временем, или чтобы коэффициент размножения нейтронов $k$ был больше или равен единице.

Коэффициентом размножения нейтронов называют отношение числа нейтронов в каком-либо поколении к числу нейтронов предшествующего поколения. Под сменой поколений понимают деление ядер, при котором поглощаются нейтроны старого поколения и рождаются новые нейтроны.

Если $k≥1$, то число нейтронов увеличивается с течением времени или остается постоянным, и цепная реакция идет. При $k

Видео:Урок 434. Фотоэффект. Законы фотоэффектаСкачать

Фотоэффект

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: гипотеза М.Планка о квантах, фотоэффект, опыты А.Г.Столетова, уравнение Эйнштейна для фотоэффекта.

Фотоэффект — это выбивание электронов из вещества падающим светом. Явление фотоэффекта было открыто Генрихом Герцем в 1887 году в ходе его знаменитых экспериментов по излучению электромагнитных волн.
Напомним, что Герц использовал специальный разрядник (вибратор Герца) — разрезанный пополам стержень с парой металлических шариков на концах разреза. На стержень подавалось высокое напряжение, и в промежутке между шариками проскакивала искра. Так вот, Герц обнаружил, что при облучении отрицательно заряженного шарика ультрафиолетовым светом проскакивание искры облегчалось.

Герц, однако, был поглощён исследованием электромагнитных волн и не принял данный факт во внимание. Год спустя фотоэффект был независимо открыт русским физиком Александром Григорьевичем Столетовым. Тщательные экспериментальные исследования, проведённые Столетовым в течение двух лет, позволили сформулировать основные законы фотоэффекта.

Видео:ФОТОЭФФЕКТ И УРАВНЕНИЕ ЭЙНШТЕЙНА НА ПРИМЕРЕ ТЮРЬМЫСкачать

Опыты Столетова

В своих знаменитых экспериментах Столетов использовал фотоэлемент собственной конструкции (Фотоэлементом называется любое устройство, позволяющее наблюдать фотоэффект). Его схема изображена на рис. 1 .

Рис. 1. Фотоэлемент Столетова

В стеклянную колбу, из которой выкачан воздух (чтобы не мешать лететь электронам), введены два электрода: цинковый катод и анод . На катод и анод подаётся напряжение, величину которого можно менять с помощью потенциометра и измерять вольтметром .

Сейчас на катод подан «минус», а на анод — «плюс», но можно сделать и наоборот (и эта перемена знака — существенная часть опытов Столетова). Напряжению на электродах приписывается тот знак, который подан на анод (Поэтому поданное на электроды напряжение часто называют анодным напряжением). В данном случае, например, напряжение положительно.

Катод освещается ультрафиолетовыми лучами УФ через специальное кварцевое окошко, сделанное в колбе (стекло поглощает ультрафиолет, а кварц пропускает). Ультрафиолетовое излучение выбивает с катода электроны , которые разгоняются напряжением и летят на анод. Включённый в цепь миллиамперметр регистрирует электрический ток. Этот ток называется фототоком, а выбитые электроны, его создающие, называются фотоэлектронами.

В опытах Столетова можно независимо варьировать три величины: анодное напряжение, интенсивность света и его частоту.

Видео:ФОТОЭФФЕКТ. Гипотеза Планка. Уравнений Эйнштейна. ЕГЭ по Физике 2021. Николай НьютонСкачать

Зависимость фототока от напряжения

Меняя величину и знак анодного напряжения, можно проследить, как меняется фототок. График этой зависимости, называемый характеристикой фотоэлемента, представлен на рис. 2 .

Рис. 2. Характеристика фотоэлемента

Давайте обсудим ход полученной кривой. Прежде всего заметим, что электроны вылетают из катода с различными скоростями и в разных направлениях; максимальную скорость, которую имеют фотоэлектроны в условиях опыта, обозначим .

Если напряжение отрицательно и велико по модулю, то фототок отсутствует. Это легко понять: электрическое поле, действующее на электроны со стороны катода и анода, является тормозящим (на катоде «плюс», на аноде «минус») и обладает столь большой величиной, что электроны не в состоянии долететь до анода. Начального запаса кинетической энергии не хватает — электроны теряют свою скорость на подступах к аноду и разворачиваются обратно на катод. Максимальная кинетическая энергия вылетевших электронов оказывается меньше, чем модуль работы поля при перемещении электрона с катода на анод:

Здесь кг — масса электрона, Кл — его заряд.

Будем постепенно увеличивать напряжение, т.е. двигаться слева направо вдоль оси из далёких отрицательных значений.

Поначалу тока по-прежнему нет, но точка разворота электронов становится всё ближе к аноду. Наконец, при достижении напряжения , которое называется задерживающим напряжением, электроны разворачиваются назад в момент достижения анода (иначе говоря, электроны прибывают на анод с нулевой скоростью). Имеем:

Таким образом, величина задерживающего напряжения позволяет определить максимальную кинетическую энергию фотоэлектронов.

При небольшом превышении задерживающего напряжения появляется слабый фототок. Его формируют электроны, вылетевшие с максимальной кинетической энергией почти точно вдоль оси колбы (т.е. почти перпендикулярно катоду): теперь электронам хватает этой энергии, чтобы добраться до анода с ненулевой скоростью и замкнуть цепь. Остальные электроны, которые имеют меньшие скорости или полетели в сторону от анода, на анод не попадают.

При повышении напряжения фототок увеличивается. Анода достигает большее количество электронов, вылетающих из катода под всё большими углами к оси колбы. Обратите внимание, что фототок присутствует при нулевом напряжении!

Когда напряжение выходит в область положительных значений, фототок продолжает возрастать. Оно и понятно: электрическое поле теперь разгоняет электроны, поэтому всё большее их число получают шанс оказаться на аноде. Однако достигают анода пока ещё не все фотоэлектроны. Например, электрон, вылетевший с максимальной скоростью перпендикулярно оси колбы (т.е. вдоль катода), хоть и развернётся полем в нужном направлении, но не настолько сильно, чтобы попасть на анод.

Наконец, при достаточно больших положительных значениях напряжения ток достигает своей предельной величины , называемой током насыщения, и дальше возрастать перестаёт.

Почему? Дело в том, что напряжение, ускоряющее электроны, становится настолько велико, что анод захватывает вообще все электроны, выбитые из катода — в каком бы направлении и с какими бы скоростями они не начинали движение. Стало быть, дальнейших возможностей увеличиваться у фототока попросту нет — ресурс, так сказать, исчерпан.

Видео:Фотоэффект. Гипотеза Планка. Подготовка к ЕГЭ по физике | Николай Ньютон. ТехноскулСкачать

Законы фотоэффекта

Величина тока насыщения — это, по существу, количество электронов, выбиваемых из катода за одну секунду. Будем менять интенсивность света, не трогая частоту. Опыт показывает, что ток насыщения меняется пропорционально интенсивности света.

Первый закон фотоэффекта. Число электронов, выбиваемых из катода за секунду, пропорционально интенсивности падающего на катод излучения (при его неизменной частоте).

Ничего неожиданного в этом нет: чем больше энергии несёт излучение, тем ощутимее наблюдаемый результат. Загадки начинаются дальше.

А именно, будем изучать зависимость максимальной кинетической энергии фотоэлектронов от частоты и интенсивности падающего света. Сделать это несложно: ведь в силу формулы (1) нахождение максимальной кинетической энергии выбитых электронов фактически сводится к измерению задерживающего напряжения.

Сначала меняем частоту излучения при фиксированной интенсивности. Получается такой график (рис. 3 ):

Рис. 3. Зависимость энергии фотоэлектронов от частоты света

Как видим, существует некоторая частота , называемая красной границей фотоэффекта, разделяющая две принципиально разные области графика. Если , то фотоэффекта нет.

Если же nu_0′ alt=’nu > nu_0′ /> , то максимальная кинетическая энергия фотоэлектронов линейно растёт с частотой.

Теперь, наоборот, фиксируем частоту и меняем интенсивность света. Если при этом , то фотоэффект не возникает, какова бы ни была интенсивность! Не менее удивительный факт обнаруживается и при nu_0′ alt=’nu > nu_0′ /> : максимальная кинетическая энергия фотоэлектронов от интенсивности света не зависит.

Все эти факты нашли отражение во втором и третьем законах фотоэффекта.

Второй закон фотоэффекта. Максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и не зависит от его интенсивности.

Третий закон фотоэффекта. Для каждого вещества существует красная граница фотоэффекта — наименьшая частота света , при которой фотоэффект ещё возможен. При фотоэффект не наблюдается ни при какой интенсивности света.

Видео:законы Столетова Уравнение Эйнштейна для внешнего фотоэффектаСкачать

Трудности классического объяснения фотоэффекта

Как можно было бы объяснить фотоэффект с точки зрения классической электродинамики и волновых представлений о свете?

Известно, что для вырывания электрона из вещества требуется сообщить ему некоторую энергию , называемую работой выхода электрона. В случае свободного электрона в металле это работа по преодолению поля положительных ионов кристаллической решётки, удерживающего электрон на границе металла. В случае электрона, находящегося в атоме, работа выхода есть работа по разрыву связи электрона с ядром.

В переменном электрическом поле световой волны электрон начинает совершать колебания.

И если энергия колебаний превысит работу выхода, то электрон будет вырван из вещества.

Однако в рамках таких представлений невозможно понять второй и третий законы фотоэффекта. Действительно, почему кинетическая энергия выбитых электронов не зависит от интенсивности излучения? Ведь чем больше интенсивность, тем больше напряжённость электрического поля в электромагнитной волне, тем больше сила, действующая на электрон, тем больше энергия его колебаний и с тем большей кинетической энергией электрон вылетит из катода. Логично? Логично. Но эксперимент показывает иное.

Далее, откуда берётся красная граница фотоэффекта? Чем «провинились» низкие частоты? Казалось бы, с ростом интенсивности света растёт и сила, действующая на электроны; поэтому даже при низкой частоте света электрон рано или поздно будет вырван из вещества — когда интенсивность достигнет достаточно большого значения. Однако красная граница ставит жёсткий запрет на вылет электронов при низких частотах падающего излучения.

Кроме того, неясна безынерционность фотоэффекта. Именно, при освещении катода излучением сколь угодно слабой интенсивности (с частотой выше красной границы) фотоэффект начинается мгновенно — в момент включения освещения. Между тем, казалось бы, электронам требуется некоторое время для «расшатывания» связей, удерживающих их в веществе, и это время «раскачки» должно быть тем больше, чем слабее падающий свет. Аналогия такая: чем слабее вы толкаете качели, тем дольше придётся их раскачивать до заданной амплитуды.

Выглядит опять-таки логично, но опыт — единственный критерий истины в физике! — этим доводам противоречит.

Так на рубеже XIX и XX столетий в физике возникла тупиковая ситуация: электродинамика, предсказавшая существование электромагнитных волн и великолепно работающая в диапазоне радиоволн, отказалась объяснять явление фотоэффекта.

Выход из этого тупика был найден Альбертом Эйнштейном в 1905 году. Он нашёл простое уравнение, описывающее фотоэффект. Все три закона фотоэффекта оказались следствиями уравнения Эйнштейна.

Главная заслуга Эйнштейна состояла в отказе от попыток истолковать фотоэффект с позиций классической электродинамики. Эйнштейн привлёк к делу смелую гипотезу о квантах, высказанную Максом Планком пятью годами ранее.

Видео:Опыты Столетова. Законы фотоэффекта. Уравнение ЭйнштейнаСкачать

Гипотеза Планка о квантах

Классическая электродинамика отказалась работать не только в области фотоэффекта. Она также дала серьёзный сбой, когда её попытались использовать для описания излучения нагретого тела (так называемого теплового излучения).

Суть проблемы состояла в том, что простая и естественная электродинамическая модель теплового излучения приводила к бессмысленному выводу: любое нагретое тело, непрерывно излучая, должно постепенно потерять всю свою энергию и остыть до абсолютного нуля. Как мы прекрасно знаем, ничего подобного не наблюдается.

В ходе решения этой проблемы Макс Планк высказал свою знаменитую гипотезу.

Гипотеза о квантах. Электромагнитная энергия излучается и поглощается не непрерывно, а отдельными неделимыми порциями — квантами. Энергия кванта пропорциональна частоте излучения:

Cоотношение (2) называется формулой Планка, а коэффициент пропорциональности — постоянной Планка.

Принятие этой гипотезы позволило Планку построить теорию теплового излучения, прекрасно согласующуюся с экспериментом. Располагая известными из опыта спектрами теплового излучения, Планк вычислил значение своей постоянной:

Успешность гипотезы Планка наводила на мысль, что законы классической физики неприменимы к малым частицам вроде атомов или электронов, а также к явлениям взаимодействия света и вещества. Подтверждением данной мысли как раз и послужило явление фотоэффекта.

Видео:Физика - Внешний фотоэлектрический эффект. уравнение Эйнштейна для фотоэффектаСкачать

Уравнение Эйнштейна для фотоэффекта

Гипотеза Планка говорила о дискретности излучения и поглощения электромагнитных волн, то есть о прерывистом характере взаимодействия света с веществом. При этом Планк считал, что распространение света — это непрерывный процесс, происходящий в полном соответствии с законами классической электродинамики.

Эйнштейн пошёл ещё дальше: он предположил, что свет в принципе обладает прерывистой структурой: не только излучение и поглощение, но также и распространение света происходит отдельными порциями — квантами, обладающими энергией .

Планк рассматривал свою гипотезу лишь как математический трюк и не решился опровергнуть электродинамику применительно к микромиру. Физической реальностью кванты стали благодаря Эйнштейну.

Кванты электромагнитного излучения (в частности, кванты света) стали впоследствии называться фотонами. Таким образом, свет состоит из особых частиц — фотонов, движущихся в вакууме со скоростью .

Каждый фотон монохроматического света, имеющего частоту , несёт энергию .

Фотоны могут обмениваться энергией и импульсом с частицами вещества (об импульсе фотона речь пойдёт в следующем листке); в таком случае мы говорим о столкновении фотона и частицы. В частности, происходит столкновение фотонов с электронами металла катода.

Поглощение света — это поглощение фотонов, то есть неупругое столкновение фотонов с частицами (атомами, электронами). Поглощаясь при столкновении с электроном, фотон передаёт ему свою энергию. В результате электрон получает кинетическую энергию мгновенно, а не постепенно, и именно этим объясняется безынерционность фотоэффекта.

Уравнение Эйнштейна для фотоэффекта есть не что иное, как закон сохранения энергии. На что идёт энергия фотона ? при его неупругом столкновении с электроном? Она расходуется на совершение работы выхода по извлечению электрона из вещества и на придание электрону кинетической энергии :

Слагаемое оказывается максимальной кинетической энергией фотоэлектронов. Почему максимальной? Этот вопрос требует небольшого пояснения.

Электроны в металле могут быть свободными и связанными. Свободные электроны «гуляют» по всему металлу, связанные электроны «сидят» внутри своих атомов. Кроме того, электрон может находиться как вблизи поверхности металла, так и в его глубине.

Ясно, что максимальная кинетическая энергия фотоэлектрона получится в том случае, когда фотон попадёт на свободный электрон в поверхностном слое металла — тогда для выбивания электрона достаточно одной лишь работы выхода.

Во всех других случаях придётся затрачивать дополнительную энергию — на вырывание связанного электрона из атома или на «протаскивание» глубинного электрона к поверхности.

Эти лишние затраты приведут к тому, что кинетическая энергия вылетевшего электрона окажется меньше.

Замечательное по простоте и физической ясности уравнение (4) содержит в себе всю теорию фотоэффекта. Давайте посмотрим, какое объяснение получают законы фотоэффекта с точки зрения уравнения Эйнштейна.

1. Число выбиваемых электронов пропорционально числу поглощённых фотонов. С увеличением интенсивности света количество фотонов, падающих на катод за секунду, возрастает.

Стало быть, пропорционально возрастает число поглощённых фотонов и, соответственно, число выбитых за секунду электронов.

2. Выразим из формулы (4) кинетическую энергию:

Действительно, кинетическая энергия выбитых электронов линейно растёт с частотой и не зависит от интенсивности света.

Зависимость кинетической энергии от частоты имеет вид уравнения прямой, проходящей через точку . Этим полностью объясняется ход графика на рис. 3 .

3. Для того, чтобы начался фотоэффект, энергии фотона должно хватить как минимум на совершение работы выхода: . Наименьшая частота , определяемая равенством

как раз и будет красной границей фотоэффекта. Как видим, красная граница фотоэффекта определяется только работой выхода, т.е. зависит лишь от вещества облучаемой поверхности катода.

Если , то фотоэффекта не будет — сколько бы фотонов за секунду не падало на катод. Следовательно, интенсивность света роли не играет; главное — хватает ли отдельному фотону энергии, чтобы выбить электрон.

Уравнение Эйнштейна (4) даёт возможность экспериментального нахождения постоянной Планка. Для этого надо предварительно определить частоту излучения и работу выхода материала катода, а также измерить кинетическую энергию фотоэлектронов.

В ходе таких опытов было получено значение , в точности совпадающее с (3) . Такое совпадение результатов двух независимых экспериментов — на основе спектров теплового излучения и уравнения Эйнштейна для фотоэффекта — означало, что обнаружены совершенно новые «правила игры», по которым происходит взаимодействие света и вещества. В этой области классическая физика в лице механики Ньютона и электродинамики Максвелла уступает место квантовой физике — теории микромира, построение которой продолжается и сегодня.

Видео:Глюоны: самые странные частицы в квантовой физикеСкачать

Гипотеза Планка о квантах. Фотоэффект. Фотон. Волновые и корпускулярные свойства света

Просмотр содержимого документа
«Гипотеза Планка о квантах. Фотоэффект. Фотон. Волновые и корпускулярные свойства света»

Строение атома и квантовая физика.

Гипотеза Планка о квантах. Фотоэффект. Фотон. Волновые и корпускулярные свойства света.

Электродинамика Максвелла приводила к бессмысленному выводу: нагретое тело в результате постоянного излучения электромагнитных волн должно было охладиться до нуля.

С точки зрения классической физики теплового равновесия между веществом и излучением существовать не может. На опыте доказано, что нагретое тело не тратит всю свою энергию на излучение электромагнитных волн.

В 1900 году Макс Планк выдвинул квантовую гипотезу.

Нагретое тело испускает и поглощает свет не непрерывно, а определенными конечными порциями энергии – квантами (квант (от лат. quantum) – количество).

Энергия каждой порции прямо пропорциональна частоте излучения.

Универсальная Планка (h) – постоянная универсальная величина.

Энергия квантов разного цвета имеет разное значение

Макс Планк выдвинул гипотезу о дискретной природе света. Эта явление было подтверждено исследованиями, которые проводил Генрих Герц. Такое явление получило название – явление фотоэффекта.

Изучил экспериментально и сформулировал законы фотоэффекта русский физик Александр Григорьевич Столетов

Фотоэффект – это вырывание электронов из вещества под действием света.

Внутренний фотоэффект – это эффект, при котором оторванные от своих атомов электроны остаются внутри вещества и становятся свободными. Такой фотоэффект можно наблюдать в полупроводниках и некоторых диэлектриках.

Для того чтобы получить о фотоэффекте более полное представление, нужно выяснить:

1. От чего зависит число вырванных светом с поверхности вещества электронов (фотоэлектронов),

2. Чем определяется их скорость или кинетическая энергия.

Были проведены экспериментальные исследования:

В стеклянный баллон, из которого был выкачан воздух, помещаются два электрода. На один из электродов поступает свет через кварцевое окошко, прозрачное не только для видимого света, но и для ультрафиолетового. На электроды подается напряжение, которое можно менять с помощью потенциометра и измерять вольтметром. К освещаемому электроду подключают отрицательный полюс батареи. Под действием света этот электрод испускает электроны, которые образуют электрический ток. При малых напряжениях не все вырванные светом электроны достигают другого электрода. Если, не меняя интенсивности излучения, увеличивать разность потенциалов между электродами, то сила тока возрастает. При некотором значении напряжения она достигает максимального значения, после чего перестает увеличиваться.

Ток насыщения (Iн) – максимальное значение силы тока. Ток насыщения определяется числом электронов, испущенных за 1 секунду освещаемым электродом.

Изменяя интенсивность излучения, удалось установить, что сила тока насыщения прямо пропорциональна интенсивности светового излучения, падающего на поверхность тела. При увеличении интенсивности излучения источника света в два раза, сила тока насыщения тоже увеличивается в два раза.

Если изменить полярность батареи, то сила тока будет уменьшаться, и при некотором напряжении обратной полярности она станет равна нулю.

Это значит, что электрическое поле тормозит вырванные электроны до полной остановки, а затем возвращает их на электрод. Такое напряжение – задерживающее напряжение

Измеряя задерживающее напряжение и применяя теорему о кинетической энергии, можно найти значение кинетической энергии фотоэлектронов:

При изменении интенсивности света задерживающее напряжение не меняется. Это значит, что не меняется кинетическая энергия фотоэлектронов.

Второй закон Столетова: максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и не зависит от его интенсивности

Красная граница фотоэффекта – это минимальная частота света для данного вещества, при которой наблюдается явление фотоэффекта.

С/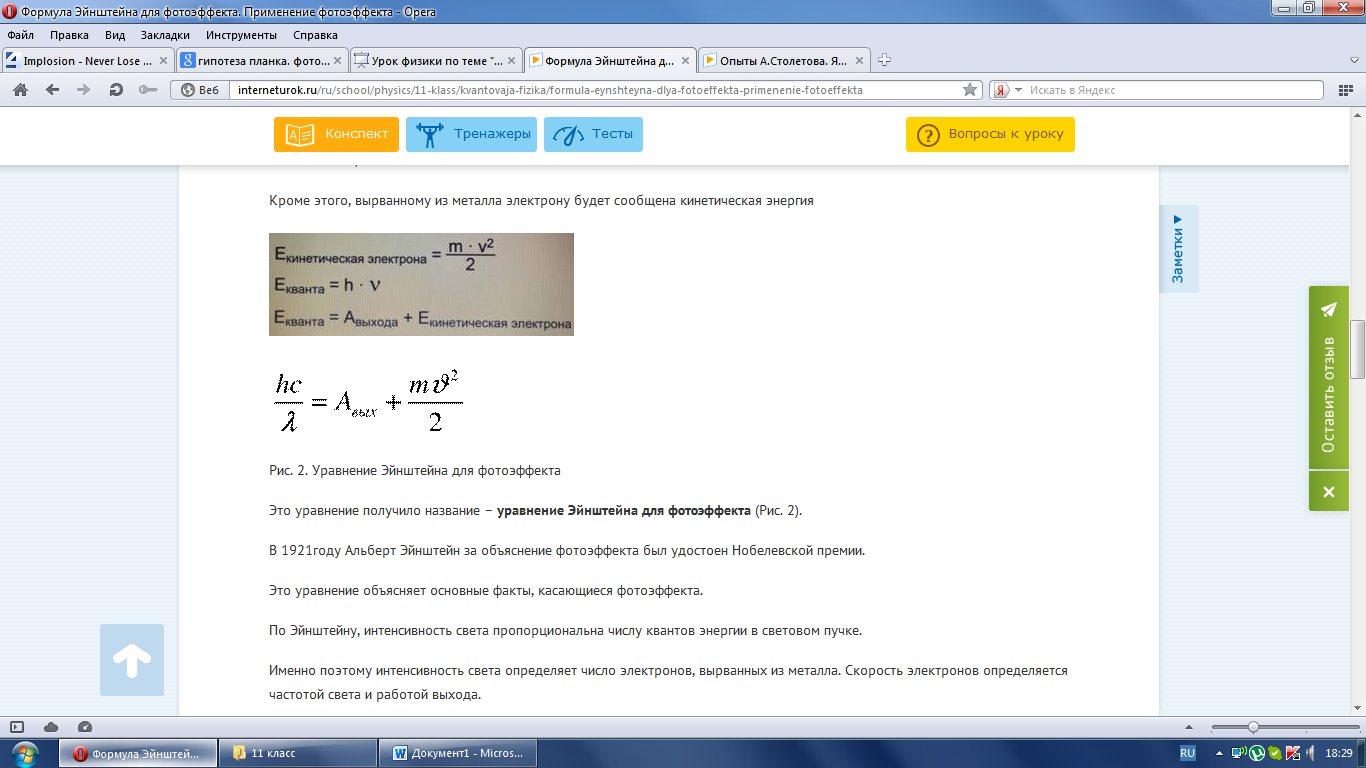=V(частота

Это уравнение получило название – уравнение Эйнштейна для фотоэффекта.

В 1921году Альберт Эйнштейн за объяснение фотоэффекта был удостоен Нобелевской премии.

С помощью фотоэффект появился звук в кинофильмах, и стала возможной передача движущихся изображений

Применение фотоэлектронных приборов позволило создать станки, которые без всякого участия человека изготовляют детали по заданным чертежам. Также созданы аппараты, которые изучают далекие небесные тела.

Основанные на фотоэффекте приборы контролируют размеры изделия лучше любого человека, вовремя включают и выключают маяки и уличное освящение.

Фотоэлемент – устройство, в котором энергия света управляет энергией электрического тока или преобразуется в нее

Волновые и корпускулярные свойства света.

В конце XVII века возникли две научные гипотезы о природе света — корпускулярная и волновая.

Согласно корпускулярной теории, свет представляет собой поток мельчайших световых частиц (корпускул), которые летят с огромной скоростью. Ньютон считал, что движение световых корпускул подчиняется законам механики. Так, отражение света понималось аналогично отражению упругого шарика от плоскости. Преломление света объяснялось изменением скорости частиц при переходе из одной среды в другую.

Волновая теория рассматривала свет как волновой процесс, подобный механическим волнам.

Согласно современным представлениям, свет имеет двоякую природу, т.е. он одновременно характеризуется и корпускулярными, и волновыми свойствами. В таких явлениях, как интерференция и дифракция, на первый план выступают волновые свойства света, а в явлении фотоэффекта, — корпускулярные.

Световой луч – это пучок света, толщина которого много меньше расстояния, на которое он распространяется. Такое определение близко, например, к определению материальной точки, которое дается в кинематике.

Определить энергию квантов, соответствующую длине волны 760 нм.

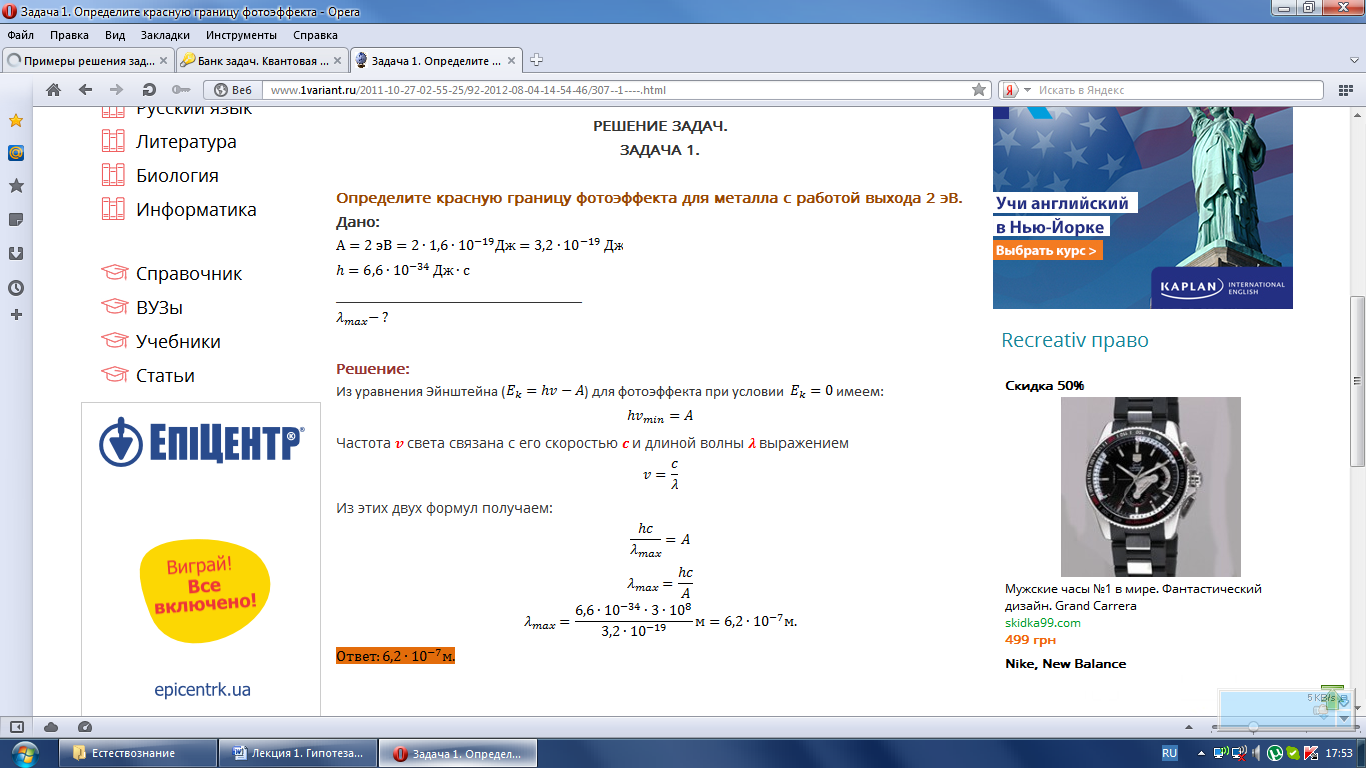
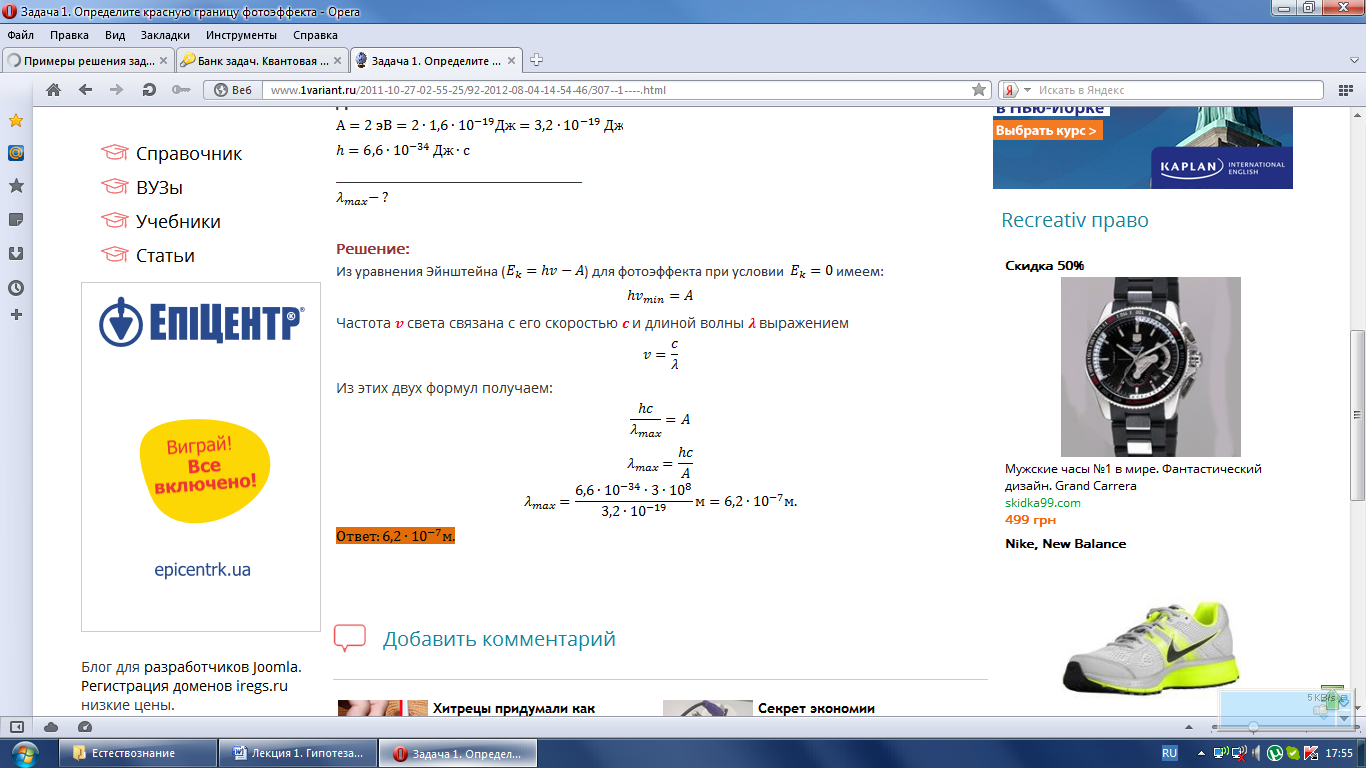
Определите красную границу фотоэффекта для металла с работой выхода 2 эВ.

Найдите максимальную скорость электронов, освобождаемых при фотоэффекте светом с длиной волны 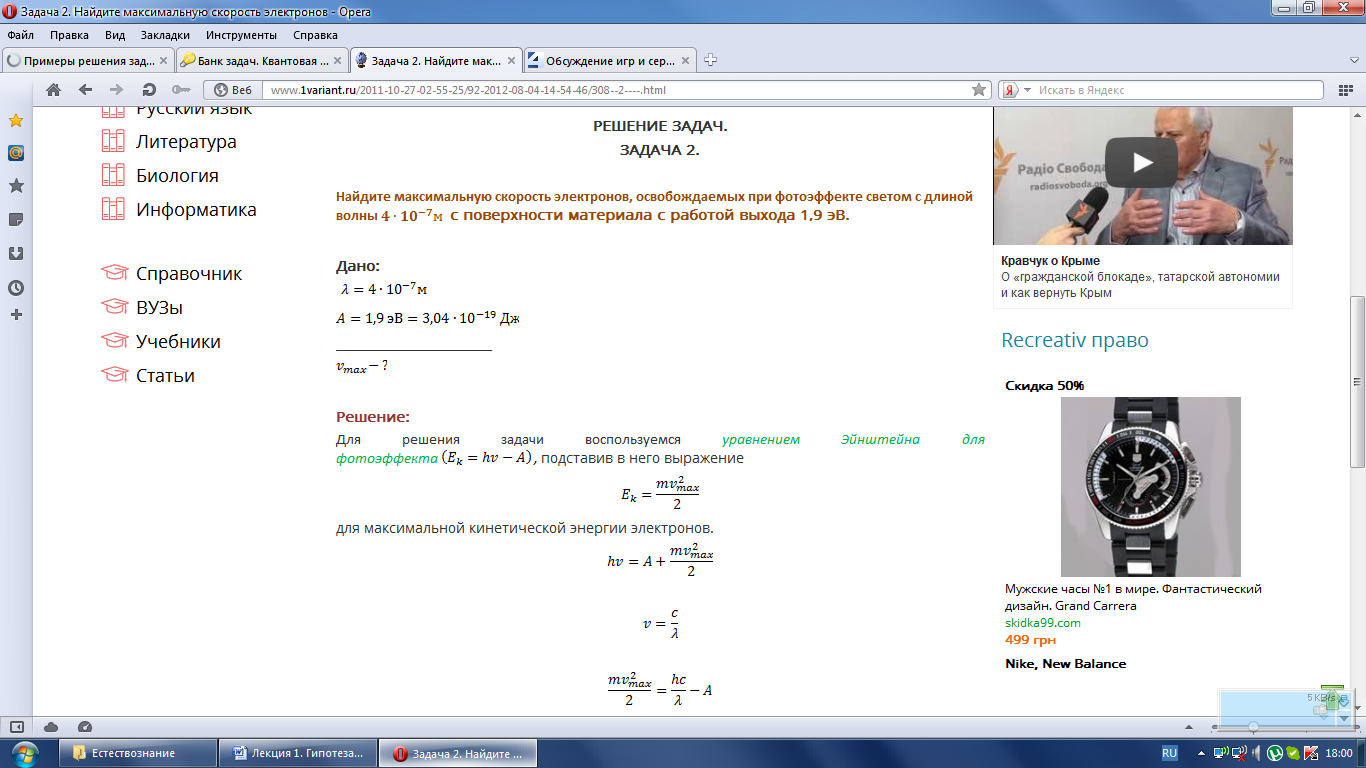с поверхности материала с работой выхода 1,9 эВ.

🎦 Видео

Эксперимент, который взрывает мозг!Скачать

Фотоэлектрический эффект. Опыты А. Столетова. Уравнение Эйнштейна для фотоэффектаСкачать

ФОТОЭФФЕКТ. Гипотеза Планка. Граница фотоэффекта. Подготовка к ЕГЭ по Физике | Николай НьютонСкачать

Задача: УРАВНЕНИЕ ЭЙНШТЕЙНА ДЛЯ ФОТОЭФФЕКТА.Скачать

Квантовая гипотеза Планка. Видеоурок по физике 11 классСкачать

ЧТО ВАЖНО ПОНИМАТЬ О КВАНТОВОМ УСТРОЙСТВЕ МИРА? | IQСкачать

ФОТОЭФФЕКТ в ЕГЭ по Физике 2021 // Николай НьютонСкачать

Опыты Столетова. ФотоэффектСкачать

Законы фотоэффектаСкачать

Физика. ЕГЭ. Фотоэффект теория. Уравнение Эйнштейна.Скачать