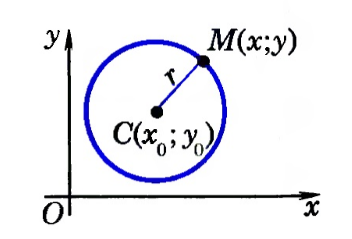Геометрия уравнение прямой и окружности (7 видео)

§ 3. Уравнения окружности и прямой

При изучении алгебры мы строили графики некоторых функций в прямоугольной системе координат, например график функции у-х. Известно, что графиком этой функции является прямая, проходящая через точки О (0; 0) и А(1;1) (рис. 284). Координаты любой точки М (х; у), лежащей на прямой О А, удовлетворяют уравнению у = х (так как ММ₁ = ММ₂), а координаты любой точки, не лежащей на прямой ОА, этому уравнению не удовлетворяют. Говорят, что уравнение у = х является уравнением прямой О А. Введём теперь понятие уравнения произвольной линии.

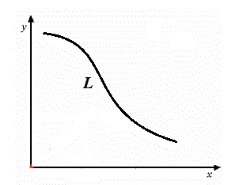
Пусть на плоскости задана прямоугольная система координат Оху и дана некоторая линия L (рис. 285). Уравнение с двумя переменными х и у называется уравнением линии L, если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

При изучении линий методом координат возникают две задачи: 1) по геометрическим свойствам данной линии найти её уравнение; 2) обратная задача: по заданному уравнению линии исследовать её геометрические свойства. В следующем пункте мы рассмотрим первую из этих задач применительно к окружности. Вторая задача рассматривалась в курсе алгебры при построении графиков функций.

Содержание

Уравнение окружности
Уравнение прямой
Взаимное расположение двух окружностей
Использование уравнений окружности и прямой при решении задач
Ответы к § 3
Геометрия. 9 класс
НАШИ ПАРТНЁРЫ
Уравнение окружности и прямой
Уравнение линии на плоскости
Уравнение окружности
Готовые работы на аналогичную тему
Пример задачи на нахождение уравнений линий в декартовой системе координат
💥 Видео

Уравнение окружности

Выведем уравнение окружности радиуса г с центром С в заданной прямоугольной системе координат. Пусть точка С имеет координаты (x₀; у₀) (рис. 286). Расстояние от произвольной точки М (х; у) до точки С вычисляется по формуле Если точка М лежит на данной окружности, то МС = r, МС 2 = r 2 , т. е. координаты точки М удовлетворяют уравнению

Если же точка М (х; у) не лежит на данной окружности, то МС 2 ≠ r 2 , и, значит, координаты точки М не удовлетворяют уравнению (1). Следовательно, в прямоугольной системе координат уравнение окружности радиуса r с центром в точке С (х₀; у₀) имеет вид:

(х — х₁) 2 + (у — у₀) 2 = r 2 .

В частности, уравнение окружности радиуса r с центром в начале координат имеет вид:

Найти уравнение окружности с центром в точке (-3; 4), проходящей через начало координат.

Центр окружности имеет координаты (-3; 4). Поэтому уравнение этой окружности можно записать в виде (х + 3) 2 + (у — 4) 2 = r 2 , где r — пока неизвестный радиус окружности. Найдём его. Для этого воспользуемся тем, что окружность проходит через начало координат, т. е. координаты точки О (0; 0) удовлетворяют этому уравнению: (0 + 3) 2 + (0 — 4) 2 = r 2 . Отсюда r 2 = 25, и, значит, r = 5. Итак, искомое уравнение окружности имеет вид (х + 3) 2 + (у — 4) 2 = 25.

Если раскрыть скобки и привести подобные члены, то получится уравнение х 2 + у 2 + 6х — 8у = 0, которое также является уравнением данной окружности.

Уравнение прямой

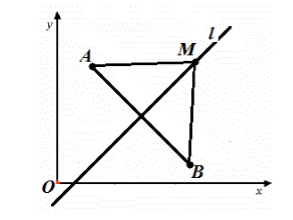
Выведем уравнение данной прямой l в заданной прямоугольной системе координат. Отметим две точки А (x₁; у₁) и В (х₂; у₂) так, чтобы прямая l была серединным перпендикуляром к отрезку АВ (рис. 287, а). Если точка М (х; у) лежит на прямой l, то АМ = ВМ, или AM 2 = ВМ 2 , т. е. координаты точки М удовлетворяют уравнению

Если же точка М (x; у) не лежит на прямой l, то AM 2 ≠ ВМ 2 , и, значит, координаты точки М не удовлетворяют уравнению (2). Следовательно, уравнение (2) является уравнением прямой I в заданной системе координат. После возведения выражений в скобках в квадрат и приведения подобных членов уравнение (2) принимает вид

где а = 2 (х₁ — х₂), b = 2(у₁ — у₂), Так как А (x₁; у₁) и В (x₂; y₂) — различные точки, то хотя бы одна из разностей (х₁ — х₂) и (у₁ — у₂) не равна нулю, т. е. хотя бы один из коэффициентов а и b отличен от нуля. Таким образом, уравнение прямой в прямоугольной системе координат является уравнением первой степени.

Если в уравнении (3) коэффициент b отличен от нуля, то это уравнение можно записать так:

где Число k называется угловым коэффициентом прямой, заданной этим уравнением. Докажите самостоятельно, что:

две параллельные прямые, не параллельные оси Оу, имеют одинаковые угловые коэффициенты; вели две прямые имеют одинаковые угловые коэффициенты, то эти прямые параллельны.

Выведем уравнение прямой l, проходящей через точку М₀ (x₀; у₀) и параллельной оси Оу (рис. 287, б). Абсцисса любой точки М (х; у) прямой l равна x₀, т. е. координаты любой точки М (x; у) прямой l удовлетворяют уравнению х = х₀. В то же время координаты любой точки, не лежащей на прямой l, этому уравнению не удовлетворяют. Следовательно, уравнение х = х₀ является уравнением прямой l.

Ясно, что ось Ох имеет уравнение у = О, а ось Оу — уравнение х = 0.

Взаимное расположение двух окружностей

Исследуем взаимное расположение двух окружностей в зависимости от их радиусов r, R и расстояния d между их центрами. Для определённости будем считать, что r ≤ R.

Если центры окружностей совпадают, т. е. d = 0, то окружности называются концентрическими, и окружность радиуса г лежит внутри круга радиуса R (рис. 288, а).

Пусть d > 0. Введём прямоугольную систему координат Оху так, чтобы точка О была центром первой окружности, а точка с координатами (d; 0) — центром второй окружности. В этой системе координат уравнения первой и второй окружностей имеют вид

х 2 + у 2 = R 2 , (х — d) 2 + у 2 = r 2 . (4)

Если система уравнений (4) имеет решением пару чисел х = х₀, у = у₀, то точка М0 (х₀; у₀) является общей точкой данных окружностей (рис. 288, б), и обратно: если М₀ (x₀; у₀) — общая точка данных окружностей, то пара чисел х = х₀, у = у₀ является решением системы уравнений (4).

Пусть система (4) имеет решением пару чисел x = х₀, у = у₀, т. е. справедливы числовые равенства

Вычитая из первого равенства второе, подучаем равенство 2x₀d — d 2 = R 2 — r 2 , откуда

Заметим, что х₀ > 0, поскольку R ≥ r и d > 0. Кроме того, как следует из первого равенства (5), х₀ = т. е. для величин R, r и d должно выполняться неравенство или R 2 + d 2 — r 2 ≤ 2dR. Последнее неравенство запишем в виде (d — R) 2 ≤ r 2 . Отсюда следует, что -r ≤ d — R ≤ r, или

Отметим, что х₀ = R, если d = R — r или d = R + r, и x₀ R + r (рис. 288, г). В этом случае говорят, что одна окружность лежит вне другой.

Если неравенства (7) выполнены, то возможны три случая:

3) d = R — r, при этом R > r, поскольку d > 0. Как уже было отмечено, в этом случае x₀ = R, поэтому из первого из равенств (5) следует, что y₀ = 0. Непосредственной проверкой можно убедиться в том, что пара чисел x = R, у = 0 есть решение системы (4). Таким образом, в данном случае окружности имеют ровно одну общую точку, и их взаимное расположение изображено на рисунке 288, д. Говорят, что окружности касаются изнутри.

4) d = R + r. В этом случае также х₀ = R, поэтому y₀ = 0, и непосредственно проверяется, что пара чисел x = R, у = 0 есть решение системы (4). Таким образом, в данном случае, как и в случае 3, окружности имеют ровно одну общую точку, но их взаимное расположение иное (рис. 288, е). Говорят, что окружности касаются извне.

5) R — r 2 + у 2 = 9; б) (х — 1) 2 + (у + 2) 2 = 4; в) (х + 5) 2 + (у — 3) 2 = 25; г) (х — 1) 2 + у 2 = 4; д) х 2 + (у + 2) 2 = 2.

960. Какие из точек А (3; -4), В (1; 0), С (0; 5), D (0; 0) и Е (0; 1) лежат на окружности, заданной уравнением:

а) х 2 + у 2 = 25; б) (х — 1) 2 + (у + 3) 2 = 9; в) (х — 0,5) 2 — у 2 = 0,25;

961. Окружность задана уравнением (х + 5) 2 + (у — 1) 2 = 16. Не пользуясь чертежом, укажите, какие из точек А (-2; 4), В (-5; -3), С (-7; -2) и D (1; 5) лежат:

а) внутри круга, ограниченного данной окружностью;
6) на окружности;
в) вне круга, ограниченного данной окружностью.

962. Даны окружность х 2 + у 2 = 25 и две точки А (3; 4) и В (4;-3). Докажите, что АВ — хорда данной окружности.

963. На окружности, заданной уравнением х 2 + у 2 = 25, найдите точки: а) с абсциссой -4; б) с ординатой 3.

964. На окружности, заданной уравнением (x — 3) 2 + (у — 5) 2 = 25, найдите точки: а) с абсциссой 3; б) с ординатой 5.

965. Напишите уравнения окружностей с центром в начале координат и радиусами r₁ = 3, r₂ = √2, r₂ = 5/2.

966. Напишите уравнение окружности радиуса r с центром А, если: а) А (0; 5), r = 3; б) А (-1;2), r = 2; в) А (-3;-7), r = 1/2; г) А (4;-3), r =10.

967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).

968. Напишите уравнение окружности с центром в точке А (0; 6), проходящей через точку В (-3; 2).

969. Напишите уравнение окружности с диаметром MN, если: а) М (-3; 5), N (7; -3); б) М (2; -1), N (4; 3).

970. Напишите уравнение окружности, проходящей через точку А (1;3), если известно, что центр окружности лежит на оси абсцисс, а радиус равен 5. Сколько существует таких окружностей?

971. Напишите уравнение окружности, проходящей через точки А (-3; 0) и В (0; 9), если известно, что центр окружности лежит на оси ординат.

972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2); б) С (2; 5) и D (5; 2); в) М (0; 1) и N (-4; -5).

а) Уравнение прямой АВ имеет вид ах + by + с = 0. Так как точки А и В лежат на прямой АВ, то их координаты удовлетворяют этому уравнению:

а • 1 + b • (-1) + с = 0, а • (-3) + b • 2 + с = 0,
или а — b + с = 0, -3а + 2b + с = 0.

Из этих уравнений выразим коэффициенты а и b через с: а = 3с, b = 4с. Подставив эти значения в уравнение прямой, получим 3сх + 4су + с = 0. При любом с ≠ 0 это уравнение является уравнением прямой АВ. Сократив на с, запишем искомое уравнение в виде 3х + 4у + 1 = 0.

973. Даны координаты вершин треугольника АВС: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнение прямой, содержащей медиану СМ.

974. Даны координаты вершин трапеции ABCD: А (-2; -2), В (-3;1), С (7; 7) и D (3; 1). Напишите уравнения прямых, содержащих: а) диагонали АС и BD трапеции; б) среднюю линию трапеции.

975. Найдите координаты точек пересечения прямой 3х — 4у + 12 = О с осями координат. Начертите эту прямую.

976. Найдите координаты точки пересечения прямых 4х + 3у — 6 = О и 2х + у — 4 = 0.

977. Напишите уравнения прямых, проходящих через точку М (2; 5) и параллельных осям координат.

978. Начертите прямую, заданную уравнением: а) у = 3; б) х = -2; в) у = -4; г) х = 7.

979. Найдите ординату точки М, лежащей на прямой АВ, если известно, что А (-8; -6), В (-3; -1) и абсцисса точки М равна 5.

980 Напишите уравнения прямых, содержащих стороны ромба, диагонали которого равны 10 см и 4 см, если известно, что его диагонали лежат на осях координат.

Использование уравнений окружности и прямой при решении задач

981. Даны две точки А и В. Найдите множество всех точек, для каждой из которых расстояние от точки А в два раза больше расстояния от точки В.

Введём прямоугольную систему координат так, как показано на рисунке 289,а. Тогда точки А и В имеют координаты А (0; 0), В (а; 0), где а = АВ.

Найдём расстояния от произвольной точки М (х; у) до точек А и В:

Если точка М (х; у) принадлежит искомому множеству, то

AM = 2ВМ, или AM 2 = 4ВМ 2 .

Поэтому её координаты удовлетворяют уравнению

х 2 + у 2 = 4 ((х — а) 2 + у 2 ). (8)

Если же точка М не принадлежит искомому множеству, то её координаты не удовлетворяют этому уравнению.

Следовательно, уравнение (8) и есть уравнение искомого множества точек в выбранной системе координат. Раскрывая скобки и группируя слагаемые соответствующим образом, приводим уравнение (8) к виду

Таким образом, искомым множеством точек является окружность радиуса 2/3a с центром в точке C(4/3a; 0). Эта окружность изображена на рисунке 289, б.

Аналогично можно доказать, что множеством всех точек М, удовлетворяющих условию AM = kBM, где k — данное положительное число, не равное единице, является окружность радиуса с центром в точке

Эти окружности, соответствующие различным значениям k ≠ 1, называют окружностями Аполлония, поскольку они рассматривались ещё древнегреческим математиком Аполлонием в его трактате «О кругах» во II в. до н. э.

Если k = 1, то задача сводится к известной нам задаче о нахождении множества всех точек, равноудалённых от точек А и В. Таким множеством, как мы знаем, является серединный перпендикуляр к отрезку АВ.

982. Точка В — середина отрезка АС, длина которого равна 2. Найдите множество всех точек М, для каждой из которых: a) AM 2 + ВМ 2 + СМ 2 = 50; б) AM 2 + 2ВМ 2 + 3СМ 2 = 4.

983. Даны две точки А и В. Найдите множество всех точек М, для каждой из которых AM 2 + ВМ 2 = k 2 , где k — данное число.

984. Даны две точки А и В. Найдите множество всех точек М, для каждой из которых AM 2 — ВМ 2 = k, где k — данное число.

Введём прямоугольную систему координат так, чтобы точка А была началом координат, а точка В имела координаты (а; 0), где а = АВ. Найдём расстояния от произвольной точки М (х; у) до точек А и В:

Если точка М (х; у) принадлежит искомому множеству, то AM 2 — ВМ 2 = k, поэтому координаты точки М удовлетворяют уравнению х 2 + у 2 — (х — а) 2 — у 2 = k, или 2ах — а 2 — k = 0.

Если же точка М не принадлежит искомому множеству, то её координаты не удовлетворяют этому уравнению. Итак, полученное уравнение является уравнением искомого множества точек. Но этим уравнением определяется прямая, параллельная оси Оу, если а 2 + k ≠ 0, и сама ось Оу, если a 2 + k = 0. Таким образом, искомым множеством точек является прямая, перпендикулярная к прямой АВ.

985. Даны две точки А и B. Найдите множество всех точек М, для каждой из которых ВМ 2 — AM 2 = 2АВ 2 .

986. Дан прямоугольник ABCD. Найдите множество всех точек М, для каждой из которых

(AM 2 + DM 2 ) — (ВМ 2 + СМ 2 ) = 2АВ 2 .

987.* Дан ромб ABCD, диагонали которого равны 2а и 2Ь. Найдите множество всех точек М, для каждой из которых

AM 2 + DM 2 = ВМ 2 + СМ 2 .

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Ответы к § 3

960. а) А и С; б) В; в) В и D.

961. а) С; б) В; в) А и D.

963. а) (-4; -3), М;3);б) (4; 3), (-4; 3).

964. а) (3; 0), (3; 10); б) (-2; 5), (8; 5).

965. 1) х 2 + у 2 = 9; 2) х 2 + у 2 = 2; 3)

966. а) х 2 + (у-5) 2 = 9; б) (х + 1) 2 + (y — 2) 2 = 4; в) г) (х — 4) 2 + (y + 3) 2 = 100.

967. х 2 + у 2 = 10.

968. х 2 + (у — 6) 2 = 25.

969. а) (х — 2) 2 + (y — 1) 2 = 41; б) (х — 3) 2 + (у — 1) 2 = 5.

970. (х — 5) 2 + у 2 = 25, (х + 3) 2 + у 2 = 25; две окружности.

971. х 2 + (у — 4) 2 = 25.

972. б) х + у- 7 = 0; в) 3х — 2у + 2 = 0.

973. 7х — у + 3 = 0.

974. а) х — у = 0, у — 1 = 0; б) 3х — 5у + 5 = 0.

977. х = 2 и у = 5.

980. 5х + 2у — 10 = 0, 5х — 2у — 10 = 0, 5х + 2у + 10 = 0, 5х — 2у + 10 = 0 или 2х + 5у- 10 = 0, 2х — 5у -10 = 0, 2х + 5y + 10 = 0, 2х — 5у+ 10 = 0.

982. а) Окружность радиуса 4 с центром В; б) окружность радиуса 1/3 с центром D, лежащим на отрезке ВС, причём BD = 1/3

983. Окружность с центром в точке О радиуса , если k 2 > 2а 2 , и точка О, если k 2 = 2а 2 , где О — середина отрезка АВ и Если k 2 2 , то точек, удовлетворяющих условию задачи, не существует.

985. Серединный перпендикуляр к отрезку АВ’, где В’ и В — точки, симметричные относительно точки А.

986. Прямая ВС. Указание. Выбрать прямоугольную систему координат так, чтобы точки А и В лежали на оси Ох и были симметричны относительно оси Оу.

987. Прямая, проходящая через точку пересечения диагоналей ромба и перпендикулярная к стороне ромба.

Видео:УРАВНЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ 9 класс геометрияСкачать

Геометрия. 9 класс

Конспект
Введём уравнение произвольной линии.
В прямоугольной системе координат рассмотрим произвольную линию L.

Уравнение с двумя переменными х и у называется уравнением линии L, если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии.
Рассмотрим точки М и N в координатной плоскости.
y = f (x) – уравнение линии L, если выполняются условия:
М (х₁; у₁) ∈ L → y₁ = f (x₁)
N (х₂; у₂) ∉ L → y₂ ≠ f (x₂)
Теперь, зная метод координат и геометрические свойства окружности, выведем её уравнение.
Пусть в прямоугольной системе координат дана окружность, где C – центр окружности с координатами x₀ и y₀, а r – её радиус.
Расстояние от произвольной точки М с координатами х и у до точки С вычисляется по формуле:
Точка М лежит на окружности, то есть координаты точки М удовлетворяют этому уравнению. Значит, МС = r, MC₂ = r₂.
В прямоугольной системе координат уравнение окружности радиуса r и с центром (x — x₀) 2 + (y — y₀) 2 = r 2 имеет вид:
Если центр окружности находится в начале координат, то уравнение окружности с центром в начале координат будет выглядеть так:
Теперь выведем уравнение прямой. Снова рассмотрим прямоугольную систему координат.
Докажем, что любая прямая в декартовых координатах имеет уравнение ax + by + c = 0, где а, b, с – некоторые числа, а х и у – переменные координаты точки А, принадлежащей прямой.
Как и при составлении уравнения окружности, обратимся к свойству прямой, равноудаленной от двух данных точек. Пусть h – произвольная прямая на плоскости и точка А с координатами х и у – точка этой прямой. Точки В и С равноудалены от прямой h, точка D – это точка пересечения ВС с прямой h. Поэтому h – срединный перпендикуляр к отрезку ВС. Так как АС = АВ, то AС₂ = АB₂, значит координаты точки А удовлетворяют уравнению (х – хв)² + (у – ув)² = (х – хс)² + (у – ус)², где В (хв; ув) и С (хс; ус)
Следовательно, это уравнение и является уравнением прямой h в прямоугольной системе координат.
После алгебраических преобразований получаем уравнение прямой: ах + bу + с = 0, где a, b, c некоторые числа. Так как В и С различные точки, значит разность их координат не равна нулю.
Таким образом, уравнение прямой в прямоугольной системе координат является уравнением первой степени.

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

НАШИ ПАРТНЁРЫ

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Уравнение окружности и прямой

Вы будете перенаправлены на Автор24

Видео:Уравнение прямой. Урок 6. Геометрия 9 классСкачать

Уравнение линии на плоскости

Введем для начала понятие уравнения линии в двумерной системе координат. Пусть в декартовой системе координат построена произвольная линия $L$ (Рис. 1).

Рисунок 1. Произвольная линия в системе координат

Уравнение с двумя переменными $x$ и $y$ называется уравнением линии $L$, если этому уравнению удовлетворяют координаты любой точки, принадлежащей линии $L$ и не удовлетворяет ни одна точка, не принадлежащая линии $L.$

Видео:Уравнение окружности | Геометрия 7-9 класс #90| ИнфоурокСкачать

Уравнение окружности

Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ — произвольная точка этой окружности (рис. 2).

Рисунок 2. Окружность в декартовой системе координат

Расстояние от центра окружности до точки $M$ вычисляется следующим образом

Но, так как $M$ лежит на окружности, то получаем $CM=r$. Тогда получим следующее

Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.

В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид

Выведем уравнение прямой $l$ в декартовой системе координат $xOy$. Пусть точки $A$ и $B$ имеют координаты $left$ и $$ соответственно, причем точки $A$ и $B$ выбраны так, что прямая $l$ — серединный перпендикуляр к отрезку $AB$. Выберем произвольную точку $M=$, принадлежащую прямой $l$ (рис. 3).

Готовые работы на аналогичную тему

Рисунок 3. Прямая в декартовой системе координат

Так как прямая $l$ — серединный перпендикуляр к отрезку $AB$, то точка $M$ равноудалена от концов этого отрезка, то есть $AM=BM$.

Найдем длины данных сторон по формуле расстояния между точками:

Обозначим через $a=2left(x_1-x_2right), b=2left(y_1-y_2right), c=^2+^2-^2-^2$, Получаем, что уравнение прямой в декартовой системе координат имеет следующий вид:

Здесь можно выделить два частных случая для уравнения прямой. Пусть прямая $l$ проходит через точку $M=$, тогда

Если прямая $l$ параллельна оси $Ox$, то она имеет вид

Если прямая $l$ параллельна оси $Oy$, то она имеет вид

Видео:Уравнение окружности (1)Скачать

Пример задачи на нахождение уравнений линий в декартовой системе координат

Найти уравнение окружности с центром в точке $(2, 4)$. Проходящей через начало координат и прямую, параллельную оси $Ox,$ проходящей через её центр.

Решение.

Найдем сначала уравнение данной окружности. Для этого будем использовать общее уравнение окружности (выведенное выше). Так как центр окружности лежит в точке $(2, 4)$, получим

Найдем радиус окружности как расстояние от точки $(2, 4)$ до точки $(0,0)$

Получаем, уравнение окружности имеет вид:

Найдем теперь уравнение окружности, используя частный случай 1. Получим

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 05 04 2021