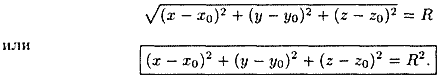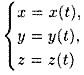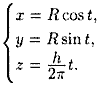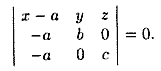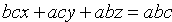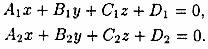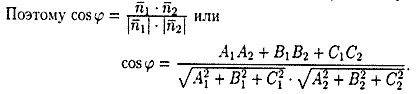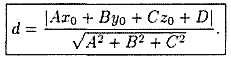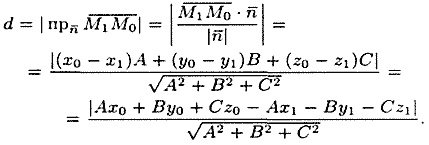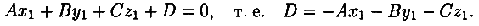В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.
Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Определение уравнения плоскости
Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.
Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х , у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.
Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.
Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Общее уравнение плоскости
Сформулируем теорему, а затем запишем уравнение плоскости.
Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А , В , С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве
Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А , В , С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.
Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.
Общим уравнениям плоскости x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.
Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .
Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А , B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.
Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.
Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y — 5 · z + 1 = 0 .
Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x — y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.
Важное уточнение: коэффициенты А , В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.
Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.
Видео:Уравнение плоскости. 11 класс.Скачать

Нормальное уравнение плоскости
Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = ( A , B , C ) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .
Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z — p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ — это направляющие косинусы нормального вектора данной плоскости единичной длины.
n → = ( cos α , cos β , cos γ ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1
То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = ( cos α , cos β , cos γ ) . Если p равно нулю, то плоскость проходит через начало координат.
Плоскость задана общим уравнением плоскости вида — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 . D = — 7 ≤ 0 , нормальный вектор этой плоскости n → = — 1 4 , — 3 4 , 6 4 имеет длину, равную единице, так как n → = — 1 4 2 + — 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.
Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.
Видео:2. Уравнение плоскости примеры решения задач #1Скачать

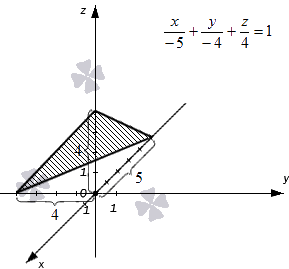
Уравнение плоскости в отрезках
Плоскость отсекает на координатных осях O х , O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с . Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а , b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.
Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .
Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.
Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x — 5 + y — 4 + z 4 = 1 .
Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.
Видео:Лекция 25. Виды уравнений плоскости в пространстве.Скачать

Геометрические места точек
Геометрическим местом точек называют множество точек, заданное условием, являющимся и свойством, и признаком.
Другими словами, все точки из рассматриваемого геометрического места точек, и только они, удовлетворяют заданному условию.
Примеры геометрических мест точек (сокращённо ГМТ ) на плоскости представлены в следующей таблице, причём геометрические места точек изображаются в таблице красным цветом .
Видео:Видеоурок "Общее уравнение плоскости"Скачать

Лекция № 10
Ссылки
Глава IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
§12. УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ
12.1. Основные понятия
Поверхность и ее уравнение
Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О1 есть геометрическое место всех точек пространства, находящихся от точки O1 на расстоянии R.
Прямоугольная система координат Oxyz в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и тройками чисел х, у и z — их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего координаты всех точек поверхности.
Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение F(x, у, z) = 0 с тремя переменными х, у и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х, у и z в уравнении поверхности называются текущими координатами точек поверхности.
Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения. Так, для того, чтобы узнать, лежит ли точка M1(x1;y1;z1) на данной поверхности, достаточно подстав и ть координаты точки M1 в уравнение поверхности вместо переменных: если эти координаты удовлетворяют уравнению, то точка лежит на поверхности, если не удовлетворяют — не лежит.
Найдем уравнение сферы радиуса R с центром в точке O1(x0;y0;z0). Согласно определению сферы расстояние любой ее точки М(х; у; z) от центра O1(x0;y0;z0) равно радиусу R, т. е. O1M= R. Но 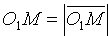
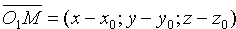
Это и есть искомое уравнение сферы. Ему удовлетворяют координаты любой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.
Если центр сферы Ο1 совпадает с началом координат, то уравнение сферы принимает вид 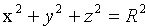
Если же дано уравнение вида F(x;y;z) = 0 , то оно, вообще говоря, определяет в пространстве некоторую поверхность.
Выражение «вообще говоря» означает, что в отдельных случаях уравнение F(x; y; z)=0 может определять не поверхность, а точку, линию или вовсе не определять никакой геометрический образ. Говорят, «поверхность вырождается».
Так, уравнению 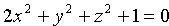
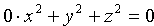
Итак, поверхность в пространстве можно задать геометрически и аналитически. Отсюда вытекает постановка двух основных задач:
1. Дана поверхность как геометрическое место точек. Найти уравнение этой поверхности.
2. Дано уравнение F(x;y;z) = 0. Исследовать форму поверхности, определяемой этим уравнением.
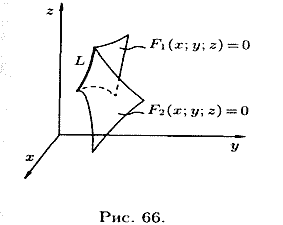
Уравнения линии в пространстве
Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (см. рис. 66) или как геометрическое место точек, общих двум поверхностям.
Если 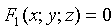
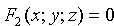
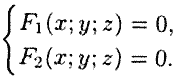
Сравнения системы (12.1) называются уравнениями линии в пространстве. Например, 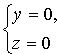
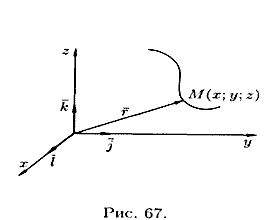
Линию в пространстве можно рассматривать как траекторию движения точки (см. рис. 67). В этом случае ее задают векторным уравнением
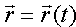

или параметрическими уравнениями
проекций вектора (12.2) на оси координат.
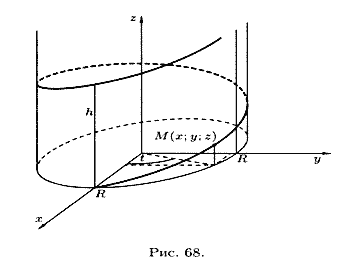
Например, параметрические уравнения винтовой линии имеют вид
Если точка Μ равномерно движется по образующей кругового цилиндра, а сам цилиндр равномерно вращается вокруг оси, то точка Μ описывает винтовую линию (см. рис. 68).
12.2. Уравнения плоскости в пространстве
Простейшей поверхностью является плоскость. Плоскость в пространстве Oxyz можно задать разными способами. Каждому из них соответствует определенный вид ее уравнения.
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
Пусть в пространстве Oxyz плоскость Q задана точкой 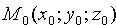
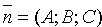
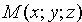
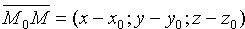
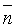
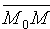
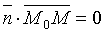
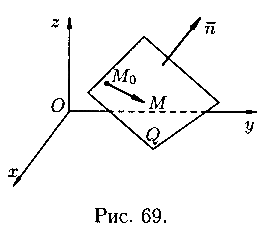

Координаты любой точки плоскости Q удовлетворяют уравнению (12.3), координаты точек, не лежащих на плоскости Q, этому уравнению не удовлетворяют (для них 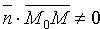
Уравнение (12.3) называется уравнением плоскости, проходящей через данную точку 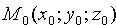
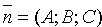
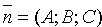
Придавая коэффициентам А, В и С уравнения (12.3) различные значения, можно получить уравнение любой плоскости, проходящей череp точку 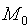
Общее уравнение плоскости
Рассмотрим общее уравнение первой степени с тремя переменными х, у и z:
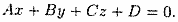
Полагая, что по крайней мере один из коэффициентов А, В или С не равен нулю, например 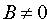
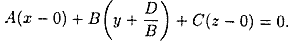
Сравнивая уравнение (12.5) с уравнением (12.3), видим, что уравнения (12.4) и (12.5) являются уравнением плоскости с нормальным вектором 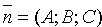
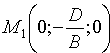
Итак, уравнение (12.4) определяет в системе координат Oxyz некоторую плоскость. Уравнение (12.4) называется общим уравнением плоскости.
Частные случаи общего уравнения плоскости:
1. Если D = 0, то оно принимает вид 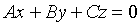
2. Если С = 0, то имеем уравнение 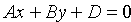
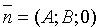
3. Если С = D = 0, то плоскость проходит через 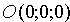
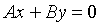
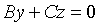
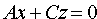
4. Если А = В = 0, то уравнение (12.4) принимает вид 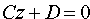
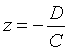
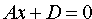
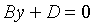
5. Если A = B = D = 0, то уравнение (12.4) примет вид 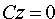
Уравнение плоскости, проходящей через три данные точки
Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдем уравнение плоскости Q, проходящей через три данные точки M1(x1;y1;z1), М2(x2;y2;z2) и М3(х3,y3,z3), не лежащие на одной прямой.
Возьмем на плоскости произвольную точку M(x;y;z) и составим векторы 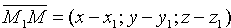
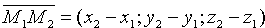
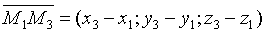
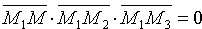

Уравнение (12.6) есть уравнение плоскости, проходящей через три данные точки.
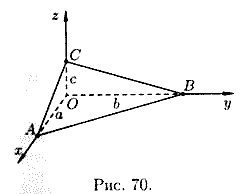
Уравнение плоскости в отрезках
Пусть плоскость отсекает на осях Ох, Оу и Оz соответственно отрезки a, b и c, т. е. проходит через три точки A(a;0;0), B(0;b;0) и C(0;0;c) (см.рис. 70). Подставляя координаты этих точек в уравнение (12.6), получаем
Раскрыв определитель, имеем 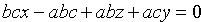

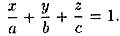
Уравнение (12.7) называется уравнением плоскости в отрезках на осях. Им удобно пользоваться при построении плоскости.
Нормальное уравнение плоскости
Положение плоскости Q вполне определяется заданием единичного вектора 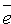
плоскость из начала координат, и длиной p этого перпендикуляра (см. рис. 71).
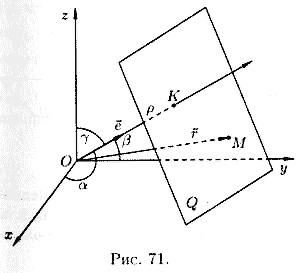
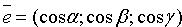
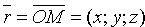
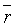
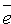
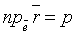
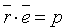
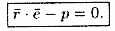
Уравнение (12.8) называется нормальным уравнением плоскости в векторной форме. Зная координаты векторов f и e , уравнение (12.8) перепишем в виде
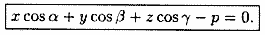
Уравнение (12.9) называется нормальным уравнением плоскости в координатной форме.
Отметим, что общее уравнение плоскости (12.4) можно привести к нормальному уравнению (12.9) так, как это делалось для уравнения прямой на плоскости. А именно: умножить обе части уравнения (12.4) на нормирующий множитель 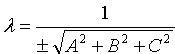
12.3. Плоскость. Основные задачи
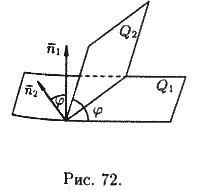
Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей
Пусть заданы две плоскости Q1 и Q2:
Под углом между плоскостями Q1 и Q2 понимается один из двугранных углов, образованных этими плоскостями.
Угол j между нормальными векторами 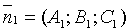
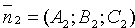
Для нахождения острого угла следует взять модуль правой части.
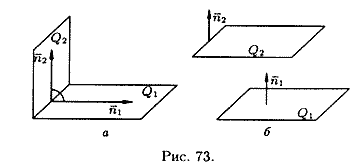
Если плоскости Q1 и Q2 перпендикулярны (см. рис. 73, а), то таковы же их нормали, т. е. 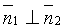
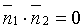
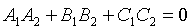
Если плоскости Q1 и Q2 параллельны (см. рис. 73, б), то будут параллельны и их нормали 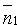
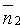
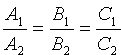
Расстояние от точки до плоскости
Пусть задана точка 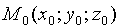
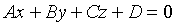
Вывод этой формулы такой же, как вывод формулы расстояния от точки 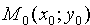
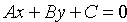
Расстояние d от точки M0 до плоскости Q равно модулю проекции вектора 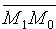
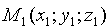
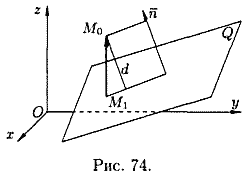
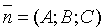
А так как точка 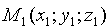
Поэтому 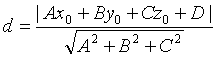
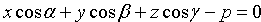
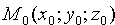
🌟 Видео
ГМТ // ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕКСкачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Уравнение плоскости через 3 точкиСкачать

Видеоурок "Уравнение плоскости по трем точкам"Скачать

5. Нормальное уравнение плоскости выводСкачать

11 класс, 8 урок, Уравнение плоскостиСкачать

Уравнение плоскости. Практика. Урок 5. Геометрия 11 классСкачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Частные случаи уравнения плоскости. 1 часть. 11 класс.Скачать

3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

11. Прямая в пространстве и ее уравненияСкачать

Векторный метод в стереометрии. Задача 14 профильный ЕГЭСкачать