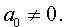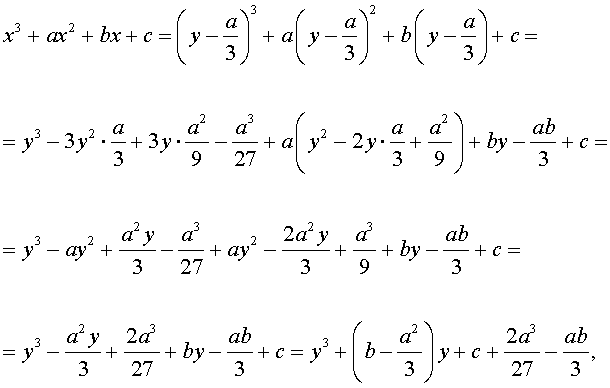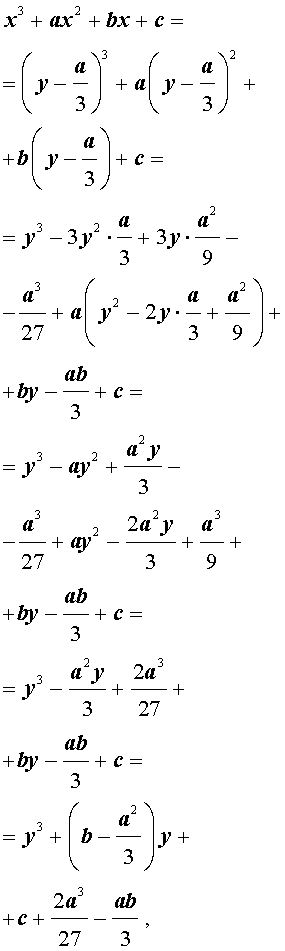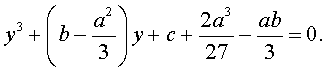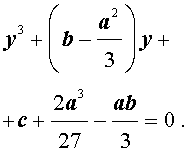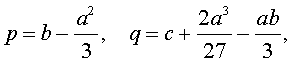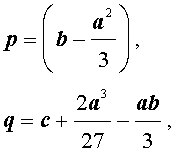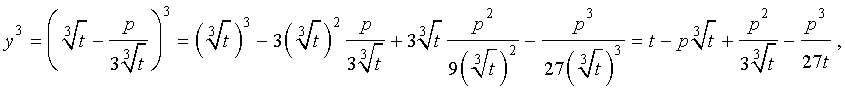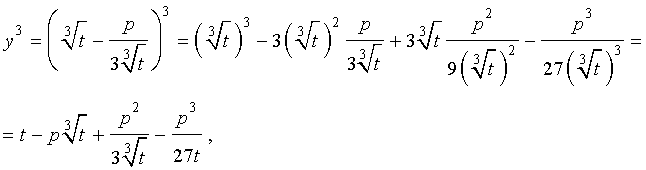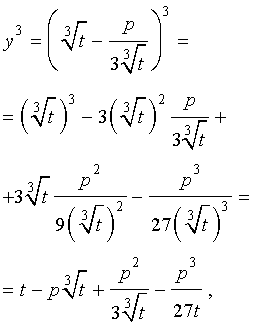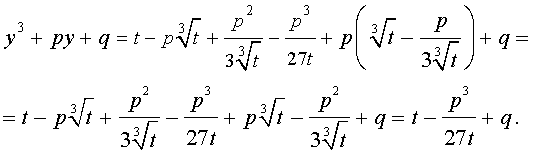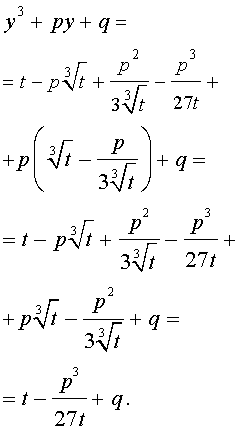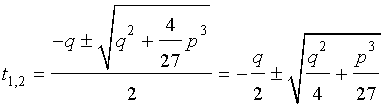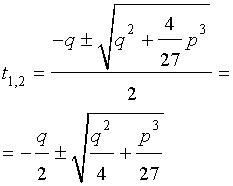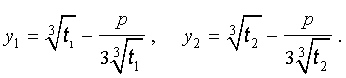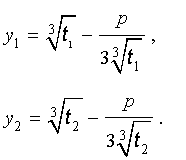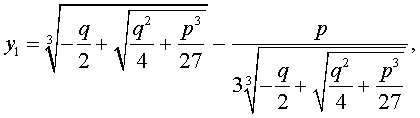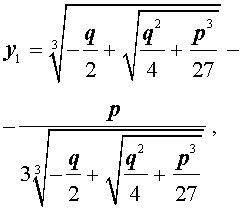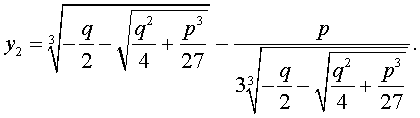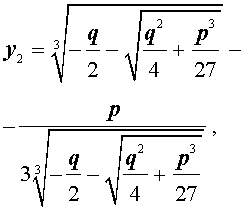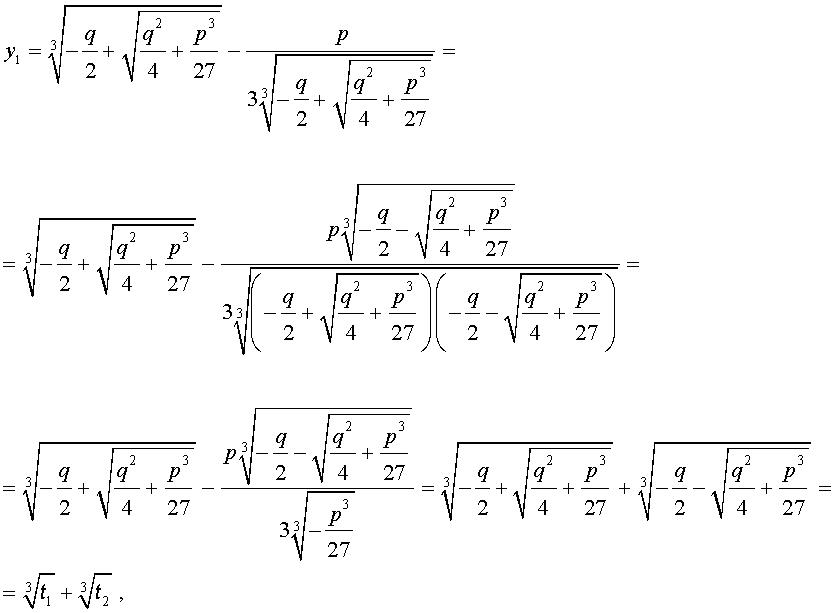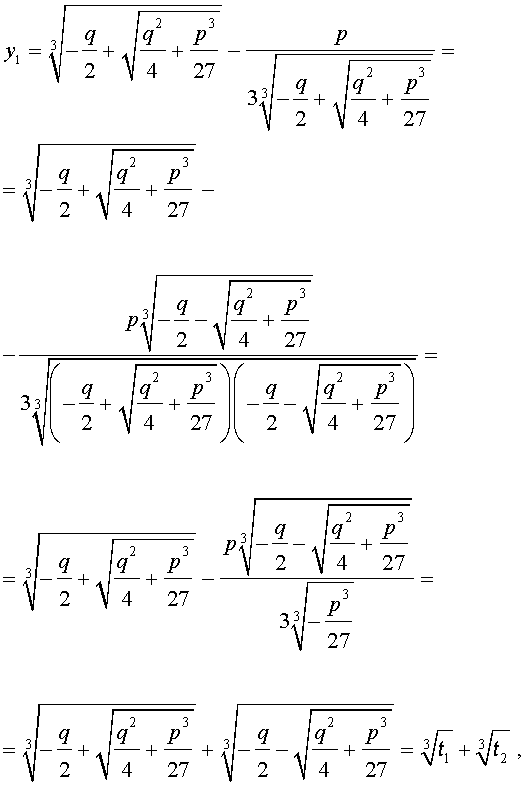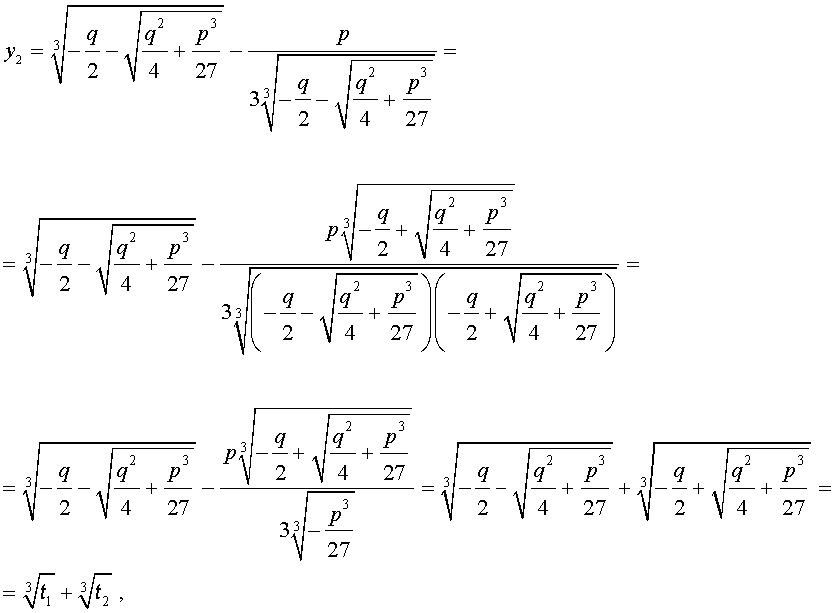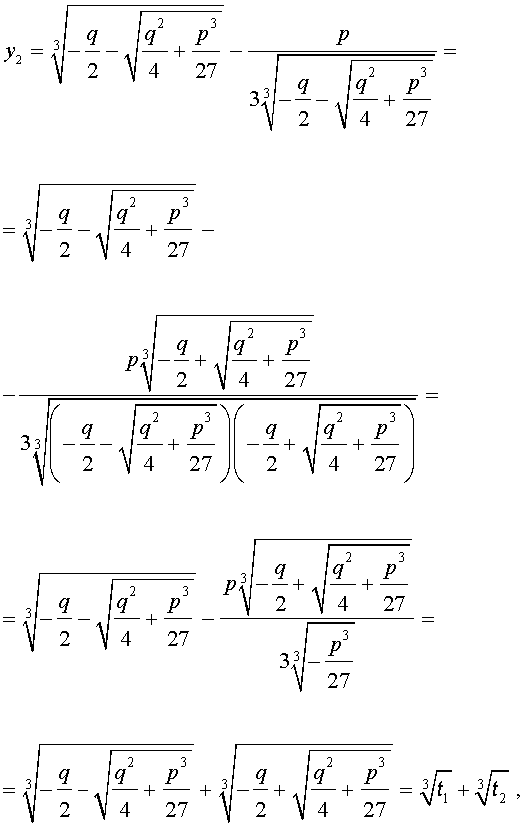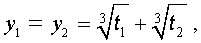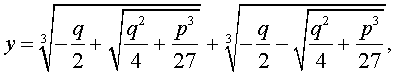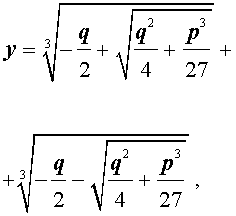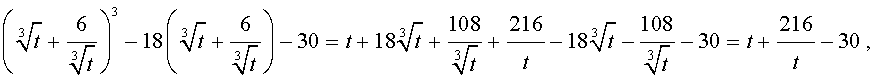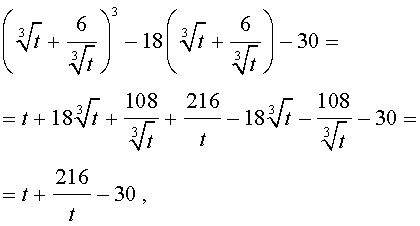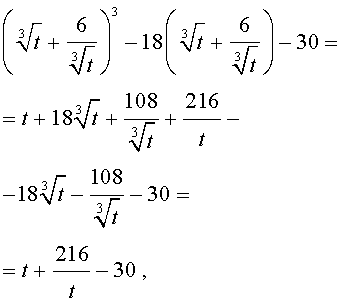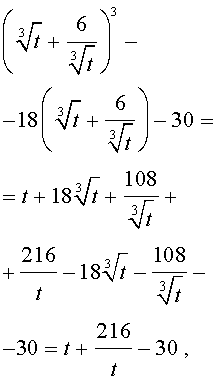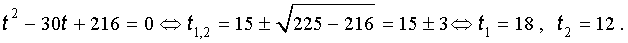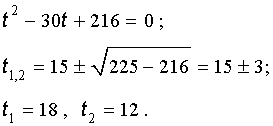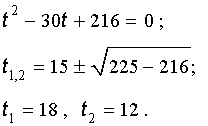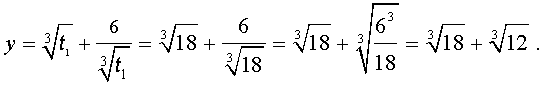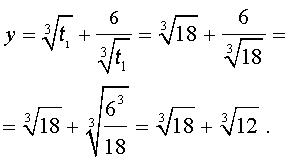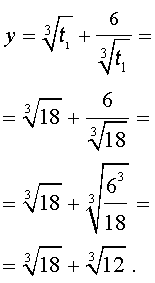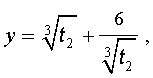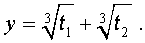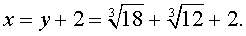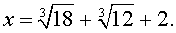Мы уже говорили, что уже арабские математики средневековья владели всей теорией решения квадратных уравнений. Другое дело – уравнения кубические. Если решение квадратных уравнений может быть найдено с помощью определенных построений циркулем и линейкой (эти построения, так называемые «приложения площадей», были известны уже древним грекам), то корень кубического уравнения, вообще говоря, невозможно построить циркулем и линейкой. Поэтому для их решений были нужны другие методы. Во-первых, существовали приближенные методы вычисления корней, с помощью которых можно было найти корень с любой заданной точностью. А во-вторых, для анализа разрешимости уравнения, числа его корней и примерной их оценки применялись графические методы.
Под графическим решением уравнения мы сейчас обычно понимаем (в простейшем случае) построение графиков функций и и нахождение абсцисс точек их пересечения. В более общем случае уравнение может быть сведено к системе каких-либо двух уравнений с двумя неизвестными – не обязательно эти уравнения должны иметь форму и . Каждое из уравнений трактуется как уравнение некоторой кривой на координатной плоскости; координаты точек их пересечения этих кривых удовлетворяют обоим уравнениям, и, следовательно, являются решением системы, по ним можно получить и корень исходного уравнения. Разумеется, с помощью графического решения, как правило, невозможно найти значение корней уравнения точно. Тем не менее, оно часто бывает полезным для того, чтобы приблизительно определить их значение или получить общее представление о числе положительных и отрицательных корней и т. п.
Хотя у древних греков не было идеи графиков функций в современном смысле, они владели определенной техникой, которую мы бы, в переводе на современный язык, сочли именно графическим решением уравнений. Задача, которую было необходимо решить, формулировалась в виде некоторого соотношения (уравнения), которое затем переводилось в форму двух соотношений между двумя неизвестными величинами (система двух уравнений с двумя неизвестными). Эти две величины трактовались как расстояния от точки до двух перпендикулярных прямых (фактически, осей координат): строились две кривые, соответствующие двум данным соотношениям между этими расстояниями (координатами), и находились точки пересечения этих кривых.
С помощью этой техники греки, а затем и арабы, находили, в частности, решения кубических уравнений. Уже говорилось, что с помощью точек пересечения гиперболы и параболы или двух парабол Менехм строил решение знаменитой задачи об удвоении куба, то есть решал уравнение вида 3 = . Греки сталкивались и с другими типами кубических уравнений. Так, Архимед рассматривал задачу о делении шара плоскостью на два сегмента, объемы которых находятся в данном отношении (1 : 2 = ). Эта задача сводится к решению кубического уравнения вида 3 + = 2 . Дело в том, что объем шарового сегмента (как это открыл тот же Архимед) является кубической функцией его высоты (да еще без линейного члена):
| = π 2 ( – / 3). |
Это довольно приятное обстоятельство: скажем, площадь кругового сектора зависит от его высоты существенно более сложным образом.
 | |||||||||||||||||||||||||||||||||||||||||||
| 4 3 – 3 2 + 3 = (3 2 – 3 ) , |
3 ( + 1) + 4 3 = 3 ( + 1) 2 ,
3 + 4 3 / ( + 1) = 3 2 .
Другой вариант – положить обратное отношение равным . Тогда:
- Решение кубических уравнений. Формула Кардано
- Схема метода Кардано
- Приведение кубических уравнений к трехчленному виду
- Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи
- Формула Кардано
- Пример решения кубического уравнения
- Решение кубических уравнений
- Решение двучленного кубического уравнения вида A x 3 + B = 0
- Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0
- Решение кубических уравнений с рациональными корнями
- Решение кубических уравнений по формуле Кардано
- 📺 Видео
Видео:Математика | Кубические уравнения по методу СталлонеСкачать

Решение кубических уравнений. Формула Кардано
 Схема метода Кардано Схема метода Кардано |
 Приведение кубических уравнений к трехчленному виду Приведение кубических уравнений к трехчленному виду |
 Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи |
 Формула Кардано Формула Кардано |
 Пример решения кубического уравнения Пример решения кубического уравнения |
Видео:ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать

Схема метода Кардано
Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени ( кубических уравнений )
| a0x 3 + a1x 2 + + a2x + a3= 0, | (1) |
где a0, a1, a2, a3 – произвольные вещественные числа,
Вывод формулы Кардано состоит из двух этапов.
На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями .
На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.
Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Приведение кубических уравнений к трехчленному виду
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x 3 + ax 2 + bx + c = 0, | (2) |
где a, b, c – произвольные вещественные числа.
Заменим в уравнении (2) переменную x на новую переменную y по формуле:
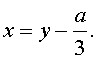 | (3) |
то уравнение (2) примет вид
В результате уравнение (2) примет вид
Если ввести обозначения
то уравнение (4) примет вид
| y 3 + py + q= 0, | (5) |
где p, q – вещественные числа.
Уравнения вида (5) и являются трёхчленными кубическими уравнениями , у которых отсутствует член со второй степенью неизвестного.
Первый этап вывода формулы Кардано завершён.
Видео:Кубические уравнения. Деление столбиком. Схема Горнера.Скачать

Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи
Следуя методу, примененому Никколо Тартальей (1499-1557) для решения трехчленных кубических уравнений, будем искать решение уравнения (5) в виде
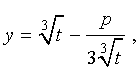 | (6) |
где t – новая переменная.
то выполнено равенство:
Следовательно, уравнение (5) переписывается в виде
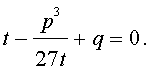 | (7) |
Если теперь уравнение (7) умножить на t , то мы получим квадратное уравнение относительно t :
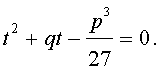 | (8) |
Видео:✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать

Формула Кардано
Решение уравнения (8) имеет вид:
В соответствии с (6), отсюда вытекает, что уравнение (5) имеет два решения:
В развернутой форме эти решения записываются так:
Покажем, что, несмотря на кажущиеся различия, решения (10) и (11) совпадают.
С другой стороны,
и для решения уравнения (5) мы получили формулу
которая и называется «Формула Кардано» .
Замечание . Поскольку у каждого комплексного числа, отличного от нуля, существуют три различных кубических корня, то, для того, чтобы избежать ошибок при решении кубических уравнений в области комплексных чисел, рекомендуется использовать формулу Кардано в виде (10) или (11).
Видео:Геометрический способ решения квадратных уравнений. Без дискриминанта!Скачать

Пример решения кубического уравнения
Пример . Решить уравнение
| x 3 – 6x 2 – 6x – 2 = 0. | (13) |
Решение . Сначала приведем уравнение (13) к трехчленному виду. Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену
| x = y + 2. | (14) |
Следовательно, уравнение (13) принимает вид
| y 3 – 18y – 30 = 0. | (15) |
Теперь в соответствии с формулой (6) сделаем в уравнении (15) еще одну замену
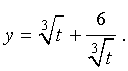 | (16) |
то уравнение (15) примет вид
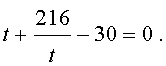 | (17) |
Далее из (17) получаем:
Отсюда по формуле (16) получаем:
Заметим, что такое же, как и в формуле (18), значение получилось бы, если бы мы использовали формулу
или использовали формулу
Далее из равенства (18) в соответствии с (14) получаем:
Таким образом, мы нашли у уравнения (13) вещественный корень
Замечание 1 . У уравнения (13) других вещественных корней нет.
Замечание 2 . Поскольку произвольное кубическое уравнение в комплексной области имеет 3 корня с учетом кратностей, то до полного решения уравнения (13) остается найти еще 2 корня. Эти корни можно найти разными способами, в частности, применив вариант формулы Кардано для области комплексных чисел. Однако применение такого варианта формулы Кардано значительно выходит за рамки курса математики даже специализированных математических школ.
Видео:Самый простой способ решить кубическое уравнениеСкачать

Решение кубических уравнений
Кубическое уравнение, содержащее коэффициенты с действительным корнем, остальные два считаются комплексно-сопряженной парой. Будут рассмотрены уравнения с двучленами и возвратные, а также с поиском рациональных корней. Вся информация будет подкреплена примерами.
Видео:КУБИЧЕСКИЕ УРАВНЕНИЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Решение двучленного кубического уравнения вида A x 3 + B = 0
Кубическое уравнение, содержащее двучлен, имеет вид A x 3 + B = 0 . Его необходимо приводить к x 3 + B A = 0 с помощью деления на А , отличного от нуля. После чего можно применять формулу сокращенного умножения суммы кубов. Получаем, что
x 3 + B A = 0 x + B A 3 x 2 — B A 3 x + B A 2 3 = 0
Результат первой скобки примет вид x = — B A 3 , а квадратный трехчлен — x 2 — B A 3 x + B A 2 3 , причем только с комплексными корнями.
Найти корни кубического уравнения 2 x 3 — 3 = 0 .
Решение
Необходимо найти х из уравнения. Запишем:
2 x 3 — 3 = 0 x 3 — 3 2 = 0
Необходимо применить формулу сокращенного умножения. Тогда получим, что
x 3 — 3 2 = 0 x — 3 3 2 6 x 2 + 3 3 2 6 x + 9 2 3 = 0
Раскроем первую скобку и получим x = 3 3 2 6 . Вторая скобка не имеет действительных корней, потому как дискриминант меньше нуля.
Ответ: x = 3 3 2 6 .
Видео:Разложение кубических выражений на множителиСкачать

Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0
Вид квадратного уравнения — A x 3 + B x 2 + B x + A = 0 , где значения А и В являются коэффициентами. Необходимо произвести группировку. Получим, что
A x 3 + B x 2 + B x + A = A x 3 + 1 + B x 2 + x = = A x + 1 x 2 — x + 1 + B x x + 1 = x + 1 A x 2 + x B — A + A
Корень уравнения равен х = — 1 , тогда для получения корней квадратного трехчлена A x 2 + x B — A + A необходимо задействовать через нахождение дискриминанта.
Решить уравнение вида 5 x 3 — 8 x 2 — 8 x + 5 = 0 .
Решение
Уравнение является возвратным. Необходимо произвести группировку. Получим, что
5 x 3 — 8 x 2 — 8 x + 5 = 5 x 3 + 1 — 8 x 2 + x = = 5 x + 1 x 2 — x + 1 — 8 x x + 1 = x + 1 5 x 2 — 5 x + 5 — 8 x = = x + 1 5 x 2 — 13 x + 5 = 0
Если х = — 1 является корнем уравнения, тогда необходимо найти корни заданного трехчлена 5 x 2 — 13 x + 5 :
5 x 2 — 13 x + 5 = 0 D = ( — 13 ) 2 — 4 · 5 · 5 = 69 x 1 = 13 + 69 2 · 5 = 13 10 + 69 10 x 2 = 13 — 69 2 · 5 = 13 10 — 69 10
Ответ:
x 1 = 13 10 + 69 10 x 2 = 13 10 — 69 10 x 3 = — 1
Видео:Формула Кардано для решения кубических уравненийСкачать

Решение кубических уравнений с рациональными корнями
Если х = 0 , то он является корнем уравнения вида A x 3 + B x 2 + C x + D = 0 . При свободном члене D = 0 уравнение принимает вид A x 3 + B x 2 + C x = 0 . При вынесении х за скобки получим, что уравнение изменится. При решении через дискриминант или Виета оно примет вид x A x 2 + B x + C = 0 .
Найти корни заданного уравнения 3 x 3 + 4 x 2 + 2 x = 0 .
Решение
3 x 3 + 4 x 2 + 2 x = 0 x 3 x 2 + 4 x + 2 = 0
Х = 0 – это корень уравнения. Следует найти корни квадратного трехчлена вида 3 x 2 + 4 x + 2 . Для этого необходимо приравнять к нулю и продолжить решение при помощи дискриминанта. Получим, что
D = 4 2 — 4 · 3 · 2 = — 8 . Так как его значение отрицательное, то корней трехчлена нет.
Ответ: х = 0 .
Когда коэффициенты уравнения A x 3 + B x 2 + C x + D = 0 целые, то в ответе можно получить иррациональные корни. Если A ≠ 1 , тогда при умножении на A 2 обеих частей уравнения проводится замена переменных, то есть у = А х :
A x 3 + B x 2 + C x + D = 0 A 3 · x 3 + B · A 2 · x 2 + C · A · A · x + D · A 2 = 0 y = A · x ⇒ y 3 + B · y 2 + C · A · y + D · A 2
Приходим к виду кубического уравнения. Корни могут быть целыми или рациональными. Чтобы получить тождественное равенство, необходимо произвести подстановку делителей в полученное уравнение. Тогда полученный y 1 будет являться корнем. Значит и корнем исходного уравнения вида x 1 = y 1 A . Необходимо произвести деление многочлена A x 3 + B x 2 + C x + D на x — x 1 . Тогда сможем найти корни квадратного трехчлена.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Необходимо произвести преобразование с помощью умножения на 2 2 обеих частей, причем с заменой переменной типа у = 2 х . Получаем, что
2 x 3 — 11 x 2 + 12 x + 9 = 0 2 3 x 3 — 11 · 2 2 x 2 + 24 · 2 x + 36 = 0 y = 2 x ⇒ y 3 — 11 y 2 + 24 y + 36 = 0
Свободный член равняется 36 , тогда необходимо зафиксировать все его делители:
± 1 , ± 2 , ± 3 , ± 4 , ± 6 , ± 9 , ± 12 , ± 36
Необходимо произвести подстановку y 3 — 11 y 2 + 24 y + 36 = 0 , чтобы получить тождество вида
1 3 — 11 · 1 2 + 24 · 1 + 36 = 50 ≠ 0 ( — 1 ) 3 — 11 · ( — 1 ) 2 + 24 · ( — 1 ) + 36 = 0
Отсюда видим, что у = — 1 – это корень. Значит, x = y 2 = — 1 2 .
Далее следует деление 2 x 3 — 11 x 2 + 12 x + 9 на x + 1 2 при помощи схемы Горнера:
| x i | Коэффициенты многочлена | |||
|---|---|---|---|---|
| 2 | — 11 | 12 | 9 | |
| — 0 . 5 | 2 | — 11 + 2 · ( — 0 . 5 ) = — 12 | 12 — 12 · ( — 0 . 5 ) = 18 | 9 + 18 · ( — 0 . 5 ) = 0 |
2 x 3 — 11 x 2 + 12 x + 9 = x + 1 2 2 x 2 — 12 x + 18 = = 2 x + 1 2 x 2 — 6 x + 9
После чего необходимо найти корни квадратного уравнения вида x 2 — 6 x + 9 . Имеем, что уравнение следует привести к виду x 2 — 6 x + 9 = x — 3 2 , где х = 3 будет его корнем.
Ответ: x 1 = — 1 2 , x 2 , 3 = 3 .
Алгоритм можно применять для возвратных уравнений. Видно, что — 1 – это его корень, значит, левая часть может быть поделена на х + 1 . Только тогда можно будет найти корни квадратного трехчлена. При отсутствии рациональных корней применяются другие способы решения для разложения многочлена на множители.
Видео:Решение уравнения третьей степени x³-9x-12=0Скачать

Решение кубических уравнений по формуле Кардано
Нахождение кубических корней возможно при помощи формулы Кардано. При A 0 x 3 + A 1 x 2 + A 2 x + A 3 = 0 необходимо найти B 1 = A 1 A 0 , B 2 = A 2 A 0 , B 3 = A 3 A 0 .
После чего p = — B 1 2 3 + B 2 и q = 2 B 1 3 27 — B 1 B 2 3 + B 3 .
Полученные p и q в формулу Кардано. Получим, что
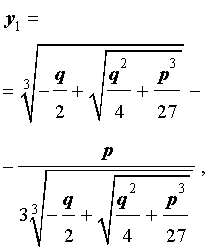
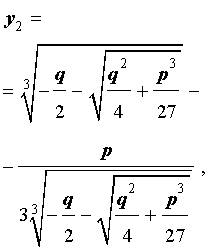
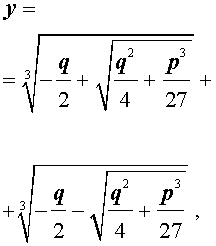
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — q 2 4 + p 3 27 3
Подбор кубических корней должен удовлетворять на выходе значению — p 3 . Тогда корни исходного уравнения x = y — B 1 3 . Рассмотрим решение предыдущего примера, используя формулу Кардано.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Видно, что A 0 = 2 , A 1 = — 11 , A 2 = 12 , A 3 = 9 .
Необходимо найти B 1 = A 1 A 0 = — 11 2 , B 2 = A 2 A 0 = 12 2 = 6 , B 3 = A 3 A 0 = 9 2 .
Отсюда следует, что
p = — B 1 2 3 + B 2 = — — 11 2 2 3 + 6 = — 121 12 + 6 = — 49 12 q = 2 B 1 3 27 — B 1 B 2 3 + B 3 = 2 · — 11 2 3 27 — — 11 2 · 6 3 + 9 2 = 343 108
Производим подстановку в формулу Кордано и получим
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — — q 2 4 + p 3 27 3 = = — 343 216 + 343 2 4 · 108 2 — 49 3 27 · 12 3 3 + — 343 216 — 343 2 4 · 108 2 — 49 3 27 · 12 3 3 = = — 343 216 3 + — 343 216 3
— 343 216 3 имеет три значения. Рассмотрим их ниже.
— 343 216 3 = 7 6 cos π + 2 π · k 3 + i · sin π + 2 π · k 3 , k = 0 , 1 , 2
Если k = 0 , тогда — 343 216 3 = 7 6 cos π 3 + i · sin π 3 = 7 6 1 2 + i · 3 2
Если k = 1 , тогда — 343 216 3 = 7 6 cosπ + i · sinπ = — 7 6
Если k = 2 , тогда — 343 216 3 = 7 6 cos 5 π 3 + i · sin 5 π 3 = 7 6 1 2 — i · 3 2
Необходимо произвести разбиение по парам, тогда получим — p 3 = 49 36 .
Тогда получим пары: 7 6 1 2 + i · 3 2 и 7 6 1 2 — i · 3 2 , — 7 6 и — 7 6 , 7 6 1 2 — i · 3 2 и 7 6 1 2 + i · 3 2 .
Преобразуем при помощи формулы Кордано:
y 1 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 + i · 3 2 + 7 6 1 2 — i · 3 2 = 7 6 1 4 + 3 4 = 7 6 y 2 = — 343 216 3 + — 343 216 3 = — 7 6 + — 7 6 = — 14 6 y 3 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 — i · 3 2 + 7 6 1 2 + i · 3 2 = 7 6 1 4 + 3 4 = 7 6
x 1 = y 1 — B 1 3 = 7 6 + 11 6 = 3 x 2 = y 2 — B 1 3 = — 14 6 + 11 6 = — 1 2 x 3 = y 3 — B 1 3 = 7 6 + 11 6 = 3
Ответ: x 1 = — 1 2 , x 2 , 3 = 3
При решении кубических уравнений можно встретить сведение к решению уравнений 4 степени методом Феррари.
📺 Видео
Решить кубическое уравнение. Два способаСкачать

Решение кубического уравнения без формул графическим методом ЛиляСкачать

РЕШЕНИЕ КУБИЧЕСКОГО УРАВНЕНИЯ МЕТОДОМ ГРУППИРОВКИСкачать

Решение кубических уравнений. Всё легко и просто!Скачать

Решение уравнений третьей степени (формула Кардано)Скачать

ФОРМУЛА КАРДАНО-ТАРТАЛЬЯ + РЕКЛАМА МФТИ!!!Скачать

Нахождение иррациональных корней кубических уравнений. Быстрый способ решения кубических уравнений.Скачать

Теорема БезуСкачать

Решение любых кубических уравнений, быстро, оригинальноСкачать