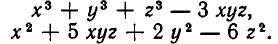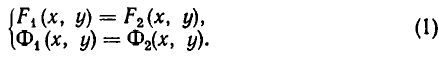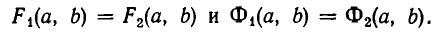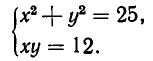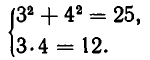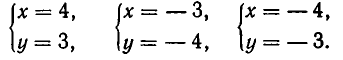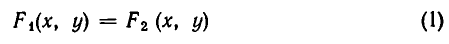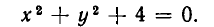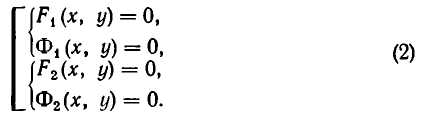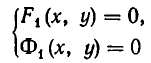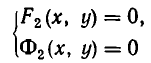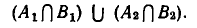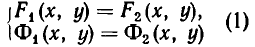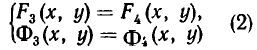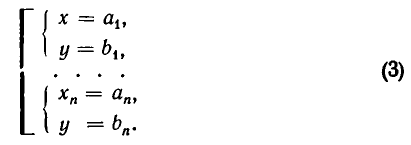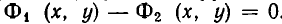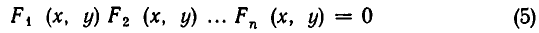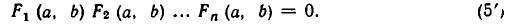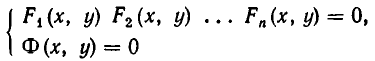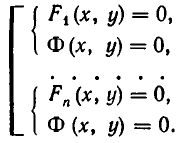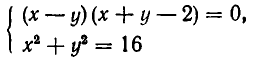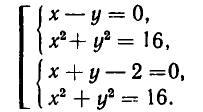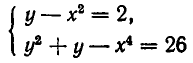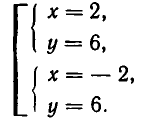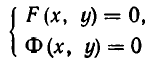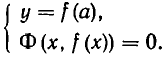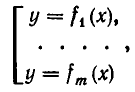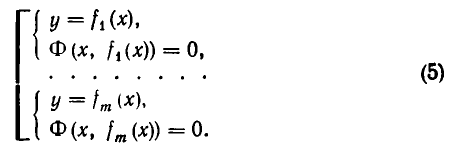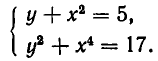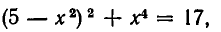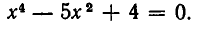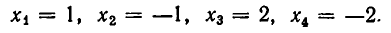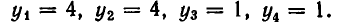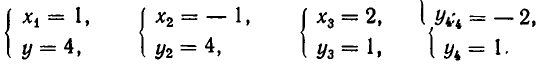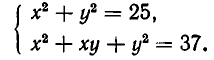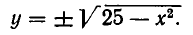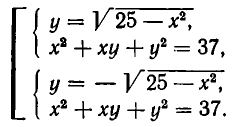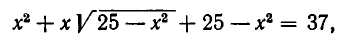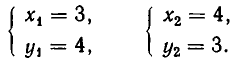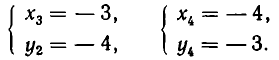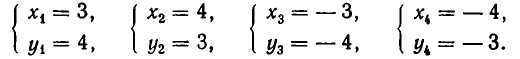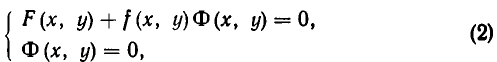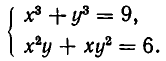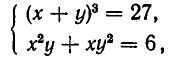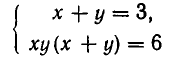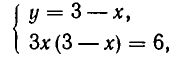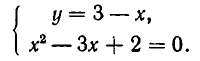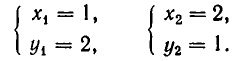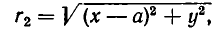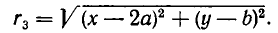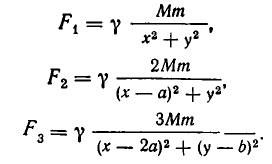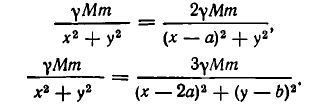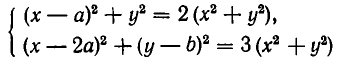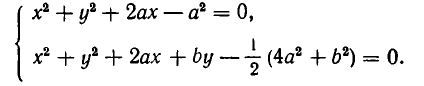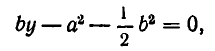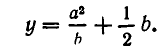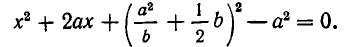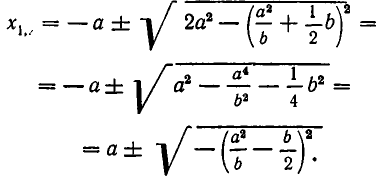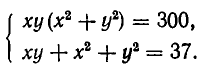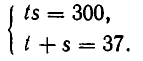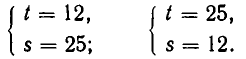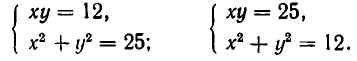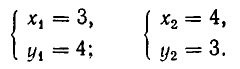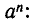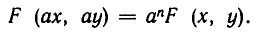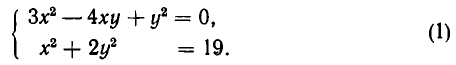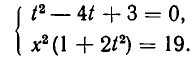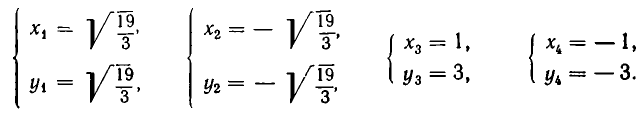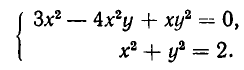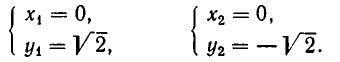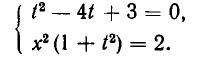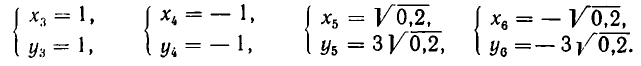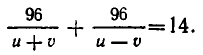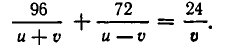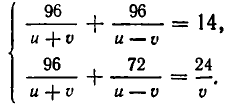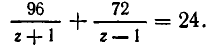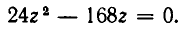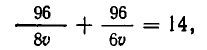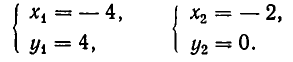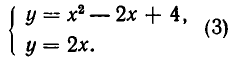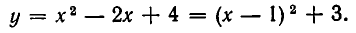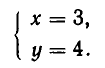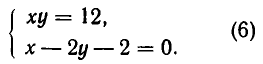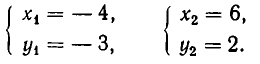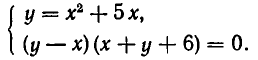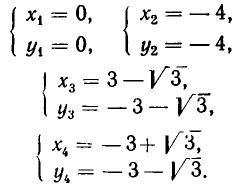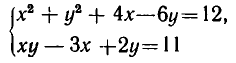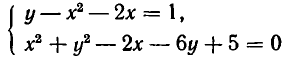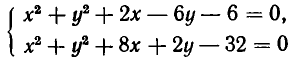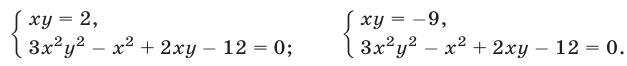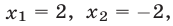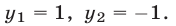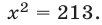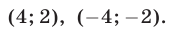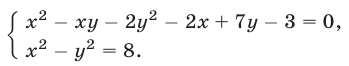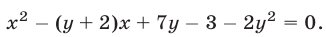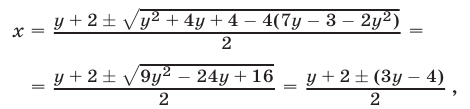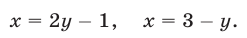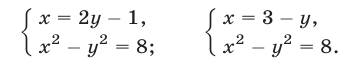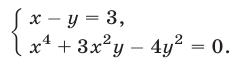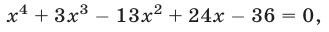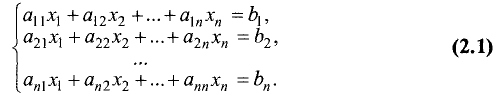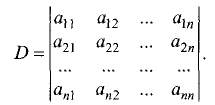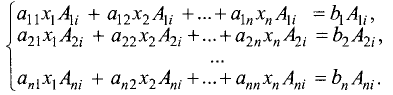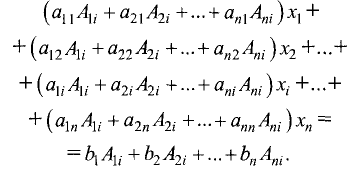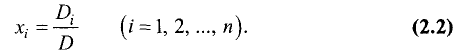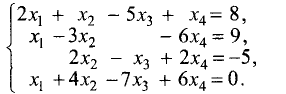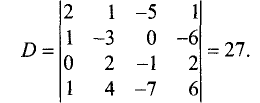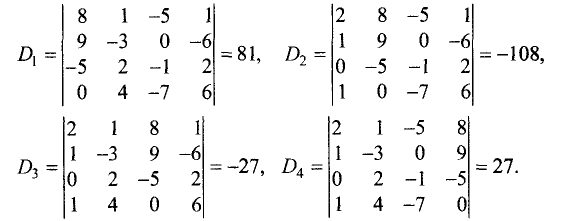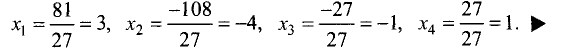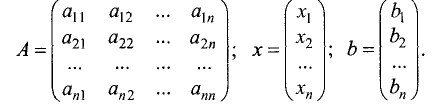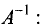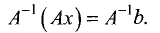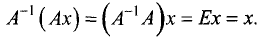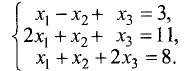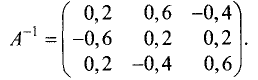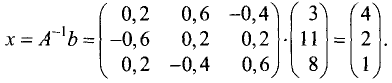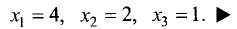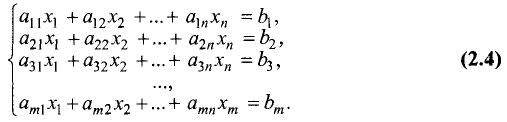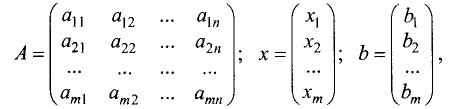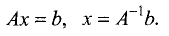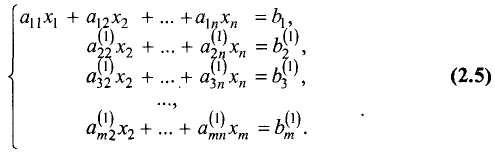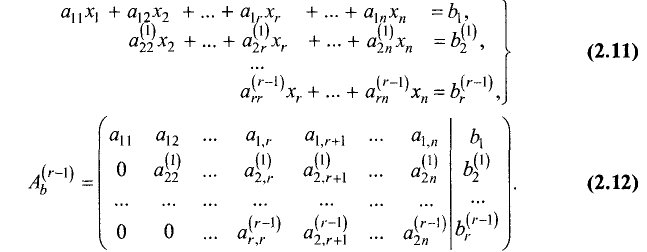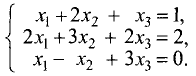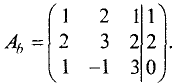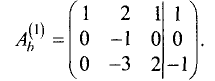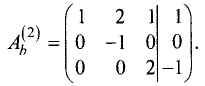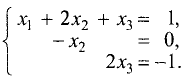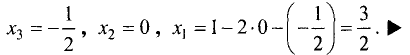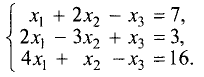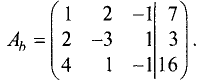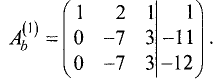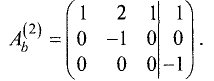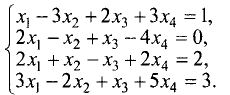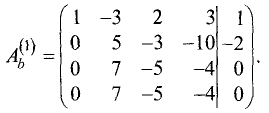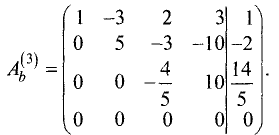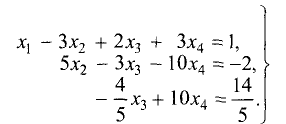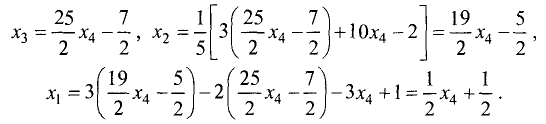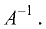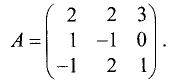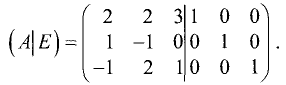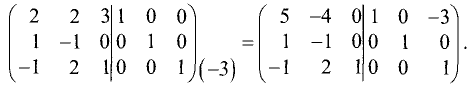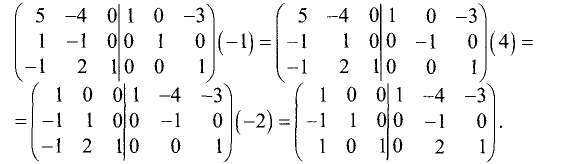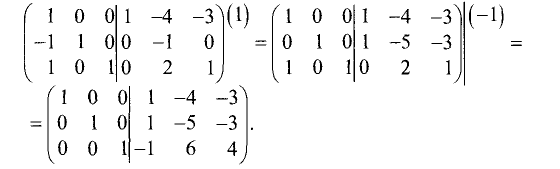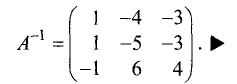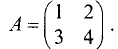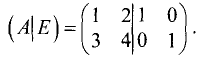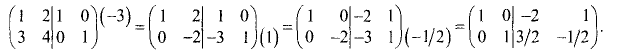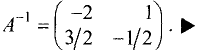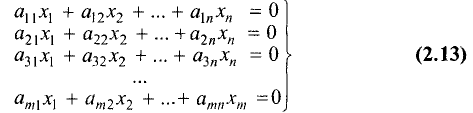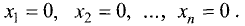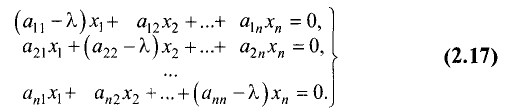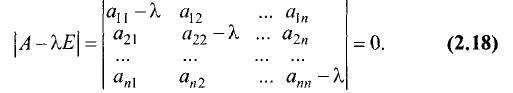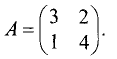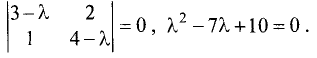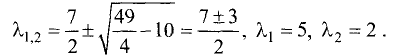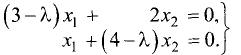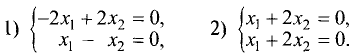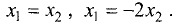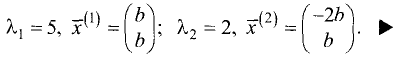- Инструменты сайта
- Основное
- Навигация
- Информация
- Действия
- Содержание
- Системы линейных уравнений
- Матричная форма записи
- Исключение переменных (метод Гаусса)
- Исключение переменных
- Установление множества решений
- Формулы Крамера
- Теорема Кронекера-Капелли
- Общее решение
- Система однородных уравнений
- Геометрическая интерпретация
- Ортогональность
- Системы алгебраических уравнений в математике с примерами решения и образцами выполнения
- Системы уравнений
- Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными
- Совокупность уравнений
- Равносильные системы уравнений
- Метод подстановки
- Метод алгебраического сложения уравнений
- Метод введения новых неизвестных
- Системы однородных уравнений
- Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными
- Решение других типов систем алгебраических систем уравнений
- Решение системы алгебраических уравнений по правилу Крамера и методом обратной матрицы
- Общий вид системы линейных алгебраических уравнений
- Решение системы линейных алгебраических уравнений методом Гаусса
- Вычисление обратной матрицы методом Гаусса
- Система линейных однородных уравнений
- Системы линейных уравнений с двумя неизвестными
- Примеры пересечения прямых
- 🎦 Видео
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Видео:Нелинейные уравнения с двумя переменными и их геометрический смысл. 9 класс.Скачать

Системы линейных уравнений
Обозначим через $ mathbb A_ $ любое из множеств $ mathbb Q_, mathbb R_ $ или $ mathbb C_ $.
Примеры систем уравнений над $ mathbb R $.
Относительно числа $ m_ $ уравнений не делается ни какого предположения: оно может быть меньше, больше или равно числу переменных $ n_ $. Если $ m_>n $ то система называется переопределенной. Решением системы уравнений называется любой набор значений переменных $ x_1=alpha_,dots, x_n = alpha_n $, обращающий каждое из уравнений в истинное равенство. Система называется совместной если она имеет хотя бы одно решение и несовместной в противном случае.
Можно доказать (см. результаты ☟ НИЖЕ ), что все возможности для произвольной системы ограничиваются следующими вариантами:
1. система совместна и имеет единственное решение;
2. cистема совместна и имеет бесконечное множество решений;
3. cистема несовместна.
При этом все решения будут находиться в том же множестве $ mathbb A_ $, что и коэффициенты системы.
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Матричная форма записи
Для системы линейных уравнений относительно переменных $ x_1,x_2,dots,x_n $ $$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_1,\ a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_2,\ dots & & & & dots \ a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_m. end right. $$ матрицей системы называется матрица $$ A=left( begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ dots &&& dots \ a_ & a_ & dots & a_ end right)_ ; $$ cтолбец $$ = left( begin b_ \ b_ \ vdots \ b_ end right) $$ называется столбцом правых частей системы, а столбец $$ X= left( begin x_ \ x_ \ vdots \ x_ end right) $$ — столбцом неизвестных. Используя правило умножения матриц, систему можно записать в матричном виде: $$ AX= . $$ Любое решение $ x_1=alpha_1,dots,x_n=alpha_n $ системы можно также записать в виде столбца: $$ X=left( begin alpha_1 \ vdots \ alpha_n end right) in mathbb A^n . $$ Матрица, составленная из всех коэффициентов системы уравнений: $$ [A mid mathcal B ]= left( begin a_ & a_ & dots & a_ & b_1 \ a_ & a_ & dots & a_ & b_2 \ dots &&& & dots \ a_ & a_ & dots & a_ & b_m end right)_ , $$ т.е. конкатенацией матрицы $ A_ $ и столбца правых частей $ _ $ называется расширенной матрицей системы л.у.
Видео:Тема: Системы линейных уравнений. Урок: Системы линейных уравнений. Геометрическая интерпретацияСкачать

Исключение переменных (метод Гаусса)
метода достаточно проста.
Пример. Решить систему уравнений $$ left< begin 2x_1&-3x_2&-x_3&=3 \ 4x_1&-3x_2&-5x_3&=6 \ 3x_1&+5x_2&+9x_3&=-8 end right. $$
Решение. Выразим из первого уравнения $ x_ $ $$ x_1=frac x_2+frac x_3 + frac $$ и подставим в оставшиеся уравнения $$ 4 left(frac x_2+frac x_3 + fracright) -3,x_2-5,x_3=6 <coloriff > 3x_2-3x_3 = 0 $$ $$ <coloriff > x_2-x_3=0 ; $$ $$ 3 left(frac x_2+frac x_3 + fracright) +5x_2+9x_3=-8 <coloriff > frac x_2 +fracx_3=-frac $$ $$ <coloriff > 19x_2 +21x_3=-25 . $$ Два получившихся уравнения не зависят от неизвестной $ x_ $ — она оказалась исключенной из этих уравнений. Иными словами, мы получили новую подсистему уравнений $$ left< begin x_2&-x_3&=0 \ 19x_2&+21x_3&=-25, end right. $$ которой должны удовлетворять неизвестные $ x_ $ и $ x_ $. Продолжаем действовать по аналогии: выразим из первого уравнения $ x_ $ через $ x_ $: $$x_2=x_3 $$ и подставим во второе: $$ 40 x_3 =-25 iff x_3=-frac . $$ Итак, значение одной компоненты решения получено. Для нахождения оставшихся подставим значение $ x_ $ в полученные по ходу решения соотношения: $$ x_2=x_3=-frac Rightarrow x_1=frac x_2+frac x_3 + frac=frac . $$
Ответ. $ x_=1/4, x_2=-5/8, x_3=-5/8 $.
Теперь осталось формализовать изложенную идею метода (сформулировав допустимые правила действия над уравнениями — те, что в принципе, очевидны из здравого смысла ), а также исследовать возможные последствия его применения к системам общего вида.
Исключение переменных
Элементарными преобразованиями системы л.у. называются преобразования следующих трех типов:
1. перестановка двух уравнений;
2. умножение обеих частей уравнения на любое отличное от нуля число;
3. прибавление к одному уравнению любого другого, умноженного на произвольное число: пара уравнений $$ begin a_x_1 +a_x_2+ ldots+a_x_n &=&b_j,\ a_x_1 +a_x_2+ ldots+a_x_n &=&b_k end $$ заменяется парой $$ begin (a_+ <colorlambda > a_) x_1 &+ (a_+ <colorlambda > a_) x_2 &+ ldots &+ (a_+ <colorlambda > a_) x_n &=&b_j + <colorlambda > b_k, , \ a_x_1 &+a_x_2&+ ldots &+a_x_n &=&b_k , . end $$
Теорема. Любое элементарное преобразование системы л.у. переводит эту систему в ей эквивалентную, т.е. имеющую то же множество решений, что и исходная.
Задача. С помощью элементарных преобразований привести систему л.у. к наиболее простому виду: такому, из которого легко было бы установить множество решений.
Предположим, что первое уравнение системы содержит явно неизвестную $ x_ $, т.е. $ a_^ ne 0 $. Исключим эту неизвестную из всех оставшихся уравнений. С этой целью вычтем из второго уравнения первое, домноженное на $ a_/a_^ $. Получим $$left(a_- frac<a_><a_> a_ right)x_2 + dots + left(a_- frac<a_><a_> a_ right)x_n = b_2 — frac<a_><a_> b_1 , $$ Аналогичное преобразование — вычитание из третьего уравнения системы первого, умноженного на $ a_/a_^ $, позволяет исключить $ x_ $ из этого уравнения, т.е. заменить его на $$left(a_- frac<a_><a_> a_ right)x_2 + dots + left(a_- frac<a_><a_> a_ right)x_n = b_3 — frac<a_><a_> b_1 . $$ Продолжаем процесс далее. В конечном итоге исключаем $ x_ $ из всех уравнений кроме первого: $$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_1,\ &a_^x_2&+ ldots&+a_^x_n &=b_2^,\ &dots & & & dots \ &a_^x_2&+ ldots&+a_^x_n &=b_m^. end right. npu begin a_^ &= & displaystyle a_ — frac<a_a_><a_> ,\ b_j^ &= & displaystyle b_j — frac<a_b_1><a_> . end $$ Полученная система эквивалентна исходной системе, однако она имеет более простой вид: в ней выделилась подсиcтема $$ left< begin a_^x_2&+ ldots&+a_^x_n &=b_2^,\ dots & & & dots \ a_^x_2&+ ldots&+a_^x_n &=b_m^, end right. $$ которая не зависит от переменной $ x_ $. К этой новой подсистеме можно применить те же рассуждения, что и к исходной системе, поставив теперь целью исключение переменной $ x_ $.
Понятно, что процесс исключения может быть продолжен и далее. Теперь посмотрим, где он может прерваться. Может так случиться, что очередная, $ ell_ $-я подсистема имеет коэффициент $ a_^ $ равным нулю, что не позволит алгоритму идти дальше — т.е. исключить переменную $ x_^ $ из оставшихся уравнений (в принципе, такое могло случиться уже на первом шаге, если бы коэффициент $ a_^ $ был бы равен нулю). Возможные варианты дальнейших действий:
1. если хотя бы один коэффициент при $ x_^ $ в одном из оставшихся уравнений отличен от нуля: $ a_^ne 0^ $, то это уравнение переставляется с $ ell_ $-м;
2. если при всех $ jge ell^ $ коэффициенты $ a_^ $ равны нулю, то переменная $ x_^ $ не входит ни в одно оставшееся уравнение, и можно перейти к исключению переменной $ x_^ $.
Поскольку число переменных конечно, то алгоритм исключения должен завершиться за конечное число шагов. Чем он может завершиться? Окончательная система должна иметь вид: $$ left< begin a_x_1 +&a_x_2&+ ldots& +a_<1 >x_& +a_ <1 ,+1>x_<+1>&+ ldots + & a_x_n &=b_1,\ &a_^x_2&+ ldots& +a_<2 >^ x_& +a_<2 ,+1>^ x_<+1>&+ ldots + & a_^ x_n &=b_2^,\ & & ddots & & & & & dots \ & & & a_ <>^<[-1]>x_ & + a_ <, +1>^<[-1]>x_<+1>& + ldots + & a_ <,n>^<[-1]>x_n &=b_^<[-1]>, \ & & & & & & 0 &=b_<+1>^<[-1]>, \ & & & & & & dots & \ & & & & & & 0 &=b_^<[-1]>, \ end right. $$ при $ le n_ $. Заметим, что все коэффициенты этой системы будут принадлежать тому же множеству, что и коэффициенты исходной системы.
Предположение . Мы будем считать, что каждое из первых $ _ $ уравнений системы содержит в своей левой части хотя бы одну переменную с ненулевым коэффициентом.
Процесс получения системы такого вида из исходной системы уравнений называется прямым ходом метода Гаусса.
Исторический комментарий о Гауссе ☞ ЗДЕСЬ.
Установление множества решений
Теорема. Если хотя бы одно из чисел $ b_<+1>^<[-1]>,dots , b_^<[-1]> $ отлично от нуля, то исходная система линейных уравнений будет несовместной.
Для простоты мы будем иллюстрировать наши рассуждения на системах л.у. над $ mathbb R_ $, в этом же множестве искать решения. Каждое из преобразований метода Гаусса будем обозначать $ to_ $.
Пример. Решить систему л.у.
$$ left< begin x_1&+x_2&-3, x_3 =& -1 \ 2,x_1&+x_2&-2, x_3 =& 1 \ x_1&+x_2&+ x_3 =& 3 \ x_1&+2,x_2&-3, x_3 =& 1. end right. $$
Решение. $$ to left< begin x_1&+x_2&-3, x_3 =& -1 \ &-x_2&+4, x_3 =& 3 \ &&4, x_3 =& 4 \ &x_2&=& 2 end right. to left< begin x_1&+x_2&-3, x_3 =& -1 \ &-x_2&+4, x_3 =& 3 \ &&4, x_3 =& 4 \ &&4, x_3=& 5 end right. to $$ $$ to left< begin x_1&+x_2&-3, x_3 =& -1 \ &-x_2&+4, x_3 =& 3 \ &&4, x_3 =& 4 \ &&0=& 1 end right. $$ Последнее равенство абсолютно противоречиво.
Ответ. Система несовместна.
Пусть теперь $ b_<+1>^<[-1]>=0,dots, b_^<[-1]>=0 $. Возможны два случая: $ =n_ $ и $ предположения , имеем $ a_^ ne 0 $. Но тогда, поскольку система является конечной стадией прямого хода метода Гаусса, то и все коэффициенты $ a_^, dots, a_^, a_ $ должны быть отличны от нуля — в противном случае метод Гаусса не остановился бы на системе такого вида; он называется треугольным: 
Теорема. Если прямой ход метода Гаусса заканчивается треугольной системой, т.е. $ mathfrak r = n_ $ и $ b_<+1>^<[-1]>=0,dots, b_^<[-1]>=0 $, то исходная система линейных уравнений имеет единственное решение.
Пример. Решить систему л.у.
$$ left< begin x_1&+3,x_2&+ x_3 =&5 \ 2,x_1&+x_2&+ x_3 =& 2 \ x_1&+x_2&+ 5,x_3 =& -7 \ 2,x_1&+3,x_2&-3, x_3 =& 14. end right. $$
Ответ. $ x_1=1,, x_=2,, x_3=-2 $ .
Исследуем теперь случай $ 1) : 
Теорема. Если прямой ход метода Гаусса заканчивается трапециевидной системой, т.е. $ mathfrak r 2) матрицы $ A_ $ (третьего порядка). Понятие определителя распространяется и на квадратные матрицы бóльших порядков; образно говоря, определитель — это функция элементов матрицы, отвечающая за единственность решения системы уравнений.
Дальнейший матричный анализ метода Гаусса ☞ ЗДЕСЬ.
Видео:Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Формулы Крамера
Рассмотрим систему линейных уравнений с квадратной матрицей $ A_ $, т.е. такую, у которой число уравнений совпадает с числом неизвестных.
Теорема. Cистема
$$ left<begin a_x_1 +a_x_2+ldots+a_x_n &=&b_1\ a_x_1 +a_x_2+ldots+a_x_n &=&b_2\ ldots& & ldots \ a_x_1 +a_x_2+ldots+a_x_n &=&b_n endright. $$ имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля: $$ left| begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ dots &&& dots \ a_ & a_ & dots & a_ end right| ne 0 . $$ В этом случае решение можно вычислить по формулами Крамера 3) : $$ x_k =frac<det left[ A_|dots|A_||A_|dots|A_ right]> quad npu quad kin . $$ Для получения значения $ x_ $ в числитель ставится определитель, получающийся из $ det A_ $ заменой его $ k_ $-го столбца на столбец правых частей ( здесь $ | $ означает конкатенацию).
Доказательство ☞ ЗДЕСЬ
Пример. Решить систему уравнений
$$ left<begin 2x_1& +3x_2&+11x_3&+5x_4 &=& color2,\ x_1& +x_2&+5x_3&+2x_4 &=& color1 ,\ 2x_1& +x_2&+3x_3&+2x_4 &=&color,\ x_1& +x_2&+3x_3&+4x_4 &=&color. endright. $$
Решение. $$ x_1=frac<left|begin color2 & 3&11&5 \ color1 & 1&5&2 \ color& 1&3&2 \ color & 1&3&4 endright|> <left|begin 2& 3&11&5 \ 1& 1&5&2 \ 2& 1&3&2 \ 1& 1&3&4 endright|>=frac=-2, x_2=frac<left|begin 2& color2&11&5 \ 1& color1&5&2 \ 2& color&3&2 \ 1& color&3&4 endright|> <left|begin 2& 3&11&5 \ 1& 1&5&2 \ 2& 1&3&2 \ 1& 1&3&4 endright|>=frac=0, dots $$ Найдите оставшиеся компоненты решения. ♦
Решение системы линейных уравнений с квадратной матрицей $ A_ $ является непрерывной функцией коэффициентов этой системы при условии, что $ det A_ ne 0 $.
Кроме того, формулы Крамера начинают конкурировать по вычислительной эффективности с методом Гаусса в случае систем, зависящих от параметра. Подробнее ☞ ЗДЕСЬ.
Еще один способ решения системы основан на построении обратной матрицы: $$ AX= quad Rightarrow quad X=A^ . $$ Этот способ малоэффективен при фиксированных числовых $ A_ $ и $ _ $.
Найти достаточное условие существования общего решения систем уравнений:
$$ A_1 X = _1 quad u quad A_2 Y = _2 , $$ при квадратных матрицах $ A_1 $ и $ A_2 $ одинакового порядка.
Видео:ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

Теорема Кронекера-Капелли
Матрица, получающаяся конкатенацией матрицы $ A_ $ и столбца правых частей $ _ $ $$ [ A| ] = left( begin a_ & a_ & dots & a_ & b_1 \ a_ & a_ & dots & a_ & b_2 \ dots &&& & dots \ a_ & a_ & dots & a_ & b_m end right)_ $$ называется расширенной матрицей системы линейных уравнений $ AX= $.
Теорема [Кронекер, Капелли]. Система $ AX= $ совместна тогда и только тогда, когда ранг матрицы этой системы совпадает с рангом ее расширенной матрицы:
$$ operatorname, A = operatorname, [ A| ] . $$ При выполнении этого условия, система имеет единственное решение, если число неизвестных $ n_ $ совпадает с общим значением ранга $ mathfrak r_ $, и бесконечное множество решений, если $ n_ $ больше этого значения.
Доказательство необходимости. Пусть существует решение $ x_1=alpha_1,dots,x_n=alpha_n $ системы, тогда $$alpha_1 A_+dots+alpha_n A_= ,$$ т.е. столбец $ $ линейно выражается через столбцы $ A_,dots,A_ $. Но тогда $$ operatorname <A_,dots,A_>=operatorname <A_,dots,A_,> .$$ Следовательно $ operatorname, A = operatorname, [ A| ] $.
Доказательство достаточности проводится в следующем пункте. ♦
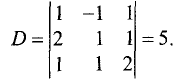
Пример. Исследовать совместность системы уравнений
Решение. В этом примере число уравнений совпадает с числом неизвестных. Это обстоятельство несколько облегчает рассуждения. Обратимся к замечанию из предыдущего пункта: система л.у. с числом уравнений, совпадающем с числом неизвестных, как правило, совместна. Тогда попробуем установить условия, обеспечивающие противоположное свойство — несовместность. Оно, фактически, единственно: за все отвечает определитель системы $ det A_ $. Если он отличен от нуля — система совместна. $$det A = left| begin<color> &1&1&1 \ 1&<color>&1&1 \ 1&1&<color>&1 \ 1&1&1&<color> end right|= left| begin (<color>-1) &(1-<color>)&0&0 \ 0&(<color>-1)&(1-<color>)&0 \ 0&0&(<color>-1)&(1-<color>) \ 1&1&1&<color> end right| =(<color>-1)^3 left| begin 1 &-1&0&0 \ 0&1&-1&0 \ 0&0&1&-1 \ 1&1&1&<color> end right|= $$ $ =(<color>-1)^3(<color>+3) $. По теореме Крамера при $ <color>ne 1 $ и при $ <color>ne -3 $ решение системы единственно: $$x_1=x_2=x_3=x_4=1/(<color>+3) .$$
Осталось исследовать критические случаи: $ <color>=1_ $ и $ <color>= -3 $: определитель системы обращается в нуль, но система может оказаться совместной. Придется вычислять ранги, но, к счастью, уже числовых матриц (а не зависящих от параметра, как исходная!). При $ <color>= 1_ $ имеем $$ operatorname left( begin 1 &1&1&1 \ 1&1&1&1 \ 1&1&1&1 \ 1&1&1&1 end right)= operatorname left( begin 1&1&1&1&1 \ 1&1&1&1&1 \ 1&1&1&1&1 \ 1&1&1&1&1 end right)=1 , $$ и система совместна. Она эквивалентна единственному уравнению $$x_1+x_2+x_3+x_4=1 ,$$ которое имеет бесконечно много решений.
При $ <color>= -3 $: $$ operatorname left( begin -3 &1&1&1 \ 1&-3&1&1 \ 1&1&-3&1 \ 1&1&1&-3 end right)=3,quad operatorname left( begin -3 &1&1&1&1 \ 1&-3&1&1&1 \ 1&1&-3&1&1 \ 1&1&1&-3&1 end right)=4 $$ и система несовместна.
Ответ. Система несовместна при $ <color> = -3 $; она имеет бесконечное множество решений при $ <color> = 1_ $ и единственное решение при $ <color> notin $.
Система однородных уравнений
$$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ dots & & & dots & \ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0 end right. $$ всегда совместна: она имеет тривиальное решение $ x_1=0,dots,x_n=0 $. Для того, чтобы у нее существовало еще и нетривиальное решение необходимо и достаточно, чтобы определитель ее матрицы был равен нулю.
Пример. Найти условие, при котором три точки плоскости с координатами $ (x_1,y_1), (x_2,y_2) $ и $ (x_3,y_) $ лежат на одной прямой.
Решение. Будем искать уравнение прямой в виде $ ax+by+c=0 $ при неопределенных коэффициентах $ a,b,c_ $. Если точки лежат на прямой, то получаем для определения этих коэффициентов систему линейных уравнений: $$ left< begin ax_1+by_1+c & =0\ ax_2+by_2+c & =0\ ax_3+by_3+c & =0 end right. $$ Получившаяся система является однородной, условие существования у нее нетривиального решения (т.е. набора $ (a,b,c)_ $ при хотя бы одном из чисел отличном от нуля): $$ left|begin x_1 & y_1 & 1 \ x_2 & y_2 & 1 \ x_3 & y_3 & 1 end right|=0 . $$ ♦
Доказать, что для совместности системы
$$ left< begin a_x_1+a_x_2+a_x_3 &=& b_1 \ a_x_1+a_x_2+a_x_3 &=& b_2 \ a_x_1+a_x_2+a_x_3 &=& b_3 \ a_x_1+a_x_2+a_x_3 &=& b_4 end right. $$ необходимо, чтобы было выполнено условие $$ left| begin a_&a_& a_ & b_1 \ a_&a_& a_ & b_2 \ a_&a_& a_ & b_3 \ a_&a_& a_ & b_4 end right|=0 quad . $$ Является ли это условие достаточным для совместности?
An elementary treatise on determinants
в следующей формулировке.
Теорема. Для того чтобы система $ n_ $ неоднородных уравнений была совместна, необходимо и достаточно, чтобы порядок наибольшего отличного от нуля минора был одинаков в расширенной и нерасширенной матрице системы.
Додсон — один из самых знаменитых математиков мира. Назовите его псевдоним.
Ответ ☞ ЗДЕСЬ
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Общее решение
Пусть выполнено условие теоремы Кронекера-Капелли: $ operatorname (A)=operatorname[Amid mathcal B ] =mathfrak $. По определению ранга матрицы, в матрице $ A $ существует минор порядка $ mathfrak $, отличный от нуля; этот же минор останется и минором расширенной матрицы $ [ Amid mathcal B ] $. Пусть, для определенности, ненулевой минор находится в левом верхнем углу матрицы 4) : $$ Delta = Aleft( begin 1 & 2 & dots & mathfrak \ 1 & 2 & dots & mathfrak end right) = left| begin a_ & a_ & dots & a_<1mathfrak> \ a_ & a_ & dots & a_<2mathfrak> \ dots &&& dots \ a_<mathfrak1> & a_<mathfrak2> & dots & a_ <mathfrakmathfrak> end right| ne 0 . $$ Тогда первые $ mathfrak $ строк матрицы $ A $ линейно независимы, а остальные будут линейно выражаться через них. Это же утверждение будет справедливо и для строк матрицы $ [Amid mathcal B] $. Умножая первые $ mathfrak $ уравнений системы на соответствующие числа и складывая их, получим любое оставшееся уравнение. Таким образом, система уравнений может быть заменена эквивалентной ей системой из первых $ mathfrak $ уравнений: $$ left< begin a_x_1+dots+a_<1mathfrak>x_<mathfrak>&+a_<1,mathfrak+1>x_<mathfrak+1>+ dots +a_x_n&=&b_1, \ dots & & & dots \ a_<mathfrak1>x_1+dots+a_<mathfrakmathfrak>x_<mathfrak>& +a_<mathfrak,mathfrak+1>x_<mathfrak+1>+dots +a_<mathfrakn>x_n&=&b_mathfrak end right. quad iff quad A^ X=^ $$ Если $ mathfrak=n $, то матрица $ A^ $ квадратная. По предположению $ det A^ ne 0 $. По теореме Крамера решение такой системы единственно.
Пусть теперь $ mathfrak произвольных фиксированных значениях $ x_<mathfrak+1>,dots,x_n $: $$ x_j=frac< left| begin a_ & dots &a_ &left[ b_1-(a_<1,mathfrak+1>x_<mathfrak+1>+dots +a_x_n) right] &a_& dots &a_<1mathfrak> \ dots &&&dots&&& dots \ a_<mathfrak1> & dots &a_<mathfrak,j-1> & left[ b_<mathfrak>- (a_<mathfrak,mathfrak+1>x_<mathfrak+1>+dots +a_<mathfrakn>x_n) right] &a_<mathfrak,j+1>& dots &a_<mathfrakmathfrak> end right| > $$ $$ mbox jin <1,dots, mathfrak> . $$ Таким образом, в этом случае система имеет бесконечное множество решений. Используя свойство линейности определителя по столбцу (см. свойство 5 ☞ ЗДЕСЬ ), формулы можно переписать в виде $$ x_j=beta_j + gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> . $$ Здесь $$ beta_j =frac left| begin a_ & dots &a_ & b_1 &a_& dots &a_<1mathfrak> \ vdots &&&vdots&&& vdots \ a_<mathfrak1> & dots &a_<mathfrak,j-1> & b_<mathfrak> &a_<mathfrak,j+1>& dots &a_<mathfrakmathfrak> end right|, , $$ $$ gamma_ = -frac left| begin a_ & dots &a_ & a_ &a_& dots &a_<1mathfrak> \ vdots &&&vdots&&& vdots \ a_<mathfrak1> & dots &a_<mathfrak,j-1> & a_<mathfrakk> &a_<mathfrak,j+1>& dots &a_<mathfrakmathfrak> end right| . $$ Эти формулы называются общим решением системы $ A X=mathcal B $. Участвующие в них переменные $ x_<mathfrak+1>,dots,x_n $ называются основными (или свободными), а $ x_1,dots,x_<mathfrak> $ — зависимыми. Решение, получающееся из общего решения фиксированием значений основных переменных, называется частным решением системы уравнений.
Пример. Исследовать совместность и найти общее решение системы уравнений:
Решение проведем двумя способами, соответствующими двум способам вычисления ранга матрицы. Вычисляем сначала ранг матрицы $ A $ по методу окаймляющих миноров: $$ |2| ne 0,quad left| begin 2 & 1 \ 6 & 2 end right| ne 0, quad left| begin 2 & 1 & 2 \ 6 & 2 & 4 \ 4 & 1 & 1 end right|=2 ne 0 , $$ а все миноры, окаймляющие последний, равны нулю. Итак, $ operatorname (A) =3 $. Для нахождения ранга расширенной матрицы $ [Amid mathcal B] $ достаточно проверить окаймление найденного ненулевого минора третьего порядка с помощью элементов взятых из столбца правых частей. Имеется всего один такой минор, и он равен нулю. Следовательно $ operatorname[ Amid mathcal B ] =3 $, система совместна, и имеет бесконечное множество решений.
Ненулевой минор третьего порядка (базисный минор) находится в первой, второй и четвертых строках, что означает линейную независимость соответствующих уравнений. Третье уравнение линейно зависит от остальных, и может быть отброшено. Далее, указанный базисный минор образован коэффициентами при $ x_1,x_3 $ и $ x_4 $. Следовательно оставшиеся уравнения могут быть разрешены относительно этих переменных, т.е. они — зависимые, а $ x_2 $ и $ x_5 $ — основные. Использование формулы дает общее решение $$ begin x_1&=&frac<left| begin 2 & 1 & 2 \ 3 & 2 & 4 \ 1 & 1 & 1 end right|> -x_2frac<left| begin -1 & 1 & 2 \ -3 & 2 & 4 \ -2 & 1 & 1 end right|> -x_5frac<left| begin 3 & 1 & 2 \ 5 & 2 & 4 \ 2 & 1 & 1 end right|> =-frac+fracx_2+fracx_5, \ & & \ x_3&=&frac<left| begin 2 & 2 & 2 \ 6 & 3 & 4 \ 4 & 1 & 1 end right|> -x_2frac<left| begin 2 & -1 & 2 \ 6 & -3 & 4 \ 4 & -2 & 1 end right|> -x_5frac<left| begin 2 & 3 & 2 \ 6 & 5 & 4 \ 4 & 2 & 1 end right|>=3-4x_5, \ & & \ x_4 &=&frac<left| begin 2 & 1 & 2 \ 6 & 2 & 3 \ 4 & 1 & 1 end right|> -x_2frac<left| begin 2 & 1 & -1 \ 6 & 2 & -3 \ 4 & 1 & -2 end right|> -x_5frac<left| begin 2 & 1 & 3 \ 6 & 2 & 5 \ 4 & 1 & 2 end right|> = 0. end $$ Решим теперь ту же задачу, воспользовавшись методом Гаусса исключения переменных в системе линейных уравнений: $$ left< begin 2x_1&-x_2&+x_3&+2x_4&+3x_5&=&2, \ &&x_3&+2x_4&+4x_5&=&3, \ &&&x_4&&=&0 end right. $$ Используя обратный ход метода Гаусса, снова приходим к полученным формулам.
Ответ. Общее решение системы: $ x_1=1/2 (x_2+x_5-1), x_3=3-4,x_5, x_4=0 $.
Проанализируем теперь полученные общие формулы для общего решения. В этих формулах $ beta_j $ представляет решение системы, получаемое при $ x_<mathfrak+1>=0,dots,x_n=0 $. Величины же коэффициентов $ gamma_ $ вовсе не зависят от правых частей системы и будут одинаковыми при любых значениях $ b_1,dots,b_m $. В частности, если $ b_1=0,dots,b_m=0 $, то в формулах величины $ beta_j $ обращаются в нуль и эти формулы превращаются в $$ x_j=gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> . $$
Вывод. Формула общего решения системы $ A X=mathcal B $: $$ x_j=beta_j + gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> $$ состоит из двух частей: слагаемые, не содержащие свободных переменных, определяют частное решение неоднородной системы: $$ x_1= beta_1,dots, x_<mathfrak>= beta_<mathfrak>,x_<mathfrak+1>=0,dots,x_n=0 ; $$ оставшиеся после их отбрасывания формулы задают общее решение системы $ AX=mathbb O $. Этот результат обобщается в следующей теореме.
Теорема. Общее решение системы уравнений $ A X=mathcal B $ представимо в виде суммы какого-то частного решения этой системы и общего решения соответствующей однородной системы $ A X=mathbb O $.
Доказательство тривиально если система $ A X=mathcal B $ имеет единственное решение. Если же решений бесконечно много, то выбрав какое-то одно частное $ X=X_1 $ мы получаем, что любое другое частное решение $ X=X_2 $ должно быть связано с первым соотношением $$ A(X_2-X_1)=mathbb O , $$ т.е. разность частных решений неоднородной системы обязательно является решением однородной системы уравнений $ AX=mathbb O $. ♦
Теперь посмотрим как можно описать общее решение однородной системы.
Система однородных уравнений
Система линейных уравнений называется однородной, если все коэффициенты правых частей равны нулю: $$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ dots & & & dots & \ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0. end right. $$ или, в матричном виде: $$ A_X=_ $$
Задача ставится о поиске нетривиального решения. Оно не всегда существует. Так, к примеру, если матрица $ A_ $ системы — квадратная и имеет ненулевой определитель, то, согласно теореме Крамера, нетривиальных решений у однородной системы нет. Теорема Кронекера-Капелли утверждает, что условие $ det (A_) = 0 $ является и достаточным для существования нетривиального решения.
Теорема 1. Для того, чтобы система однородных уравнений с квадратной матрицей $ A_ $ имела нетривиальное решение необходимо и достаточно, чтобы $ det (A_) = 0 $.
Для произвольной (не обязательно квадратной) матрицы $ A_ $ имеет место следующий общий результат.
Теорема 2. Если $ operatorname (A)=mathfrak r 5) $ A_^ $.
Теорема 3. Множество решений системы однородных уравнений образует линейное подпространство пространства $ mathbb A^ $. Размерность этого подпространства равна $ n-mathfrak r $, а фундаментальная система решений образует его базис.
Пусть матрица системы $ AX=mathbb O $ квадратная и
$$ operatorname (A) =n_-1 , .$$ Доказать, что если ненулевой минор матрицы порядка $ n_-1 $ соответствует какому-нибудь элементу $ j_ $-й строки, то система алгебраических дополнений к элементам $ a_,dots,a_^ $ этой строки составляет ФСР для $ AX=mathbb O_ $. Например, для системы $$ left< begin a_x_1 +a_x_2+a_x_3&=0,\ a_x_1 +a_x_2+a_x_3&=0 end right. $$ ФСР состоит из решения $$ x_1=left| begin a_ & a_ \ a_ & a_ end right| , x_2=-left| begin a_ & a_ \ a_ & a_ end right| , x_3=left| begin a_ & a_ \ a_ & a_ end right| , $$ если только хотя бы один из миноров отличен от нуля.
Теперь обсудим способы нахождения ФСР.
1. Первый из них получается из общего метода решения системы линейных уравнений, рассмотренного в предыдущем пункте. Так же, как и в том пункте, сделаем упрощающее обозначения предположение, что зависимыми переменными являются первые $ x_,dots,x_ $, т.е. общее решение задается формулами $$ x_j=gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> . $$ Иными словами, вектор столбец $$ X=left(begin gamma_<1,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n \ gamma_<2,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n \ vdots \ gamma_<mathfrak,mathfrak+1>x_<mathfrak+1>+dots+gamma_<mathfrakn>x_n \ x_<mathfrak+1> \ x_<mathfrak+2> \ vdots \ x_ endright) $$ будет решением однородной системы при любых наборах значений основных переменных $ x_<mathfrak+1>,dots,x_ $. Представим этот вектор в виде суммы векторов: $$ =x_<mathfrak+1> underbrace< left(begin gamma_<1,mathfrak+1> \ gamma_<2,mathfrak+1> \ vdots \ gamma_<mathfrak,mathfrak+1> \ 1 \ 0 \ vdots \ 0 endright)>_ + x_<mathfrak+2> underbrace<left(begin gamma_<1,mathfrak+2> \ gamma_<2,mathfrak+2> \ vdots \ gamma_<mathfrak,mathfrak+2> \ 0 \ 1 \ vdots \ 0 endright)>_+dots+ x_ underbrace<left(begin gamma_ \ gamma_ \ vdots \ gamma_<mathfrakn> \ 0 \ 0 \ vdots \ 1 endright)>_<X_> . $$ Таким образом, любое решение однородной системы представимо в виде линейной комбинации $ n_- mathfrak r $ фиксированных решений. Именно эти решения и можно взять в качестве ФСР — их линейная независимость очевидна (единицы в нижних частях каждого вектора $ X_ $ расположены на разных местах, и ни какая линейная комбинация столбцов $ < X_1,dots,X_> $ не сможет обратить их одновременно в нуль).
Оформим этот способ построения ФСР в теорему:
Теорема 4. Если система уравнений $ AX=mathbb O $ имеет структуру матрицы $ A_ $ вида:
$$ A = left[ E_ mid P_ right] , $$ то ее ФСР состоит из столбцов матрицы $$ left[ begin — P^ \ hline E_ end right] . $$
Пример. Найти ФСР для системы уравнений
Решение. Приводим систему к трапециевидному виду: $$ left< begin x_1-&x_2+&x_3-&x_4=&0, \ &&x_3+&4x_4=&0 end right. $$ В качестве зависимых переменных можно взять, например, $ x_ $ и $ x_ $. $$ begin x_1 & x_3 & x_2 & x_4 \ hline 1 & 0 & 1 & 0 \ 5 & -4 & 0 & 1 end $$
2. Этот способ напоминает вычисление обратной матрицы методом приписывания единичной матрицы. Транспонируем матрицу $ A_ $ системы и припишем к ней справа единичную матрицу порядка $ n_ $: $$ left[ A^ | E_n right] = left(begin a_ & a_ & dots & a_ & 1 & 0 & 0 & dots & 0 \ a_ & a_ & dots & a_ & 0 & 1 & 0 & dots & 0 \ a_ & a_ & dots & a_ & 0 & 0 & 1 & dots & 0 \ vdots & & & vdots & vdots & & & ddots & vdots \ a_ & a_ & dots & a_ & 0 & 0 & 0 & dots & 1 end right) ; $$ здесь $ |_ $ означает конкатенацию. Получившуюся матрицу элементарными преобразованиями строк приводим к форме: $$ left( begin hat A & K \ mathbb O & L end right) = left(begin color & * & * & dots & * & * & * & * & * & * & * & dots & * \ 0 & color & * & dots & * & * & * & * & * & * & * & dots & * \ 0 & 0 & color & dots & * & * & * & * & * & * & * & dots & * \ vdots & & & ddots & & vdots & & & vdots & & & & vdots \ 0 & 0 & dots & & 0 & color & * & * & * & * & * & dots & * \ hline 0 & 0 & dots & 0 & 0 & 0 & 0 & 0 & Box & Box & Box & dots & Box \ vdots & & & & & vdots & & & vdots & & & & vdots \ 0 & 0 & dots & 0 & 0 & 0 & 0 & 0 & Box & Box & Box & dots & Box end right) begin left.begin \ \ \ \ \ endright> mathfrak r \ left. begin \ \ \ endright> n — mathfrak r end . $$ Элементы трапециевидной матрицы $ hat A $, обозначенные $ color $, могут быть равны нулю, но $ operatorname(hat A)= mathfrak r_ $. В этом случае строки матрицы $ L_ $, образовавшейся в правом нижнем углу (ее элементы обозначены $ Box $), составляют ФСР для системы $ AX=mathbb O $.
Пример. Найти ФСР для системы уравнений
$$ left< begin x_1 &+2,x_2&+ x_3&+3,x_4&-x_5&+2,x_6=&0,\ -3x_1 &-x_2&+ 2,x_3&-4,x_4&+x_5&-x_6=&0,\ x_1 &+x_2&+ 3,x_3&+2,x_4&+x_5&+3,x_6=&0,\ -8,x_1 &-7,x_2&+ 4,x_3&-15,x_4&+6,x_5&-5,x_6=&0,\ 6x_1 &+5,x_2& +5,x_3&+11,x_4 &&+9,x_6=&0. end right. $$ Решение. Преобразуем матрицу $ left[ A^ | E_6 right] $
$$ left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 2 & -1 & 1 & -7 & 5 & & 1 \ 1 & 2 & 3 & 4 & 5 & & & 1 \ 3 & -4 & 2 & -15 & 11 &&&& 1 \ -1 & 1 & 1 & 6 & 0 &&&&& 1 \ 2 & -1 & 3 & -5 & 9 &&&&&& 1 end right)_ $$ к трапециевидной форме с помощью элементарных преобразований строк: $$ rightarrow left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 0 & 5 & -1 & 9 & -7 &-2 & 1 \ 0 & 5 & 2 & 12 & -1 &-1 &0 & 1 \ 0 & 5 & -1 & 9 & -7 &-3&0&0& 1 \ 0 & -2 & 2 & -2 & 6 &1&0&0&0& 1 \ 0 & 5 & 1 & 11 & -3 &-2&0&0&0&0& 1 end right)rightarrow $$ $$ rightarrow left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 0 & 5 & -1 & 9 & -7 &-2 & 1 \ 0 & 0 & 3 & 3 & 6 &1 &-1 & 1 \ 0 & 0 & 0 & 0 & 0 &-1&-1&0& 1 \ 0 & 0 & 8/5 & 8/5 & 16/5 &1/5&2/5&0&0& 1 \ 0 & 0 & 2 & 2 & 4 &0&-1&0&0&0& 1 end right)rightarrow $$ $$ rightarrow left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 0 & 5 & -1 & 9 & -7 &-2 & 1 \ 0 & 0 & 3 & 3 & 6 &1 &-1 & 1 \ 0 & 0 & 0 & 0 & 0 &-1&-1&0& 1 \ 0 & 0 & 0 & 0 & 0 &-1/3&14/15&-8/15&0& 1 \ 0 & 0 & 0 & 0 & 0 &-2/3&-1/3&-2/3&0& 0 & 1 end right) $$
3. Еще один способ построения ФСР основан на теореме Гамильтона-Кэли.
Теорема. Пусть матрица системы $ AX=mathbb O $ квадратная и $ operatorname (A) = $. Тогда характеристический полином матрицы $ A_ $ имеет вид:
Пример. Найти ФСР для системы уравнений
Решение. Здесь $$ A= left( begin 1 & 1 & -1 & -1 \ 2 & 3 & 1 & -2 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 end right), quad det (A-lambda E) = lambda^2(lambda^2-4lambda+1), $$ $$ A^2-4A+E= left( begin 0 & 0 & 4 & 1 \ 0 & 0 & -3 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 end right) $$
Блок-схемы зависимости множества решений системы уравнений $ AX= mathcal B $ от комбинации чисел $ n, mathfrak r $ ☞ ЗДЕСЬ.
Видео:Решение системы уравнений методом Крамера 2x2Скачать

Геометрическая интерпретация
Геометрический смысл введенных определений поясним на примере $ mathbb R^ $. Уравнение $$ a_1x_1+a_2x_2+a_3x_3=b $$ — при фиксированных вещественных коэффициентах $ a_1,a_2,a_3 $ (хотя бы один из них считаем отличным от нуля) и $ b_ $ — задает плоскость. Если, к примеру, $ a_1ne 0 $, то из уравнения получаем выражение для $ x_ $ как функции $ x_2,x_3 $: $$ x_1=frac-fracx_2-fracx_3 . $$ В этом представлении переменные $ x_ $ и $ x_ $ могут принимать любые вещественные значения независимо друг от друга, а вот переменная $ x_ $ полностью определяется заданием $ x_ $ и $ x_ $. С одной стороны, последняя формула определяет общее решения системы линейных уравнений (которая в нашем частном случае состоит из одного-единственного уравнения); переменные $ x_ $ и $ x_ $ выбраны основными, а $ x_ $ оказывается зависимой. Строго говоря, координаты любой точки плоскости можно представить формулами $$x_1=frac-fract-fracu, x_2=t, x_3=u quad npu quad subset mathbb R , $$ которые называются параметрическим представлением плоскости. Таким образом, получили геометрическую интерпретацию общего решения системы уравнений. Идем далее: представим последние формулы в векторной форме: $$ left( begin x_1 \ x_2 \ x_3 end right)= left( begin b/a_1- t, a_2/a_1- u, a_3/a_1 \ t \ u end right)= left( begin b/a_1\ 0 \ 0 end right)+ t left( begin -a_2/a_1\ 1 \ 0 end right) + u left( begin -a_3/a_1\ 0 \ 1 end right) . $$ Какой геометрический смысл имеет каждое из слагаемых? Первое слагаемое $$ X_0=left( begin b/a_1\ 0 \ 0 end right) $$ получается при задании $ t=0,u=0_ $ в общем решении. Это — частное решение нашего уравнения и определяет точку, через которую проходит плоскость. Два оставшихся столбца $$ X_1=left( begin -a_2/a_1\ 1 \ 0 end right) quad u quad X_2=left( begin -a_3/a_1\ 0 \ 1 end right) $$ не задают решения нашего уравнения — если только $ bne 0_ $. Но оба удовлетворяют однородному уравнению $$ a_1x_1+a_2x_2+a_3x_3=0 , $$ Последнее также определяет плоскость — параллельную исходной и проходящую через начало координат. Первая плоскость получается из второй сдвигом (параллельным переносом) на вектор $ vec $: и этот факт составляет геометрическую интерпретацию теоремы, сформулированной в конце ☞ ПУНКТА:
Теорема. Общее решение системы уравнений $ A X=mathcal B $ представимо в виде суммы какого-то частного решения этой системы и общего решения соответствующей однородной системы $ A X=mathbb O $.
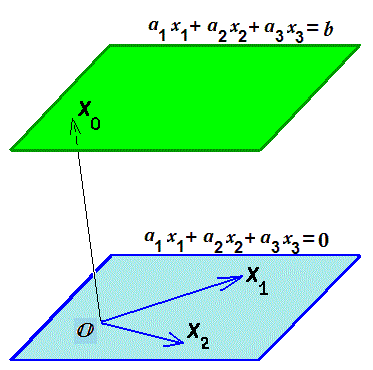
Теперь рассмотрим систему из двух уравнений: $$ left<begin a_x_1 +a_x_2+a_x_3 &=&b_1,\ a_x_1 +a_x_2+a_x_3 &=&b_2. endright. $$ Ее можно интерпретировать как пересечение двух плоскостей в $ mathbb R^ $. Здесь уже возможны варианты: пересечение может оказаться как пустым так и непустым. От чего это зависит? — В соответствии с теоремой Кронекера-Капелли, надо сравнить два числа $$ operatorname left( begin a_ & a_ & a_ \ a_ & a_ & a_ end right) quad u quad operatorname left( begin a_ & a_ & a_ & b_1 \ a_ & a_ & a_ & b_2 end right) . $$ Очевидно, ни одно из них не может быть большим $ 2_ $. Если оба равны $ 2_ $ и этот факт обеспечен, например, условием $$ left| begin a_ & a_ \ a_ & a_ end right| ne 0, $$ то решения системы определяют прямую в пространстве. Действительно, при таком условии систему можно разрешить относительно неизвестных $ x_ $ и $ x_ $ и представить общее решение в виде: $$ x_1= frac<left|begin b_1 & a_ \ b_2 & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>+ frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>x_3 , quad x_2= frac<left|begin a_ & b_ \ a_ & b_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>- frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>x_3 . $$ В этих формулах переменная $ x_ $ принимает любое значение, а значения переменных $ x_ $ и $ x_ $ линейно выражаются через $ x_ $. Общее решение фактически задает прямую в параметрическом виде: координаты произвольной ее точки определяются формулами $$ left( begin x_1 \ x_2 \ x_3 end right)=X_0+tX_1 , $$ где вектор $$ quad X_0 = left(frac<left|begin a_ & b_ \ a_ & b_ end right|><left|begin a_ & a_ \ a_ & a_ end right|> , frac<left|begin a_ & b_ \ a_ & b_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>, 0right)^ $$ задает координаты точки, лежащей на прямой (т.е. принадлежащей пересечению плоскостей), а вектор $$ X_1= left(frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>, — frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>, 1 right)^ $$ является направляющим для прямой. С тем же успехом мы могли бы взять в качестве направляющего вектор, получающийся растяжением $ X_ $: $$ tilde X_1 = left(left|begin a_ & a_ \ a_ & a_ end right|, — left|begin a_ & a_ \ a_ & a_ end right|, left|begin a_ & a_ \ a_ & a_ end right| right)^ . $$ 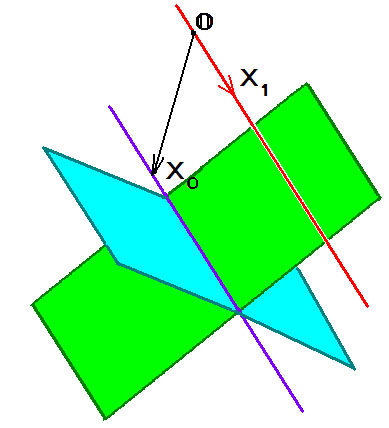
Мы рассмотрели пока только случай пересекающихся плоскостей в пространстве. Его можно считать общим, т.е. случаем «как правило»: две случайным образом выбранные плоскости в $ mathbb R^ $ пересекаться будут. Исследуем теперь исключительный случай — параллельности плоскостей. Исключительность этого случая может быть проверена и аналитикой. Для несовместности системы из двух уравнений необходимо, чтобы ранг ее матрицы $$ left( begin a_ & a_ & a_ \ a_ & a_ & a_ end right) $$ оказался меньшим $ 2_ $. Это равносильно тому, что все миноры второго порядка этой матрицы обращаются в нуль: $$ left| begin a_ & a_ \ a_ & a_ end right|=0, left| begin a_ & a_ \ a_ & a_ end right| =0, left| begin a_ & a_ \ a_ & a_ end right|=0 . $$ Эти условия можно переписать в виде $$ frac<a_><a_>=frac<a_><a_>=frac<a_><a_> ; $$ и, если обозначить общую величину последний отношений через $ tau_ $, то получаем: $$ (a_,a_,a_)=tau (a_,a_,a_) . $$ Если вспомнить, что каждый из этих наборов коэффициентов задает вектор $ vec<OA^> $ в $ mathbb R^ $, перпендикулярный соответствующей плоскости, то, в самом деле, плоскости, определяемые уравнениями, оказываются параллельными. Пересекаться они, как правило, не будут: для пересечения необходимо, чтобы расширенная матрица системы $$ left( begin a_ & a_ & a_ & b_1 \ a_ & a_ & a_ & b_2 end right) $$ имела ранг меньший $ 2_ $. Это возможно только при условии когда коэффициенты правых частей удовлетворяют соотношению $$ b_1 = tau b_2 $$ при величине $ tau_ $ определенной выше. При выполнении этого условия второе уравнение получается из первого домножением на $ tau_ $ и соответствующие плоскости попросту совпадают.
Перейдем теперь к системе из трех уравнений: $$ left< begin a_x_1 +&a_x_2+&a_x_3=&b_1, \ a_x_1 +&a_x_2+&a_x_3=&b_2, \ a_x_1 +&a_x_2+&a_x_3=&b_3. end right. $$ Вариантов взаимного расположения трех плоскостей в $ mathbb R^ $ уже значительно больше. Какой из них будет самым распространенным, то есть случаем «как правило»? Геометрически ответ очевиден: если пересечение двух плоскостей определяет, как правило, прямую, то эта прямая пересекается с третьей плоскостью, как правило, в одной-единственной точке. И алгебра подтверждает геометрию: в комментарии к теореме Крамера говорится, что система, число уравнений которой совпадает с числом неизвестных, как правило, имеет единственное решение. Условие для этого случая «как правило» дается той же теоремой Крамера: $$ left| begin a_ & a_ & a_\ a_ & a_ & a_ \ a_ & a_ & a_ end right| ne 0 . $$
Теорема Кронекера-Капелли в этом случае не нужна — нет, она остается справедливой! — но проверка условия на ранги матриц тривиальна: они оба равны $ 3_ $. Если же указанный определитель обращается в нуль, то этот факт эквивалентен тому, что три строки определителя линейно зависимы. Например, возможно, что строка $ (a_,a_, a_) $ может быть представлена в виде линейной комбинации первых двух строк. Вспомним геометрический смысл этих строк: они задают координаты векторов, перпендикулярных соответствующим плоскостям. Если система уравнений $$ left<begin a_x_1 +a_x_2+a_x_3 &=&b_1,\ a_x_1 +a_x_2+a_x_3 &=&b_2 endright. $$ определяет прямую в $ mathbb R^ $, то оба вектора $ vec<OA^> $ и $ vec<OA^> $ при $ A^= (a_,a_, a_) $ и $ A^= (a_,a_, a_) $ перпендикулярны этой прямой; любая их комбинация также перпендикулярна этой прямой, а, следовательно, плоскость $$ a_x_1 +a_x_2+a_x_3 =b_3 $$ будет ей параллельна.
Статья не закончена!
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Ортогональность
Геометрические соображения из предыдущего пункта могут быть обобщены на случай когда размерности рассматриваемых пространств увеличиваются, и мы говорим о точках и векторах многомерных пространств. В последующих пунктах нам потребуются понятия линейной оболочки, линейного пространства, размерности, базиса и координат применительно к векторам-столбцам или векторам-строкам. Их можно найти ☞ ЗДЕСЬ.
Задача решения системы линейных уравнений $$ left< begin 3x_1&+4x_2&-x_3&=2, \ x_1&-2x_2&+3x_3&=1 end right. $$ может быть рассмотрена с двух точек зрения. С одной стороны, переписав систему в виде $$ x_1left(begin 3 \ 1 end right)+ x_2left(begin 4 \ -2 end right)+ x_3left(begin -1 \ 3 end right)= left(begin 2 \ 1 end right) , $$ можно говорить о поиске линейной комбинации столбцов $$ left(begin 3 \ 1 end right), left(begin 4 \ -2 end right), left(begin -1 \ 3 end right) $$ равной заданному столбцу $$ left(begin 2 \ 1 end right) . $$ В случае произвольной системы, записанной в матричном виде $$ A_X=mathcal B_ $$ совместность системы интерпретировать в смысле принадлежности столбца $ mathcal B $ линейной оболочке столбцов $ A_,dots,A_ $: $$ mathcal B=x_1 A_+dots+x_nA_ quad iff quad mathcal B in mathcal L (A_,dots,A_) . $$ В случае положительного ответа числа $ x_,dots,x_n $ интерпретируются как координаты столбца $ mathcal B $ в системе столбцов 11) $ <A_,dots,A_> $.
С другой стороны, к той же задаче решения системы уравнений, в предыдущем ПУНКТЕ мы подошли с другой стороны. Первое из уравнений системы $$ 3,x_1+4,x_2-x_3=2 $$ можно интерпретировать так: скалярное произведение векторов $ vec<^> $ и $ vec<> $ равно фиксированному числу $ 2_ $. Здесь вектора рассматриваются в пространстве строк $ mathbb R_^ $; считается, что каждый вектор имеет начало в начале координат $ mathbf O=[0,0,0] $, а конец — в точке с координатами $ [3,4,-1] $ или, соответственно, $ [x_1,x_2,x_3] $. Если скалярное произведение векторов обозначать скобками $ langle mbox rangle $, то систему уравнений можно переписать в виде $$ langle vec<^> , vec<> rangle=2, langle vec<^> , vec<> rangle=1 quad npu quad A^ = [3,4,-1], A^=[1,-2,3] $$ — строках матрицы $ A_ $. И задачу решения такой системы понимать в смысле: найти координаты всех векторов-строк $ [x_1,x_2,x_3] $ которые обеспечат нам заданные значения скалярных произведений с двумя фиксированными векторами.
Геометрическая интерпретация еще более упрощается если рассмотреть случай однородной системы уравнений. Так, решить систему уравнений $$ left< begin 3x_1&+4x_2&-x_3&=0, \ x_1&-2x_2&+3x_3&=0 end right. $$ означает подобрать вектор $ vec<> $ перпендикулярный (ортогональный) одновременно обоим векторам $ vec<^> $ и $ vec<^> $. Очевидно, что таких векторов в $ mathbb R^ $ бесконечно много — найдя хотя бы один такой вектор $ vec<> $, другие получим его растяжением: $ alpha cdot vec<> $ остается перпендикулярным векторам $ vec<^> $ и $ vec<^> $ при $ forall alpha in mathbb R $.
Все эти геометрические соображения обобщаются в произвольное пространство $ mathbb R_^ $ строк или столбцов, состоящих из $ n_ $ вещественных чисел (компонент). Для этого приходится обобщать понятие скалярного произведения. В общем случае оно вводится аксиоматически (и, более того, в одном и том же множестве может быть определено разными способами, см. ☞ ЕВКЛИДОВО ПРОСТРАНСТВО ). Мы сейчас не будем залезать так глубоко в эту аксиоматику, а просто определим скалярное произведение двух строк $ X=[x_1,x_2,dots,x_n] $ и $ Y=[y_1,y_2,dots,y_n] $ формулой $$ langle X,Y rangle=x_1y_1+x_2y_2+dots+x_ny_n $$ и продекларируем без обоснований, что все привычные нам по случаям $ mathbb R^ $ и $ mathbb R^ $ свойства скалярного произведения будут выполнены.
В терминах скалярного произведения, задачу решения системы линейных уравнений можно переформулировать как поиск строки $ X=[x_1,x_2,dots,x_n] $, ортогональной всем строкам матрицы $ A_ $: $$ langle A^,X rangle=0, langle A^,X rangle=0,dots, langle A^,X rangle=0 . $$ Множество таких строк образует линейное подпространство пространства $ mathbb R_^ $, это подпространство является ортогональным дополнением линейной оболочки $ mathcal L ( A^, A^,dots, A^ ) $ в пространстве $ mathbb R_^ $. Это подпространство называется нуль-пространством матрицы или ядром матрицы $ A_ $ и обозначается 12) $ er (A) $. Фундаментальная система решений системы $ AX=mathbb O $ составляет базис этого подпространства. Для произвольного линейного пространства количество векторов его базиса называется размерностью пространства и обозначается $ operatorname $. Во введенных обозначениях теорема из ☞ ПУНКТА переформулируется так:
Теорема. $ operatorname left( er (A) right)=n- mathfrak r $, где $ n_ $ — количество столбцов матрицы $ A_ $, а $ mathfrak r=operatorname (A) $ — ее ранг.
Видео:Способы решения систем нелинейных уравнений. 9 класс.Скачать

Системы алгебраических уравнений в математике с примерами решения и образцами выполнения
Целые рациональные функции от нескольких переменных: В этой главе мы изучим системы уравнений от нескольких переменных. В основном мы будем рассматривать системы алгебраических уравнений, то есть уравнений, обе части которых являются целыми рациональными функциями от неизвестных. Понятие целой рациональной функции от нескольких переменных определяется точно так же, как и в случае одного переменного; исходным, как и тогда, будет служить понятие целого рационального выражения.
Алгебраическое выражение, получающееся из чисел и букв x, у, … , z с помощью операций сложения и умножения, называется целым рациональным выражением от х, у, …, z. Примерами целых рациональных выражений являются:
Как и в случае выражений от одного переменного, каждое целое рациональное выражение от нескольких переменных можно привести к каноническому виду. Речь идет о суммах одночленов, то есть о выражениях вида 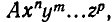
Правила действия над многочленами вытекают из основных законов алгебры.
Видео:7 класс, 37 урок, Системы двух линейных уравнения с двумя переменными. Основные понятияСкачать

Системы уравнений
Рассмотрим некоторые общие вопросы теории систем уравнений. Для простоты ограничимся системами уравнений с двумя неизвестными, хотя основные результаты применимы и к системам уравнений с большим числом неизвестных.
Рассмотрим систему уравнений
Она выражает следующую задачу: найти все пары чисел (а, b) такие, что
Пары чисел (а, b), обладающие этим свойством, называют решениями системы (1). Если множество решений системы пусто, то система называется несовместной.
Тот факт, что пара (а, Ь) является решением системы уравнений с неизвестными х и у, записывается обычно в виде:
Например, пара чисел 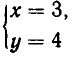
Помимо решения 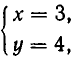
Позже мы увидим, что иных решений она не имеет.
Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными
Возьмем любое уравнение относительно х и у:
и рассмотрим все точки М (х, у) некоторой плоскости, координаты которых удовлетворяют этому уравнению. Эти точки образуют не которое множество Г, и мы будем говорить, что уравнение (1) задает (или выражает) это множество. Обычно множество Г является некоторой линией. В этом случае уравнение (1) называют уравнением линии Г.
Чтобы найти точки линии 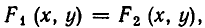
Может случиться, что это уравнение не имеет ни одного действительного корня. Тогда на линии нет точек с абсциссой х = а. Если же уравнение (2) имеет один или несколько корней, то каждому корню соответствует точка линии, имеющая абсциссу а.
Для некоторых уравнений на плоскости нет ни одной точки, координаты которых удовлетворяли бы этим уравнениям. Примером может служить
Ведь если х и у — действительные числа, то 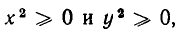
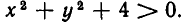
Так как 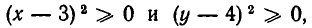
Однако такие случаи являются в некотором смысле исключи тельными, и мы ограничимся рассмотрением случаев, когда уравнение 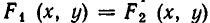
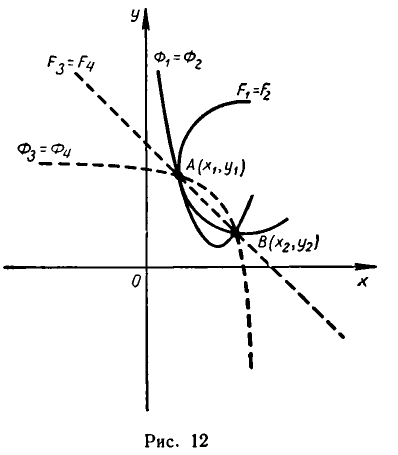
Перейдем теперь к выяснению геометрического смысла решений систем уравнений с двумя неизвестными. Возьмем такую систему:
Каждому из этих уравнений соответствует линия, координаты всех точек которой (и только этих точек!) удовлетворяют этому уравнению. Мы же ищем точки М (.х, у), координаты которых удовлетворяют обоим уравнениям. Ясно, что эти точки принадлежат обеим линиям, то есть являются точками их пересечения.
Итак, задача о решении системы уравнений равносильна зада че об отыскании точек пересечения соответствующих линий. Каждой точке пересечения линий соответствует решение системы.
Совокупность уравнений
образуют совокупность, если требуется найти все пары чисел х = а, у = b, удовлетворяющие хотя бы одному из уравнений (1). Все такие пары чисел (а, Ь) будем называть решениями совокупности (1). Геометрически решения совокупности (1) изображаются фигурой, образованной объединением всех кривых
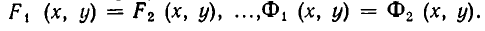
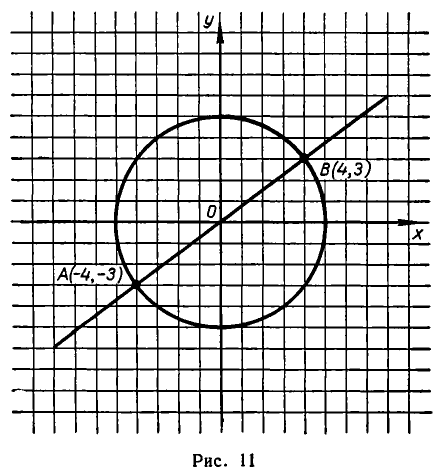
Например, возьмем уравнения 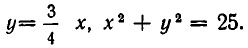
то решения будут изображаться точками пересечения прямой и окружности (то есть точками Л и В на рис. 11). Если же рассматривать эти уравнения как совокупность уравнений
то решение этой совокупности изображаются геометрической фигурой, получаемой объединением прямой и окружности.
Чтобы различать системы уравнений и совокупности уравнений, мы и стали обозначать систему уравнений так:
а совокупность уравнений так:
Можно говорить и о таком более сложном понятии, как совокупность систем уравнений. Например, возьмем такую запись:
Она означает, что надо найти решения системы уравнений
и найти решения системы уравнений
и объединить найденные решения.
Геометрически это изображается так: надо найти точки пересечения линий 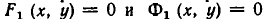
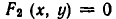
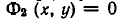
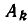
Равносильные системы уравнений
Две системы уравнений
называются равносильными, если всякое решение первой системы является решением второй, а всякое решение второй системы является решением первой.
В частности, любые две несовместные системы уравнений равносильны.
Геометрически это означает следующее: линии 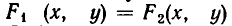
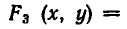
Процесс решения системы уравнений заключается в том, что ее последовательно заменяют равносильными ей системами уравнений (или совокупностями систем уравнений) до тех пор, пока не придут к совокупности вида:
Эта совокупность и дает решения заданной системы уравнений.
При решении систем уравнений чаще всего используются следующие теоремы о равносильности.
Теорема:
заменить любое из уравнений равносильным ему уравнением, то получим систему, равносильную первоначальной.
Доказательство:
Пусть 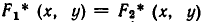
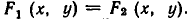
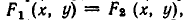
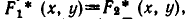
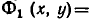
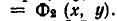
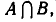
является пересечение 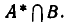
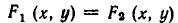
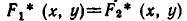
а значит, и 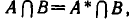
Из этой теоремы вытекает такое
Следствие:
Каждая система уравнений
равносильна некоторой системе уравнений вида
В самом деле, уравнение 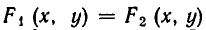
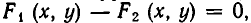
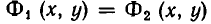
Теорема:
Если функции 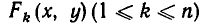
равносильно совокупности уравнений
Доказательство:
Если 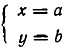
Но произведение нескольких чисел может равняться нулю тогда и только тогда, когда равен нулю хотя бы один из сомножителей. Поэтому для некоторого 
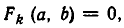
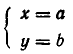
Обратно, если 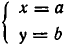
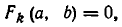
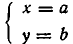
Из теоремы 2 вытекает.
Следствие:
равносильна совокупности систем уравнений
Например, система уравнений
равносильна совокупности систем
Это следствие позволяет сводить системы к совокупностям более простых систем
Метод подстановки
Теоремы п. 5 относятся по сути дела к отдельным уравнениям, а не к системе в целом. При решении систем уравнений применяются также преобразования уравнений, затрагивающие не одно уравнение, а несколько. Например, для решения системы
мы находим из первого уравнения выражение у через 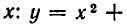
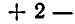
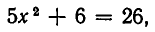
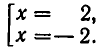
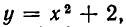
Метод, которым была решена эта система, называется методом подстановки. Он позволяет сводить решение системы уравнений с двумя неизвестными к более простой задаче — решению одного уравнения с одним неизвестным. Выясним теперь, на чем же основан метод подстановки. Для этого докажем следующую теорему.
Теорема:
равносильна системе уравнений
Доказательство:
Пусть 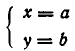
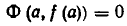
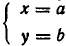
Обратно, пусть 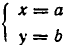
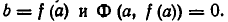
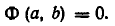
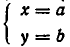
Тем самым равносильность систем уравнений (1) и (2) доказана.
Из теорем 2 и 3 вытекает
Следствие:
Если уравнение F (х, у)=0 равносильно уравнению 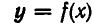
равносильна системе уравнений
Мы уже говорили, что теорема 3 лежит в основе метода решения систем уравнений с двумя неизвестными, называемого методом исключения неизвестных. Он состоит в следующем.
Пусть задана система уравнений
Выразим из первого уравнения системы у через х, то есть заменим уравнение F(х, у)= 0 равносильным ему уравнением у = f(х). Полученное выражение для у подставим во второе уравнение, то есть заменим систему уравнений (1) равносильной ей системой
Уравнение Ф (х,f(x)) является уже уравнением с одним неизвестным. Решая его, получим корни 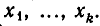

Часто приходится заменять уравнение F(х,у)= 0 не одним уравнением вида у = f(х), а совокупностью
таких уравнений. Тогда и система (1) заменяется совокупностью систем
Из каждой системы этой совокупности получаем описанным выше методом решения заданной системы, после чего объединяем их.
Примеры:
- Решить систему уравнений:
Из первого уравнения системы находим 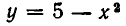
или, после упрощения,
Корнями этого биквадратного уравнения являются числа:
Им соответствуют значения:
Значит, решения заданной системы уравнений имеют вид:
2. Решить систему уравнений:
Из первого уравнения системы получаем:
Значит, нам надо решить совокупность двух систем уравнений:
Делая в первой системе подстановку, получаем:
или 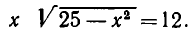
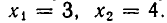
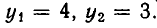
Точно так же доказывается, что вторая система имеет решения:
Следовательно, заданная система имеет решения:
Метод алгебраического сложения уравнений
Кроме метода подстановки, при решении систем алгебраических уравнений применяется метод алгебраического сложения. Он основан на следующей теореме.
Теорема:
Если к одному из уравнений системы
прибавить другое уравнение, умноженное на любой множитель f(x, y), определенный при всех допустимых значениях неизвестных, а второе уравнение оставим неизменным, то получится система уравнений, равносильная исходной.
Таким образом, система (1) равносильна системе
где множитель f(х,у) определен при всех допустимых значениях неизвестных.
Доказательство:
Пусть х = а, у = b — решение системы (1), то есть F(а, b)=0 и Ф(а, b)= 0.
Умножим обе части равенства Ф(а, b)=0 на число f(а, b) и прибавим к равенству F (а, b)= 0. Мы получим, что F(а, b)+(а, b) Ф(а,b)= 0, а потому х =а, у = b удовлетворяет и системе (2).
Точно так же доказывается, что любое решение системы уравнений (2) удовлетворяет системе уравнений (1). Значит, системы уравнений (1) и (2) равносильны.
Из теоремы 4 вытекает такое
Следствие:
Если к одному из уравнений системы (1) прибавить другое уравнение системы, умноженное на любое число, а второе уравнение оставить неизменным, то получим систему, равносильную первоначальной.
Покажем, как применяются эти утверждения для решения систем уравнений. Пусть дана система уравнений:
Здесь нецелесообразно выражать х через у или у через х, так как мы получили бы довольно сложное иррациональное уравнение. Поэтому поступим иначе. Прибавим к первому уравнению системы второе уравнение, умноженное на 3. В силу формулы для куба суммы получим систему уравнений:
равносильную заданной. Эта система равносильна системе:
(поскольку уравнение 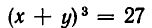
А теперь выразим из первого уравнения у через х и подставим во второе уравнение. Мы получим:
Из второго уравнения находим: 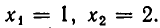
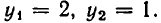
Задача:
Массы трех планет 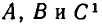
система координат. Координаты планет равны соответственно A(0,0), В (а, 0), С (2а, b). При каком значении b на плоскости существует точка, в которой притяжение ко всем трем планетам одинаково?
Решение:
По закону всемирного тяготения сила притяжения между телами с массами 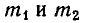
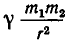
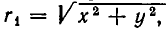
а до точки С (b, с) равно
Поэтому силы, с которыми тело массы m, находящееся в точке D, притягивается к планетам, равны
По условию задачи должны выполняться условия 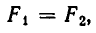
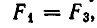
После сокращения обоих уравнений на 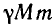
Вычтем первое уравнение из второго. Мы получим, что
Подставляя это значение у в первое уравнение, получаем для х квадратное уравнение
Из него находим:
Отсюда получаем, что х принимает действительные значения лишь в случае, когда 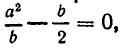
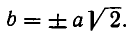
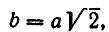
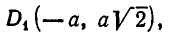
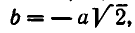
Метод введения новых неизвестных
Для решения многих систем оказывается удобно ввести вместо х и у новые неизвестные. Рассмотрим следующий пример:
Если положить 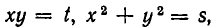
Решая эту систему, получаем, что
Так как 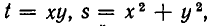
Решениями первой системы являются:
Вторая же система не имеет действительных решений.
Общего правила для выбора новых неизвестных не существует. Однако в некоторых случаях можно указать полезные правила.
Системы однородных уравнений
Назовем f (х, у) однородным многочленом относительно х и у степени n, если при замене х на ах и у на ау F (х, у) умножается на
Например, 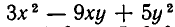
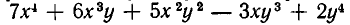
Пусть одно из уравнений системы имеет вид: F (х,у) = 0, где F (х, у)— однородный многочлен. Тогда решение системы сводится к решению двух уравнений, каждое из которых содержит лишь одно неизвестное. Покажем на примере, как это делается.
Пусть дана система уравнений:
Посмотрим сначала, есть ли у этого уравнения решения, для которых х =0. Подставляя х = 0 в оба уравнения системы, получаем систему уравнений:
Эта система несовместна, так как из первого уравнения получаем у = 0, а из второго —
Итак, система не имеет решений, для которых х = 0. Поэтому первое уравнение системы можно разделить на 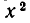
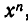
Положим у — tх. Мы придем к системе уравнений:
Корнями первого уравнения являются 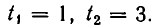
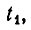
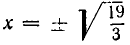
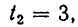
В следующем примере система имеет решения, для которых х = 0:
При х = 0 первое уравнение обращается в равенство 0=0, а второе принимает вид 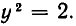
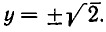
Другие решения получаются так же, как и в первом случае. Мы делим первое уравнение системы на 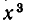
Из первого уравнения находим 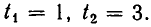
Задача:
От пристани А одновременно отправились вниз по течению катер и плот. Катер спустился вниз по течению на 96 км, затем повернул обратно и вернулся в А через 14 часов. Найти скорость катера в стоячей воде, если известно, что катер встретил плот на обратном пути на расстоянии 24 км от А.
Решение:
Сначала составим систему уравнений. В качестве неизвестных выберем скорость u катера в стоячей воде и скорость течения v. Тогда скорость катера при движении по течению равна u+v, а при движении против течения u-v. Значит, чтобы пройти вниз по течению 96 км, ему надо 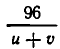
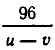
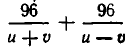
Чтобы получить второе уравнение, найдем, какое время затратил катер до встречи с плотом. Он прошел 96 км вниз по течению и 72 км против течения. На это он затратил 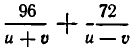
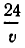
Мы получим систему уравнений:
При замене u на ut и v на vt обе части второго уравнения умножаются на 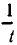
Освобождаясь от знаменателей, получим:
Так как 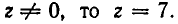
откуда v = 2 (км/ч). Поэтому u = 14 км/ч.
Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными
Мы уже знаем, что решение системы двух уравнений с двумя неизвестными
геометрически истолковывается как отыскание точек пересечения двух линий. Этим можно воспользоваться для приближенного решения системы уравнений. Именно, если изобразить линии F(х, у) = 0 и Ф(х, у) = 0, мы сможем найти координаты точек пересечения этих линий и тем самым значения неизвестных. Поскольку линии чертятся лишь приближенно, мы получаем не точные, а приближенные значения решений системы. Тем не менее, решая графически систему, мы можем узнать, сколько она имеет решений, и, хотя бы грубо, найти приближенные значения этих решений.
При графическом решении систем уравнений мы сталкиваемся с различными кривыми. В курсе геометрии были выведены уравнения прямой, окружности, параболы, гиперболы и эллипса. В дальнейшем мы будем пользоваться этими кривыми.
Рассмотрим некоторые примеры систем уравнений.
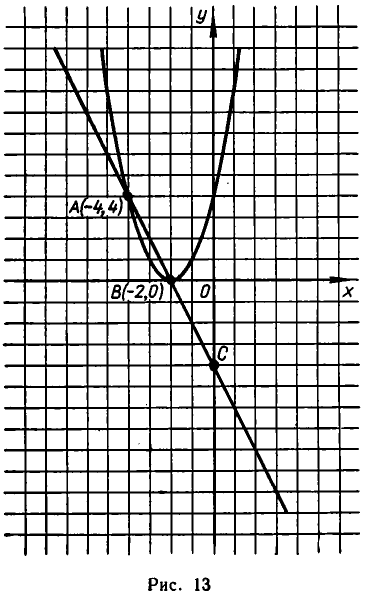
Пусть дана система
Выразив из уравнения (2) у через х и подставив в первое уравнение, получаем квадратное уравнение:
Подставив их во второе уравнение, получаем:
Итак, система имеет два решения:
Построим теперь линии, выражаемые уравнениями (1) и (2). Уравнение (1) — это уравнение параболы 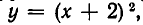
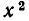
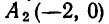
Парабола может иметь с прямой линией не две, а одну точку пересечения и даже не иметь ни одной точки пересечения.
Возьмем систему уравнений:
Ее единственное решение:
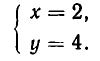
Из рис. 14 мы видим, что прямая у = 2х касается параболы
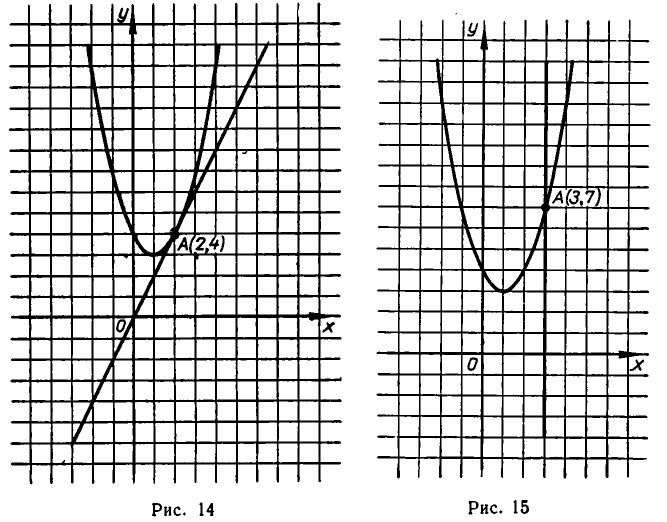
тоже имеет одно решение:
Но в этом случае прямая не касается параболы, а пересекает ее (см. рис. 15).
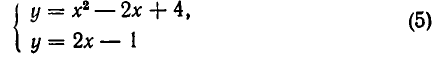
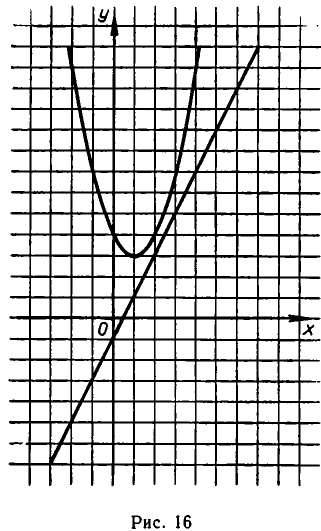
не имеет ни одного решения — здесь прямая и парабола не пересекаются (см. рис. 16).
Теперь рассмотрим систему, геометрический смысл которой заключается в отыскании точек пересечения прямой и гиперболы. Пусть система имеет вид:
Решая ее способом подстановки, находим решения:
Эти же решения получаются графическим способом (см. рис. 17). Однако следует иметь в виду, что графический способ дает лишь приближенные значения корней и, решая систему (6) графически, мы не можем быть уверены, что решение имеет вид х = —4, у = —3, а не, например, х = —4,01, у = —2,99.
Как и в случае параболы, может случиться, что прямая имеет не две, а меньше общих точек с гиперболой.
Перейдем к системам, в которых оба уравнения имеют вторую степень. Можно доказать, что такие системы уравнений имеют не более четырех решений.
Вообще можно доказать, что система двух уравнений с двумя неизвестными такая, что первое уравнение имеет степень m, а второе — степень n, имеет не более mn решений.
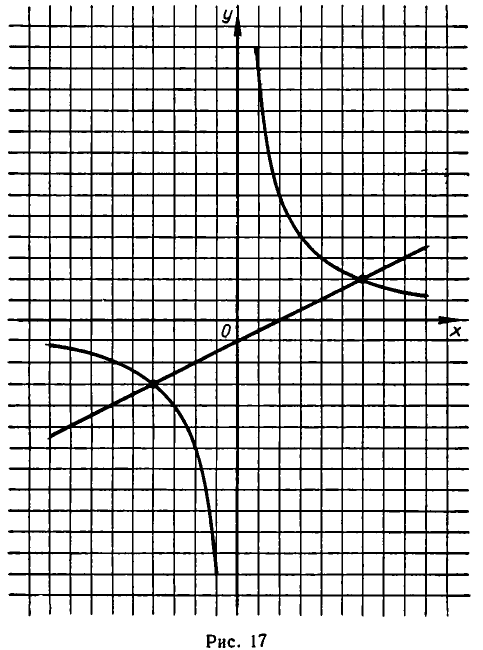
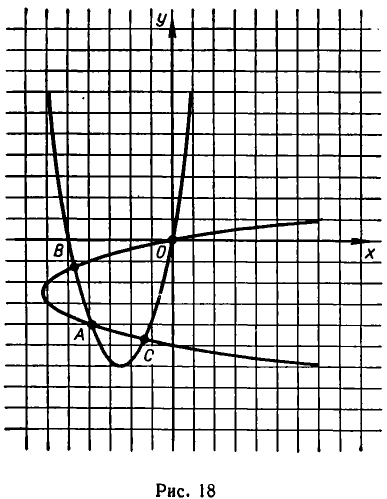
Рассмотрим, например, систему:
Первое из этих уравнений представляет параболу с осью, параллельной оси ординат, а второе — параболу с осью, параллельной оси абсцисс (см. рис. 18). Из рисунка видно, что эти параболы пересекаются в четырех точках. Чтобы найти координаты точек пересечения,
решим эту систему методом алгебраического сложения. Именно, вычтем из уравнения (8) уравнение (7). Мы получим равносильную систему уравнений:
Эта система равносильна совокупности систем:
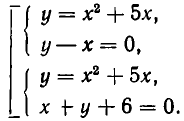
Обе системы этой совокупности решаются методом подстановки. Мы получаем при этом следующие решения заданной системы:
тоже имеет четыре решения. Она выражает задачу об отыскании точек пересечения окружности и гиперболы (см. рис. 19). Что бы решить эту систему, надо прибавить к первому уравнению удвоенное второе уравнение.
В некоторых случаях получается меньше чем четыре решения системы. Например, система
имеет два решения. Она выражает задачу об отыскании точек пересечения параболы и окружности (рис. 20).
Столько же решений имеет система
(пересечение двух окружностей) (рис. 21).
Видео:6 класс, 30 урок, Системы линейных уравнений с двумя переменнымиСкачать

Решение других типов систем алгебраических систем уравнений
Пример:
Решить систему уравнений
Решение:
Из данной системы можно исключить 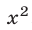
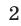
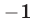
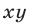
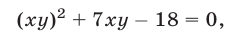
откуда 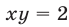
Система (1), (2), равносильная системе (1), (3), распадается на две системы:
Из первой системы находим
Из второй системы получаем
Ответ. 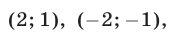
Пример:
Решить систему уравнений
Решение:
Если 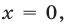
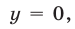
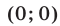
Пусть 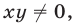
где 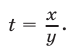
имеет корни
Заметим, что при 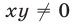
Если 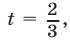
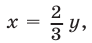
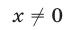
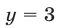
Если 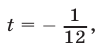
Ответ.
Пример:
Решить систему уравнений
Решение:
Допустимые значения 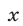
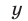
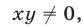
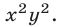
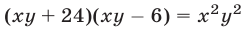
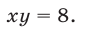
Так как обе части уравнений (7) и (8) отличны от нуля, то система (9), (7) равносильна системе (7), (8). Исключая у из системы (9), (7), получаем
Из (10) следует, что 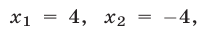
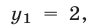
Ответ.
Пример:
Решить систему уравнений
Решение:
Запишем первое уравнение в виде
Решив это уравнение как квадратное относительно 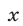
Таким образом, исходная система распадается на следующие две системы:
Пример:
Решить систему уравнений
Решение:
Исключив 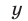
нахождение корней которого — совсем не простая задача. Более эффективный способ основан на разложении левой части уравнения (12) на множители:
Отсюда вытекает, что система (11), (12) распадается на следующие две системы:
Первая из этих систем не имеет действительных решений, а вторая имеет два решения.
Ответ.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
Видео:Решение системы неравенств с двумя переменными. 9 класс.Скачать

Решение системы алгебраических уравнений по правилу Крамера и методом обратной матрицы
Пусть дана система линейных уравнений, состоящая из n
линейных уравнений с n неизвестными:
Здесь 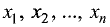
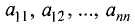
циенты при неизвестных, 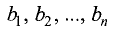
Определитель, состоящий из коэффициентов при неизвестных,
называется определителем системы.
Для рассматриваемого случая определитель системы имеет вид
Предположим, что этот определитель отличен от нуля. Пусть i —
любое число от 1 до n . Умножим обе части первого равенства
системы уравнений (2.1) на алгебраическое дополнение 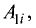
получающееся вычеркиванием первой строки и i-го столбца в определителе системы. Обе части второго равенства этой системы умножим на алгебраическое дополнение 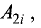
Сложим левые и правые части получившейся системы
уравнений, скомпоновав их следующим образом:
Коэффициентом при 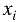
системы D. При всех остальных х коэффициенты будут равны нулю,
так как они являются суммой произведений всех элементов столбцов
определителя на алгебраические дополнения соответствующих
элементов другого столбца (п. 5 свойств определителей, § 1.9). Правая
часть равенства является определителем, полученным из
определителя системы D после замены в нем i-го столбца столбцом из
свободных членов системы уравнений. Обозначим этот определитель 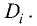
Так как 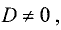
Этот метод решения системы линейных уравнений называется
правилом Крамера.
Правило Крамера. Пусть D — определитель системы п линейных
уравнений, состоящий из коэффициентов при неизвестных, a 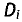
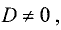
Пример:
Решить систему линейных уравнений:
Решение:
Определитель этой системы отличен от нуля:
После замены в этом определителе соответствующих столбцов
столбцом свободных членов получим
Решение системы уравнений:
Решить систему линейных уравнений можно, используя матричный метод. Для этих целей коэффициенты данной системы, неизвестные и свободные члены представим в виде матриц:
Тогда система линейньк уравнений в матричной форме имеет вид
Умножим слева эту матрицу на
Преобразуем левую часть равенства:
Таким образом, решение в матричной форме можно записать в виде
Пример:
Решить систему линейных уравнений:
Решение:
Определитель данной системы
Обратную матрицу находим по схеме, приведенной в § 1.11:
Находим матрицу решений:
Таким образом, система имеет следующее решение:
Видео:Алгебра 7 класс (Урок№48 - Решение систем двух линейных уравнений с двумя неизвестными.)Скачать

Общий вид системы линейных алгебраических уравнений
Систему из m линейных уравнений с n неизвестными, или систему m х n, можно записать в общем виде следующим образом:
Если так же, как и в предыдущем разделе, ввести обозначения
то система линейных уравнений в матричной форме и ее решение
примут вид
Решение системы линейных алгебраических уравнений методом Гаусса
Метод Гаусса состоит в последовательном исключении переменных. При этом на первом шаге из второго уравнения исключается 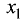
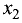
Шаг 1. Предположим, что коэффициент при 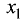
уравнении системы (2.4) 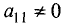
уравнений местами добьемся того, что 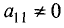
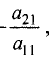
Умножим первое уравнение на 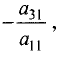
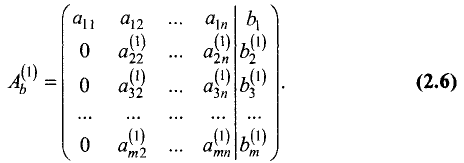
Для удобства записи обычно используют расширенную матрицу системы, отделяя в ней вертикальной чертой столбец свободных членов. После первого шага данная матрица принимает вид:
Шаг 2. Предположим, что коэффициент при 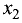
уравнении системы (2.5) 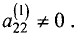
уравнений местами добьемся того, что 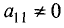
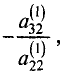
третьим уравнением системы (2.5) или матрицы (2.6) и результат
запишем в виде третьего уравнения системы (2.7) или матрицы
(2.8). Аналогично поступаем с остальными уравнениями системы:
Продолжая процесс последовательного исключения переменных, после (r-1)-го шага получим систему уравнений и расширенную матрицу:
Последние m-r уравнений в системе (2.9) для совместной
системы (2.4) являются тождествами: 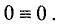
чисел 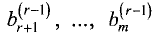
расширенная матрица (2.10) принимают вид
После отбрасывания уравнений, являющихся тождествами,
число оставшихся уравнений может быть либо равно числу
переменных r=n, либо меньше числа переменных. В первом случае
матрица имеет треугольный вид, а во втором — ступенчатый. Переход от системы уравнений (2.4) к равносильной ей системе (2.11)
называется прямым ходом метода Гаусса, а нахождение переменных из системы (2.11) — обратным ходом.
Пример:
Методом Гаусса решить систему уравнений
Решение:
Расширенная матрица этой системы имеет вид
Шаг 1. Расширенную матрицу первого шага получаем за счет
умножения первой строки на —2 и сложения результата со второй
строкой, а также за счет умножения первой строки на -1 и сложения
результата с третьей строкой:
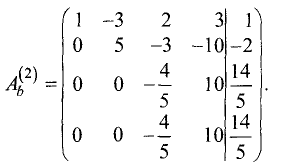
Ш а г 2. Расширенную матрицу первого шага получаем за счет
умножения второй строки на -3 и сложения результата с третьей строкой:
Эта матрица имеет треугольную форму и соответствует системе
линейных уравнений
Отсюда последовательно находим
Пример:
Методом Гаусса решить систему уравнений
Решение:
Расширенная матрица этой системы имеет вид
Ш а г 1. Расширенную матрицу первого шага получаем за счет
умножения первой строки на —2 и сложения результата со второй
строкой, а также за счет умножения первой строки на -4 и сложения результата с третьей строкой:
Ш а г 2. Расширенную матрицу первого шага получаем за счет
умножения второй строки на —1 и сложения результата с третьей строкой:
Уравнение,соответствующее третьей строке последней матрицы, противоречиво. Оно имеет вид 0 = -1. Следовательно, данная система несовместна. ►
Пример:
Методом Гаусса решить систему уравнений
Решение:
Расширенная матрица этой системы имеет вид
Ш а г 1. Первую строку последовательно умножаем на числа -2; —2;
-3 и складываем результат с соответствующими строками исходной
расширенной матрицы:
Ш а г 2. Умножаем вторую строку на 
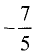
Шаг 3. Умножаем третью строку на -1.
После удаления последнего уравнения приведенная система
уравнений принимает вид
Из этой системы обратным ходом метода Гаусса находим
Так как 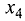
система имеет бесконечное множество решений. ►
Вычисление обратной матрицы методом Гаусса
Этот наиболее простой метод вычисления обратной матрицы
состоит в следующем. Пусть А — невырожденная матрица.
Припишем к ней справа единичную матрицу Е. Далее с помощью
элементарных преобразований над строками расширенной матрицы 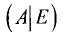
Пример:
Найти матрицу, обратную исходной:
Решение:
Составим расширенную матрицу:
Приведем левую половину этой матрицы к единичной матрице:
Последний столбец левой половины матрицы принял вид
последнего столбца единичной матрицы:
Последний и предпоследний столбцы левой половины матрицы
приняли вид последнего и предпоследнего столбцов единичной матрицы:
Правая половина этой расширенной матрицы является искомой
обратной матрицей, т.е.
Пример:
Найти матрицу, обратную исходной:
Решение:
Составим расширенную матрицу:
Приведем левую половину этой матрицы к единичной матрице:
Правая половина этой расширенной матрицы является искомой
обратной матрицей, т.е.
Видео:Решение систем уравнений. Метод Крамера для системы линейных уравнений с двумя неизвестными.Скачать

Система линейных однородных уравнений
Система m линейных уравнений с n переменными называется системой линейных однородных уравнений, если все ее свободные члены равны нулю.
Такая система имеет вид
Система линейных однородных уравнений всегда совместна, так
как она имеет, по крайней мере, нулевое (тривиальное) решение
Если система (2.13) имеет n линейных уравнений, а ее определитель отличен от нуля, то такая система имеет только нулевое решение. Это следует из правила Крамера. Ненулевое решение возможно для систем линейных однородных уравнений, у которых определитель равен нулю или m Собственные значения и собственные векторы матриц
Пусть матрица имеет порядок n или, что то же самое, размер n х n.
Вектор 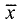
Число 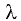
соответствующим вектору 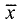
Перенеся правую часть (2.15) в левую и принимая во внимание
соотношение 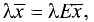
Уравнение (2.16) эквивалентно системе линейных однородных
уравнений
Для существования ненулевого решения системы линейных
однородных уравнений (2.17) необходимо и достаточно, чтобы
определитель коэффициентов этой системы равнялся нулю, т.е.
Этот определитель является многочленом n-й степени относительно
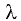
уравнение (2.18) — характеристическим уравнением матрицы А. Корни характеристического уравнения соответствуют собственным числам матрицы А. Определив набор этих чисел, для каждого из них можно найти собственный вектор.
Пример:
Найти собственные числа и собственные векторы
матрицы
Решение:
Характеристическое уравнение этой матрицы имеет вид
Корни характеристического уравнения
Для двух переменных система уравнений (2.17), эквивалентная
уравнению (2.15) собственного вектора, представляется в виде
Подставив сюда значения корней 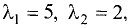
системы уравнений:
Каждая система является одним уравнением, что и следовало
ожидать. Это связано с тем, что определитель системы равен нулю.
Из первой системы для 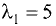
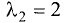
координаты собственных векторов связаны соотношениями
Поскольку 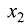
значению матрицы соответствует бесконечное множество собственных векторов различной длины. Положим 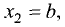
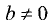
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Системы линейных уравнений с двумя неизвестными
Системой линейных алгебраических уравнений с двумя неизвестными называется система уравнений вида
Числа называются коэффициентами системы; — свободными членами, — неизвестными.
Решением системы называется упорядоченная пара чисел такая, что после замены неизвестных соответственно числами каждое уравнение системы превращается в верное числовое равенство. Система называется совместной, если она имеет хотя бы одно решение. Если система не имеет ни одного решения, то она называется несовместной.
Система (3.26) называется однородной, если все свободные члены равны нулю:
В отличие от однородной, систему общего вида (3.26) называют неоднородной .
Систему (3.26) принято записывать в матричной форме. Для этого из коэффициентов системы составляем матрицу системы
свободные члены записываем в столбец свободных членов , а неизвестные — в столбец неизвестных
Матричная запись неоднородной системы уравнений (3.26) имеет вид
где символ в правой части обозначает нулевой столбец размеров .
Блочная матрица называется расширенной матрицей системы (3.26).
Рассматривается случай, когда все уравнения системы первой степени, т.е. коэффициенты при неизвестных каждого уравнения не равны нулю одновременно. Поэтому матрица системы ненулевая, более того, все ее строки ненулевые.
В соответствии с матричной записью решением системы (3.28) называется столбец , при подстановке которого в (3.28) получаем верное равенство для столбцов в левой и правой частях. В частности, нулевой столбец является решением однородной системы (3.29), т.е. любая однородная система уравнений совместна.
Рангом системы уравнений (3.26) называется ранг матрицы системы: , т.е. максимальное число линейно независимых строк матрицы (максимальное число линейно независимых уравнений системы). Поскольку матрица системы (3.26) ненулевая и содержит два столбца, то ее ранг . Ранг может быть равен либо единице ( , если все строки матрицы пропорциональны), либо двум ( , если имеются две линейно независимые строки).
Выясним геометрический смысл и свойства решений системы уравнений (3.26).
Пусть на плоскости задана аффинная система координат . Как показано ранее, множество точек , координаты которых удовлетворяют линейному уравнению с двумя неизвестными , или , представляет собой прямую. Поэтому множество решений системы уравнений является пересечением прямых .
Видео:7 класс, 40 урок, Системы двух линейных уравнений с двумя переменными как математические моделиСкачать

Примеры пересечения прямых
Если ранг системы (3.26) равен 1, то коэффициенты при неизвестных всех уравнений пропорциональны. В этом случае любые две прямые параллельны (система уравнений несовместна (рис.3.31,а)) или совпадают (в этом случае вся система (3.26) равносильна одному, например, первому ее уравнению (рис.3.31,6)).
Если ранг системы равен 2, то в системе имеются хотя бы два линейно независимых уравнения. Прямые, соответствующие этим уравнениям, пересекаются, например, в точке . Поэтому множество решений системы (3.26) либо одна точка (система совместна, все прямые проходят через точку , т.е. все прямые принадлежат собственному пучку прямых (рис.3.31,в)), либо пусто (система несовместна (рис.3.31,г)).
Для решения системы (3.26) обычно применяется метод Гаусса исключения неизвестных, при котором уравнения системы заменяются линейными комбинациями уравнений, содержащими меньшее количество неизвестных, при этом расширенная матрица системы приводится к ступенчатому виду. Продемонстрируем этот метод на примере.
Пример 3.17. Решить системы уравнений:
Изобразить множество решений на координатной плоскости .
1) Составляем расширенную матрицу системы
Поскольку (элемент — ведущий), прибавим ко второй и к третьей строкам первую, умноженную на и на соответственно:
Последняя строка соответствует уравнению , которое не имеет решений. Следовательно, множество решений системы пустое (прямые, задаваемые уравнениями системы, изображены на рис.3.31,а).
2) Составляем расширенную матрицу системы
Поскольку (элемент — ведущий), прибавим к третьей строке первую, а ко второй — первую, умноженную на
Система равносильна одному уравнению . Множество ее решений представляет собой прямую на координатной плоскости . Координаты любой точки этой прямой удовлетворяют системе уравнений, следовательно, система имеет бесконечно много решений (рис.3.31,6).
3) Составляем расширенную матрицу системы
Поскольку (элемент — ведущий), прибавим ко второй и к третьей строкам первую строку, умноженную на (-1):
Разделим вторую строку на (-6), а затем к первой и третьей строкам прибавим вторую, умноженную на (-2) и на 4 соответственно:
Получили единственное решение , которому соответствует точка на координатной плоскости (рис.3.31,в).
4) Составляем расширенную матрицу системы
Поскольку (элемент — ведущий), прибавим ко второй и к третьей строкам первую строку, умноженную на (-1):
Разделим третью строку на (-4), а затем ко второй строке прибавим третью, умноженную на 6:
Вторая строка соответствует уравнению , которое не имеет решений. Следовательно, система несовместна (прямые, задаваемые уравнениями системы, изображены на рис.3.31,2).
🎦 Видео
ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Нелинейные уравнения. Практическая часть. 9 класс.Скачать

Решение системы линейных уравнений с двумя переменными способом сложения. 6 класс.Скачать

Алгебра 7. Урок 8 - Системы линейных уравненийСкачать