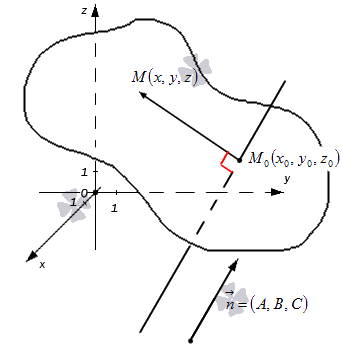
Геометрический смысл коэффициентов при неизвестных в уравнении плоскости (8 видео)

Геометрический смысл коэффициентов при неизвестных в уравнении плоскости

Выяснить геометрический смысл коэффициентов A, B и C в общем уравнении плоскости Ax + By + Cz + D = 0.

1. Рассмотрим вектор с проекциями на координатные оси, соответственно равными A, B и C, т. е. .

2. Возьмем на плоскости Ax + By + Cz + D = 0 две произвольные точки M( x₁, y₁, z₁) и N( x₂, y₂, z₂) и рассмотрим вектор . Этот вектор лежит в плоскости Ax + By + Cz + D = 0. Его проекции на координатные оси соответственно равны x₂ — x₁, y₂ — y₁, z₂ — z₁ и .

3. Так как точки M и N лежат в плоскости Ax + By + Cz + D = 0, то имеют место равенства

Вычитая первое уравнение из второго, получим

Скалярное произведение вектора на вектор равно

Так как на основании (1) это скалярное произведение равно нулю, то вектор перпендикулярен вектору , а тем самым и той плоскости, в которой лежит этот вектор, т. е. вектор перпендикулярен плоскости Ax + By + Cz + D = 0.

Геометрическое значение коэффициентов A, B и C в общем уравнении плоскости Ax + By + Cz + D = 0 состоит в том, что они являются проекциями на координатные оси Ox, Oy, Oz вектора, перпендикулярного этой плоскости.

Содержание

Общее уравнение плоскости : описание, примеры, решение задач
Общее уравнение плоскости: основные сведения
Общее уравнение плоскости, проходящей через точку
Неполное общее уравнение плоскости
Линейная функция
Геометрический смысл коэффициентов
Физический смысл коэффициентов линейного уравнения
Построение графика линейной функции на основе геометрического моделирования операций
📸 Видео

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Общее уравнение плоскости : описание, примеры, решение задач

В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.

Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Общее уравнение плоскости: основные сведения

Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.

Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.

Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.

Теорема состоит из двух частей. Разберем доказательство каждой из них.

Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .

Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:

n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 )

Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.

Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.

В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость.

Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.

Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.

Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.

Раскроем чуть шире смысл теорем.

В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.

Укажем пример как иллюстрацию этих утверждений.

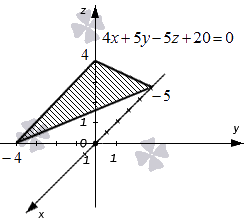
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Общее уравнение плоскости, проходящей через точку

Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.

Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0

Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.

Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:

2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0

Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.

В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.

Решение

Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:

λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.

Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0

Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .

Возможно получить это уравнение другим способом.

Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.

Решение

Рассмотрим два способа решения.

Исходные условия позволяют получить следующие данные:

x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5

Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0

Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:

M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0

Ответ: 3 x + 7 y — 5 z — 26 = 0

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Неполное общее уравнение плоскости

Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

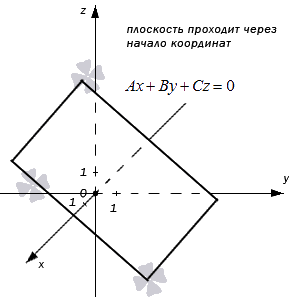
В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0

Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:

A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0

Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.

При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.

Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0

Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.

Решение

Условием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .

Задачу возможно решить еще одним способом.

Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0

Ответ: x — 7 = 0

Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .

Решение

Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .

Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .

Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .

Видео:Видеоурок "Уравнение плоскости в отрезках"Скачать

Линейная функция

Линейной называется функция вида у = ах + 6, где а и b — некоторые числа.

Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

Геометрический смысл коэффициентов

Выясним геометрический смысл коэффициентов а и 6 линейной функции у = ах + 6. Для этого воспользуемся инструментом под названием «Ползунок».

1) Нажимаем клавишу (тем самым берем инструмент) «Ползунок» и кликнем на выбранную точку Полотна. В выпавшем меню компьютер предлагает назвать ползунок, а вместе с ним и параметр, который он изображает, буквой а и установить границы изменения параметра от -5 до 5. Соглашаемся или вводим свои границы. На выбранном месте появляется изображение ползунка .в виде отрезка с точкой. Аналогично строим ползунок для параметра Ь. Изменение каждого из параметров достигается перемещением точки на отрезке. На рисунке 21 установлено: а = 1.6, Ь = 5. 2 3

2) В строку ввода записываем: f(x) = a*x+b. После ввода на Полотне появляется график функции при установленных значениях параметров. В нашем случае это прямая. Отмечаем точки Aw В построенной прямой с осями координат.
3) Строим начало координат О = (0.0), через начало координат проводим прямую параллельно данной прямой, строим точку Е = (1,0), через неё проводим вертикаль и отмечаем точку С пересечения вертикали с прямой, проходящей через начало координат параллельно данной прямой. Угловой коэффициент прямой есть по определению к = у(С). Вводим это число и делаем надпись: «Угловой коэффициент к = у(С) = к». При этом последнее к берем из «Объектов».

Теперь проводим исследование. Видим, что параметр b есть ордината точки В. Это неудивительно, поскольку /(0) = Ь. При изменении параметра а наблюдаем неизменное равенство а = к. Другими словами, коэффициент а равен угловому коэффициенту данной прямой.

Задания. С помощью живого рисунка 21 продемонстрируйте частные случаи линейной функции f(x) = ах + b: 1) а = 1, b = 0; 2) а = 0, b = 1;

3) анимируйте а (Ь) при фиксированном Ь (а).

Видео:Уравнение плоскости. 11 класс.Скачать

Физический смысл коэффициентов линейного уравнения

Выясним физический смысл коэффициентов в уравнении прямой у = кх + Ь.

На живом рисунке 22 точка С равномерно движется от начала координат вверх по оси ординат со скоростью v. (Например, воздушный шар поднимается с земли с постоянной скоростью.) За время х точка С пройдет путь у = vx. Получили линейную функцию вида у = кх. Следовательно, физический смысл углового коэффициента к состоит в том, что он равен скорости равномерного движения у = vx. Если в начальный момент точка С находится не в начале координат, а отстоит от него на расстоянии Ь_у то зависимость пройденного расстояния от времени выразится равенством у = vx + Ь.

Смоделируем движение, задаваемое линейной функцией у = их.

Построение (рис. 22).

1) Строим точки О = (0,0), Е = (1,0), единичную окружность, отмечаем на ней точку А и проводим прямую О А.
2) Проводим вертикаль через точку Е и отмечаем точку D пересечения вертикали с прямой О А.
3) На положительном луче оси абсцисс строим отрезок OF и отмечаем на нём точку X. Проводим через неё вертикаль и отмечаем точку В пересечения вертикали с прямой О А. Через В проводим горизонталь и отмечаем точку С пересечения горизонтали с осью ординат. Делаем эту точку большой, в виде шара.

При анимации точки X точка С демонстрирует равномерное движение по вертикали (шар поднимается вверх). Заметим, что для достижения равномерного движения точки X её нужно взять именно на отрезке оси абсцисс. Чем меньше скорость, тем больше времени требуется для прохождения данного расстояния. Следовательно, при малой скорости (при малом угле наклона прямой) отрезок AF_y по которому перемещается точка X, нужно удлинять, а при большой скорости (при большом угле наклона прямой О А) — укорачивать.

На рисунке 22 видим, что угловой коэффициент к = tga = 7777- Сле-

довательно, к есть отношение пройденного пути к единице измерения времени. Таким образом, к есть скорость равномерного движения. Изменяя положение точки А на окружности, наблюдаем изменение скорости движения шара С.

Задание. Смоделируйте равномерное движение точки оси абсцисс по закону у = vx + Ь.

Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

Построение графика линейной функции на основе геометрического моделирования операций

Создадим в среде GeoGebra виртуальный прибор для вычерчивания графика линейной функции у = кх + 6, используя геометрическое моделирование операций над действительными числами.

Построение <рис. 23).

1) На оси ординат отмечаем коэффициенты к и Ь точками соответственно К(0, к) и В(О, Ь).
2) На оси абсцисс отмечаем точку X(х, 0) и проводим через неё вертикальную прямую, которую будем называть собирательной прямой.
3) На оси ординат строим произведение кх. Для этого строим точку Е = (1,0), точку К соединяем отрезком с точкой Е, а затем через точку X проводим прямую параллельно построенному отрезку. Эта прямая пересечёт ось ординат в точке F(0, кх).
4) Проектируем точку F на собирательную прямую и получаем точку G(x, кх).
5) Отмечаем точку О пересечения осей координат, соединяем отрезком точки О и G, а затем через точку В проводим прямую параллельно отрезку OG. Построенная прямая является искомой. Чтобы в этом убе-

литься, отмечаем точку Я пересечения построенной прямой с собирательной прямой и заставляем её оставлять след. При анимации точки X точка Я вычерчивает прямую, совпадающую с построенной прямой. С другой стороны, эта точка имеет координаты Н(х, кх + 6), а значит вычерчивает прямую у = кх + 6.

Заметим, что точку Я можно построить параллельным переносом точки G на вектор О В (см. живой рис. 23-доп).

Напомним, что коэффициент к прямой у = кх + Ь равен тангенсу угла наклона этой прямой к оси абсцисс, и это можно увидеть, исходя из построений. В самом деле, угол наклона построенной прямой т к оси абсцисс равен углу ZGOX, а тангенс этого угла равен по определению отно-

шению второй координаты точки G к первой координате, то есть — = к.