Геометрический и механический смысл производной уравнение касательной к графику функции

Тема. Производная. Геометрический и механический смысл производной

1. Производная.Рассмотрим некоторую функцию в двух точках и . Здесь через х обозначено некоторое малое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции: называется приращением функции. Производной функции в точке называется предел, к которому стремится отношение приращение функции к приращению аргумента, когда приращение аргумента стремится к нулю (формула 1).

Если этот предел существует, то функция называется дифференцируемой в точке . Производная функции обозначается (формула 2).

1. Геометрический смысл производной. Рассмотрим график функции . Из рис.1 видно, что для любых двух точек A и B графика функции можно записать формула 3). В ней — угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует вывод.

Производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.

1. Уравнение касательной. Выведем уравнение касательной к графику функции в точке . В общем случае уравнение прямой с угловым коэффициентом имеет вид: . Чтобы найти b, воспользуемся тем, что касательная проходит через точку A: . Отсюда следует: . Подставляя это выражение вместо b, получаем уравнение касательной (формула 4).

1. Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси. При этом задан закон движения точки: координата x движущейся точки – это известная функция времени . В течение интервала времени от до точка перемещается на расстояние: . Её средняя скорость () находится по формуле: . При значение средней скорости стремится к определённой величине, которая в физике называется мгновенной скоростью материальной точки в момент времени . Следовательно, для мгновенной скорости можно записать формулу 5. Если сравнить эту формулу с формулой производной 1, то можно сделать вывод, что

Скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по времени:

Видео:Геометрический смысл производной | КасательнаяСкачать

Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной

Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Определения и понятия

Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.

На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.

Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .

Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .

• Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
• Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 α π 2 или 0 ° α 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α > 0 , причем имеется возрастание графика.
• Если α = π 2 , тогда расположение прямой перпендикулярно о х . Равенство задается при помощи равенства x = c со значением с , являющимся действительным числом.
• Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 α π или 90 ° α 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Определение 3

Секущей называют прямую, которая проходит через 2 точки функции f ( x ) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.

По рисунку видно, что А В является секущей, а f ( x ) – черная кривая, α — красная дуга, означающая угол наклона секущей.

Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.

Получаем формулу для нахождения секущей вида:

k = t g α = B C A C = f ( x B ) — f x A x B — x A , где абсциссами точек А и В являются значения x A , x B , а f ( x A ) , f ( x B ) — это значения функции в этих точках.

Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f ( x B ) — f ( x A ) x B — x A или k = f ( x A ) — f ( x B ) x A — x B , причем уравнение необходимо записать как y = f ( x B ) — f ( x A ) x B — x A · x — x A + f ( x A ) или
y = f ( x A ) — f ( x B ) x A — x B · x — x B + f ( x B ) .

Секущая делит график визуально на 3 части: слева от точки А , от А до В , справа от В . На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.

По определению видно, что прямая и ее секущая в данном случае совпадают.

Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.

Касательная к графику функции f ( x ) в точке x 0 ; f ( x 0 ) называется прямая, проходящая через заданную точку x 0 ; f ( x 0 ) , с наличием отрезка, который имеет множество значений х , близких к x 0 .

Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами ( 1 ; 2 ) . Для наглядности, необходимо рассмотреть графики с приближенными к ( 1 ; 2 ) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.

Очевидно, что y = 2 x сливается с прямой у = х + 1 .

Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А . Для наглядности приведем рисунок.

Секущая А В , обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .

Касательной к графику функции y = f ( x ) в точке А считается предельное положение секущей А В при В стремящейся к А , то есть B → A .

Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.

Видео:Геометрический смысл производной. Уравнение касательнойСкачать

Геометрический смысл производной функции в точке

Перейдем к рассмотрению секущей А В для функции f ( x ) , где А и В с координатами x 0 , f ( x 0 ) и x 0 + ∆ x , f ( x 0 + ∆ x ) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f ( x ) = f ( x 0 + ∆ x ) — f ( ∆ x ) . Для наглядности приведем в пример рисунок.

Рассмотрим полученный прямоугольный треугольник А В С . Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f ( x ) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x .

Отсюда следует, что f ‘ ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.

То есть получаем, что f ’ ( x ) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 ( x 0 ) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f ‘ ( x 0 ) .

Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Уравнение касательной прямой

Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.

Уравнение касательной к графику функции y = f ( x ) в точке x 0 , f 0 ( x 0 ) принимает вид y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) .

Имеется в виду, что конечным значением производной f ‘ ( x 0 ) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f ‘ ( x ) = ∞ и lim x → x 0 — 0 f ‘ ( x ) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f ‘ ( x ) ≠ lim x → x 0 — 0 f ‘ ( x ) .

Расположение касательной зависит от значения ее углового коэффициента k x = f ‘ ( x 0 ) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у — k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x 0 .

Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 в точке с координатами ( 1 ; 3 ) с определением угла наклона.

Решение

По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, ( 1 ; 3 ) является точкой касания, тогда x 0 = — 1 , f ( x 0 ) = — 3 .

Необходимо найти производную в точке со значением — 1 . Получаем, что

y ‘ = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 ‘ = = e x + 1 ‘ + x 3 3 ‘ — 6 — 3 3 x ‘ — 17 — 3 3 ‘ = e x + 1 + x 2 — 6 — 3 3 y ‘ ( x 0 ) = y ‘ ( — 1 ) = e — 1 + 1 + — 1 2 — 6 — 3 3 = 3 3

Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.

Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3

Отсюда следует, что α x = a r c t g 3 3 = π 6

Ответ: уравнение касательной приобретает вид

y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) y = 3 3 ( x + 1 ) — 3 y = 3 3 x — 9 — 3 3

Для наглядности приведем пример в графической иллюстрации.

Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.

Выяснить наличие существования касательной к графику заданной функции
y = 3 · x — 1 5 + 1 в точке с координатами ( 1 ; 1 ) . Составить уравнение и определить угол наклона.

Решение

По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.

Перейдем к нахождению производной

y ‘ = 3 · x — 1 5 + 1 ‘ = 3 · 1 5 · ( x — 1 ) 1 5 — 1 = 3 5 · 1 ( x — 1 ) 4 5

Если x 0 = 1 , тогда f ’ ( x ) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( + 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 — 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( — 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке ( 1 ; 1 ) .

Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .

Для наглядности изобразим графически.

Найти точки графика функции y = 1 15 x + 2 3 — 4 5 x 2 — 16 5 x — 26 5 + 3 x + 2 , где

1. Касательная не существует;
2. Касательная располагается параллельно о х ;
3. Касательная параллельна прямой y = 8 5 x + 4 .

Решение

Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ — ∞ ; 2 и [ — 2 ; + ∞ ) . Получаем, что

y = — 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 , x ∈ [ — 2 ; + ∞ )

Необходимо продифференцировать функцию. Имеем, что

y ‘ = — 1 15 x 3 + 18 x 2 + 105 x + 176 ‘ , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 ‘ , x ∈ [ — 2 ; + ∞ ) ⇔ y ‘ = — 1 5 ( x 2 + 12 x + 35 ) , x ∈ — ∞ ; — 2 1 5 x 2 — 4 x + 3 , x ∈ [ — 2 ; + ∞ )

Когда х = — 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:

lim x → — 2 — 0 y ‘ ( x ) = lim x → — 2 — 0 — 1 5 ( x 2 + 12 x + 35 = — 1 5 ( — 2 ) 2 + 12 ( — 2 ) + 35 = — 3 lim x → — 2 + 0 y ‘ ( x ) = lim x → — 2 + 0 1 5 ( x 2 — 4 x + 3 ) = 1 5 — 2 2 — 4 — 2 + 3 = 3

Вычисляем значение функции в точке х = — 2 , где получаем, что

1. y ( — 2 ) = 1 15 — 2 + 2 3 — 4 5 ( — 2 ) 2 — 16 5 ( — 2 ) — 26 5 + 3 — 2 + 2 = — 2 , то есть касательная в точке ( — 2 ; — 2 ) не будет существовать.
2. Касательная параллельна о х , когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f ‘ ( x 0 ) . То есть необходимо найти значения таких х , когда производная функции обращает ее в ноль. То есть значения f ’ ( x ) и будут являться точками касания, где касательная является параллельной о х .

Когда x ∈ — ∞ ; — 2 , тогда — 1 5 ( x 2 + 12 x + 35 ) = 0 , а при x ∈ ( — 2 ; + ∞ ) получаем 1 5 ( x 2 — 4 x + 3 ) = 0 .

— 1 5 ( x 2 + 12 x + 35 ) = 0 D = 12 2 — 4 · 35 = 144 — 140 = 4 x 1 = — 12 + 4 2 = — 5 ∈ — ∞ ; — 2 x 2 = — 12 — 4 2 = — 7 ∈ — ∞ ; — 2 1 5 ( x 2 — 4 x + 3 ) = 0 D = 4 2 — 4 · 3 = 4 x 3 = 4 — 4 2 = 1 ∈ — 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ — 2 ; + ∞

Вычисляем соответствующие значения функции

y 1 = y — 5 = 1 15 — 5 + 2 3 — 4 5 — 5 2 — 16 5 — 5 — 26 5 + 3 — 5 + 2 = 8 5 y 2 = y ( — 7 ) = 1 15 — 7 + 2 3 — 4 5 ( — 7 ) 2 — 16 5 — 7 — 26 5 + 3 — 7 + 2 = 4 3 y 3 = y ( 1 ) = 1 15 1 + 2 3 — 4 5 · 1 2 — 16 5 · 1 — 26 5 + 3 1 + 2 = 8 5 y 4 = y ( 3 ) = 1 15 3 + 2 3 — 4 5 · 3 2 — 16 5 · 3 — 26 5 + 3 3 + 2 = 4 3

Отсюда — 5 ; 8 5 , — 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.

Рассмотрим графическое изображение решения.

Черная линия – график функции, красные точки – точки касания.

1. Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y ‘ ( x ) = 8 5 . Тогда, если x ∈ — ∞ ; — 2 , получаем, что — 1 5 ( x 2 + 12 x + 35 ) = 8 5 , а если x ∈ ( — 2 ; + ∞ ) , тогда 1 5 ( x 2 — 4 x + 3 ) = 8 5 .

Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что

— 1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 — 4 · 43 = — 28 0

Другое уравнение имеет два действительных корня, тогда

1 5 ( x 2 — 4 x + 3 ) = 8 5 x 2 — 4 x — 5 = 0 D = 4 2 — 4 · ( — 5 ) = 36 x 1 = 4 — 36 2 = — 1 ∈ — 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ — 2 ; + ∞

Перейдем к нахождению значений функции. Получаем, что

y 1 = y ( — 1 ) = 1 15 — 1 + 2 3 — 4 5 ( — 1 ) 2 — 16 5 ( — 1 ) — 26 5 + 3 — 1 + 2 = 4 15 y 2 = y ( 5 ) = 1 15 5 + 2 3 — 4 5 · 5 2 — 16 5 · 5 — 26 5 + 3 5 + 2 = 8 3

Точки со значениями — 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .

Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках — 1 ; 4 15 , 5 ; 8 3 .

Возможно существование бесконечного количества касательных для заданных функций.

Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x — π 4 — 1 3 , которые располагаются перпендикулярно прямой y = — 2 x + 1 2 .

Решение

Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется — 1 , то есть записывается как k x · k ⊥ = — 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = — 2 , тогда k x = — 1 k ⊥ = — 1 — 2 = 1 2 .

Теперь необходимо найти координаты точек касания. Нужно найти х , после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y ‘ ( x 0 ) . Из данного равенства найдем значения х для точек касания.

y ‘ ( x 0 ) = 3 cos 3 2 x 0 — π 4 — 1 3 ‘ = 3 · — sin 3 2 x 0 — π 4 · 3 2 x 0 — π 4 ‘ = = — 3 · sin 3 2 x 0 — π 4 · 3 2 = — 9 2 · sin 3 2 x 0 — π 4 ⇒ k x = y ‘ ( x 0 ) ⇔ — 9 2 · sin 3 2 x 0 — π 4 = 1 2 ⇒ sin 3 2 x 0 — π 4 = — 1 9

Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.

3 2 x 0 — π 4 = a r c sin — 1 9 + 2 πk или 3 2 x 0 — π 4 = π — a r c sin — 1 9 + 2 πk

3 2 x 0 — π 4 = — a r c sin 1 9 + 2 πk или 3 2 x 0 — π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 — a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z — множество целых чисел.

Найдены х точек касания. Теперь необходимо перейти к поиску значений у :

y 0 = 3 cos 3 2 x 0 — π 4 — 1 3

y 0 = 3 · 1 — sin 2 3 2 x 0 — π 4 — 1 3 или y 0 = 3 · — 1 — sin 2 3 2 x 0 — π 4 — 1 3

y 0 = 3 · 1 — — 1 9 2 — 1 3 или y 0 = 3 · — 1 — — 1 9 2 — 1 3

y 0 = 4 5 — 1 3 или y 0 = — 4 5 + 1 3

Отсюда получаем, что 2 3 π 4 — a r c sin 1 9 + 2 πk ; 4 5 — 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; — 4 5 + 1 3 являются точками касания.

Ответ: необходимы уравнения запишутся как

y = 1 2 x — 2 3 π 4 — a r c sin 1 9 + 2 πk + 4 5 — 1 3 , y = 1 2 x — 2 3 5 π 4 + a r c sin 1 9 + 2 πk — 4 5 + 1 3 , k ∈ Z

Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.

Рисунок показывает, что расположение функции идет на промежутке [ — 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = — 2 x + 1 2 . Красные точки – это точки касания.

Видео:3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать

Касательная к окружности, эллипсу, гиперболе, параболе

Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.

Касательная к окружности

Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x — x c e n t e r 2 + y — y c e n t e r 2 = R 2 .

Данное равенство может быть записано как объединение двух функций:

y = R 2 — x — x c e n t e r 2 + y c e n t e r y = — R 2 — x — x c e n t e r 2 + y c e n t e r

Первая функция располагается вверху, а вторая внизу, как показано на рисунке.

Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 — x — x c e n t e r 2 + y c e n t e r или y = — R 2 — x — x c e n t e r 2 + y c e n t e r в указанной точке.

Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r — R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r — R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r — R ; y c e n t e r будут являться параллельными о у , тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r — R .

Касательная к эллипсу

Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x — x c e n t e r 2 a 2 + y — y c e n t e r 2 b 2 = 1 .

Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что

y = b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r y = — b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r

Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у . Ниже для наглядности рассмотрим рисунок.

Написать уравнение касательной к эллипсу x — 3 2 4 + y — 5 2 25 = 1 в точках со значениями x равного х = 2 .

Решение

Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что

x — 3 2 4 x = 2 + y — 5 2 25 = 1 1 4 + y — 5 2 25 = 1 ⇒ y — 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5

Тогда 2 ; 5 3 2 + 5 и 2 ; — 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.

Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что

x — 3 2 4 + y — 5 2 25 = 1 y — 5 2 25 = 1 — x — 3 2 4 ( y — 5 ) 2 = 25 · 1 — x — 3 2 4 y — 5 = ± 5 · 1 — x — 3 2 4 y = 5 ± 5 2 4 — x — 3 2

Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 — x — 3 2 , а нижний y = 5 — 5 2 4 — x — 3 2 .

Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид

y ‘ = 5 + 5 2 4 — x — 3 2 ‘ = 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = — 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = — 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = 5 2 3 ( x — 2 ) + 5 3 2 + 5

Получаем, что уравнение второй касательной со значением в точке
2 ; — 5 3 2 + 5 принимает вид

y ‘ = 5 — 5 2 4 — ( x — 3 ) 2 ‘ = — 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = — 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = — 5 2 3 ( x — 2 ) — 5 3 2 + 5

Графически касательные обозначаются так:

Касательная к гиперболе

Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r — α ; y c e n t e r , имеет место задание неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r — b , тогда задается при помощи неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = — 1 .

Гипербола может быть представлена в виде двух объединенных функций вида

y = b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r или y = b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r

В первом случае имеем, что касательные параллельны о у , а во втором параллельны о х .

Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.

Составить уравнение касательной к гиперболе x — 3 2 4 — y + 3 2 9 = 1 в точке 7 ; — 3 3 — 3 .

Решение

Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что

x — 3 2 4 — y + 3 2 9 = 1 ⇒ y + 3 2 9 = x — 3 2 4 — 1 ⇒ y + 3 2 = 9 · x — 3 2 4 — 1 ⇒ y + 3 = 3 2 · x — 3 2 — 4 и л и y + 3 = — 3 2 · x — 3 2 — 4 ⇒ y = 3 2 · x — 3 2 — 4 — 3 y = — 3 2 · x — 3 2 — 4 — 3

Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; — 3 3 — 3 .

Очевидно, что для проверки первой функции необходимо y ( 7 ) = 3 2 · ( 7 — 3 ) 2 — 4 — 3 = 3 3 — 3 ≠ — 3 3 — 3 , тогда точка графику не принадлежит, так как равенство не выполняется.

Для второй функции имеем, что y ( 7 ) = — 3 2 · ( 7 — 3 ) 2 — 4 — 3 = — 3 3 — 3 ≠ — 3 3 — 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.

y ‘ = — 3 2 · ( x — 3 ) 2 — 4 — 3 ‘ = — 3 2 · x — 3 ( x — 3 ) 2 — 4 ⇒ k x = y ‘ ( x 0 ) = — 3 2 · x 0 — 3 x 0 — 3 2 — 4 x 0 = 7 = — 3 2 · 7 — 3 7 — 3 2 — 4 = — 3

Ответ: уравнение касательной можно представить как

y = — 3 · x — 7 — 3 3 — 3 = — 3 · x + 4 3 — 3

Наглядно изображается так:

Касательная к параболе

Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y ( x 0 ) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y ‘ ( x 0 ) · x — x 0 + y ( x 0 ) . Такая касательная в вершине параллельна о х .

Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у . Получаем, что

x = a y 2 + b y + c ⇔ a y 2 + b y + c — x = 0 D = b 2 — 4 a ( c — x ) y = — b + b 2 — 4 a ( c — x ) 2 a y = — b — b 2 — 4 a ( c — x ) 2 a

Графически изобразим как:

Для выяснения принадлежности точки x 0 , y ( x 0 ) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.

Написать уравнение касательной к графику x — 2 y 2 — 5 y + 3 , когда имеем угол наклона касательной 150 ° .

Решение

Начинаем решение с представления параболы в качестве двух функций. Получим, что

— 2 y 2 — 5 y + 3 — x = 0 D = ( — 5 ) 2 — 4 · ( — 2 ) · ( 3 — x ) = 49 — 8 x y = 5 + 49 — 8 x — 4 y = 5 — 49 — 8 x — 4

Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.

k x = y ‘ ( x 0 ) = t g α x = t g 150 ° = — 1 3

Отсюда определим значение х для точек касания.

Первая функция запишется как

y ‘ = 5 + 49 — 8 x — 4 ‘ = 1 49 — 8 x ⇒ y ‘ ( x 0 ) = 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3

Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.

Вторая функция запишется как

y ‘ = 5 — 49 — 8 x — 4 ‘ = — 1 49 — 8 x ⇒ y ‘ ( x 0 ) = — 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3 x 0 = 23 4 ⇒ y ( x 0 ) = 5 — 49 — 8 · 23 4 — 4 = — 5 + 3 4

Имеем, что точки касания — 23 4 ; — 5 + 3 4 .

Ответ: уравнение касательной принимает вид

Видео:Что такое касательная | Осторожно, спойлер! | Борис Трушин |Скачать

Лекция на тему: «Производная функции»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

Видеолекции для
профессионалов

• Свидетельства для портфолио
• Вечный доступ за 120 рублей
• 311 видеолекции для каждого

Раздел 1. Математический анализ

1. Определение производной, ее геометрический и физический смысл.

2. Непрерывность и дифференцируемость функции.

3. Правила вычисления производных.

4. Таблица производных.

5. Производная обратной функции.

6. Производная сложной функции.

7. Применение производных при исследовании функции и построения графиков.

Пусть дана функция у= f ( x ). Разность x — x , называется приращением аргумента и обозначается ∆х= x — x . Разность f ( x )- f ( x ) называется приращением функции и обозначается ∆у

Определение: Производной у или f (х ) от данной функции y = f ( x ) называется предел отношения приращения функции к вызвавшему его приращению аргумента, при условии, что приращение аргумента стремится к нулю: . Обозначается производная f (x) .

Пример. , имеем:

Понятие производной — основное понятие математического анализа. К понятию производной приходится обращаться при решении целого ряда задач физики, механики, геометрии, экономики и ряда других областей.

Выясним геометрический смысл производной. Решим следующую задачу: найдем уравнение касательной к графику функции y = f ( x ) в произвольной его точке Мо(хо, уо). Касательная к произвольной кривой (графику) в некоторой ее точке М₀ определяется следующим образом: возьмем на кривой соседнюю точку Mi , проведем через точки М₀ и M 1 секущую, и будем приближать точку M 1 к точке Мо, двигаясь по кривой; предельное положение М₀Т (если оно существует) секущей Мо M 1 , когда точка М1 сольется с точкой Мо , и определит касательную к данной кривой в точке М₀ .

Итак, касательной к данной кривой в некоторой ее точке М₀ называется прямая, являющаяся предельным положением секущей, проходящей через точку М₀ и соседнюю точку кривой М 1, при условии, что точка M 1, двигаясь по кривой, стремится слиться с точкой М_0.

Итак, точка Мо(хо, yo=f(xo)), точка M .

Угловой коэффициент секущей k , равный тангенсу угла ее наклона к оси Ох, определится так:

Но .

Когда точка стремится к точке , а секущая , стремится занять положение

касательной М₀Т, то угол наклона секущей к оси Ох стремится к углу (наклона

М₀Т к. оси Ox), a стремится к tg (тангенс — функция непрерывная).

Но, когда точка , стремится к точке М₀, 0, или, по определению производной, .

Получим теперь уравнение касательной MoT как уравнение прямой, проходящей через заданную точку графика , угловой коэффициент которой .

Геометрический смысл производной — производная от данной функции при данном значении аргумента равна угловому коэффициенту касательной к графику этой функции в соответствующей точке . Отсюда следует, что f ( x )= R = tgα .

Физический смысл производной заключается в том, что производная от пути по времени есть скорость.

V = S ( t )

Производная функции у = в точке х выражает скорость изменения функции в точке х, т. е. скорость протекания процесса, описываемого зависимостью у = .

Процесс нахождения производной функции называется дифференцированием.

2. Непрерывность и дифференцируемость функции:

Итак,

Но этот предел существует не для всякой функции, а если и существует, то не обязательно при всех значениях ее аргумента, при которых функция определена.

Определение. Функция, имеющая в данной точке производную, называется дифференцируемой в этой точке.

Определение. Функция, имеющая производную во всех точках интервала (а, Ь), называется дифференцируемой в этом интервале.

Теорема. Если функция y=f(x) дифференцируема в точке , то она в этой точке непрерывна.

Доказательство. Пусть аргумент х получает в точке хо приращение не равное нулю. Ему соответствует приращение функции . Рассмотрим очевидное тождество:

. Перейдем к пределу:

откуда и следует непрерывность функции в точке х₀ (функция непрерывна, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции). Итак, необходимым условием дифференцируемости функции является ее непрерывность, то есть всякая дифференцируемая функция непрерывна. Обратное — неверно: не всякая непрерывная функция дифференцируема.

Пример: ; функция непрерывна на всей числовой оси, но в точке х=0 не имеет производной.

.

3. Правила вычисления производных:

1. Производная постоянной равна нулю (С) =0

2. Если функции U и V дифференцируемы, то их сумма и разность дифференцируемы по правилу: ( U + V ) = U + V ; ( U — V ) = U — V ;

3. Если функции U и V дифференцируемы, то их произведение дифференцируемо по правилу: ( UV ) = U V + UV .

4. Если функции U и V дифференцируемы и функция V не равна нулю, то частное дифференцируемо по правилу: ( ) = .

5. Постоянный множитель выносят за знак производной: (С U ) CU

4 .Таблица производных основных функций.

1) Производная степенной функции с натуральным показателем .

2) Производная показательной функции

3) Производная логарифмической функции

4) Производные тригонометрических и обратных тригонометрических функций:

5 . Производная обратной функции:

Определение: Пусть X и Y – некоторые множества и пусть задана функция f , т.е. множество пар чисел (х;у) (х Х; у Y ). Если в этом множестве х и у поменять местами, то получим множество (у;х), которое называется обратной функцией h к функции f

Обратную функцию будем обозначать символом х = h (у).

Из определения следует, что если обратная функция однозначна, то множество значений У функции f является областью определения обратной функции h , а область определения Х функции f – множеством значений обратной функции h .

Теорема1 : Если функция У= f ( x ) определена, строго монотонна и непрерывна на некотором промежутке Х и пусть У – множество ее значений, то на множестве У обратная функция h ( x ) однозначна, строго монотонна и непрерывна.

Теорема2 : Если функция у= f ( x ) имеет в точке х производную , то обратная функция х = h (у) также имеет в соответствующей точке у = производную, причем

h =

6.Производная сложной функции:

Определение: Если на некотором промежутке x определена функция у= f ( u ) с множеством значений у, а на множестве у определена функция у = u ( x ), то функция у = f ( u ( x )) называется сложной функцией.

Производная сложной функции вычисляется по формуле:

y = f ( u ( x )) u ( x ).

Вычислить производную функции у=( 2х+5) , данная функция является сложной.

у =(2х+5) ) =100(2х+5) (2х+5) = 200((2х+5)

7. Применение производных при исследовании функции и построения графиков.

Связь между непрерывностью и дифференцируемостью функции. Если функция f ( x ) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной.

С л е д с т в и е . Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.

Функция y = | x | ( рис.3 ) всюду непрерывна, но она не имеет производной при x = 0 , так как в этой точке не существует касательной к графику этой функции.

Достаточные признаки монотонности функции.

Если f ’( x ) > 0 в каждой точке интервала ( a, b ), то функция f ( x ) возрастает на этом интервале.

Теорема Дарбу : Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.

Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.

Следовательно, функция возрастает на интервалах ( — , 0 ) и ( 1, + ) и убывает на интервале ( 0, 1 ). Точка x = 0 не входит в область определения функции, но по мере приближения x к 0 слагаемое x — 2 неограниченно возрастает, поэтому функция также неограниченно возрастает. В точке x = 1 значение функции равно 3. В соответствии с этим анализом мы можем построить график функции ( рис.4б ) .

Критические точки. Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум ( минимум или максимум , рис.5а,б).

В точках x , x ( рис.5a ) и x ( рис.5b ) производная равна 0; в точка x x ( рис.5б ) производная не существует. Но все они точки экстремума.

Необходимое условие экстремума. Если x — точка экстремума функции f ( x ) и производная f’ существует в этой точке, то f’ (x ) = 0.

Эта теорема — необходимое условие экстремума. Если производная функции в некоторой точке равна 0, то это не значит, что функция имеет экстремум в этой точке. Например, производная функции f ( x ) = x равна 0 при x = 0, но эта функция не имеет экстремум в этой точке ( рис.6)

Достаточные условия экстремума.

Если производная при переходе через точку x меняет свой знак с плюса на минус, то x — точка максимума.

Если производная при переходе через точку x меняет свой знак с минуса на плюс, то x — точка минимума.

План исследования функции .

Для построения графика функции нужно:

1) найти область определения и область значений функции,

2) установить, является ли функция чётной или нечётной,

3) определить, является ли функция периодической или нет,

4) найти нули функции и её значения при x = 0,

5) найти интервалы знакопостоянства,

6) найти интервалы монотонности,

7) найти точки экстремума и значения функции в этих точках,

8) проанализировать поведение функции вблизи “особых” точек

Видео:Касательная к графику функции в точке. 10 класс.Скачать

Геометрический смысл производной. Уравнения касательной и нормали

Определение производной. Ее физический смысл. Определение дифференцируемой функции. Сформулировать теорему о связи между дифференцируемостью и непрерывностью функции.

Производная— основное понятие дифференциального исчесления, характеризующее скорость изменения функции.

Производная — это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

Функцию, имеющую конечную производную, называют дифференцируемой.
Процесс вычисления производной называется дифференцированием

Если положение точки при её движении по числовой прямой задаётся функцией S= f(t), где t– время движения, то производная функции S– мгновенная скорость движения в момент времени t. По аналогии с этой моделью вообще говорят о том, что производная функции у= f(x) – скорость изменения функции в точке х.

Теорема (необходимое условие дифференцируемости функции).Если функция дифференцируема в точке, то она непрерывна в этой точке.

Доказательство. Пусть функция у=f(x) дифференцируема в точке х₀. Дадим в этой точке аргументу приращение Dх. Функция получит приращение Dу. Найдем .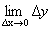

.

Следовательно, у=f(x) непрерывна в точке х₀.

Следствие. Если х₀ – точка разрыва функции, то в ней функция не дифференцируема.

Утверждение, обратное теореме, не верно. Из непрерывности не следует дифференцируемость.

Dх>0, ;

отсюда, b = f ( x₀) – f ’( x₀) · x₀, и подставляя это выражение вместо b, мы получим уравнение касательной:

Нормалью к графику функции y = f (x) в точке A (x₀; y₀) называется прямая, проходящая через точку A и перпендикулярная касательной к этой точке. Она задается уравнением

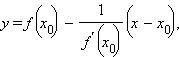что следует из свойства угловых коэффициентов перпендикулярных друг другу прямых.

В случае бесконечной производной касательная в точке x₀ становится вертикальной и задается уравнением x = x₀, а нормаль – горизонтальной: y = y₀.

📺 Видео

Математика без Ху!ни. Уравнение касательной.Скачать

✓ Касательная. Геометрический смысл производной и дифференциала | матан #033 | Борис ТрушинСкачать

03. Геометрический смысл производнойСкачать

Геометрический смысл производной / самое простое объяснениеСкачать

Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

2. Определение производной. Геометрический и физический смысл производной.Скачать

Физический смысл производной. За 40 секСкачать

Уравнение касательнойСкачать

Производная функции. 10 класс.Скачать

Урок 320. Производная функции и ее геометрический смыслСкачать

ЕГЭ. Математика. Геометрический и механический смысл производной. ПрактикаСкачать

Уравнение касательной к графику функции | Алгебра 10 класс #45 | ИнфоурокСкачать

Физический смысл производной 1Скачать