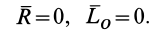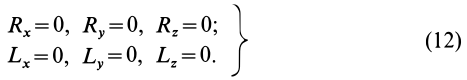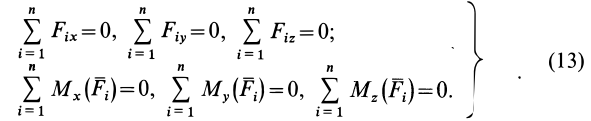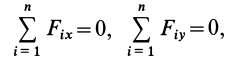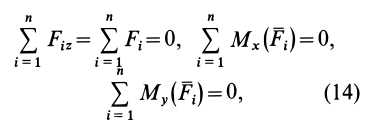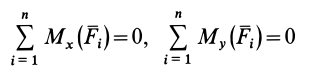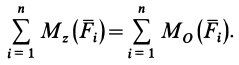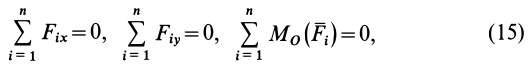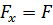Геометрические и аналитические уравнения равновесия

Содержание:

Условия равновесия системы сил:

Видео:4.4 Аналитические уравнения равновесияСкачать

Условия равновесия системы сил в векторной форме

Из теоремы о приведении системы сил к силе и паре сил можно вывести условия равновесия системы сил, действующих на твердое тело. Очевидно, что если система сил находится в равновесии, то в равновесии находится и эквивалентная ей система, состоящая из силы и пары сил. Чтобы такая система сил была эквивалентна _ нулю, необходимо и достаточно равенства нулю как силы

Условия (11) являются векторными условиями равновесия для любой системы сил.

Условия равновесия пространственной системы сил в аналитической форме

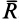
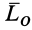
Если при равновесии системы сил, приложенных к твердому телу, главный вектор равен нулю, то его проекция на каждую координатную ось также равна нулю. Это справедливо и для главного момента . Таким образом, из векторных условий равновесия пространственной системы сил следует шесть условий:

Учитывая формулы (5) и (7), эти шесть условий через силы системы выражают в форме

Таким образом, для равновесия пространственной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы три суммы проекций всех сил на оси декартовых координат были равны нулю и три суммы моментов всех сил относительно трех осей координат также были равны нулю.

Из общих условий равновесия для произвольной пространственной системы сил получаются условия равновесия для частных систем сил, приложенных к твердому телу.

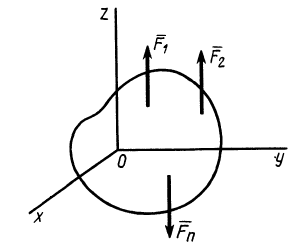
Условия равновесия пространственной системы параллельных сил

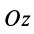
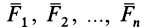
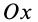
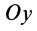
Направим ось параллельно силам (рис. 37). Тогда проекции параллельных сил на перпендикулярные им оси и будут равны нулю и условия

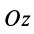
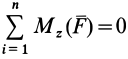
окажутся справедливыми для всех систем параллельных сил, т. е. превратятся в тождества. Момент относительно оси каждой из параллельных сил равен нулю, и условие тоже выполняется для всех систем параллельных сил. Отбрасывая

условия равновесия, которые выполняются тождественно при выбранном направлении оси 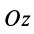, и учитывая, что сумма проекций сил на эту ось является алгебраической суммой сил, из (13) получаем следующие три условия равновесия пространственной системы параллельных сил:

Рис. 37

т. е. для равновесия пространственной системы параллельных сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма этих сил была равна нулю и суммы моментов сил относительно двух координатных осей, перпендикулярных силам, также были равны нулю.

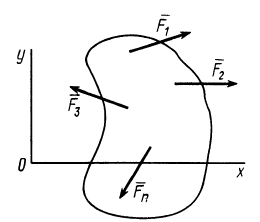
Условия равновесия плоской системы сил

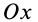
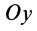
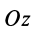
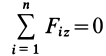
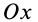
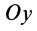
Расположим оси и в плоскости действия сил (рис. 38). Так как ось перпендикулярна силам, то выполняется для всех плоских систем сил, т. е. является тождеством. Каждая из сил расположена в одной плоскости с осями координат и , и поэтому ее моменты относительно этих осей равны нулю. Таким образом, условия равновесия

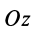
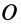
становятся тождествами. Моменты сил относительно оси , перпендикулярной силам, равны алгебраическим моментам этих сил относительно точки . Таким образом,

Из (13) для плоской системы сил после отбрасывания тождеств имеем следующие три условия равновесия:

т. е. для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных осей координат, расположенных в плоскости действия сил, были равны нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости действия сил, также была равна нулю.

Рис. 38

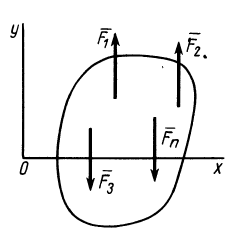
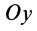
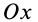
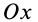
Для плоской системы параллельных сил (рис. 39) одну из осей координат, например , можно выбрать параллельной силам. Тогда сумма проекций параллельных сил на эту ось превратится в алгебраическую сумму сил. Проекция каждой из сил на ось равна нулю; следовательно, сумма проекций сил на ось равна нулю, даже если система сил не находится в равновесии. Это условие выполняется тождественно, и его следует отбросить.

Рис. 39

Итак, для плоской системы параллельных сил из (15) имеем следующие условия равновесия:

т. е. для равновесия плоской системы параллельных сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма сил была равна нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости сил, также была равна нулю.

Из условий равновесия плоской системы сил (15) можно получить и условия равновесия плоской системы сходящихся сил, для чего за моментную точку надо взять точку пересечения линий действия сходящихся сил. Тогда последнее из условий станет тождеством и в качестве условий равновесия для плоской системы сходящихся сил останутся только два первых условия из (15).

• Плоская система сил
• Трение
• Пространственная система сил
• Центр тяжести
• Система сходящихся сил
• Моменты силы относительно точки и оси
• Теория пар сил
• Приведение системы сил к простейшей системе

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

iSopromat.ru

Рассмотрим равновесие пространственной системы сил в аналитической и геометрической форме:

Произвольной пространственной системой сил называется система сил, линии действия которых не лежат в одной плоскости.

Согласно основной теореме статики (теореме Пуансо) любую произвольную систему сил, действующую на твердое тело, можно заменить эквивалентной системой, состоящей из силы (главного вектора системы) и пары сил (главного момента системы сил).

В геометрической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы равнялись нулю

В аналитической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три координатные оси и суммы моментов всех сил относительно этих осей были равны нулю

Условия равновесия могут быть использованы для решения задач на равновесие при определении неизвестных величин (реакций связей).

Чтобы задача была статически определимой, число неизвестных должно быть не более шести.

В частности, для системы параллельных сил условиями равновесия являются следующие равенства

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Статика. Условия равновесия плоской системы сил (23)Скачать

Плоская система сходящихся сил. Условия равновесия в аналитической и геометрической форме

Основные понятия статики

Материальная точка – тело, размерами которого можно пренебречь в условии данной задачи.

Абсолютно твердое тело – тело, в котором расстояние между любыми двумя точками всегда остается неизменным.

Сила –мера механического действия одного материального тела на другое.

1) Точка приложения;

2) Направление действия;

3) Числовое значение (модуль).

F

Единицы измерения: [Н], [кН].

Система сил –несколько сил, действующих на одно твердое тело.

Свободные и несвободные тела. Связи. Классификация связей

Свободным называется тело, которое не скреплено с другими телами и может перемещаться в пространстве.

Пример: самолет, летящий в воздухе; воздушный шар в полете

Несвободным называется тело, перемещение которого в пространстве ограничено другими телами.

Связями называются тела, ограничивающие свободу перемещения данного тела.

Пример: вал, лежащий на подшипниках (вал – несвободное тело, подшипник — связь.

1 тип:связи препятствуют перемещению тела в одном направлении

1) Гладкая поверхность

2) Опорная точка

3) Гибкая нерастяжимая нить

4) Прямолинейный стержень

5) Шарнирно – подвижная опора

2 тип:связи препятствуют перемещению тела по нескольким направлениям

Шарнирно— неподвижная опора

3 тип:связи препятствуют перемещению тела по нескольким направлениям и повороту вокруг своей оси

Проекция силы на ось

Проекцией силы на осьназывается отрезок, лежащий на оси между двумя перпендикулярами, проведенными на ось из начала и конца вектора силы.

Проекция силы на ось равна произведению модуля силы на cos угла между направлением силы и положительным направлением оси.

1) Если направление проекции силы совпадает с положительным направлением оси, то эта проекция положительна.

2) Если направление проекции силы противоположно положительному направлению оси, то эта проекция отрицательна.

3) Если вектор силы параллелен оси, то его проекция на эту ось равна самой силе.

4) Если вектор силы перпендикулярен оси, то его проекция на эту ось равна нулю.

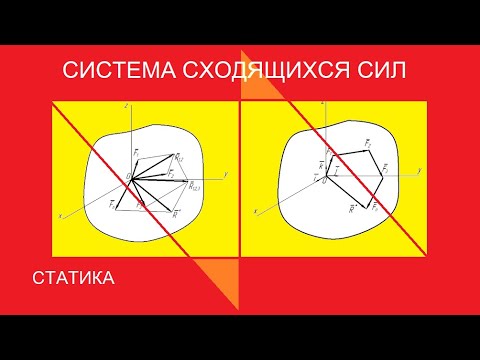
Плоская система сходящихся сил. Условия равновесия в аналитической и геометрической форме

Плоской системой сходящихся сил называется система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке.

Геометрический способ определения равнодействующей – построение силового многоугольника: в произвольно выбранную точку переносится объект равновесия, в эту точку помещается начало первого вектора, перенесенного параллельно самому себе; к концу первого вектора переносится начало второго вектора, к концу второго – начало третьего и т. д.

Геометрическое условие равновесия: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнут.

Аналитическое условие равновесия:для равновесия свободного твердого тела под действием плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех на каждую из осей координат была равна нулю

🎬 Видео

1 Решение задачи графическим и аналитическим методомСкачать

Система сходящихся силСкачать

определение реакций в стержнях от действия грузовСкачать

Химическое равновесие. Константа равновесия. 10 класс.Скачать

Математика это не ИсламСкачать

Статика. Момент сил. Условия равновесия тел | Физика ЕГЭ, ЦТ, ЦЭ | Физика для школьниковСкачать

Урок 82. Равнодействующая параллельных сил. Пара силСкачать

Условия равновесия систем силСкачать

Произвольная плоская система сил. Задача 1Скачать

Три формы уравнений равновесия произвольной плоской системы силСкачать

Система сходящихся сил. Решение задач по МещерскомуСкачать

Термех. Статика. Решение задач на равновесие пространственной системы телСкачать

Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1Скачать

§ 5.1. Уравнения равновесия произвольной системы силСкачать