Генетический алгоритм ga matlab решение нелинейных уравнений

Видео:1 - Решение систем нелинейных уравнений в MatlabСкачать

Генетические алгоритмы в MATLAB

Суть генетических алгоритмов

Данный топик посвящен решению оптимизационных задач при помощи генетических алгоритмов в среде MATLAB. Заранее приношу извинения за большой объем данных: он обусловлен тем, что при написании топика основной поставленной задачей было подробно раскрыть каждый из настраиваемых в MATLAB параметров работы генетических алгоритмов.

Генетические алгоритмы – это метод решения оптимизационных задач, основанный на биологических принципах естественного отбора и эволюции. Генетический алгоритм повторяет определенное количество раз процедуру модификации популяции (набора отдельных решений), добиваясь тем самым получения новых наборов решений (новых популяций). При этом на каждом шаге из популяции выбираются «родительские особи», то есть решения, совместная модификация которых (скрещивание) и приводит к формированию новой особи в следующем поколении. Генетический алгоритм использует три вида правил, на основе которых формируется новое поколение: правила отбора, скрещивания и мутации. Мутация позволяет путем внесения изменений в новое поколение избежать попадания в локальные минимумы оптимизируемой функции.

(Под катом основная часть + несколько скриншотов).

Механизм работы с генетическими алгоритмами в среде MATLAB реализован двумя способами:

1. Вызов функции генетических алгоритмов
2. Использование комплекта Genetic Algorithm Tool

Оба способа поставляются в числе стандартного набора функций и модулей MATLAB. На мой взгляд, намного более удобным и наглядным является второй способ работы с генетическими алгоритмами в MATLAB, связанный с использованием модуля Genetic Algorithm Tool. Его и рассмотрим подробнее.

Работа с GENETIC ALGORITHM TOOL

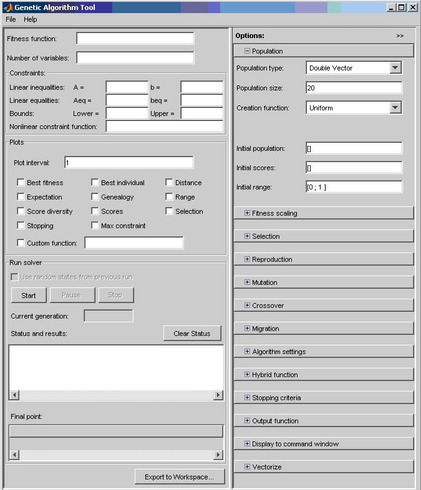
Для запуска пакета Genetic Algorithm Tool следует в командной строке MATLAB выполнить команду gatool. После этого запустится пакет генетических алгоритмов и на экране появится основное окно утилиты.

В поле Fitness function указывается оптимизируемая функция в виде @fitnessfun, где fitnessfun.m – название M-файла, в котором предварительно следует описать оптимизируемую функцию. На всякий случай отмечу, что M-файл создается в среде MATLAB через меню File->New->M-File. Пример описания некоторой функции my_fun в M-файле:

function z = my_fun(x)
z = x(1)^2 — 2*x(1)*x(2) + 6*x(1) + x(2)^2 — 6*x(2);

Вернемся к основному окну утилиты GATool. В поле Number of variables указывается длина входного вектора оптимизируемой функции. В рассмотренном выше примере функция my_fun имеет входной вектор длины 2.
В панели Constraints можно задать ограничения или ограничивающую нелинейную функцию. В поле Linear inequalities задается линейное ограничение неравенством вида:

В поле Linear equalities данной панели задаются линейные ограничения равенством:

В обоих случаях A – некоторая матрица, b – вектор.

В поле Bounds в векторном виде задаются нижнее и верхнее ограничения переменных, а в поле Nonlinear constraint function можно задать произвольную нелинейную функцию ограничений.

Если в конкретной задаче не требуется задание ограничений, все поля панели Constraints следует оставить незаполненными.

Ниже находится панель настройки графиков. Она позволяет выводить различные графики, отображающие информацию о работе генетического алгоритма. На основе этой информации можно менять настройки алгоритма с целью повышения эффективности его работы. Например, выбор опции Best Fitness в этой панели позволяет вывести на одном графике лучшее и среднее значение оптимизируемой функции для каждого поколения работы алгоритма. Подробнее эта панель будет описана ниже наравне с остальными панелями вкладки Options утилиты GATool.

Панель Run Solver содержит управляющие элементы (кнопки Start, Pause и Stop для начала, временной и полной остановки работы генетического алгоритма). Также она содержит поля Status and results, в которое выводятся текущие результаты работы запущенного генетического алгоритма, и Final point, в котором выводится значение конечной точки работы алгоритма — наилучшей величины оптимизируемой функции (то есть, искомое значение).

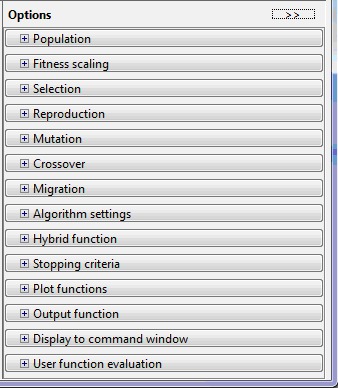
В правой части основного окна утилиты GATool находится панель Options. Она позволяет устанавливать различные настройки для работы генетических алгоритмов. При щелчке мышью по кнопкам [+], которые находятся напротив названия каждого из настраиваемых параметров в панели Options, появляются выпадающие списки (вкладки), содержащие поля для ввода и изменения соответствующих параметров генетического алгоритма.

Основными настраиваемыми параметрами в GATool являются:
— популяция (вкладка Population);
— масштабирование (вкладка Fitness Scaling);
— оператор отбора (вкладка Selection);
— оператор репродукции (вкладка Reproduction);
— оператор мутации (вкладка Mutation);
— оператор скрещивание (вкладка Crossover);
— перенесение особей между популяциями (вкладка Migration);
— специальные параметры алгоритма (вкладка Algorithm settings);
— задание гибридной функции (вкладка Hybrid function);
— задание критерия остановки алгоритма (вкладка Stopping criteria);
— вывод различной дополнительной информации по ходу работы генетического алгоритма (вкладка Plot Functions);
— вывод результатов работы алгоритма в виде новой функции (вкладка Output function);
— задание набора информации для вывода в командное окно (вкладка Display to command window);
— способ вычисления значений оптимизированной и ограничивающей функций (вкладка User function evaluation).

Рассмотрим подробнее все вышеперечисленные вкладки панели Options и элементы, которые они содержат.

Во вкладке настройки популяций пользователь имеет возможность выбрать тип математических объектов, к которому будут относиться особи всех популяций (двойной вектор, битовая строка или пользовательский тип). При этом стоит учитывать, что использование битовой строки и пользовательских типов накладывают ограничения на перечень допустимых операторов создания, мутации и скрещивания особей. Так, например, при выборе в качестве формы представления особей битовой строки для оператора скрещивания нельзя использовать гибридную функцию или нелинейную ограничивающую функцию.
Также вкладка популяции позволяет настраивать размер популяции (из скольких особей будет состоять каждое поколение) и каким образом будет создаваться начальное поколение (Uniform – если отсутствуют накладываемые ограничения, в противном случае — Feasible population). Кроме того, в рассматриваемой вкладке имеется возможность задать вручную начальное поколение (используя пункт Initial population) или его часть, начальный рейтинг особей (пункт Initial scores), а также ввести ограничительный числовой диапазон, которому должны принадлежать особи начальной популяции (Initial range).

Во вкладке масштабирования (Fitness Scaling) пользователь имеет возможность указать функцию масштабирования, которая конвертирует достигаемые оптимизируемой функцией значения в значения, лежащие в пределах, допустимых для оператора отбора. При выборе в качестве функции масштабирования параметра Rank масштабирование будет приводиться к рейтингу, то есть особям присваивается рейтинговый номер (для лучшей особи – единица, для следующей – двойка, и так далее). Пропорциональное масштабирование (Proportional) задает вероятности пропорционально заданному числовому ряду для особей. При выборе опции Top наибольшее рейтинговое значение присваивается сразу нескольким наиболее выдающимся особям (их число указывается в виде параметра). Наконец, при выборе масштабирования типа Shift linear имеется возможность указать максимальную вероятность наилучшей особи.

Вкладка Selection позволяет выбрать оператор отбора родительских особей на основе данных из функции масштабирования. В качестве доступных для выбора вариантов оператора отбора предлагаются следующие:

— Tournament – случайно выбирается указанное число особей, среди них на конкурсной основе выбираются лучшие;
— Roulette – имитируется рулетка, в которой размер каждого сегмента устанавливается в соответствии с его вероятностью;
— Uniform – родители выбираются случайным образом согласно заданному распределению и с учетом количества родительских особей и их вероятностей;
— Stochastic uniform – строится линия, в которой каждому родителю ставится в соответствие её часть определенного размера (в зависимости от вероятности родителя), затем алгоритм пробегает пот линии шагами одинаковой длины и выбирает родителей в зависимости от того, на какую часть линии попал шаг.

Вкладка Reproduction уточняет каким образом происходит создание новых особей. Пункт Elite count позволяет указать число особей, которые гарантировано перейдут в следующее поколение. Пункт Crossover fraction указывает долю особей, которые создаются путем скрещивания. Остальная доля создается путем мутации.

Во вкладке оператора мутации выбирается тип оператора мутации. Доступны следующие варианты:

— Gaussian – добавляет небольшое случайное число (согласно распределению Гаусса) ко всем компонентам каждого вектора-особи;
— Uniform – выбираются случайным образом компоненты векторов и вместо них записываются случайные числа из допустимого диапазона;
— Adaptive feasible – генерирует набор направлений в зависимости от последних наиболее удачных и неудачных поколений и с учетом налагаемых ограничений продвигается вдоль всех направлений на разную длину;
— Custom – позволяет задать собственную функцию.

Вкладка Crossover позволяет выбрать тип оператора скрещивания (одноточечное, двухточечное, эвристическое, арифметическое или рассеянное (Scattered), при котором генерируется случайный двоичный вектор соответствия родителей). Также имеется возможность задания произвольной (custom) функции скрещивания.

Во вкладке Migration можно настраивать правила, согласно которым особи будут перемещаться между подпопуляциями в пределах одной популяции. Подпопуляции создаются, если в качестве размера популяции указан вектор, а не натуральное значение. В данной вкладке можно указать направление миграции (forward – в следующую подпопуляцию, both – в предыдущую и следующую), долю мигрирующих особей и частоту миграции (сколько поколений проходит между миграциями). Если создание подпопуляций не требуется, эту вкладку всегда стоит оставлять без изменений.

Вкладка специальных опций алгоритма позволяет настраивать параметры решения системы нелинейных ограничений, налагаемых на алгоритм. Значение параметра Initial penalty определяет начальное числовое значение критики алгоритма, Penalty factor используется как множитель этого значения в случаях, когда разработчика не устраивает точность оптимизации или при выходе за границы, определенные во вкладке ограничений. Как правило, эти опции детально настраиваются для решения задач высокой сложности.

Вкладка Hybrid function позволяет задать ещё одну функцию минимизации, которая будет использоваться после окончания работы алгоритма. В качестве возможных гибридных функций доступны следующие встроенные в саму среду MATLAB функции:
− none (не использовать гибридную функцию);
− fminsearch (поиск минимального из значений);
− patternsearch (поиск по образцу);
− fminunc (для неограниченного алгоритма);
− fmincon (для алгоритма с заданными ограничениями).

Во вкладке критерия остановки (Stopping criteria) указываются ситуации, при которых алгоритм совершает остановку. При этом, настраиваемыми являются следующие параметры:

— Generations – максимальное число поколений, после превышения которого произойдет остановка;
— Time limit – лимит времени на работу алгоритма;
— Fitness limit – если оптимизируемое значение меньше или равно данного лимита, то алгоритм остановится;
— Stall generations – количество мало отличающихся поколений, по прошествии которых алгоритм остановится;
— Stall time limit – то же, что и предыдущий параметр, но применимо к времени работы алгоритма;
— Function tolerance и Nonlinear constraint tolerance – минимальные значения изменений оптимизируемой и ограничивающей функций соответственно, при которых алгоритм продолжит работу.

Особый интерес представляет вкладка Plot Functions, которая позволяет выбирать различную информацию, которая выводится по ходу работы алгоритма и показывает как корректность его работы, так и конкретные достигаемые алгоритмом результаты. Наиболее важными и используемыми для отображения параметрами являются:

— Plot interval – число поколений, по прошествии которого происходит очередное обновление графиков;
— Best fitness – вывод наилучшего значения оптимизируемой функции для каждого поколения;
— Best individual – вывод наилучшего представителя поколения при наилучшем оптимизационном результате в каждом из поколений;
— Distance – вывод интервала между значениями особей в поколении;
— Expectation – выводит ряд вероятностей и соответствующие им особи поколений;
— Genealogy – вывод генеалогического дерева особей;
— Range – вывод наименьшего, наибольшего и среднего значений оптимизируемой функции для каждого поколения;
— Score diversity – вывести гистаграмму рейтинга в каждом поколении;
— Scores – вывод рейтинга каждой особи в поколении;
— Selection – вывод гистограммы родителей;
— Stopping – вывод информации о состоянии всех параметров, влияющих на критерии остановки;
— Custom – отображение на графике некоторой указанной пользователем функции.

Вкладка вывода результатов в виде новой функции (Output function) позволяет включить вывод истории работы алгоритма в отдельном окне с заданным интервалом поколений (флаг History to new window и поле Interval соответственно), а также позволяет задать и вывести произвольную выходную функцию, задаваемую в поле Custom function.

Вкладка User function evaluation описывает, в каком порядке происходит вычисление значений оптимизируемой и ограничивающей функций (отдельно, параллельно в одном вызове или одновременно).

Наконец, вкладка Display to command window позволяет настраивать информацию, которая отображается в основном командном окне MATLAB при работе алгоритма. Возможны следующие значения: Off — нет вывода в командное окно, Iterative — вывод информации о каждой итерации работающего алгоритма, Diagnose — вывод информации о каждой итерации и дополнительных сведениях о возможных ошибках и измененных ключевых параметрах алгоритма, Final – выводится только причина остановки и конечное значение.

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Генетические алгоритмы в MatLab

ЛАБОРАТОРНАЯ РАБОТА № 2

Генетические алгоритмы в MatLab

Цель работы: изучение основ работы с Genetic Algorithm в MatLAB, исследование экстремумов функций с помощью генетических алгоритмов.

Общие сведения о генетических алгоритмах

Генетические алгоритмы – это метод решения оптимизационных задач, основанный на биологических принципах естественного отбора и эволюции. Генетический алгоритм повторяет определенное количество раз процедуру модификации популяции (набора отдельных решений), добиваясь тем самым получения новых наборов решений (новых популяций). При этом на каждом шаге из популяции выбираются «родительские особи», то есть решения, совместная модификация которых (скрещивание) и приводит к формированию новой особи в следующем поколении. Генетический алгоритм использует три вида правил, на основе которых формируется новое поколение: правила отбора, скрещивания и мутации. Мутация позволяет путем внесения изменений в новое поколение избежать попадания в локальные минимумы оптимизируемой функции.

Данные алгоритмы основаны на принципах естественного отбора Ч. Дарвина и предложены относительно недавно – в 1975 году Джоном Холландом. В них используются как аналог механизма генетического наследования, так и аналог естественного отбора. При этом сохраняется биологическая терминология в упрощенном виде и основные понятия линейной алгебры.

Генетические алгоритмы оптимизации являются алгоритмами случайно-направленного поиска и применяются в основном там, где сложно или невозможно сформулировать задачу в виде, пригодном для более быстрых алгоритмов локальной оптимизации, либо если стоит задача оптимизации недифференцируемой функции или задача многоэкстремальной глобальной оптимизации.

Типичными применениями ГА являются следующие:

оптимизация функций; оптимизация запросов в базах данных; задачи на графах (задача коммивояжера, раскраска, нахождение паросочетаний); настройка и обучение искусственной нейронной сети; задачи компоновки; составление расписаний; игровые стратегии; теория приближений и др.

Основной идеей ГА является организация «борьбы за существование» и «естественный отбор» среди пробных (примерных) решений задачи. Поскольку ГА используют биологические аналогии, то применяющаяся терминология напоминает биологическую. Как известно, эволюционная теория утверждает, что жизнь на нашей планете возникла вначале лишь в простейших ее формах – в виде одноклеточных организмов. Эти формы постепенно усложнялись, приспосабливаясь к окружающей среде и порождая новые виды, и только через многие миллионы лет появились первые животные и люди. Можно сказать, что каждый биологический вид с течением времени улучшает свои качества так, чтобы наиболее эффективно справляться с важнейшими задачами выживания, самозащиты, размножения и т. д. Таким путем возникла защитная окраска у многих рыб и насекомых, панцирь у черепахи, яд у скорпиона и многие другие полезные приспособления.

Такие алгоритмы чаще всего используются в случае, когда искомая целевая функция является разрывной, существенно нелинейной, стохастической и не имеет производных или эти производные являются недостаточно определенными. Собственно генетические алгоритмы относятся к разделу Genetic Algorithm и вызываются из командной строки с помощью gatool.

Основными параметрами ГА являются:

вероятность мутации; точность получения результата; количество итераций алгоритма или количество поколений; размер популяции.

Генетический алгоритм работает согласно следующей схеме:

Прежде всего, в данном алгоритме для организации начала счета создается произвольное исходное семейство. Далее алгоритм производит некую последовательность новых семейств или поколений. На каждом отдельном шаге алгоритм использует определенные индивидуумы из текущего поколения, для того, что бы создать последующее поколение. При формировании нового поколения в алгоритме проводятся следующие действия:

Отмечается каждый член текущего семейства посредством вычисления соответствующего значения пригодности; Проводится масштабирование полученного ряда значений функции пригодности, что позволяет построить диапазон значений более удобный для последующего использования; Выбираются родительские значения на основе значений их пригодности; Часть индивидуумов из родительского поколения имеет более меньшие значения функции пригодности и которые в далее выбираются как элитные значения. Эти элитные значения передаются далее уже в последующее поколение; Дочерние значения образуются или путем неких случайных изменений отдельного одного родителя — мутация — или путем комбинации векторных компонентов некой пары родителей – кроссовер; Замена текущего семейства на дочернее с целью формирования последующего поколения.

Останов алгоритма производится тогда, когда выполняется какой-нибудь критерий останова.

Также основной принцип работы ГА можно описать по схеме, представленной на рис. 1.

Генерируем начальную популяцию из n хромосом; Вычисляем для каждой хромосомы ее пригодность; Выбираем пару хромосом-родителей с помощью одного из способов отбора; Проводим кроссинговер двух родителей с вероятностью , производя двух потомков; Проводим мутацию потомков с вероятностью ; Повторяем шаги 3–5, пока не будет сгенерировано новое поколение популяции, содержащее n хромосом; Повторяем шаги 2–6, пока не будет достигнут критерий окончания процесса.

Рис. 1. Схема работы генетического алгоритма

Условия останова алгоритма:

Для определения условий останова в генетическом алгоритме используются следующие пять условий:

Generations – алгоритм останавливается тогда, когда число поколений достигает некоего заданного значения Generations.

Time limit – алгоритм останавливается по истечению некоего заданного времени в секундах Time limit.

Fitness limit – алгоритм останавливается тогда, когда значение функции пригодности для наилучшей точки для текущего семейства будет меньше или равно Fitness limit.

Stall generations – алгоритм останавливается в случае, если нет улучшения для целевой функции в последовательности следующих друг за другом поколений длиной Stall generations.

Stall time limit – алгоритм останавливается в случае, если нет улучшения для целевой функции в течение интервала времени в секундах равного Stall time limit.

После процесса воспроизводства происходят мутации (mutation). Данный оператор необходим для «выбивания» популяции из локального экстремума и препятствует преждевременной сходимости. Это достигается за счет того, что изменяется случайно выбранный ген в хромосоме (рис. 2).

Рис. 2. Мутация в точке

Используемая по умолчанию функция Гауссовской мутации добавляет случайно выбранное с помощью распределения Гаусса число, mutation, к каждому элементу родительского вектора. Как правило, это число мутаций, которое пропорционально стандартному среднеквадратичному отклонению от распределения, уменьшается с каждой последующей итерацией. В алгоритме путем установки опций Scale и Shrink имеется возможность управлять усредненным числом мутаций для каждой итерации:

Опция Scale управляет стандартным среднеквадратичным отклонением на первой итерации, которое равно параметру Scale, умноженному на ранг исходного семейства, задаваемого с помощью опции Initial range. Опция Shrink управляет скоростью уменьшения среднего числа мутаций. Стандартное среднеквадратичное отклонение линейно уменьшается до тех пор, пока его конечное значение будет равно 1 – Shrink от его начального значения для первого поколения. Например, если величина Shrink по умолчанию принимается равной 1, то тогда число мутаций уменьшается к конечному шагу до нуля.

Кроссовер (скрещивание) – это операция, при которой из двух хромосом порождается одна или несколько новых хромосом. В простейшем случае кроссовер в генетическом алгоритме реализуется так же, как и в биологии. При этом хромосомы разрезаются в случайной точке и обмениваются частями между собой. Например, если хромосомы (1, 2, 3, 4, 5) и (0, 0, 0, 0, 0) разрезать между третьим и четвертым генами и обменять их части, то получатся потомки (1, 2, 3, 0, 0) и (0, 0, 0, 4, 5).

Установка без мутаций/ установка без кроссовера

Для того, что проконтролировать работу Генетического алгоритма без включения операции мутации, следует установить параметр Crossover fraction из вкладки Reproduction в 1.0.

Для того, что проконтролировать работу Генетического алгоритма без включения операции кроссовера, следует установить параметр Crossover fraction в 0.

Реализация генетических алгоритмов в MatLAB

Для запуска пакета Genetic Algorithm Tool следует в командной строке MATLAB выполнить команду gatool. После этого запустится пакет генетических алгоритмов и на экране появится основное окно утилиты (рис. 3).

Рис. 3. Окно утилиты Genetic Algorithm Tool

Для того чтобы ввести необходимую для решения задачу следует заполнить два поля:

Fitness function – подлежащая минимизации функция. Следует ввести указатель на М-файл функции. Number of variables – число независимых переменных для функции пригодности.

Пример заполнения выше описанных полей приведен на рис. 4. Функция минимизации в данном случае двумерна и имеет имя rozenbr_fun.

Рис. 4. Пример заполнения полей

М-файл с целевой функцией должен находиться в одной из папок доступа MatLAB, либо пользователь сам может внести в каталог поиска MatLAB с помощью следующей последовательности действий: Основное окно MatLAB -> File -> Set Path -> Add Folder -> Save.

Для начала работы с Генетическим алгоритмом следует кликнуть на кнопку Start, которая расположена на панели Run solver and view results.

В поле Current iteration выводится текущее число поколений. После окончания работы алгоритма на поле ниже выводится значение функции в конечной найденной точке, а на поле Final point соответственно координаты этой точки.

В правой части окна ГА расположена панель Options. Она позволяет устанавливать различные настройки для работы генетических алгоритмов. Основные вкладки, которые необходимы для работы с ГА:

популяция (вкладка Population); оператор отбора (вкладка Selection); оператор репродукции (вкладка Reproduction); оператор мутации (вкладка Mutation); оператор скрещивание (вкладка Crossover); задание критерия остановки алгоритма (вкладка Stopping criteria); вывод различной дополнительной информации по ходу работы генетического алгоритма (вкладка Plot Functions).

Опишем возможности этих вкладок более подробно:

Во вкладке настройки популяций пользователь имеет возможность выбрать тип математических объектов, к которому будут относиться особи всех популяций (двойной вектор, битовая строка или пользовательский тип). Также вкладка популяции позволяет настраивать размер популяции (из скольких особей будет состоять каждое поколение) – поле Population size. Кроме того, в рассматриваемой вкладке имеется возможность задать вручную начальное поколение (используя пункт Initial population) или его часть, начальный рейтинг особей (пункт Initial scores), а также ввести ограничительный числовой диапазон, которому должны принадлежать особи начальной популяции (Initial range).

Вкладка Selection позволяет выбрать оператор отбора родительских особей на основе данных из функции масштабирования. В качестве доступных для выбора вариантов оператора отбора предлагаются следующие:

Tournament – случайно выбирается указанное число особей, среди них на конкурсной основе выбираются лучшие; Roulette – имитируется рулетка, в которой размер каждого сегмента устанавливается в соответствии с его вероятностью; Uniform – родители выбираются случайным образом согласно заданному распределению и с учетом количества родительских особей и их вероятностей; Stochastic uniform – строится линия, в которой каждому родителю ставится в соответствие её часть определенного размера (в зависимости от вероятности родителя), затем алгоритм пробегает пот линии шагами одинаковой длины и выбирает родителей в зависимости от того, на какую часть линии попал шаг.

Вкладка Reproduction уточняет каким образом происходит создание новых особей. Пункт Elite count позволяет указать число особей, которые гарантировано перейдут в следующее поколение. Пункт Crossover fraction указывает долю особей, которые создаются путем скрещивания. Остальная доля создается путем мутации.

Во вкладке оператора мутации выбирается тип оператора мутации. Доступны следующие варианты:

Gaussian – добавляет небольшое случайное число (согласно распределению Гаусса) ко всем компонентам каждого вектора-особи; Uniform – выбираются случайным образом компоненты векторов и вместо них записываются случайные числа из допустимого диапазона; Adaptive feasible – генерирует набор направлений в зависимости от последних наиболее удачных и неудачных поколений и с учетом налагаемых ограничений продвигается вдоль всех направлений на разную длину; Custom – позволяет задать собственную функцию.

Вкладка Crossover позволяет выбрать тип оператора скрещивания (одноточечное, двухточечное, эвристическое, арифметическое или рассеянное (Scattered), при котором генерируется случайный двоичный вектор соответствия родителей). Также имеется возможность задания произвольной (custom) функции скрещивания.

Во вкладке критерия остановки (Stopping criteria) указываются ситуации, при которых алгоритм совершает остановку (см. Условия останова алгоритма).

Вкладка Plot Functions, которая позволяет выбирать различную информацию, которая выводится по ходу работы алгоритма и показывает как корректность его работы, так и конкретные достигаемые алгоритмом результаты. Наиболее важными и используемыми для отображения параметрами являются:

Best fitness – вывод наилучшего значения оптимизируемой функции для каждого поколения; Best individual – вывод наилучшего представителя поколения при наилучшем оптимизационном результате в каждом из поколений; Distance – вывод интервала между значениями особей в поколении.

Пример поиска глобального минимума

Рассмотрим принцип работы генетических алгоритмов на примере сложной функции. Определим минимум функции Розенброка, определяемой как:

График функции Розенброка представлен ниже на рис. 5.

Рис. 5. График функции Розенброка

Как видно из графика, функция Розенброка содержит несколько локальных минимумов. Однако функция имеет только один глобальный минимум, который находится в точке с координатами (1;1). Значение функции в этой точке .

Определим глобальный минимум с помощью одного из методов поиска многомерной оптимизации – метод Хука-Дживса. На рис. 6 приведен алгоритм поиска по методу Хука-Дживса, реализованный с помощью MathLAB.

Рис. 6. Поиск минимума методом Хука-Дживса

Из результатов работы алгоритма по поиску минимума функции видно, что истинный глобальный минимум не найден, а определен лишь локальный минимум. Существуют множество других схожих методов, к примеру, градиентный метод. Все они работают очень быстро, но не гарантируют оптимальности найденного решения. Они идеальны для применения в так называемых унимодальных задачах, где целевая функция имеет единственный локальный минимум (максимум), он же является глобальным.

Таким образом, можно сделать вывод, что задача оптимизации по нахождению минимума сложной функции не всегда может быть решена с помощью стандартных методов оптимизации.

Проведем исследование этой же функции с помощью генетических алгоритмов в MatLAB.

Напишем M-файл для данной функции и сохраним его под именем rozenbr_fun. m (рис. 7).

Рис. 7. M-файл с целевой функцией

В поле fitness function введем имя целевой функции @rozenbr_fun.

Установим количество особей в популяции = 10, в разделе plots установим флажки для best fitness, best individual, distance. Щелкнем по кнопке start.

Для данной задачи результаты получились следующие — минимум функции достигается в точке с координатами Значение функции Розенброка в этой точке .

Графическое решение приведено на рис. 8.

Рис. 8. Графическое решение задачи

Первый график (Fitness Value) отображает изменение значение целевой функции. Видно, что, начиная с 40 популяции, алгоритм сошелся к решению. На втором графике (Current best individual) изображена наилучшая особь. Третий график (Average Distance) соответствует изменению расстояния между особями в поколениях.

Конечная точка расчетов близка к точке истинного минимума (1, 1). Исследуем функцию при различных исходных данных, результаты приведены в табл. 1. Количество итераций алгоритма или количество поколений является остановом алгоритма, его значение оставим по умолчанию равным 100 поколениям. Тип оператора мутации выберем Гауссов с вероятностью 1%.

Таблица 1. Результаты эксперимента по нахождению минимума

Видео:Генетический алгоритмСкачать

Генетический алгоритм ga matlab решение нелинейных уравнений

Find minimum of function using genetic algorithm

Видео:#1. Основные этапы работы генетического алгоритма | Генетические алгоритмы на PythonСкачать

Syntax

Видео:#4. Как генетический алгоритм находит решения. Преимущества и недостатки | Генетические алгоритмыСкачать

Description

x = ga( fun , nvars ) finds a local unconstrained minimum, x , to the objective function, fun . nvars is the dimension (number of design variables) of fun .

Note

Passing Extra Parameters explains how to pass extra parameters to the objective function and nonlinear constraint functions, if necessary.

x = ga( fun , nvars , A , b ) finds a local minimum x to fun , subject to the linear inequalities A*x ≤ b . ga evaluates the matrix product A*x as if x is transposed ( A*x’ ).

x = ga( fun , nvars , A , b , Aeq , beq ) finds a local minimum x to fun , subject to the linear equalities Aeq*x = beq and A*x ≤ b . (Set A=[] and b=[] if no linear inequalities exist.) ga evaluates the matrix product Aeq*x as if x is transposed ( Aeq*x’ ).

x = ga( fun , nvars , A , b , Aeq , beq , lb , ub ) defines a set of lower and upper bounds on the design variables, x , so that a solution is found in the range lb ≤ x ≤ ub . (Set Aeq=[] and beq=[] if no linear equalities exist.)

x = ga( fun , nvars , A , b , Aeq , beq , lb , ub , nonlcon ) subjects the minimization to the constraints defined in nonlcon . The function nonlcon accepts x and returns vectors C and Ceq , representing the nonlinear inequalities and equalities respectively. ga minimizes the fun such that C(x) ≤ 0 and Ceq(x) = 0 . (Set lb=[] and ub=[] if no bounds exist.)

x = ga( fun , nvars , A , b , Aeq , beq , lb , ub , nonlcon , options ) minimizes with the default optimization parameters replaced by values in options . (Set nonlcon=[] if no nonlinear constraints exist.) Create options using optimoptions .

x = ga( fun , nvars , A , b , Aeq , beq , lb , ub , nonlcon , intcon ) or x = ga( fun , nvars , A , b , Aeq , beq , lb , ub , nonlcon , intcon , options ) requires that the variables listed in intcon take integer values.

Note

When there are integer constraints, ga does not accept nonlinear equality constraints, only nonlinear inequality constraints.

x = ga( problem ) finds the minimum for problem , a structure described in problem .

[ x , fval ] = ga( ___ ) , for any previous input arguments, also returns fval , the value of the fitness function at x .

[ x , fval , exitflag , output ] = ga( ___ ) also returns exitflag , an integer identifying the reason the algorithm terminated, and output , a structure that contains output from each generation and other information about the performance of the algorithm.

[ x , fval , exitflag , output , population , scores ] = ga( ___ ) also returns a matrix population , whose rows are the final population, and a vector scores , the scores of the final population.

Видео:Генетические алгоритмы в MATLAB. Global Optimization ToolboxСкачать

Examples

Optimize a Nonsmooth Function Using ga

The ps_example.m file ships with your software. Plot the function.

Find the minimum of this function using ga .

Minimize a Nonsmooth Function with Linear Constraints

Use the genetic algorithm to minimize the ps_example function on the region x(1) + x(2) >= 1 and x(2) .

First, convert the two inequality constraints to the matrix form A*x . In other words, get the x variables on the left-hand side of the inequality, and make both inequalities less than or equal:

Solve the constrained problem using ga .

The constraints are satisfied to within the default value of the constraint tolerance, 1e-3 . To see this, compute A*x’ — b , which should have negative components.

Minimize a Nonsmooth Function with Linear Equality and Inequality Constraints

Use the genetic algorithm to minimize the ps_example function on the region x(1) + x(2) >= 1 and x(2) == 5 + x(1) .

First, convert the two constraints to the matrix form A*x and Aeq*x = beq . In other words, get the x variables on the left-hand side of the expressions, and make the inequality into less than or equal form:

Solve the constrained problem using ga .

Check that the constraints are satisfied to within the default value of ConstraintTolerance , 1e-3 .

Optimize with Linear Constraints and Bounds

Use the genetic algorithm to minimize the ps_example function on the region x(1) + x(2) >= 1 and x(2) == 5 + x(1) . In addition, set bounds 1 and -3 .

First, convert the two linear constraints to the matrix form A*x and Aeq*x = beq . In other words, get the x variables on the left-hand side of the expressions, and make the inequality into less than or equal form:

Set bounds lb and ub .

Solve the constrained problem using ga .

Check that the linear constraints are satisfied to within the default value of ConstraintTolerance , 1e-3 .

Optimize with Nonlinear Constraints Using ga

Use the genetic algorithm to minimize the ps_example function on the region 2 x 1 2 + x 2 2 ≤ 3 and ( x 1 + 1 ) 2 = ( x 2 / 2 ) 4 .

To do so, first write a function ellipsecons.m that returns the inequality constraint in the first output, c , and the equality constraint in the second output, ceq . Save the file ellipsecons.m to a folder on your MATLAB® path.

Include a function handle to ellipsecons as the nonlcon argument.

Check that the nonlinear constraints are satisfied at x . The constraints are satisfied when c ≤ 0 and ceq = 0 to within the default value of ConstraintTolerance , 1e-3 .

Minimize with Nondefault Options

Use the genetic algorithm to minimize the ps_example function on the region x(1) + x(2) >= 1 and x(2) == 5 + x(1) using a constraint tolerance that is smaller than the default.

First, convert the two constraints to the matrix form A*x and Aeq*x = beq . In other words, get the x variables on the left-hand side of the expressions, and make the inequality into less than or equal form:

To obtain a more accurate solution, set a constraint tolerance of 1e-6 . And to monitor the solver progress, set a plot function.

Solve the minimization problem.

Check that the linear constraints are satisfied to within 1e-6 .

Minimize a Nonlinear Function with Integer Constraints

Use the genetic algorithm to minimize the ps_example function subject to the constraint that x(1) is an integer.

Obtain the Solution and Function Value

Use to genetic algorithm to minimize an integer-constrained nonlinear problem. Obtain both the location of the minimum and the minimum function value.

Compare this result to the solution of the problem with no constraints.

Obtain Diagnostic Information

Use the genetic algorithm to minimize the ps_example function constrained to have x(1) integer-valued. To understand the reason the solver stopped and how ga searched for a minimum, obtain the exitflag and output results. Also, plot the minimum observed objective function value as the solver progresses.

Obtain Final Population and Scores

Use the genetic algorithm to minimize the ps_example function constrained to have x(1) integer-valued. Obtain all outputs, including the final population and vector of scores.

Examine the first 10 members of the final population and their corresponding scores. Notice that x(1) is integer-valued for all these population members. The integer ga algorithm generates only integer-feasible populations.

Видео:How to solve Genetic Algorithm by using MATLABСкачать

Input Arguments

fun — Objective function
function handle | function name

Objective function, specified as a function handle or function name. Write the objective function to accept a row vector of length nvars and return a scalar value.

When the ‘UseVectorized’ option is true , write fun to accept a pop -by- nvars matrix, where pop is the current population size. In this case, fun returns a vector the same length as pop containing the fitness function values. Ensure that fun does not assume any particular size for pop , since ga can pass a single member of a population even in a vectorized calculation.

Example: fun = @(x)(x-[4,2]).^2

Data Types: char | function_handle | string

nvars — Number of variables
positive integer

Number of variables, specified as a positive integer. The solver passes row vectors of length nvars to fun .

Example: 4

Data Types: double

A — Linear inequality constraints
real matrix

Linear inequality constraints, specified as a real matrix. A is an M -by- nvars matrix, where M is the number of inequalities.

A encodes the M linear inequalities

where x is the column vector of nvars variables x(:) , and b is a column vector with M elements.

For example, to specify

give these constraints:

Example: To specify that the control variables sum to 1 or less, give the constraints A = ones(1,N) and b = 1 .

Data Types: double

b — Linear inequality constraints
real vector

Linear inequality constraints, specified as a real vector. b is an M -element vector related to the A matrix. If you pass b as a row vector, solvers internally convert b to the column vector b(:) .

b encodes the M linear inequalities

where x is the column vector of N variables x(:) , and A is a matrix of size M -by- N .

For example, to specify

give these constraints:

Example: To specify that the control variables sum to 1 or less, give the constraints A = ones(1,N) and b = 1 .

Data Types: double

Aeq — Linear equality constraints
real matrix

Linear equality constraints, specified as a real matrix. Aeq is an Me -by- nvars matrix, where Me is the number of equalities.

Aeq encodes the Me linear equalities

where x is the column vector of N variables x(:) , and beq is a column vector with Me elements.

For example, to specify

give these constraints:

Example: To specify that the control variables sum to 1, give the constraints Aeq = ones(1,N) and beq = 1 .

Data Types: double

beq — Linear equality constraints
real vector

Linear equality constraints, specified as a real vector. beq is an Me -element vector related to the Aeq matrix. If you pass beq as a row vector, solvers internally convert beq to the column vector beq(:) .

beq encodes the Me linear equalities

where x is the column vector of N variables x(:) , and Aeq is a matrix of size Meq -by- N .

For example, to specify

give these constraints:

Example: To specify that the control variables sum to 1, give the constraints Aeq = ones(1,N) and beq = 1 .

Data Types: double

lb — Lower bounds
[] (default) | real vector or array

Lower bounds, specified as a real vector or array of doubles. lb represents the lower bounds element-wise in lb ≤ x ≤ ub .

Internally, ga converts an array lb to the vector lb(:) .

Example: lb = [0;-Inf;4] means x(1) ≥ 0 , x(3) ≥ 4 .

Data Types: double

ub — Upper bounds
[] (default) | real vector or array

Upper bounds, specified as a real vector or array of doubles. ub represents the upper bounds element-wise in lb ≤ x ≤ ub .

Internally, ga converts an array ub to the vector ub(:) .

Example: ub = [Inf;4;10] means x(2) ≤ 4 , x(3) ≤ 10 .

Data Types: double

nonlcon — Nonlinear constraints
function handle | function name

Nonlinear constraints, specified as a function handle or function name. nonlcon is a function that accepts a vector or array x and returns two arrays, c(x) and ceq(x) .

c(x) is the array of nonlinear inequality constraints at x . ga attempts to satisfy

for all entries of c .

ceq(x) is the array of nonlinear equality constraints at x . ga attempts to satisfy

for all entries of ceq .

where mycon is a MATLAB ® function such as

To learn how to use vectorized constraints, see Vectorized Constraints.

Note

ga does not enforce nonlinear constraints to be satisfied when the PopulationType option is set to ‘bitString’ or ‘custom’ .

If intcon is not empty, the second output of nonlcon ( ceq ) must be an empty entry ( [] ).

For information on how ga uses nonlcon , see Nonlinear Constraint Solver Algorithms.

Data Types: char | function_handle | string

options — Optimization options
output of optimoptions | structure

Optimization options, specified as the output of optimoptions or a structure.

optimoptions hides the options listed in italics . See Options that optimoptions Hides.

Values in denote the default value.

* represents the default when there are linear constraints, and for MutationFcn also when there are bounds.

I* indicates default for integer constraints, or indicates special considerations for integer constraints.

NM indicates that the option does not apply to gamultiobj .

Options for ga and gamultiobj

Determines the feasibility with respect to nonlinear constraints. Also, max(sqrt(eps),ConstraintTolerance) determines feasibility with respect to linear constraints.

For an options structure, use TolCon .

Function that creates the initial population. Specify as a name of a built-in creation function or a function handle. See Population Options.

Function that the algorithm uses to create crossover children. Specify as a name of a built-in crossover function or a function handle. See Crossover Options.

for ga , * for gamultiobj | I* | ‘crossoverheuristic’ | ‘crossoversinglepoint’ | ‘crossovertwopoint’ | ‘crossoverarithmetic’ | Custom crossover function

The fraction of the population at the next generation, not including elite children, that the crossover function creates.

Level of display.

‘off’ | ‘iter’ | ‘diagnose’ |

Function that computes the distance measure of individuals. Specify as a name of a built-in distance measure function or a function handle. The value applies to the decision variable or design space (genotype) or to function space (phenotype). The default ‘distancecrowding’ is in function space (phenotype). For gamultiobj only. See Multiobjective Options.

For an options structure, use a function handle, not a name.

NM Positive integer specifying how many individuals in the current generation are guaranteed to survive to the next generation. Not used in gamultiobj .

NM If the fitness function attains the value of FitnessLimit , the algorithm halts.

Function that scales the values of the fitness function. Specify as a name of a built-in scaling function or a function handle. Option unavailable for gamultiobj .

The algorithm stops if the average relative change in the best fitness function value over MaxStallGenerations generations is less than or equal to FunctionTolerance . If StallTest is ‘geometricWeighted’ , then the algorithm stops if the weighted average relative change is less than or equal to FunctionTolerance .

For gamultiobj , the algorithm stops when the geometric average of the relative change in value of the spread over options.MaxStallGenerations generations is less than options.FunctionTolerance , and the final spread is less than the mean spread over the past options.MaxStallGenerations generations. See gamultiobj Algorithm.

For an options structure, use TolFun .

Positive scalar | for ga , for gamultiobj

I* Function that continues the optimization after ga terminates. Specify as a name or a function handle.

Alternatively, a cell array specifying the hybrid function and its options. See ga Hybrid Function.

For gamultiobj , the only hybrid function is @fgoalattain . See gamultiobj Hybrid Function.

When the problem has integer constraints, you cannot use a hybrid function.

Function name or handle | ‘fminsearch’ | ‘patternsearch’ | ‘fminunc’ | ‘fmincon’ |

1-by-2 cell array | , where solver = fminsearch , patternsearch , fminunc , or fmincon

NM I* Initial value of the penalty parameter

Initial population used to seed the genetic algorithm. Has up to PopulationSize rows and N columns, where N is the number of variables. You can pass a partial population, meaning one with fewer than PopulationSize rows. In that case, the genetic algorithm uses CreationFcn to generate the remaining population members. See Population Options.

For an options structure, use InitialPopulation .

Matrix or vector specifying the range of the individuals in the initial population. Applies to gacreationuniform creation function. ga shifts and scales the default initial range to match any finite bounds.

For an options structure, use PopInitRange .

Matrix or vector | for unbounded components, for unbounded components of integer-constrained problems, for bounded components, with the default range modified to match one-sided bounds

Initial scores used to determine fitness. Has up to PopulationSize rows and Nf columns, where Nf is the number of fitness functions ( 1 for ga , greater than 1 for gamultiobj ). You can pass a partial scores matrix, meaning one with fewer than PopulationSize rows. In that case, the solver fills in the scores when it evaluates the fitness functions.

For an options structure, use InitialScores .

Column vector for single objective | matrix for multiobjective |

Maximum number of iterations before the algorithm halts.

For an options structure, use Generations .

The algorithm stops if the average relative change in the best fitness function value over MaxStallGenerations generations is less than or equal to FunctionTolerance . If StallTest is ‘geometricWeighted’ , then the algorithm stops if the weighted average relative change is less than or equal to FunctionTolerance .

For gamultiobj , the algorithm stops when the geometric average of the relative change in value of the spread over options.MaxStallGenerations generations is less than options.FunctionTolerance , and the final spread is less than the mean spread over the past options.MaxStallGenerations generations. See gamultiobj Algorithm.

For an options structure, use StallGenLimit .

Positive integer | for ga , for gamultiobj

NM The algorithm stops if there is no improvement in the objective function for MaxStallTime seconds, as measured by tic and toc .

For an options structure, use StallTimeLimit .

The algorithm stops after running for MaxTime seconds, as measured by tic and toc . This limit is enforced after each iteration, so ga can exceed the limit when an iteration takes substantial time.

For an options structure, use TimeLimit .

Direction of migration. See Migration Options.

Scalar from 0 through 1 specifying the fraction of individuals in each subpopulation that migrates to a different subpopulation. See Migration Options.

Positive integer specifying the number of generations that take place between migrations of individuals between subpopulations. See Migration Options.

Function that produces mutation children. Specify as a name of a built-in mutation function or a function handle. See Mutation Options.

for ga without constraints | * for gamultiobj and for ga with constraints | I* | ‘mutationpositivebasis’ | ‘mutationuniform’ | Custom mutation function

Nonlinear constraint algorithm. See Nonlinear Constraint Solver Algorithms. Option unchangeable for gamultiobj .

For an options structure, use NonlinConAlgorithm .

Functions that ga calls at each iteration. Specify as a function handle or a cell array of function handles. See Output Function Options.

For an options structure, use OutputFcns .

Function handle or cell array of function handles |

Scalar from 0 through 1 specifying the fraction of individuals to keep on the first Pareto front while the solver selects individuals from higher fronts, for gamultiobj only. See Multiobjective Options.

NM I* Penalty update parameter.

Function that plots data computed by the algorithm. Specify as a name of a built-in plot function, a function handle, or a cell array of built-in names or function handles. See Plot Options.

For an options structure, use PlotFcns .

ga or gamultiobj : | ‘gaplotdistance’ | ‘gaplotgenealogy’ | ‘gaplotselection’ | ‘gaplotscorediversity’ |’gaplotscores’ | ‘gaplotstopping’ | ‘gaplotmaxconstr’ | Custom plot function

ga only: ‘gaplotbestf’ | ‘gaplotbestindiv’ | ‘gaplotexpectation’ | ‘gaplotrange’

gamultiobj only: ‘gaplotpareto’ | ‘gaplotparetodistance’ | ‘gaplotrankhist’ | ‘gaplotspread’

Positive integer specifying the number of generations between consecutive calls to the plot functions.

Size of the population.

Positive integer | when numberOfVariables , otherwise | for mixed-integer problems

Data type of the population. Must be ‘doubleVector’ for mixed-integer problems.

ga ignores all constraints when PopulationType is set to ‘bitString’ or ‘custom’ . See Population Options.

Function that selects parents of crossover and mutation children. Specify as a name of a built-in selection function or a function handle.

gamultiobj uses only ‘selectiontournament’ .

for ga , for gamultiobj | ‘selectionremainder’ | ‘selectionuniform’ | ‘selectionroulette’ | Custom selection function

NM Stopping test type.

For an options structure, use Vectorized with the values ‘on’ or ‘off’ .

Example: optimoptions(‘ga’,’PlotFcn’,@gaplotbestf)

intcon — Integer variables
vector of positive integers

Integer variables, specified as a vector of positive integers taking values from 1 to nvars . Each value in intcon represents an x component that is integer-valued.

Note

When intcon is nonempty, nonlcon must return empty for ceq . For more information on integer programming, see Mixed Integer ga Optimization.

Example: To specify that the even entries in x are integer-valued, set intcon to 2:2:nvars

Data Types: double

problem — Problem description
structure

Problem description, specified as a structure containing these fields.

Number of design variables

A matrix for linear inequality constraints

b vector for linear inequality constraints

Aeq matrix for linear equality constraints

beq vector for linear equality constraints

Lower bound on x

Upper bound on x

Nonlinear constraint functions

Field to reset the state of the random number generator

Options created using optimoptions or an options structure

You must specify the fields fitnessfcn , nvars , and options . The remainder are optional for ga .

📹 Видео

Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

Значение Янтр и Мандал: Влияние и Различия в Магической ПрактикеСкачать

#9. Пример поиска минимума функции | Генетические алгоритмы на PythonСкачать

What is a Genetic AlgorithmСкачать

Многокритериальная оптимизация в MATLABСкачать

GMP – 3. Основы MATLAB SimulinkСкачать

Двухцелевой генетический алгоритм в Matlab (часть 2)Скачать

Двухцелевой генетический алгоритм в Matlab (часть 1)Скачать

Создаём мозг для "змейки". Часть1.Скачать

Алгоритм симуляции отжига в MATLAB. Global Optimization ToolboxСкачать

Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать