Где используются тригонометрические уравнения в жизни

Данная тема является одной из самых актуальных. Она находит широкое применение в разных разделах математики, и других областях науки, а также тесно связана с деятельностью человека. Имеет теоретическую и практическую значимость.

Объект исследования: Тригонометрия.

Предмет исследования: Графики тригонометрической функции – синусоида и косинусоида.

Узнать о способах применения графиков тригонометрических функции в жизни человека.

Составить историческую справку о графиках тригонометрических функций.

Описать применении графиков тригонометрических функций в окружающем нас мире и различных отраслях.

Вывести свой биоритм жизни.

Изготовить демонстрационную модель движения графика синуса.

Графики тригонометрических функций широко применяются человеком, начиная с древности, и заканчивая настоящим временем.

Многие задаются вопросами: зачем нужна тригонометрия? Как она используется в нашем мире? С чем может быть связана тригонометрия? И вот ответы на эти вопросы.

Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов), когда требуется сферическая тригонометрия, в акустике, в оптике, в анализе финансовых рынков, в статистике, в биологии, в медицинской визуализации, например, компьютерной томографии и ультразвук, в химии (Приложение 1, рис.1), в сейсмологии (Приложение 1, рис.2), в метеорологии, в океанографии (Приложение 1, рис.3), в архитектуре (Приложение 1, рис.4), в экономике, в компьютерной графике, в кристаллографии (Приложение 1, рис.5) и многих других областях.

Часто с синусами и косинусами приходится сталкиваться геодезистам. Они имеют специальные инструменты для точного измерения углов. При помощи синусов и косинусов углы можно превратить в длины или координаты точек на земной поверхности.

Зачатки тригонометрии можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая (Приложение 2, рис.1) . 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.

Дальнейшее развитие тригонометрии связано с именем астронома Аристарха Самосского (III век до н. э.). В его трактате «О величинах и расстояниях Солнца и Луны» ставилась задача об определении расстояний до небесных тел; эта задача требовала вычисления отношения сторон прямоугольного треугольника при известном значении одного из углов. Аристарх рассматривал прямоугольный треугольник, образованный Солнцем, Луной и Землёй во время квадратуры (Приложение 2, рис. 2). Ему требовалось вычислить величину гипотенузы (расстояние от Земли до Солнца) через катет (расстояние от Земли до Луны) при известном значении прилежащего угла (87°), что эквивалентно вычислению значения sin угла 3. По оценке Аристарха, эта величина лежит в промежутке от 1/20 до 1/18, то есть расстояние до Солнца в 20 раз больше, чем до Луны; на самом деле Солнце почти в 400 раз дальше, чем Луна, ошибка возникла из-за неточности в измерении угла.

Несколько десятилетий спустя Клавдий Птоломей в своих трудах «География», «Аналемма» и «Планисферий» даёт подробное изложение тригонометрических приложений к картографии, астрономии и механике. Среди прочего, описана стереографическая проекция, исследованы несколько практических задач, например: определить высоту и азимут небесного светила по его склонению и часовому углу. С точки зрения тригонометрии, это значит, что надо найти сторону сферического треугольника по другим двум сторонам и противолежащему углу.

В общем, можно сказать, что тригонометрия использовалась для:

· точного определения времени суток; (Приложение 2, рис. 3)

· вычисления будущего расположения небесных светил, моментов их восхода и заката, затмений Солнца и Луны;

· нахождения географических координат текущего места;

· вычисления расстояния между городами с известными географическими координатами.

Гномон— древнейший астрономический инструмент, вертикальный предмет (стела, колонна, шест), позволяющий по наименьшей длине его тени (в полдень)

определить угловую высоту солнца. Так, под котангенсом понималась длина тени от вертикального гномонавысотой 12 (иногда 7) единиц; первоначально эти понятия использовались для расчёта солнечных часов. Тангенсом называлась тень от горизонтального гномона. Косекансом и секансом назывались гипотенузы соответствующих прямоугольных треугольников (отрезки AO на рисунке слева)

Тригонометри́ческие фу́нкции (Приложение 2, рис. 5) — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла (дуги) в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.

Синус и косинус относятся к прямым тригонометрическим функциям.

Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива», то есть половина хорды данной дуги, поскольку дуга с хордой напоминает лук с тетивой). Затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские математики, переводя индийские книги с санскрита, не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали его арабскими буквами и стали называть линию синуса «джиба» ( جيب‎ ). Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса как «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus — «синус», имеющим то же значение (следует отметить, что именно в этом значении оно применяется как анатомический термин синус). Термин «косинус» (лат. Cosinus) — это сокращение от лат. Complementi sinus — дополнительный синус.

Первый график синусоиды (Приложение 2, рис. 6) появился в книге Альбрехта Дюрера (Приложение 2, рис. 4) «Руководство к измерению циркулем и линейкой» (нем. Underweysung der Messung mit dem Zirkel und Richtscheyt, 1525 год). В 1630-х годах, Жиль Роберваль (Приложение 2, рис. 7), в ходе своих исследований циклоиды, независимо вычертил синусоиду, он же опубликовал формулу тангенса двойного угла. Джон Валлис (Приложение 2, рис. 8) в своей «Механике» (1670), опередив своё время, правильно указал знаки синуса во всех квадрантах и указал, что у синусоиды бесконечно много «оборотов». График тангенса для первого квадранта впервые начертил Джеймс Грегори (1668) (Приложение 2, рис. 9).

В настоящее время график синуса можно встретить в следующих моментах нашей жизни.

Широко используется тригонометрия в строительстве, а особенно в архитектуре. Большинство композиционных решений и построений

рисунков проходило именно с помощью геометрии. Но теоретические данные мало что значат. Хочу привести пример на построение одной скульптуры французского мастера Золотого века искусства.

Пропорциональное соотношение в построении статуи было идеально. Однако при поднятии статуи на высокий пьедестал, она смотрелась уродливой.

Скульптором не было учтено, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности. Велось множество расчетов, чтобы фигура с большой высоты смотрелась пропорционально. В основном они были основаны на методе визирования, то есть приблизительного измерения, на глаз. Однако коэффициент разности тех или иных пропорций позволили сделать фигуру более приближенной к идеалу. Таким образом, зная примерное расстояние от статуи до точки зрения, а именно от верха статуи до глаз человека и высоту статуи, можно рассчитать синус угла падения взгляда с помощью таблицы (то же самое мы можем сделать и с нижней точкой зрения), тем самым найдем точку зрения

Ситуация меняется, так как статую поднимают на высоту, поэтому расстояние от верхушки статуи до глаз человека увеличивается, следовательно и синус угла падения увеличивается. Сравнив изменения расстояния от верхушки статуи до земли в первом и во втором случаи, можно найти коэффициент пропорциональности. Впоследствии мы получим чертеж, а потом скульптуру, при поднятии которой зрительно фигура будет приближена к идеалу.

Медицина и биология.

Модель биоритмов (Приложение 2, рис.11), которые в свою очередь подразумевают цикличность процессов в живом организме можно построить с помощью тригонометрических функций. Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).

Формула сердца. В результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси, медики впервые получили возможность упорядочить информацию, относящуюся к электрической активности сердца или, другими словами, электрокардиографии.

Формула представляет собой комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики, эта формула в значительной степени облегчает процесс описания основных параметров, деятельности сердца, ускоряя, тем самым, постановку диагноза и начало собственно лечения.

Также тригонометрия помогает нашему мозгу определять расстояния до объектов.

Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. Строго говоря, идея «измерения углов» не является новой. Еще художники Древнего Китая рисовали удаленные объекты выше в поле зрения, несколько пренебрегая законами перспективы. Сформулировал теорию определения расстояния по оценке углов арабский ученый XI века Альхазен. После долгого забвения в середине прошлого столетия идею реанимировал психолог Джеймс Гибсон (James Gibson), строивший свои выводы на основе опыта работы с пилотами военной авиации. Однако после того о теории вновь позабыли.

Движение рыб в воде и полёт птиц (Приложение 2, рис. 10) происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.

Тригонометрией пользуются при измерение расстояния между точек на местности. Предположим, что нам надо найти расстояние d от пункта А до недоступного пункта «дерево». На местности можно выбрать точку B и измерим длину с отрезка АВ. Затем измерим, например с помощью астролябии, углы A и B. Эти данные, т.е. c, a и b позволяют решить треугольник АВС и найти искомое расстояние d = AC. Сначала находим угол С sinC: С=180-а- b , sinC = sin (180- a — b )= sin ( a + b ). Затем с помощью теоремы синусов находим d.

Изготовление демонстрационной модели движения графика синуса.

Для изготовления данной модели мне потребовалось:

Изготовление модели мы начали с того, что:

Вырезали фанеру по нужному размеру.

Нанесли на неё разметку в виде графика синуса и косинуса на координатной плоскости.

Панель покрыли мебельным лаком.

По контуру синусоиды разместили силовые кнопки.

По силовым кнопкам протянули шляпную резинку с обозначением начальной точки.

Испытали модель в действии.

Описание аналитической части.

Изучив графики тригонометрических функций – синусоиду и косинусоиду, можно сделать вывод, что тригонометрия тесно связана с жизнью человека и его деятельностью, начиная с древности, и заканчивая настоящим временем.

Исследовав аналитический материал, мы выяснили, что тригонометрия присутствует во многих областях науки.

Дали строгие определения тригонометрии и тригонометрическим функциям.

Определили сферы применения синусоиды и косинусоиды, а также подтвердили значимость математики в окружающем нас мире. В ходе практического исследования применили полученные знания..

Мы убедились, что выдвинутая нами гипотеза подтвердилась и графики тригонометрических функций – синусоида и косинусоида действительно являются яркими представительницами в окружающем нас мире, а не только линиями в тетради. Они являются замечательными кривыми, которые практически всегда рядом с нами.

Хочется, чтобы данное исследование оказалось не только интересным, но и полезным. А демонстрационная модель будет служить наглядностью на уроках математики при изучении этих функций. Имеет метапредметную связь с другими областями науки.

Видео:СУТЬ ТРИГОНОМЕТРИИСкачать

Где используются тригонометрические уравнения в жизни

Видео:ЗАЧЕМ НУЖНА ЭТА ... тригонометрия! Математика на QWERTYСкачать

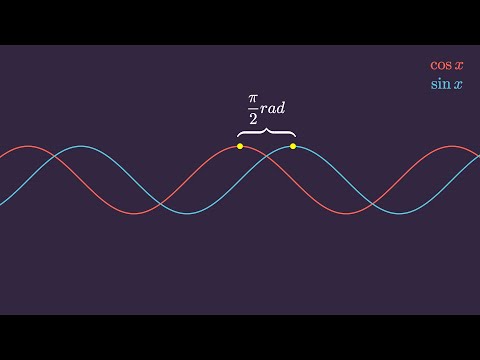
Тригонометрия

Тригонометрия в жизни

ТРИГОНОМЕТРИЯ В НАШЕЙ ЖИЗНИ

Многие задаются вопросами: зачем нужна тригонометрия? Как она используется в нашем мире? С чем может быть связана тригонометрия? И вот ответы на эти вопросы. Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов), когда требуется сферическая тригонометрия, в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятности, в статистике, в биологии, в медицинской визуализации ,например, компьютерной томографии и ультразвук, в аптеках, в химии, в теории чисел, в сейсмологии, в метеорологии, в океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях.

Часто с синусами и косинусами приходится сталкиваться геодезистам. Они имеют специальные инструменты для точного измерения углов. При помощи синусов и косинусов углы можно превратить в длины или координаты точек на земной поверхности.

Зачатки тригонометрии можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая. 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.

Несколько десятилетий спустя Клавдий Птоломей в своих трудах «География», «Аналемма» и «Планисферий» даёт подробное изложение тригонометрических приложений к картографии, астрономии и механике. Среди прочего, описана стереографическая проекция, исследованы несколько практических задач, например: определить высоту и азимут небесного светила по его склонению и часовому углу. С точки зрения тригонометрии, это значит, что надо найти сторону сферического треугольника по другим двум сторонам и противолежащему углу.

· точного определения времени суток;

· вычисления будущего расположения небесных светил, моментов их восхода и заката, затмений Солнца и Луны ;

· нахождения географических координат текущего места;

· вычисления расстояния между городами с известными географическими координатами.

Гномон— древнейший астрономический инструмент, вертикальный предмет (стела, колонна, шест),

Так, под котангенсом понималась длина тени от вертикального гномонавысотой 12 (иногда 7) единиц; первоначально эти понятия использовались для расчёта солнечных часов. Тангенсом называлась тень от горизонтального гномона. Косекансом и секансом назывались гипотенузы соответствующих прямоугольных треугольников (отрезки AO на рисунке слева)

Широко используется тригонометрия в строительстве, а особенно в архитектуре. Большинство композиционных решений и построений

Пропорциональное соотношение в построении статуи было идеально. Однако при поднятии статуи на высокий пьедестал, она смотрелась уродливой. Скульптором не было учтено, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности. Велось

Ситуация меняется , так как статую поднимают на высоту, поэтому расстояние от верхушки статуи до глаз человека увеличивается, следовательно и синус угла падения увеличивается. Сравнив изменения расстояния от верхушки статуи до земли в первом и во втором случаи, можно найти коэффициент пропорциональности. Впоследствии мы получим чертеж, а потом скульптуру, при поднятии которой зрительно фигура будет приближена к идеалу

Модель боритмов можно построить с помощью тригонометрических функций. Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).

Формула сердца. В результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси, медики впервые получили возможность упорядочить информацию, относящуюся к электрической активности сердца или, другими словами, электрокардиографии. Формула представляет собой комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики, эта формула в значительной степени облегчает процесс описания основных параметров деятельности сердца, ускоряя, тем самым, постановку диагноза и начало собственно лечения.

Также тригонометрия помогает нашему мозгу определять расстояния до объектов.

Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. Строго говоря, идея «измерения углов» не является новой. Еще художники Древнего Китая рисовали удаленные объекты выше в поле зрения, несколько пренебрегая законами перспективы. Сформулировал теорию определения расстояния по оценке углов арабский ученый XI века Альхазен. После долгого забвения в середине прошлого столетия идею реанимировал психолог Джеймс

Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму

d B и измерим длину с отрезка АВ. Затем измерим, например

с помощью астролябии, углы A и B . Эти данные, т.е. c , a и b

позволяют решить треугольник АВС и найти искомое

С =180- а -b, sinC=sin(180-a-b)=sin(a+b)

Затем с помощью теоремы синусов находим d .

Видео:Зачем нужна тригонометрия в жизниСкачать

Курсовая работа » Использование тригонометрии в жизни»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Муниципальное образовательное учреждение лицей №86

Использование тригонометрии в жизни

Курсовая работа

Автор–Светлов Владислав,

МОУ лицей №86 г.Ярославль

Арабаджи Елена Владимировна

История тригонометрии………………………………………. стр. 4

Тригонометрические уравнения………………………………. стр. 8

Схема решения тригонометрических уравнений……………. стр. 9

Способы решения тригонометрических уравнений…………..стр. 11

Практическое применение тригонометрии…………………. стр. 12

Тригонометрия в биологии……………………………………..стр. 13

Тригонометрия в медицине……………………………………..стр. 14

Тригонометрия в физике………………………………….……стр. 16

Тригонометрия в природе………………………………………стр. 17

Тригонометрия в музыке………………………………………..стр.17

Тригонометрия помогает мозгу………………………………. стр. 18

Тригонометрия в архитектуре………………………………. стр. 18

ИСПОЛЬЗОВАНИЕ ТРИГОНОМЕТРИИ В ЖИЗНИ.

Тригонометрия — это раздел математики, в котором изучаются зависимости между величинами углов и длинами сторон треугольников, а также алгебраические тождества тригонометрических функций. С этой наукой мы сталкиваемся не только на уроках математики, но и в нашей повседневной жизни. Тригонометрия встречается в таких науках, как физика, биология, не последнюю роль она играет и в медицине, и, что самое интересное, без нее не обошлось даже в музыке и архитектуре. Значительную роль играют задачи с практическим содержанием. Каждого изучающего математику, интересует как и где применяются полученные знания. Ответ на этот вопрос и дает данная работа. Я считаю, что большинство физических явлений природы, физиологических процессов, закономерностей в музыке и искусстве можно описать с помощью тригонометрии и тригонометрических функций. По звездам вычисляли местонахождение корабля в море. Древние люди вычисляли высоту дерева, сравнивая длину его тени с длиной тени от шеста, высота которого была известна. Тригонометрия (от греч. trigwnon — треугольник и metrew — измеряю).

Узнать где и как используется тригонометрия в окружающем нас мире.

Изучить историю тригонометрии

Узнать где используется тригонометрия

Узнать как используется тригонометрия в других науках

Сделать вывод о проделанной работе

Видео:История создания синуса и косинуса (Алгебра, 10)Скачать

Общие сведения о тригонометрии

История тригонометрии началась более двух тысячелетий назад. Первоначально ее возникновение было связано с необходимостью выяснения соотношений углов и сторон треугольника. В процессе исследований выяснилось, что математическое выражение данных соотношений требует введения особых тригонометрических функций, которые первоначально оформлялись как числовые таблицы.

Для многих смежных с математикой наук толчком к развитию стала именно история тригонометрии. Происхождение единиц измерения углов (градусов), связанное с исследованиями ученых Древнего Вавилона, опирается на шестидесятиричную систему исчисления, которая дала начала современной десятиричной, применяемой во многих прикладных науках.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Тригонометрия в ранние века

Руководствуясь данными о сохранившихся научных реликвиях, исследователи сделали вывод, что история возникновения тригонометрии связана с работами греческого астронома Гиппарха, который впервые задумался над поиском способов решения треугольников (сферических). Его труды относятся ко 2 веку до нашей эры.

Также одним из важнейших достижений тех времен является определение соотношения катетов и гипотенузы в прямоугольных треугольниках, которое позже получило название теоремы Пифагора.

История развития тригонометрии в Древней Греции связана с именем астронома Птоломея — автора геоцентрической системы мира, господствовавшей до Коперника.

Греческим астрономам не были известны синусы, косинусы и тангенсы. Они пользовались таблицами, позволяющими найти значение хорды окружности с помощью стягиваемой дуги. Единицами для измерения хорды были градусы, минуты и секунды. Один градус приравнивался к шестидесятой части радиуса.

Также исследования древних греков продвинули развитие сферической тригонометрии. В частности, Евклид в своих «Началах» приводит теорему о закономерностях соотношений объемов шаров различного диаметра. Его труды в этой области стали своеобразным толчком в развитии еще и смежных областей знаний. Это, в частности, технология астрономических приборов, теория картографических проекций, система небесных координат и т. д.

Видео:Задача, в которой школьники усложняют себе жизнь на ЕГЭ. Зачем нужна тригонометрияСкачать

Средневековье: исследования индийских ученых

Значительных успехов достигли индийские средневековые астрономы. Гибель античной науки в IV веке обусловила перемещение центра развития математики в Индию.

История возникновения тригонометрии как обособленного раздела математического учения началась в Средневековье. Именно тогда ученые заменили хорды синусами. Это открытие позволило ввести функции, касающиеся исследования сторон и углов прямоугольного треугольника. То есть именно тогда тригонометрия начала обосабливаться от астрономии, превращаясь в раздел математики.

Первые таблицы синусов были у Ариабхаты, они была проведены через 3 о , 4 о , 5 о . Позже появились подробные варианты таблиц: в частности, Бхаскара привел таблицу синусов через 1 о .

Первый специализированный трактат по тригонометрии появился в X—XI веке. Автором его был среднеазиатский учёный Аль-Бируни. А в своем главном труде «Канон Мас‘уда» (книга III) средневековый автор еще более углубляется в тригонометрию, приводя таблицу синусов (с шагом 15′) и таблицу тангенсов (с шагом 1°).

Видео:тригонометрия в реальной жизниСкачать

История развития тригонометрии в Европе

После перевода арабских трактатов на латынь (XII-XIII в) большинство идей индийских и персидских ученых были заимствованы европейской наукой. Первые упоминания о тригонометрии в Европе относятся к XII веку.

По мнению исследователей, история тригонометрии в Европе связана с именем англичанина Ричарда Уоллингфордского, который стал автором сочинения «Четыре трактата о прямых и обращенных хордах». Именно его труд стал первой работой, которая целиком посвящена тригонометрии. К XV веку многие авторы в своих трудах упоминают о тригонометрических функциях.

Видео:Математика это не ИсламСкачать

История тригонометрии: Новое время

В Новое время большинство ученых стало осознавать чрезвычайную важность тригонометрии не только в астрономии и астрологии, но и в других областях жизни. Это, в первую очередь, артиллерия, оптика и навигация в дальних морских походах. Поэтому во второй половине XVI века эта тема заинтересовала многих выдающихся людей того времени, в том числе Николая Коперника, Иоганна Кеплера, Франсуа Виета. Коперник отвел тригонометрии несколько глав своего трактата «О вращении небесных сфер» (1543). Чуть позже, в 60-х годах XVI века, Ретик — ученик Коперника — приводит в своем труде «Оптическая часть астрономии» пятнадцатизначные тригонометрические таблицы.

Франсуа Виет в «Математическом каноне» (1579) дает обстоятельную и систематическую, хотя и бездоказательную, характеристику плоской и сферической тригонометрии. А Альбрехт Дюрер стал тем, благодаря кому на свет появилась синусоида.

Видео:Тригонометрия в ЕГЭ может быть простойСкачать

Заслуги Леонарда Эйлера

Придание тригонометрии современного содержания и вида стало заслугой Леонарда Эйлера. Его трактат «Введение в анализ бесконечных» (1748) содержит определение термина «тригонометрические функции», которое эквивалентно современному. Таким образом, этот ученый смог определить обратные функции. Но и это еще не все.

Определение тригонометрических функций на всей числовой прямой стало возможным благодаря исследованиям Эйлера не только допустимых отрицательных углов, но и углов боле 360°. Именно он в своих работах впервые доказал, что косинус и тангенс прямого угла отрицательные. Разложение целых степеней косинуса и синуса тоже стало заслугой этого ученого. Общая теория тригонометрических рядов и изучение сходимости полученных рядов не были объектами исследований Эйлера. Однако, работая над решением смежных задач, он сделал много открытий в этой области. Именно благодаря его работам продолжилась история тригонометрии. Кратко в своих трудах он касался и вопросов сферической тригонометрии.

Видео:Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать

История происхождения основных понятий

История возникновения и развития тригонометрии насчитывает не один век. Введение понятий, которые составляют основу этого раздела математической науки, также не было одномоментным.

Так, понятие «синус» имеет очень долгую историю. Упоминания о различных отношениях отрезков треугольников и окружностей обнаруживаются еще в научных трудах, датируемых III веком до нашей эры. Работы таких великих древних ученых, как Евклид, Архимед, Апполоний Пергский, уже содержат первые исследования этих соотношений. Новые открытия требовали определенных терминологических уточнений. Так, индийский учёный Ариабхата дает хорде название «джива», означающее «тетива лука». Когда арабские математические тексты переводились на латынь, термин заменили близким по значению синусом (т. е. «изгиб»).

Слово «косинус» появилось намного позже. Этот термин является сокращенным вариантом латинской фразы «дополнительный синус».

Возникновение тангенсов связано с расшифровкой задачи определения длины тени. Термин «тангенс» ввел в X веке арабский математик Абу-ль-Вафа, составивший первые таблицы для определения тангенсов и котангенсов. Но европейские ученые не знали об этих достижениях. Немецкий математик и астроном Регимонтан заново открывает эти понятия в 1467 г. Доказательство теоремы тангенсов – его заслуга. А переводится этот термин как «касающийся».

Простейшие тригонометрические уравнения

Простейшие тригонометрические уравнения — это уравнения вида f ( kx + b )= a , где f ( x ) — одна из тригонометрических функций: sinx , cosx , tgx . Элементарные тригонометрические уравнения имеют бесконечно много корней. Например, уравнению sinx =1/2 удовлетворяют следующие значения: x ₁ =π/6, x ₂ =5π/6, x ₃ =π/6+2π, x ₄ =π/6-2πи т. д. Общая формула по которой находятся все корни уравнения sin ( x )= a , где │ a │≤1, такова: x =(-1) k arcsin ( a +π n )

Здесь n может принимать любые целые значения, каждому из них соответствует определенный корень уравнения; в этой формуле (равно как и в других формулах, по которым решаются элементарные тригонометрические уравнения) n называют параметром . Записывают обычно nϵZ , подчеркивая тем самым, что параметр n принимать любые целые значения.

Решения уравнения cos ( x ), где │ a │≤1, находятся по формуле x = ± arcsin ( a +2π n ), nϵZ

Особо отмечу некоторые частные случаи простейших тригонометрических уравнений, когда решение может быть записано без применения общих формул:

sinx = 0, x = πk , kϵZtgx =0, x = πk , kϵZ

sinx = 1, x = π /2 + 2π k , kϵZtgx =1, x = π /4+ πk , kϵZ

sinx = -1, x = — π /2 + 2π k , kϵZtgx =-1, x = — π /4 + πk , kϵZ

cos x = 0, x = π/2+2πk, kϵZ

cos x = 1, x = 2 π k, kϵZ

cos x = -1, x = π + 2 π k, kϵZ

Схема решения тригонометрических уравнений

Основная схема, которой мы будем руководствоваться при решении тригонометрических уравнений следующая:

Решение заданного уравнения сводится к решению элементарных уравнений.

Средства решения: преобразования, разложения на множители, замена неизвестных.

Ведущий принцип: не терять корней. Это означает, что при переходе к следующему уравнению (уравнениям) мы не опасаемся появления лишних (посторонних) корней, а заботимся лишь о том, чтобы каждое последующее уравнение нашей «цепочки» (или совокупность уравнений в случае ветвления) являлось следствием предыдущего. Одним из возможных методов отбора корней является проверка. Сразу замечу, что в случае тригонометрических уравнений трудности, связанные с отбором корней, с проверкой, как правило, резко возрастают по сравнению с алгебраическими уравнениями. Ведь проверять приходится серии, состоящие из бесконечного числа членов.

Особо следует сказать о замене неизвестных при решении тригонометрических уравнений. В большинстве случаев после нужной замены получается алгебраическое уравнение. Более того, не так уж и редки уравнения, которые, хотя и являются тригонометрическими по внешнему виду, по существу таковыми не являются, поскольку уже после первого шага — замены переменных — превращаются в алгебраические, а возращение к тригонометрии происходит лишь на этапе решения элементарных тригонометрических уравнений.

Еще раз напомню: замену неизвестного следует делать при первой возможности, получившееся после замены уравнение необходимо решить до конца, включая этап отбора корней, а уж затем возвратится к первоначальному неизвестному.

Одна из особенностей тригонометрических уравнений заключается в том, что ответ во многих случаях может быть записан различными способами. Даже для решения уравнения sinx = a (│ a │≤1)ответ может быть записан следующим образом:

1) в виде двух серий: x ₁ = arcsina +2 πk , x ₂ = π — arcsina +2 πk , kϵZ ;

2) в стандартной форме представляющей собой объединение указанных выше серий: x =(-1) k arcsina +π k , kϵZ ;

3) поскольку sinx = cos ( x -π/2), то ответ можно записать в виде x = π/2 ± arccosa +2 πk , kϵZ . (В дальнейшем наличие параметра k , n , m или l в записи ответа автоматически означает, что этот параметр принимает всевозможные целочисленные значения. (Исключения будут оговариваться.)

Очевидно, что тремя перечисленными случаями не исчерпываются все возможности для записи ответа рассматриваемого уравнения (их бесконечно много).

Обычно ответ записывается на основании пункта 2. Полезно запомнить следующую рекомендацию: если на решении уравнения sinx = a работа не заканчивается, необходимо еще провести исследование, отбор корней, то наиболее удобна форма записи, указанная в пункте 1. (Аналогичную рекомендацию следует дать и для уравнения cosx = a .)

📹 Видео

Как использовать интеграл в обычной жизни. Математик МГУ и Савватеев #shortsСкачать

#635 НАУКА Структура вакуума. Устройство Мироздания: версия Межзвездного Союза. Юмор в разных мирах.Скачать

7.5 ЧАСОВ МАТАНА!!! ПОДАРОК ВСЕМ СТУДЕНТАМ ДЛЯ ПОДГОТОВКИ К ЗАЧЁТАМ И ЭКЗАМЕНАМ ОТ ЁЖИКА В МАТАНЕ!!!Скачать

ТРИГОНОМЕТРИЯ В ЖИЗНИ И ДРУГИХ ОБЛАСТЯХ НАУКИ))Скачать

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Как использовать тригонометрию в жизни?? (Бешеный математик)Скачать

✓ Тригонометрия: с нуля и до ЕГЭ | #ТрушинLive #030 | Борис ТрушинСкачать

Решаем все типы задач № 12Скачать

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕСкачать