Где числа a b и c целые найдите значение дискриминанта уравнения

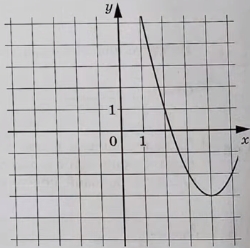
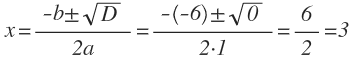На рисунке изображён график функции вида f(x) = ax 2 + bx + c, где числа a, b и c – целые. Найдите значение f (−5).

Источник: Ященко ЕГЭ 2022 (36 вар)

По графику видим, что у данной параболы коэффициент а = 1 .
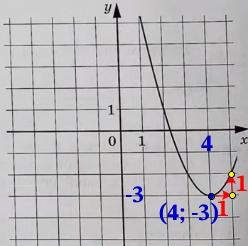
Вершина параболы находится в точке (4; –3) . Координата х вершины параболы находится по формуле:

Подставим известные значения и найдём b:

4=frac
b = –8

Подставив координаты вершины параболы х и у найдём коэффициент с:

y = ax 2 + bx + c
–3 = 1·4 2 – 8·4 + c
–3 = 16 – 32 + c
c = 13

Функция имеет вид:

Найдём f(−5):

f(–5) = 1·(–5) 2 – 8·(–5) + 13 = 25 + 40 + 13 = 78

Видео:На рис. изображен график функции f(x)=ax^2+bx+c, где числа a, b и с – целые. Найдите f(-10).Скачать

Как найти дискриминант квадратного уравнения

О чем эта статья:

Видео:По графику функции найти дискриминанта уравнения f(x)=0. Математика 10-11 класс. Егэ профиль.Скачать

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Такое уравнение можно решить с помощью формулы дискриминанта.

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Видео:ОГЭ. Задание 11. ГрафикиСкачать

Как решать квадратные уравнения через дискриминант

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

Определим, чему равны коэффициенты a, b, c.

Вычислим значение дискриминанта по формуле D = b2 − 4ac.

Если дискриминант D 0, то у уравнения две корня, равные

Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Видео:ЕГЭ задание 9 На рисунке изображен график функции вида f(x)=ax²+bx+cСкачать

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x 2 — 4x + 2 = 0.

1. Определим коэффициенты: a = 3, b = -4, c = 2.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D 2 — 6x + 9 = 0.

1. Определим коэффициенты: a = 1, b = -6, c = 9.
2. Найдем дискриминант: D = b 2 — 4ac = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0.

D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x 2 — 4x — 5 = 0.

1. Определим коэффициенты: a = 1, b = -4, c = -5.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 1 * (-5) = 16 + 20 = 36.

D > 0, значит уравнение имеет два корня:

Ответ: два корня x₁ = 5, x₂ = -1.

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Презентация «Анализ графиков (новое 9 задание). Подготовка к профильному ЕГЭ по математике»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

311 лекций для учителей,
воспитателей и психологов

Получите свидетельство
о просмотре прямо сейчас!

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Добрый день, уважаемые коллеги! Приятно видеть вас в этой аудитории, и очень надеюсь, что сегодня у нас с вами получится интересное и полезное мероприятие.

Мастер-класс
учителя математики
МОУ «СОШ№ 14»
Рискуловой Тотайхан Оразалиевны
по теме:
«Анализ графиков (новое 9 задание). Подготовка к профильному ЕГЭ по математике»
а Эдельбай
Благодарненский район

«Расскажи мне и я забуду. Покажи мне и я пойму. Позволь мне сделать самому, и я научусь»

Конфуций
Конфуций-древнекитайский проповедник,
писатель, философ.

Сложно подготовить обучающихся к сдаче экзамена. Это большой труд. Но не надо бояться. Если вы хорошо знаете, объясняете, любите свой предмет и своих учеников, вы обязательно сможете подготовить их к ЕГЭ по математике.
Важный принцип — это логичность. В шутливой манере он говорит: «нормальные герои всегда идут в обход». Нужно учиться использовать наличный запас знаний, применяя различные «хитрости» и «правдоподобные рассуждения» для ответа наиболее простым и понятным способом.
Главная заповедь учителя – заметить даже самое маленькое продвижение ученика вперёд и поддержать его успех.

Цель мастер-класса:
показать приемы решения нового 9 задания по теме «Анализ графиков»
развивать логическое мышление, память, познавательный интерес

1 9 задание
На рисунке изображены графики двух линейных функций. Найдите ординату точек пересечения.
1
2
Решение
Уравнение прямой у=kx+b. Первая прямая проходит
через точки (-4;1) и (-2;4), k= 𝟑 𝟐 .
Найдем b,подставив координаты одной из точек в уравнение
1=1,5·(-4)+ b, b=7.
у=1,5х+7-уравнение1 прямой.
2) Вторая прямая проходит через точки (-1;0) и (2;3), k= 𝟑 𝟑 =𝟏.
Найдем b,подставив координаты одной из точек в уравнение
0=1·(-1)+ b, b=1.Тогда у=х+1-уравнение2 прямой.
3)Решим систему уравнений у=𝟏,𝟓𝒙+𝟕, 𝒚=𝒙+𝟏 Вычтем из 1 уравнения 2 уравнение , получим 0=0,5х+6.Отсюда х=-12.Тогда у=-11.
Ответ:-11

9 задание
На рисунке изображен график функции f(x)= 𝒂 x²+bx+c,где числа a,b и c-целые. Найдите значение f(-12).
Решение.
f(x)= 𝒂(x-m)²+n,где m, n-координаты вершины параболы.
m= -4,n= -3, 𝒂 =1.
f(x)=(x-(-4))²+(-3),
f(x)=(x+4)²-3,
f(-12)=(-12+4)²-3,
f(-12)=61.
Ответ:61
2

9 задание
На рисунке изображен график функции f(x)= 𝒙 𝟐 𝒂 +bx+c, где числа 𝒂 ,b и c-целые. Найдите значение f(4).
Решение.
f(x)= 𝟏 𝒂 (x-m)²+n,где (m, n)-координаты вершины параболы.
По графику m= -2,n= 11, 𝒂 = -2. (Введем новую систему координат через вершину параболы, тогда график
функции f(x)= 𝒙 𝟐 𝒂 проходит через точку (2;-2).
Подставив в формулу f(x)= 𝒙 𝟐 𝒂 ,найдем а)
f(x)= — 𝟏 𝟐 (x+2)²+11= — 𝟏 𝟐 x²-2x+9,значит, 𝒂 = — 2, b=-2, c=9.
Тогда f(4)= — (𝟒+𝟐)² 𝟐 +11= — 18+11= — 7.
Ответ:- 7

9 задание. На рисунке изображен график функции f(x)= 𝒂 x²+bx+c. Найдите f(-1).
Решение.
Из рисунка видно, что график проходит через (3;2);(4;5);(5;4)
9а+3b+c= 2, 16a+4b+c=𝟓, 25a+5b+c=4.
Вычтем из 2 уравнения 1-е,
получим7a+b=𝟑
Вычтем из 3уравнения 2-е,
получим 9a+b=-𝟏
Решив систему уравнений 7a+b=𝟑, 9a+b=−1;
находим 𝒂=-2 ,b=17.
Тогда f(x)=- 2 x²+17x+c и f(3)=2, найдем ,что с=-31.
f(x)=- 2 x²+17x-31,
f(-1)=-2-17-31=-50
Ответ:-50
4

9 задание. На рисунке изображен график функции f(x)=ах²+bx+c,где числа 𝒂 ,b и c-целые. Найдите абсциссу вершины параболы.
Решение.
Абсцисса вершины параболы найдем по формуле х 𝟎 = — 𝒃 𝟐𝒂
Из рисунка видно, что f(-3)=-2; f(-2)=1; f(-1)=6.Тогда
9а−3b+c= −2, 4a−2b+c=1, a−b+c=6 ;
вычтем из 1 уравнения 2-е, получим5a-b=-𝟑
вычтем из 2 уравнения 3-е,получим 3a-b=-𝟓.
Решив систему уравнений 5a−b=−𝟑, 3a−b=−𝟓; находим 𝒂=1 ,b=8.
Абсцисса вершины параболы х 𝟎 = — 𝒃 𝟐𝒂 =-4.
Ответ:-4

7
9 задание. На рисунке изображены графики функций f(x)=5х+9 и g(x)= ах²+bx+c, которые пересекаются в точках А и В. Найдите абсциссу точки B

Решение. По графику с=-3.График функции g(x) проходит через точки (-2;-1);(-1;-3);(2;3).
Подставим координаты точки (-1;-3), получим
-3=а- b-3.Отсюда а=b.
g(x)= ах²+аx-3.
Подставим координаты точки (2;3), получим, что а=1.
g(x)= х²+x-3.
Чтобы найти абсциссу точки ,нужно решить уравнение х²+x-3=5х+9,
х²-4x-12=0.
По теореме Виета х 𝟏 ·х 𝟐 =-12, х 𝟏 + х 𝟐 =4
По графику х 𝟏 =-2, тогда х 𝟐 =6.
Ответ:6

Решение.
f(x)= 𝒂(x-m)²+n,где m, n-координаты вершины параболы.
m=-3,n=3, 𝒂 =1.
f(x)=(x-(-3))²+3
f(x)=(x+3)²+3,
f(x)=х²+6х+12, так как f(x)=0.
то х²+6х+12=0
D=6²-4·1·12= -12.
Ответ:-12
Решите 9 задание
На рисунке изображен график функции f(x)= 𝒂x²+bx+c,где числа 𝒂 ,b и c-целые. Найдите значение дискриминанта уравнения f(x)=0.
8

Решение.
|bx+c|=0 в точке излома. Значит, bx+c=0 при х=2.

9 задание
На рисунке изображен график функции вида 𝒇 𝒙 = 𝒂 x+|bx+c|+d, где числа 𝒂,b, c и d-целые.
Найдите корень уравнения bx+c=0

9 задание.
На рисунке изображён график функции вида f(x)=ax + |bx + c| +d, где числа a, b, c и d — целые. Найдите корень уравнения ax + d=0.

Решение.
|bx + c|=0 в точке излома при х=1,
Если х 1,то f(x)=ax +bx + c +d=(а+b)х+с+ d, где а+b-угловой коэффициент, по графику а+b=2.
Продолжив прямую до пересечения с осью Оу, получим , что с+ d =-1.

Решив эти системы а−b=−4 а+b=𝟐 и с+ d =−1 d−с=5 , получим,что
a=-1;b=3;c=-3;d=2. Подставив найденные значения в уравнение ax +d=0 , получим -x + 2=0,
х=2.
Ответ:2

11 На рисунке изображен график функции вида f(x)= 𝒂 cos(bπx+c)+d, где числа 𝒂,b, c и d-целые. Найдите 𝒇 𝟏𝟎𝟎 𝟑 .
Решение.
По графику 𝒇 𝒎𝒂𝒙 =𝟏,𝒇 𝒎𝒊𝒏 =-3
d= 𝒇 𝒎𝒂𝒙 + 𝒇 𝒎𝒊𝒏 𝟐 = 𝟏−𝟑 𝟐 = -1. |a|= 𝒇 𝒎𝒂𝒙 − 𝒇 𝒎𝒊𝒏 𝟐 = 𝟏+𝟑 𝟐 =2.
По графику 𝒂 =2, c=0, T=2
T= 𝟐𝝅 𝒃𝝅 = 𝟐 𝒃 , то есть 𝟐 𝒃 =2, отсюда b=1
f(x)=2cosπx-1,
f 𝟏𝟎𝟎 𝟑 =f 𝟗𝟔 𝟑 + 𝟒 𝟑 =𝒇 𝟑𝟐+ 𝟒 𝟑 =f 𝟒 𝟑 ,
f 𝟒 𝟑 =2cosπ· 𝟒 𝟑 -1 = 2cos 𝟒 𝟑 π-1 = 2cos π+ π 𝟑 -1= -2cos π 𝟑 −1= -2.
Ответ:-2

9 задание. На рисунке изображен график функции f(x)=k х. Найдите f(2,56)
Решение.
График этой функции проходит через точку (4;-3).Подставив координаты этой точки, получим
-3=k 𝟒 ,
2k=-3,
k =-1,5.
f(2,56)=-1,5 𝟐,𝟓𝟔 =−1,5·1,6=−2,4.

9 задание. На рисунке изображен график функции f(x)= 𝒌 𝒙 +a. Найдите f (0,25)

Решение. График функции имеет горизонтальную асимптоту y=-2, значит, а=-2.
(График функции f(x)= 𝒌 𝒙 +a получается сдвигом графика функции f(x)= 𝒌 𝒙 вдоль оси Оу на величину |а| вверх, если а>0 и вниз если a 0 и вправо если a 0 и вниз если b 0 и вправо если b

Курс повышения квалификации

Основы разработки онлайн-курса

• Сейчас обучается 47 человек из 20 регионов

Курс повышения квалификации

Использование современных информационных технологий и интерактивных сред электронного обучения в организации образовательного процесса в школе в условиях сложной санитарно-эпидемиологической обстановки с учетом требований ФГОС

Курс повышения квалификации

Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО

• Сейчас обучается 174 человека из 53 регионов

«Обзор традиционных и современных методик для формирования навыков арифметических вычислений в уме у младших школьников»

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Видео:РАЗБИРАЕМ ДИСКРИМИНАНТ ЧАСТЬ I #shorts #математика #егэ #огэ #дискриминантСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 859 010 материалов в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 20.10.2021
• 355
• 7

• 20.10.2021
• 1399
• 17

• 20.10.2021
• 80
• 0

• 20.10.2021
• 186
• 2

• 20.10.2021
• 261
• 1

• 20.10.2021
• 208
• 3

• 20.10.2021
• 183
• 0

• 20.10.2021
• 242
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 20.10.2021 18184
• PPTX 5.1 мбайт
• 1438 скачиваний
• Рейтинг: 4 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Рискулова Тотайхан Оразалиевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 2 месяца
• Подписчики: 0
• Всего просмотров: 36490
• Всего материалов: 8

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

«Навыки эффективного решения проблем»

«Формирование основ гендерной социализации у детей дошкольного возраста»

«Использование элементов технологии ТРИЗ для активизации познавательной деятельности»

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Тысячи учителей в Австралии вышли на забастовку

Время чтения: 2 минуты

Минобрнауки выделило более 590 тысяч бюджетных мест на 2023-24 учебный год

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:✓ Четыре способа решить новую задачу из ЕГЭ | Задание 10. Демоверсия ЕГЭ-2023 | Борис ТрушинСкачать

Квадратное уравнение. Дискриминант. Теорема Виета.

теория по математике 📈 уравнения

Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.

Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.

Видео:Решение квадратных уравнений. Дискриминант. Практическая часть. 3ч. 8 класс.Скачать

Дискриминант

Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).

Нахождение корней квадратного уравнения

Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:

D=b 2 –4ac

Если D>0, то уравнение имеет два различных

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

Пример №2. Решить уравнение 5х 2 +2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b 2 –4ac=2 2 –4=4–20=–16, D 2 –6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.

D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Видео:34 Задача: Найти корни квадратного уравнения при помощи PythonСкачать

Теорема Виета

Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.

Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.

Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.

Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:

Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.

Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:

Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:

Данное уравнение является квадратным. Но в его условии присутствует квадратный

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.

Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):

х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0

Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:

х 2 − 2 х − 24 = 0

Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.

Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .

pазбирался: Даниил Романович | обсудить разбор | оценить

📽️ Видео

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

ЛОВИ ПРОДОЛЖЕНИЕ 😉 ДИСКРИМИНАТ ЧАСТЬ II #shorts #математика #егэ #огэ #профильныйегэСкачать

Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать

Как решают уравнения в России и СШАСкачать

Задание 9. ЕГЭ профиль. Парабола.Скачать

Как решать квадратные уравнения без дискриминантаСкачать

Квадратное уравнение. Как решить? | Математика ОГЭ 2023 | УмскулСкачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать