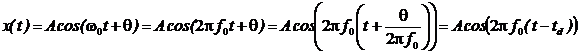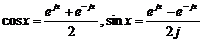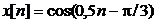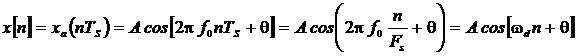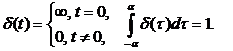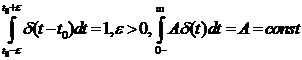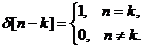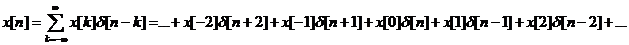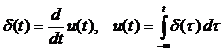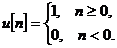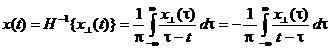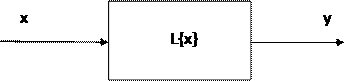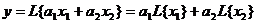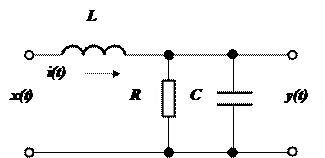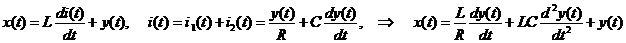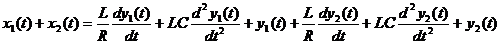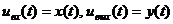Гармонический сигнал и его уравнение (3 видео)

Портал ТОЭ

Содержание

1.4 Комплексное представление гармонических сигналов
Гармонические колебания
Пару слов о матчасти
Переходим к практическим упражнениям!
Пишем свой анализатор спектра
Гармонический сигнал и его уравнение
🌟 Видео

1.4 Комплексное представление гармонических сигналов

Во многих задачах анализа электрических цепей источники электрической энергии имеют переменное во времени напряжение (ток), изменяющееся, например, по гармоническому закону:

где	A _m	– амплитуда колебаний;
ω	– угловая частота, рад/с; ( ω = 2 πf = )
ψ ₀	– начальная фаза;
f	– циклическая частота, Гц;
T	– период колебаний, с;
– фаза в момент времени t .

Гармонические колебания характеризуются также интегральными параметрами:

среднее значение за полупериод (среднее значение за период равно нулю) A _ср = ∫ ₀ T∕ 2 a ( t ) dt = ≈ 0 , 638 A _m ;
действующее значение A = = ≈ 0 , 707 A _m .

Физический смысл действующего значения тока: он равен такому постоянному току, который, проходя по активному сопротивлению, выделяет за время T то же количество теплоты, что и гармонический ток.

Расчёт цепи облегчается, если изобразить грамонические величины векторами на комплексной плоскости.

Известно, что каждая точка на комплексной плоскости определяется радиус-вектором этой точки, т.е. вектором, начало которого совпадает с началом координат, а конец находится в точке, соответствующей заданному комплексному числу.

Данное число можно записать в показательной форме (в полярной системе координат):

где A – модуль, ψ – аргумент (фаза);
( j = , в электротехнике i = не используется, т.к. этой буквой обозначается ток).

Применив формулу Эйлера, можно получить тригонометрическую форму записи:

Либо алгебраическую форму (в прямоугольных координатах):

Вектор, вращающийся в положительном направлении (против хода часовой стрелки) с угловой скоростью ω может быть выражен следующим образом:

где Ȧ _m = A _m e jψ – комплексная амплитуда, равная вектору в момент времени t = 0 .

Множитель e jωt – оператор вращения. Умножение комплексной амплитуды Ȧ _m на e jωt означает поворот вектора Ȧ _m на угол ( ωt ) в положительном направлении (против часовой стрелки).

Записывая комплексную функцию в тригонометрической форме заключаем, что функция A _m sin ( ωt + ψ ) может быть рассмотрена как мнимая часть комплексной функции, взятая без множителя j , или , что тоже самое, как проекция вращающегося вектора на мнимую ось.

Комплексное действующее значение отличается от комплексной амплитуды в раз:

Если гармонические функции имеют одну и ту же частоту, то соответствующие этим функциям векторы вращаются с одинаковой скоростью, т.е. углы между ними сохраняются неизменными. На рисунке показаны две синусоидальные функции, фазовый сдвиг равен φ = ψ ₁ − ( − ψ ₂ ) = ψ ₁ + ψ ₂ .

При равенстве начальных фаз векторы направлены в одну и ту же сторону (совпадают по фазе).

Диаграмма, изображающая совокупность векторов на косплексной плоскости, которые представляют собой гармонически изменяющиеся функции, называется векторной диаграммой .

Векторное представление гармонических функций, частоты которых одинаковы, облегчает операции сложения и вычитания этих функций.

Сумме двух функций Ȧ _{1 m} и Ȧ _{2 m} соответствует вектор ( Ȧ _{1 m} + Ȧ _{2 m} ) .

Значительно упрощаются операции дифференцирования и интегрирования функций, представленных комплексными числами.

Операция дифференцирования гармонической функции заменяется умножением на jω её комплексного изображения.

Для производной n -го порядка

Операция интегрирования гармонической функции заменяется делением на jω её комплексного изображения.

Видео:Колебаться? Показываю как. Гармонический сигнал 🔊Скачать

Гармонические колебания

На хабре было несколько статей по преобразованию Фурье и о всяких красивостях типа Цифровой Обработки Сигналов (ЦОС), но неискушённому пользователю совершенно не понятно, зачем всё это нужно и где, а главное как это применить.

АЧХ шума.

Лично мне после прочтения этих статей (например, этой ) не стало понятно, что это и зачем оно нужно в реальной жизни, хотя было интересно и красиво.
Хочется не просто поглядеть красивые картинки, а так сказать, ощутить нутром, что и как работает. И я приведу конкретный пример с генерацией и обработкой звуковых файлов. Можно будет и послушать звук, и поглядеть его спектр, и понять, почему это так.
Статья не будет интересна тем, кто владеет теорией функций комплексной переменной, ЦОС и прочими страшными темами. Она скорее для любопытствующих, школьников, студентов и им сочувствующих :).

Сразу оговорюсь, я не математик, и многие вещи могу даже сказать неправильно (поправляйте личным сообщением), и данную статью пишу, опираясь на собственный опыт и собственное понимание текущих процессов. Если вы готовы, то поехали.

Пару слов о матчасти

Если мы вспомним школьный курс математики, то для построения графика синуса мы использовали круг. В общем-то так и получается, что вращательное движение можно превратить в синусоиду (как и любое гармоническое колебание). Самое лучшая иллюстрация этого процесса приведена в википедии

Гармонические колебания

Т.е. фактически график синуса получается из вращения вектора, который описывается формулой:

f(x) = A sin (ωt + φ),

где A — длина вектора (амплитуда колебаний), φ — начальный угол (фаза) вектора в нулевой момент времени, ω — угловая скорость вращения, которая равна:

ω=2 πf, где f — частота в Герцах.

Как мы видим, что зная частоту сигнала, амплитуду и угол, мы можем построить гармонический сигнал.

Магия начинается тогда, когда оказывается, что представление абсолютно любого сигнала можно представить в виде суммы (зачастую бесконечной) различных синусоид. Иначе говоря, в виде ряда Фурье.
Я приведу пример из английской википедии. Для примера возьмём пилообразный сигнал.

Пилообразный сигнал

Его сумма будет представлена следующей формулой:

Если мы будем по очерёдно суммировать, брать сначала n=1, затем n=2 и т.д., то увидим, как у нас гармонический синусоидальный сигнал постепенно превращается в пилу:

Наверное красивее всего это иллюстрирует одна программа, найденная мной на просторах сети. Выше уже говорилось, что график синуса является проекцией вращающегося вектора, а как же быть в случае более сложных сигналов? Это, как ни странно, проекция множества вращающихся векторов, а точнее их суммы, и выглядит это всё так:

Вектора рисуют пилу.

Вообще рекомендую сходить самим по ссылке и попробовать самим поиграться с параметрами, и посмотреть как меняется сигнал. ИМХО более наглядной игрушки для понимания я ещё не встречал.

Ещё следует заметить, что есть обратная процедура, позволяющая получить из данного сигнала частоту, амплитуду и начальную фазу (угол), которое называется Преобразование Фурье.

Разложение в ряд Фурье некоторых известных периодических функций (отсюда)

Я детально на нём останавливаться не буду, но покажу, как это можно применить по жизни. В списке литературы порекомендую то, где можно почитать подробнее о матчасти.

Переходим к практическим упражнениям!

Мне кажется, что каждый студент задаётся вопросом, сидя на лекции, например по матану: зачем мне весь этот бред? И как правило, не найдя ответа в обозримом будущем, к сожалению, теряет интерес к предмету. Поэтому я сразу покажу практическое применение данных знаний, а вы эти знания уже будете осваивать сами :).

Всё дальнейшее я буду реализовывать на сях. Делал всё, конечно, под Linux, но никакой специфики не использовал, по идее программа будет компилироваться и работать под другими платформами.

Для начала напишем программу для формирования звукового файла. Был взят wav-файл, как самый простой. Прочитать про его структуру можно тут.
Если кратко, то структура wav-файла описывается так: заголовок, который описывает формат файла, и далее идёт (в нашем случае) массив 16-ти битных данных (остроконечник) длиной: частота_дискретизации*t секунд или 44100*t штук.

Для формирования звукового файла был взят пример здесь. Я его немного модифицировал, исправил ошибки, и окончательная версия с моими правками теперь лежит на гитхабе тут

Сгенерируем двухсекундный звуковой файл с чистым синусом частотой 100 Гц. Для этого модифицируем программу таким образом:

Обращаю внимание, что формула чистого синуса соответствует той, о которой мы говорили выше. Амплитуда 32000 (можно было взять 32767) соответствует значению, которое может принимать 16-ти битное число (от минус 32767 до плюс 32767).

В результате получаем следующий файл (можно его даже послушать любой звуковоспроизводящей программой). Откроем данный файл audacity и увидим, что график сигнала в действительности соответствует чистому синусу:

Чистый ламповый синус

Поглядим спектр этого синуса (Анализ->Построить график спектра)

График спектра

Виден чистый пик на 100 Гц (логарифмический масштаб). Что такое спектр? Это амплитудно-частотная характеристика. Существует ещё фазочастотная характеристика. Если помните, выше я говорил, что для построения сигнала надо знать его частоту, амплитуду и фазу? Так вот, можно из сигнала получить эти параметры. В данном случае у нас график соответствий частот амплитуде, при чём амплитуда у нас не в реальных единицах, а в Децибелах.

Величина, выраженная в децибелах, численно равна десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять.

В данном случае просто логарифм амплитуды, умноженный на 10. Логарифмический масштаб удобно использовать при работе с сигналами.

Мне, честно говоря, не очень нравится анализатор спектра в этой программе, поэтому я решил написать свой ~~с блекджеком и шлюхами~~, тем более, что это несложно.

Пишем свой анализатор спектра

Здесь может быть скучно, поэтому можете перейти сразу к следующей главе.

Поскольку я прекрасно понимаю, что тут портянки кода размещать нет смысла, те, кому реально интересно — сами найдут и поковыряют, а тем, кому это неинтересно, будут скучать, то я остановлюсь только на основных моментах написания анализатора спектра wav-файла.

Во-первых, нам wav-файл необходимо читать. Там необходимо прочитать заголовок, чтобы понять, что содержит данный файл. Я не стал реализовывать море вариантов чтения данного файла, а остановился только на одном. Пример чтения файла был взят отсюда практически без изменений, ИМХО — отличный пример. Там же есть реализация на питоне.

Следующее, что нам нужно, это быстрое преобразование Фурье. Это то самое преобразование, которое позволяет получить из конечного набора точек вектора исходных сигналов. Пусть вас пока это не пугает, дальше я объясню.
Опять же, велосипед изобретать не стал, а взял готовый пример отсюда.

Я понимаю, что чтобы объяснить, как работает программа, надо объяснить, что такое быстрое преобразование Фурье, а это как минимум ещё на одну некислую статью.

Для начала алокируем массивы:

Скажу лишь, что в программе мы читаем данные в массив длиной size_array (которое берём из заголовка wav-файла).

Массив для быстрого преобразования Фурье должен представлять собой последовательность , где fft_size=1

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Гармонический сигнал и его уравнение

Некоторые специальные сигналы

Такие сигналы (функции) широко используются в задачах обработки сигналов.

1. Гармонические сигналы (гармоники)
а) Косинусоидальная гармоника непрерывного времени (НВ)

Это обычная тригонометрическая функция косинуса

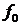
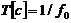
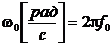
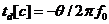
Параметры: амплитуда А, частота [ Гц], период , угловая частота, , θ [рад] – начальная фаза в радианах, — временной сдвиг (задержка) в секундах.

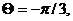
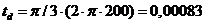
В данном примере A = 2, f ₀ = 200 Гц, с.

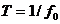
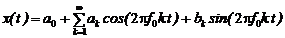
В дальнейшем будет показано, что любой периодический сигнал x ( t ) с периодом можно представить в виде бесконечной суммы гармоник (рядом Фурье)

Такое представление очень важно и продуктивно для многих прикладных наук, в том числе для обработки сигналов.

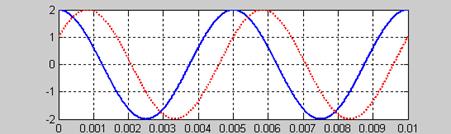
Геометрическая интерпретация гармонического сигнала .

Вектор А вращается против часовой стрелки с частотой f или скоростью 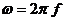радиан/с .

Проекция вектора А на горизонтальную ось – это значения косинусоидальной гармоники с амплитудой А, на вертикальную ось — значения синусоидальной гармоники. Частота f = 2 Гц означает, что точка делает 2 оборота в сек.

Если вектор делает один оборот за Т секунд, то угловая скорость (частота) составляет 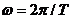рад/с. Θ – начальная фаза (начальный угол) вектора относительно оси абсцисс.

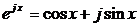
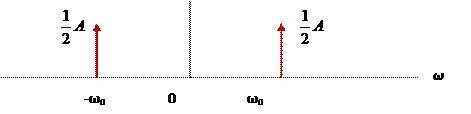
По формуле Эйлера . Отсюда

Действительная гармоника может быть представлена также как сумма проекций двух комплексных гармоник. Одна – проекция вектора половинной амплитуды, вращающегося против часовой стрелке со скоростью ω рад/с , вторая – такая же проекция вектора, вращающегося по часовой стрелке со скоростью — ω рад/с. Первая проекция называется синфазной составляющей, вторая – квадратурной.

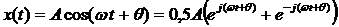
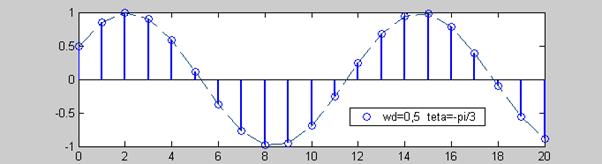
Представление действительной гармоники в виде суммы комплексных гармоник . Её график в частотной области

б) Гармоника дискретного времени (ДВ)

, n- номер отсчета. Пример:

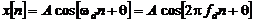
Такая гармоника получается дискретизацией (взятием отсчетов, англ. s ampling ) из аналоговой гармоники с интервалом (периодом) отсчетов Т _S =1/ F_S или частотой отсчетов F_S :

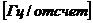
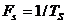
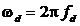
При этом f _d = f ₀ / F_S – нормированная частота в Гц на отсчет , — скорость, или частота отсчетов, — угловая нормированная частота в радианах в секунду на отсчет, . Её называют также цифровой частотой.

Дискретная гармоника периодична с периодом 2π. Действительно

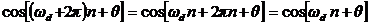
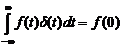
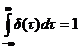
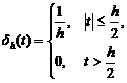
2. Дельта-функция (другое название – единичная импульсная функция или функция Дирака). Это особого вида функция δ( t ), определяемая следующим интегралом . Отсюда, полагая f ( t )=1 , получаем условие для площади дельта – функции . Т.о., площадь дельта – функции равна 1. Интуитивное определение дельта — функции, как предела прямоугольного импульса единичной площади

. График

Как следствие,

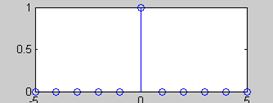
Условное графическое изображение дельта – функции

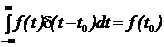
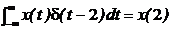
Дельта-функция имеет строгий математический смысл только в том случае, когда она используется под знаком интеграла, — свойство фильтрации или отсчета функции f ( t ) , например, .

3. Единичный импульс . Играет ту же роль для дискретных систем, что и

что и δ – функция для непрерывных систем.

Соответственно

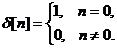
С помощью единичного импульса произвольный дискретный сигнал (последовательность … x (0), x (1), x (2), …) может быть записан как сумма вида

4. Единичная ступенчатая функция (сигнал)
как следствие

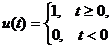
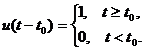
Функция u ( t ) имеет разрыв (скачок) при t = 0.

Связь между ступенчатой функцией u ( t ) и дельта – функцией δ( t )

. Единичная импульсная последовательность

6. Аналитические сигналы

В системах передачи информации (системах связи) очень часто используются узкополосные сигналы вида . Функция A ( t ) такого сигнала называется амплитудной огибающей, а θ( t ) – фазовой функцией сигнала. Математически такие сигналы удобно описывать как комплексные . При этом действительный сигнал x ( t ) является вещественной частью комплексного сигнала z ( t ), т.е. .

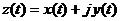
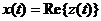
Частным, широко используемым на практике случаем комплексного сигнала является аналитический сигнал

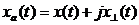
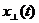
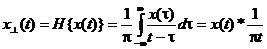
в котором мнимая часть вычисляется с помощью преобразования Гильберта ( Hilbert transformation ) .

Обратное преобразование Гильберта

определяет сам сигнал x ( t ) по его преобразованию Гильберта .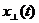

Понятие системы. Линейные системы.

В широком смысле системой называют совокупность элементов, взаимосвязанных между собой таким образом, что возникает определенная целостность, единство. Система обладает свойством иерархичности, в соответствии с которым каждый компонент (элемент) системы может также рассматриваться как система, а данная система может являться элементом более широкой системы.

В данном курсе рассматриваются линейные системы преобразований сигнала с одним входом и одним выходом. При этом физическая природа систем не рассматривается, точнее, она не имеет главного значения. Разные физические системы могут описываться одинаковыми уравнениями.

Обозначение y = L ( x ) означает формальное описание преобразования входного сигнала x в выходной y . Общее графическое обозначение,

L – это оператор преобразования системы, т.е. правило (уравнение, функция, алгоритм) преобразования множества X (входных сигналов) в множество Y ( выходных сигналов).

Непрерывные (аналоговые) системы, такие, как устройства аналоговой электроники или датчик температуры, имеют непрерывный во времени входной x ( t ) и выходной сигналы y ( t ) . У дискретных (цифровых) систем входной x [ n ] и выходной сигналы y [ n ] – дискретные во времени, как, например, в компьютерах или цифровых процессорах.

В линейных системах оператор должен обладать свойством суперпозиции, т.е.

В частности, для линейных систем нулевой вход влечет нулевой выход

Основным видом оператора системы является уравнение связи выходного и входного сигналов. Для линейных систем уравнение является линейным. Большой класс реальных систем, но не все, описывается линейными дифференциальными и разностными уравнениями.

Примеры линейных систем.

Линейными являются линейные электрические цепи, например, LRC – цепь (контур)

Уравнения цепи. Из законов Киргофа

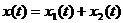
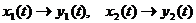
Если , и , то

Т.е. сумме входных сигналов соответствует сумма выходных сигналов – линейная система.

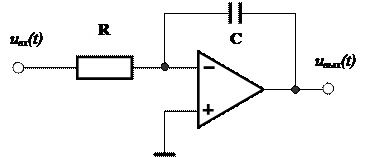
2. Линейная активная электрическая цепь, например, интегратор

В обозначениях курса ТОС:

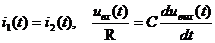
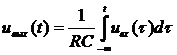
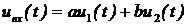
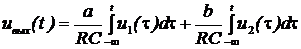
Уравнения системы: , если , то , т.е. система является линейной.

3. Линейные дискретные системы, описываемые линейными разностными уравнениями.

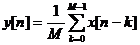
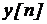
Например, дискретный фильтр текущего усреднения с уравнением , при этом М – число усредняемых точек. В этом фильтре каждая точка выходного сигнала определяется как среднее арифметическое предыдущих М точек входного сигнала, в результате — уменьшаются шумы Система – линейная, что легко проверяется .

Для нелинейных систем принцип суперпозиции неприменим. Поэтому анализ нелинейных систем значительно сложнее, чем линейных.

Примеры нелинейных систем: системы со статическими нелинейными характеристиками, например, транзисторы, диоды, а также умножители сигналов, электронные устройства типа модуляторов, детекторов, преобразователи формы сигналов и др.

Многие нелинейные системы являются линейными в режиме малого сигнала, например, транзисторные усилители, операционные усилители, что упрощает их анализ.

Нелинейные системы в данном курсе не рассматриваются.

Безынерционные и инерционные системы

Система является безынерционной или системой без памяти ( memoryless system ), если её выходной сигнал зависит только от настоящих значений входного сигнала, но не зависит от прошлых и будущих значений. В противном случае система является инерционной или системой с памятью ( memory system ). Например, квадратор с уравнением 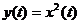— это безынерционная нелинейная система. Любая цепь, состоящая только из резисторов – безинерционная , т.к. резистор — безынерционный элемент.

Другой пример. RC – цепь (фильтр нижних частот) с уравнением 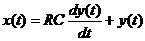— это система (цепь) с памятью (инерционная).

Физически реализуемые (каузальные) системы

Физически реализуемой, или каузальной (англ. caus е — причина ) является система, выходной сигнал которой в момент времени t ₀ зависит только от прошлых и настоящих значений входного сигнала, но не от будущих.

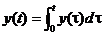
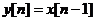
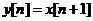
Пример каузальных систем: интегратор или цепь задержки . Некаузальная система: . Все системы реального времени – каузальные. Время изменяется только вперед. Но системы, обрабатывающие данные, сохраненные в памяти ( off – line systems ) процессора, могут быть некаузальными.

Некаузальными могут быть систем с пространственными переменными, обычно обозначаемыми как x , y и др. Пространственная переменная может изменяться в любом направлении.

Стационарные (инвариантные во времени) системы

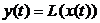
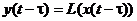
Система является стационарной, или инвариантной во времени ( англ. time invariance system ), если временной сдвиг сигнала на входе вызывает такой же сдвиг сигнала на выходе системы. Для стационарной системы непрерывного времени справедливо, если , то . Стационарные системы – это системы с постоянными во времени параметрами. Во многих практических задачах обоснованно предполагается стационарность системы, что упрощает их анализ. В данном курсе рассматриваются только линейные инвариантные во времени системы ( ЛИВ или ЛСС системы). Англ. LTI systems — линейные инвариантные во времени системы .

Устойчивые и неустойчивые системы

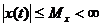
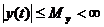
Если ограниченному входному сигналу всегда соответствует ограниченный выходной сигнал , то система является устойчивой. Мнемоника: ограниченный вход à ограниченный выход (ОВОВ).

Для большинства (но не всех!) систем устойчивость является обязательным условием их работоспособности.

Например, система – усилитель

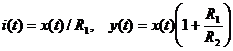
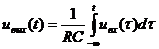
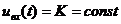
с уравнением — устойчивая система, ограниченному входу соответствует ограниченный выход. Интегратор с уравнением ) (см. схему выше) — неустойчивая система, поскольку, если , то выходной сигнал неограниченно возрастает с увеличением времени интегрирования t .

· В анализе и синтезе систем широко используются специальные сигналы, такие как
— дельта функция 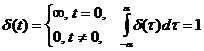, — для систем НВ,
— единичный импульс 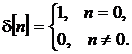, — для систем ДВ,
— единичная ступенчатая функция

— единичная импульсная последовательность 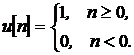, для систем ДВ
— гармонический сигнал (гармоника) .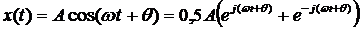

· Система – это объект (устройство), в котором определены связи между входными и выходными сигналами в соответствии с его структурой и параметрами.
Системы подразделяют на:

— линейные и нелинейные – важнейший признак классификации для обработки сигналов,

— инерционные и безынерционные ,

— стационарные и нестационарные,

— каузальные (физически реализуемые) и некаузальные,