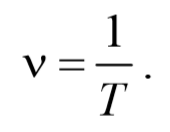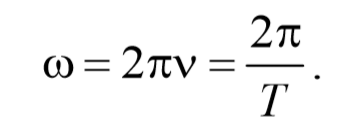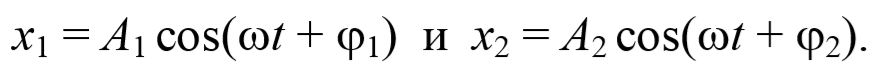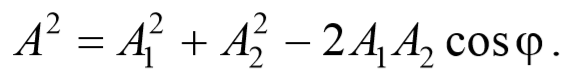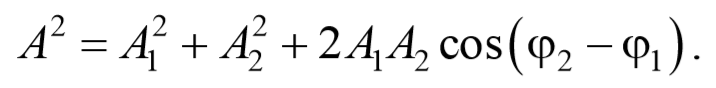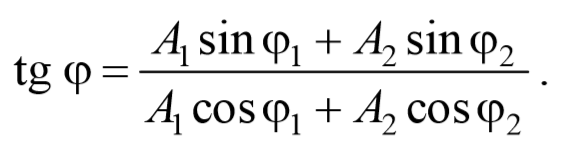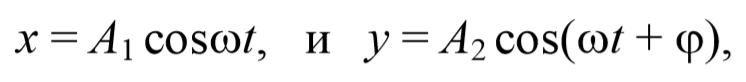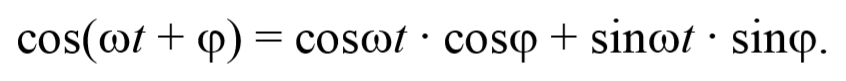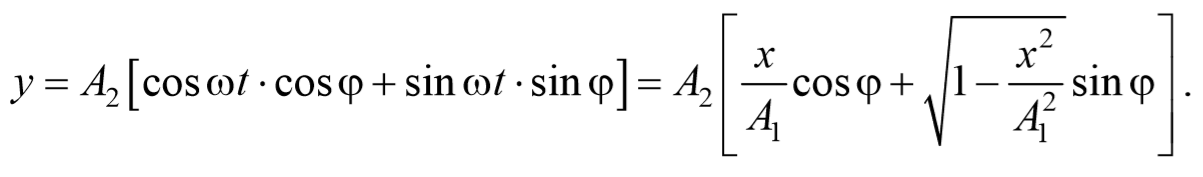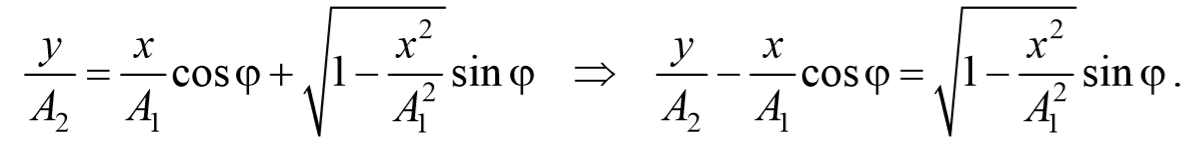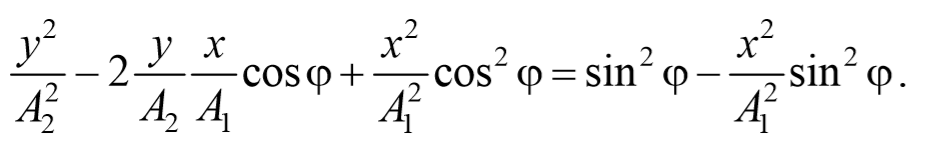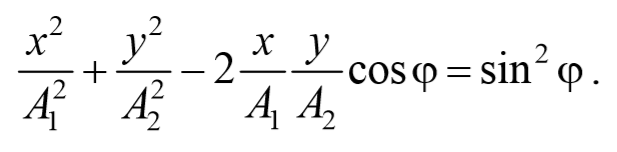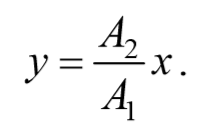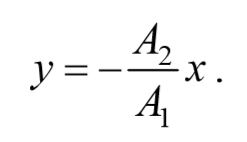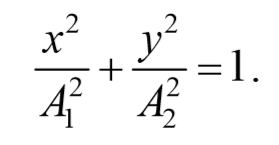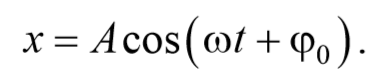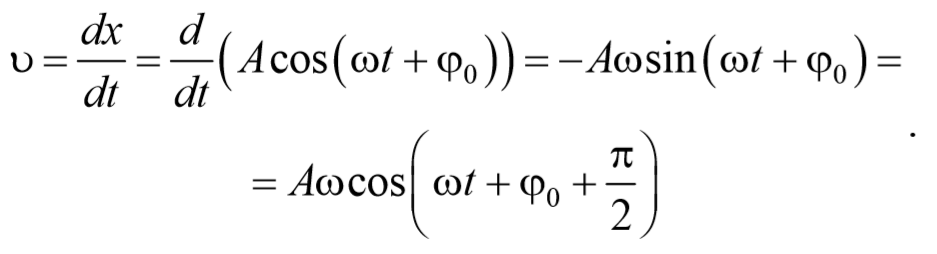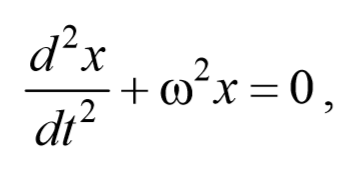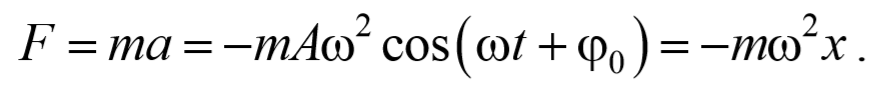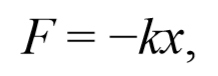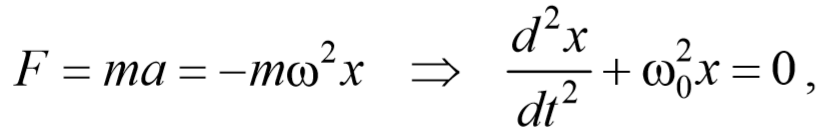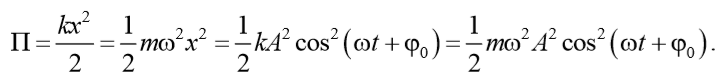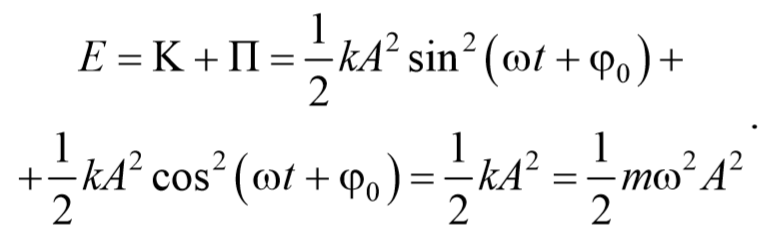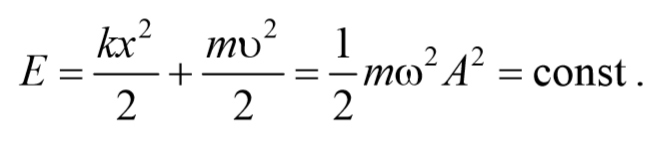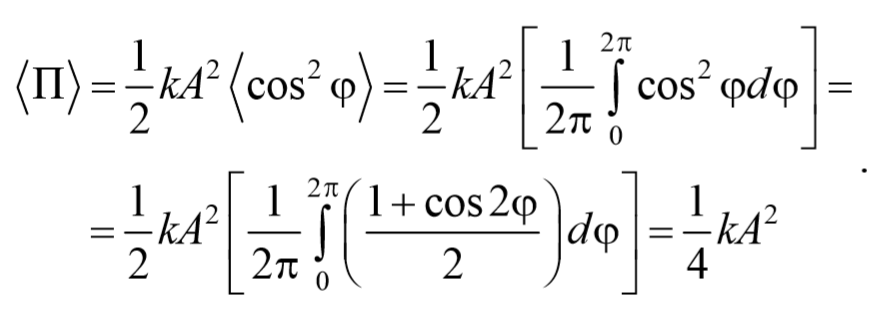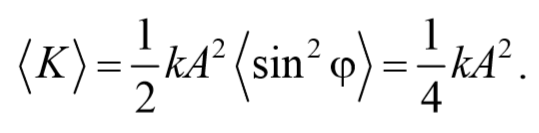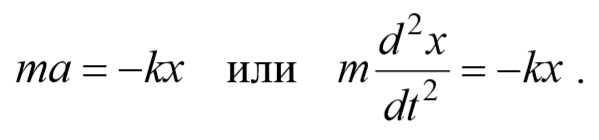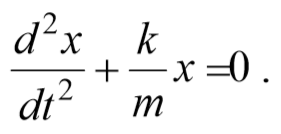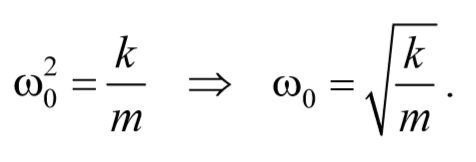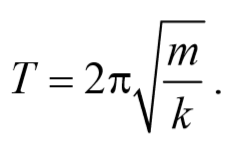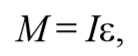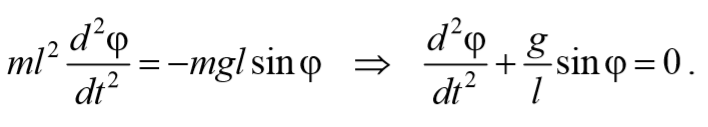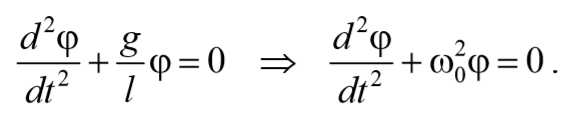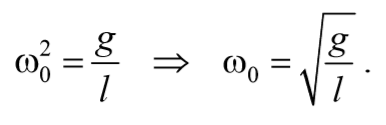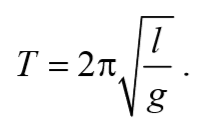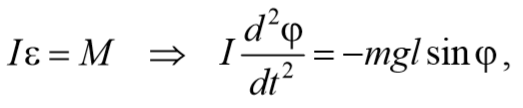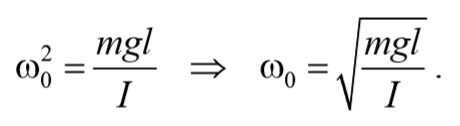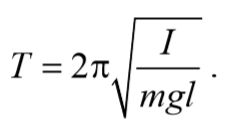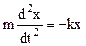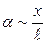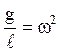Гармонический осциллятор дифференциальное уравнение и его решение математический маятник (4 видео)

Гармонический осциллятор. Пружинный, физический и математический маятник (малые колебания)

Ознакомившись с закономерностями и характеристиками гармонических колебаний, применим полученные знания для изучения гармонического осциллятора. Силами трения будем пренебрегать.

Гармоническим осциллятором называется система, совершающая гармонические колебания, описываемые дифференциальным уравнением, имеющим вид (7.7):

Примерами гармонического осциллятора являются пружинный, математический и физический маятники.

Маятник — твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или оси.

Пружинный маятник — груз массой т, подвешенный на абсолютно упругой пружине, массой которой можно пренебречь, и совершающий гармонические колебания под действием упругой силы F_x=

kx, где к — жесткость пружины.

Пусть /₀ — длина нерастянутой пружины (рис. 7.3). Под действием веса тела пружина растянется на А/₀ и тело займет положение равновесия

Рис. 7.3. Пружинный маятник x = 0 . В этом положении сила тяжести mg уравновешивается упругой силой кА1₍₎:

Выберем ось X, направленную вниз. Если сместить тело вниз на расстояние х, то удлинение пружины составит Д/₀+х. Так как со стороны растянутой пружины действует сила, направленная вверх, то действующая на тело результирующая сила

С учетом уравнения (7.11) можно сделать вывод, что результирующая сила F_x=—kx имеет характер квазиупругой силы. Поэтому груз будет совершать гармонические колебания. По второму закону Ньютона (3.3) получаем уравнение движения пружинного маятника вида (7.7):

Следовательно, решение дифференциального уравнения где циклическая частота и период будут соответственно

Кинетическая энергия пружинного маятника будет выражаться как

Математическим маятником называется идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой нити длиной / и колеблющейся под действием силы тяжести без трения.

Небольшой тяжелый шарик, подвешенный на тонкой длинной нити, когда размерами тела по сравнению с длиной нити можно пренебречь, является хорошим приближением математического маятника.

При малых углах отклонения а можно считать х

а/, где х — линейное смещение вдоль траектории точечной массы (шарика) от положения равновесия в точке О (рис. 7.4). Если возвращающая сила пропорциональна х или а, то колебания будут гармоническими. Возвращающая сила — составляющая силы тяжести груза, касательная к траектории шарика — определяется так:

Puc. 7.4. Математический маятник

Уравнение движения записывается как

т.е. имеет вид закона (7.1). Тогда частота и период колебаний определяются как

Следовательно, частота малых колебаний зависит от длины маятника

/ /2 , но не от массы тела. Формула (7.15) для периода колебаний математического маятника называется формулой Томсона. Согласно (7.15), период колебаний математического маятника пропорционален его длине в степени 1/2.

Рис. 7.5. Физический маятник

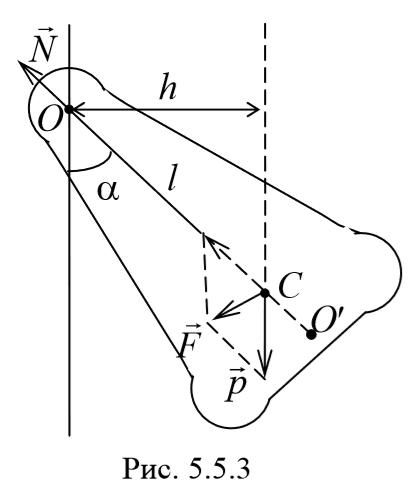
Физический маятник — твердое тело, совершающее под действием силы тяжести колебания вокруг горизонтальной неподвижной оси, не проходящей через центр масс тела и называемой осью подвеса маятника.

В данном случае тело нельзя рассматривать как материальную точку. Ось вращения жестко связана с телом.

Выберем положительное направление отсчета угла а против часовой стрелки; ось вращения Z, проходящая через точку подвеса О, направлена на нас (рис. 7.5).

Пусть физический маятник отклонен из положения равновесия на некоторый угол а. Тогда

уравнение вращательного движения маятника в проекции на ось Z (см. уравнение динамики вращательного движения твердого тела (5.8)) примет вид

где М, — момент возвращающей силы; / — момент инерции маятника от-

носительно оси вращения Z; —рр = -jp- — угловое ускорение.

Колебания физического маятника будут гармоническими только тогда, когда since-а (малые углы отклонения). Проекция момента силы тяжести на ось Z

где F_T =— mg-since — возвращающая сила; / — расстояние между точкой подвеса и центром масс С маятника; /since — плечо силы.

Тогда для малых амплитуд можно записать уравнение колебаний физического маятника

Решением дифференциального уравнения является функция а = а_т • cos(co₀/ + ер) с циклической частотой и периодом

где длина /_п =—- — приведенная длина физического маятника. Заметим, ф ml

что квазиупругим в рассмотренном случае является момент силы тяжести, пропорциональный углу отклонения а.

Приведенная длина I физического маятника — это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Точка О’ на продолжении прямой ОС, отстоящая от оси подвеса на расстоянии / , называется центром качания физического маятника.

Точка подвеса и центр качания обладают свойством взаимности. Можно показать, используя теорему Штейнера, что при переносе точки подвеса в центр качания О’ период колебаний не изменится, поскольку прежняя точка подвеса становится новым центром качания О’.

Математический маятник можно представить как частный (предельный) случай физического маятника, вся масса которого сосредоточена

в его центре масс. Действительно, при этом / = ml 2 и, следовательно, со-

гласно выражению (7.17), Т — 2л. — , что совпадает с формулой (7.15).

Содержание

Лекция №7. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
5.1. Свободные гармонические колебания и их характеристики.
5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.
5.3. Дифференциальное уравнение гармонических колебаний и его решение.
5.4. Энергия гармонических колебаний.
5.5. Пружинный, математический и физический маятники.
Гармонический осциллятор.
💥 Видео

Видео:Урок 327. Гармонические колебанияСкачать

Лекция №7. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

5.1. Свободные гармонические колебания и их характеристики.

Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени. Наиболее важными характеристиками колебания являются: смещение, амплитуда, период, частота, циклическая частота, фаза.

Простейший вид периодических колебаний − это гармонические колебания. Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид

1) Смещение x − это величина, характеризующая колебания и равная отклонению тела от положения равновесия в данный момент времени.

2) Амплитуда колебаний А − это величина, равная максимальному отклонению тела от положения равновесия.

3) Период колебаний T − это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Единица измерения [T] = 1 с .

За период система совершает одно полное колебание.

4) Частота колебаний ν − это величина, равная числу колебаний, совершаемых в единицу времени (за 1 секунду). Единица измерения [ν]= 1 Гц . Частота определяется по формуле

5) Циклическая частота ω − это величина, равная числу полных колебаний, совершающихся за 2π секунд. За единицу циклической частоты принята угловая частота, при которой за время 1 с совершается 2π циклов колебаний, [ω]= с -1 . Циклическая частота связана с периодом и частотой колебаний соотношением

6) Фаза колебаний ωt + φ₀ − фаза указывает местоположение колеблющейся точки в данный момент времени.

7) Начальная фаза φ₀ − указывает местоположение колеблющейся точки в момент времени t = 0 .

5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.

Сложение нескольких колебаний одинакового направления можно изображать графически с помощью метода векторной диаграммы.

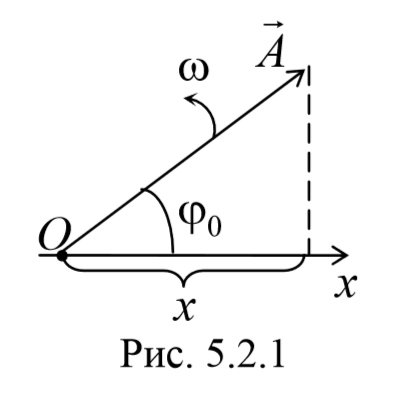
Гармоническое колебание может быть представлено графически с помощью вращающегося вектора амплитуды А . Для этого из произвольной точки O , выбранной на оси Ox , под углом φ₀ , равным начальной фазе колебания, откладывается вектор амплитуды А . Модуль этого вектора равен амплитуде рассматриваемого колебания. Если этот вектор привести во вращение с угловой скоростью ω , равной циклической частоте колебаний, то проекция конца вектора амплитуды будет перемещаться по оси Ox и принимать значения от -A до +A , а колеблющаяся величина изменяться со временем по закону x = Acos(ωt + φ₀)

1. Сложение одинаково направленных гармонических колебаний.

Сложим два гармонических колебания одинакового направления и одинаковой частоты. Смещение x колеблющегося тела будет суммой смещений x₁ и x₂ , которые запишутся следующим образом:

Представим оба колебания на векторной диаграмме. Построим по правилу сложения векторов результирующий вектор А . Проекция этого вектора на ось Ox равна сумме проекций слагаемых векторов x=x₂+x₂ , следовательно, вектор А представляет собой результирующее колебание. Определим результирующий вектор амплитуды А потеореме косинусов

Так как угол между векторами А ₁ и А ₂ равен φ=π-(φ₂-φ₁) , то cos[π-(φ₂-φ₁)]=-cos(φ₂-φ₁) , следовательно, результирующая амплитуда колебания будет равна

Определим начальную фазу результирующего колебания.

Из рисунка видно, что начальная фаза результирующего колебания

Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, также совершает гармонические колебания в том же направлении и с той же частотой.

2. Сложение взаимно перпендикулярных гармонических колебаний.

Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты, происходящих во взаимно перпендикулярных направлениях. Допустим, что материальная точка совершает колебания как вдоль оси X , так и вдоль оси Y . Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний примут вид

где φ − разность фаз обоих колебаний.

Уравнение траектории получим, исключив из уравнений (5.2.6) параметр времени t: cosωt= $$xover A_1$$ , а sinωt= $$sqrt=sqrt$$ Разложим косинус во втором из уравнений (5.2.6)

Перепишем это уравнение в следующем виде

После преобразования, получим

Используя тригонометрическое тождество cos 2 φ+sin 2 φ=1 , окончательно получим

Это есть уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно. Ориентация эллипса и величина его полуосей зависят от амплитуд колебаний и разности фаз.

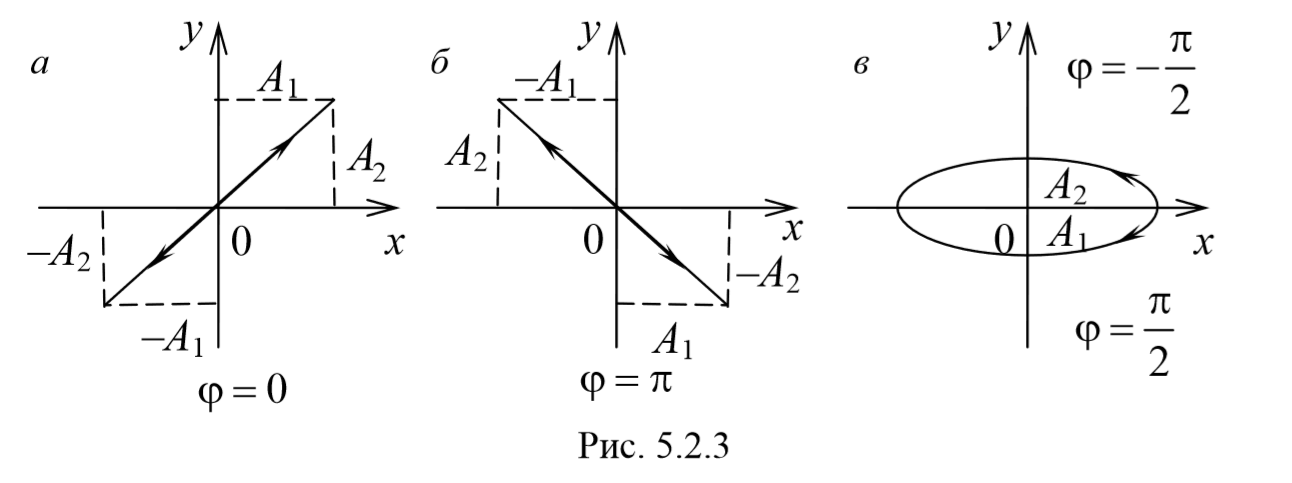
Рассмотрим несколько частных случаев и определим форму траектории для них:

a) разность фаз равна нулю [φ=0]

В этом случае $$( — )^2=0$$ , откуда получается уравнение прямой

Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой $$A= sqrt<A_1+A_2>$$ .

2) разность фаз равна ±π[φ=±π] .

В этом случае $$( — )^2=0$$ , откуда получается уравнение прямой

3) Разность фаз равна ± $$πover 2$$ [φ=± $$π over2$$ ] . Тогда

Уравнение эллипса, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд колебаний эллипс вырождается в окружность. Случаи φ=+ $$πover 2$$ и φ=- $$πover 2$$ отличаются направлением движения. Если φ=+ $$πover 2$$ , то уравнения колебаний имеют следующий вид: x=A₁cosωt , и y=-A₂sinωt и движение совершается по часовой стрелке. Если φ=- $$πover 2$$ , , то уравнения колебаний имеют следующий вид: x=A₁cosωt , и y=A₂sinωt и движение совершается против часовой стрелке.

Рассмотренные три частных случая представлены на рис. 5.2.3, а, б, в. Рис

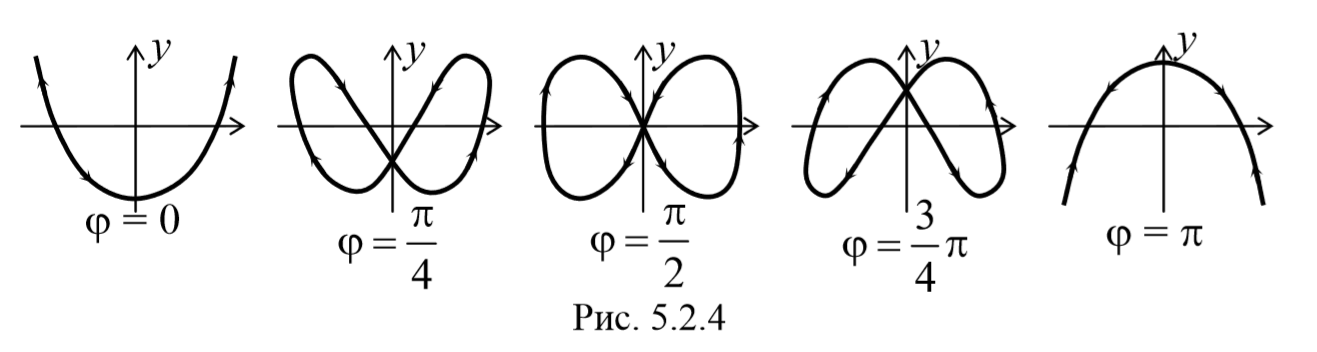
4) Если частоты складываемых взаимно перпендикулярных колебаний различны, то траектория результирующего движения имеет вид сложных кривых, называемых фигурами Лиссажу . Форма этих кривых определяется соотношением амплитуд, частот и разности фаз складываемых колебаний.

На рис. 5.2.4 показаны фигуры Лиссажу, которые получаются при соотношении частот 1:2 и различной разности фаз колебаний.

По виду фигур можно определить неизвестную частоту по известной частоте или определить соотношение частот складываемых колебаний.

5.3. Дифференциальное уравнение гармонических колебаний и его решение.

Продифференцируем по времени уравнение гармонических колебаний

и получим выражение для скорости

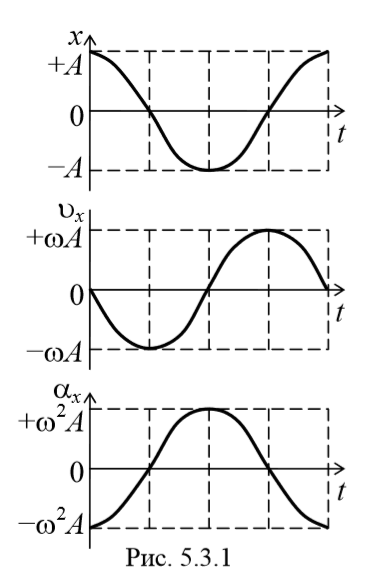
Из сравнения уравнений (5.3.1) и (5.3.2) следует, что скорость опережает смещение по фазе на π/2 . Амплитуда скорости равна Аω .

Продифференцировав уравнение (2) еще раз по времени, получим выражение для ускорения

Как следует из уравнения (5.3.3), ускорение и смещение находятся в противофазе. Это означает, что в тот момент времени, когда смещение достигает наибольшего, положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот. Амплитуда ускорения равна Аω 2 (рис. 5.3.1).

Из выражения (5.3.3) следует дифференциальное уравнение гармонических колебаний

Результирующая сила, действующая на материальную точку массой m , определяется с помощью второго закона Ньютона. Проекция этой силы

Эта сила пропорциональна смещению точки из положения равновесия и направлена в сторону противоположную этому смещению, т. е. она стремится вернуть точку в положение равновесия, и поэтому называется возвращающей силой . Таким образом, гармонические колебания происходят под действием силы F , пропорциональной смещению x и направленной к положению равновесия,

где k=mω 2 − постоянный коэффициент. Возвращающая сила подобна упругим силам, возникающим в телах при их деформации. Такая зависимость силы от смещения характерна для упругой силы, поэтому силы иной физической природы, удовлетворяющие зависимости (5.3.6) называются квазиупругими силами .

Материальная точка, совершающая колебания под действием квазиупругой силы, называется линейным осциллятором . Ее динамическое поведение описывается дифференциальным уравнением

ω₀ − собственная частота осциллятора.

Решение этого уравнения дает закон движения линейного осциллятора x=Acos(ωt+φ₀) .

5.4. Энергия гармонических колебаний.

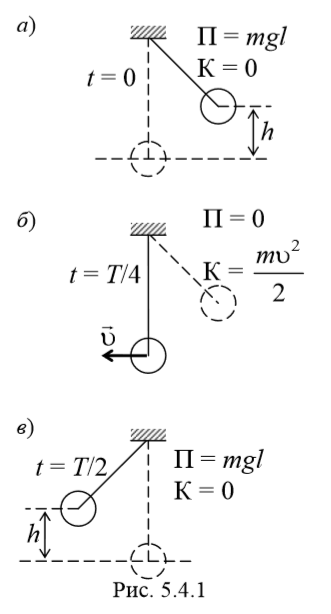
В процессе колебаний происходит превращение кинетической энергии в потенциальную энергию и обратно (рис. 5.4.1). В момент наибольшего отклонения от положения равновесия полная энергия состоит только из потенциальной энергии, которая достигает своего наибольшего значения. Далее при движении к положению равновесия потенциальная энергия уменьшается, при этом кинетическая энергия возрастает. При прохождении через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в этот момент достигает своего наибольшего значения. Далее при движении к точке наибольшего отклонения происходит уменьшение кинетической и увеличение потенциальной энергии. И при наибольшем отклонении потенциальная опять максимальная, а кинетическая энергия рана нулю. И т. д.

Потенциальная энергия тела, совершающего гармонические колебания равна

Кинетическая энергия тела, совершающего гармонические колебания равна

Таким образом, полная энергия гармонического колебания, состоящая из суммы кинетической и потенциальной энергий, определяется следующим образом

Следовательно, полная энергия гармонического колебания

оказывается постоянной в случае гармонических колебаний.

Найдем среднее значение потенциальной энергии за период колебания

Аналогично получается для среднего значение кинетической энергии

Таким образом, и потенциальная, и кинетическая энергии изменяются относительно своих средних значений по гармоническому закону с частотой 2ω и амплитудой ωt kA 2

5.5. Пружинный, математический и физический маятники.

Рассмотрим несколько простейших систем, совершающих свободные гармонические колебания.

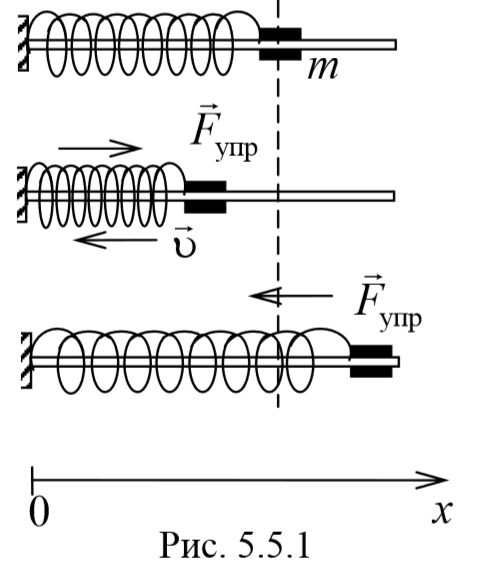
1) Пружинный маятник − это материальная точка массой m , подвешенная (или расположенная горизонтально) на абсолютно упругой пружине жесткостью k и совершающий гармонические колебания под действием упругой силы. Пусть шайба массой m , прикрепленная к пружине, совершает колебания. Для составления дифференциального уравнения колебаний запишем второй закон Ньютона в проекции на ось Ox F_упр=ma . Упругая сила F_упр=-kx . Приравнивая последние два уравнения и, используя определение ускорения тела, получим

Сравнивая уравнения (5.3.7) и (5.5.2) получаем, что пружинный маятник совершает гармонические колебания с частотой

Так как период колебаний определяется по формуле T= $$2πover ω_0$$ , то период колебаний пружинного маятника

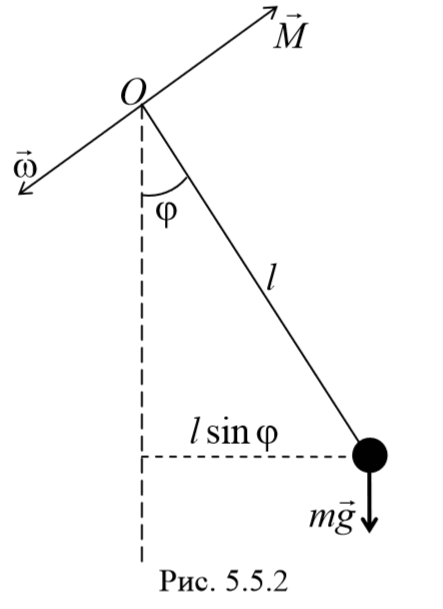
2) Математический маятник − это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена материальная точка массой m . Отклонение маятника от положения равновесия будем характеризовать углом φ , образованным нитью с вертикалью.

При отклонении маятника от положения равновесия возникает вращательный момент M , равный по величине mqlsinφ .Он имее акое же направление, что стремится вернуть маятник в положение равновесия. Следовательно, выражение для вращательного момента имеет вид: M=-mqlsinφ . Применим основно ательного движения

где L=ml 2 − момент инерции материальной точки. Тогда, учитывая, что угловое ускорение ε= $$d^2φover dt^2$$ , получим

Если рассматривать малые колебания, то sinφ≈φ . Получим

То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой

Период колебаний математического маятника

3) Физический маятник − это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через точку, не совпадающую с центром масс тела. При отклонении маятника от положения равновесия на угол φ возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен M=-mglsinφ .

Согласно основному уравнению динамики вращательного движения получаем

где I − момент инерции маятника относительно оси, проходящей через точку подвеса.

Если рассматривать малые колебания, то sinφ≈φ . Получим

Период колебаний математического маятника

Из сопоставления формул периодов колебаний математического и физического маятников T=2π $$sqrt$$ и T=2π $$sqrt$$ получается, что математический маятник с длиной

будет иметь такой же период колебаний, что и данный физический маятник.

Величина l_пр (отрезок OO′) называется приведенной длиной физического маятника − это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, и лежащая на расстоянии приведенной длины от оси вращения, называется центром качания (О′) физического маятника. Точка подвеса О и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Гармонический осциллятор.

Пружинный, физический и математический маятники.

Материальную точку, совершающую колебания, называют осциллятором (от английского слова oscillation — колебание).

Таким образом, рассмотренные выше колебания представляют собой частные случаи свободных колебаний гармонического осциллятора:

, (15.3.1)

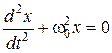
решение, которого будем записывать в виде:

где A– амплитуда колебаний; ω₀ – собственная частота; величина ω₀t+a–фаза колебания.

Примерами гармонического осциллятора являются пружинный, физический и математический маятники.

1. Пружинный маятник.

Гармонический осциллятор дифференциальное уравнение и его решение математический маятник

Пружинным маятником называется система, состоящая из груза массы m, подвешенного на пружине и совершающий гармонические колебания под действием упругой силы (рис.15.1).

Обозначим смещение пружины из положения равновесия x. Тогда сила, возникающая в пружине при выведении шарика из положения равновесия, будет равна

Эта сила пропорциональна величине смещения и направлена к положению равновесия. В таком случае уравнение движения шарика, согласно второму закону Ньютона, запишется в виде

Обозначив , перепишем уравнение движения пружинного маятника:

. (15.3.2)

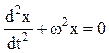
Из уравнения (15.3.2) следует, что движение пружинного маятника описывается линейным однородным дифференциальным уравнением второго порядка.

Решение уравнения (15.3.2) имеет вид

где 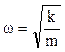— частота гармонических колебаний.

Тогда 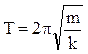— период колебаний пружинного маятника.

2. Физический маятник

Твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции называется физическим маятником (рис.15.2).

Покажем, что и физический маятник будет совершать гармонические колебания.

В положении равновесия центр инерции маятника (С) находится под точкой подвеса (О) на одной с ней вертикали.

При отклонении маятника от положения равновесия на угол j возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен произведению силы тяжести на плечо силы (d):

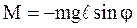
где — расстояние между центром инерции и точкой подвеса.

Согласно основному уравнению динамики вращательного движения, вращательный момент равен

. (15.3.4)

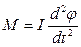
В случае малых колебаний sinj

j и, приравнивая (15.3.3) и (15.3.4), получим уравнение колебаний физического маятника:

. (15.3.5)

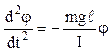
и перепишем уравнение (15.3.5) в виде

. (15.3.6)

Уравнение колебаний физического маятника (15.3.6) представляет собой однородное линейное дифференциальное уравнение второго порядка.

Из теории дифференциальных уравнений известно, что решением уравнения (15.3.6) будет функция вида

т.е. при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота и период которых определяются из следующих соотношений:

;

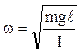
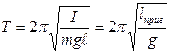
где — приведенная длина физического маятника (на рис. 15.2 приведенная длина соответствует отрезку ОО / ). Точка О / на продолжении прямой ОС, отстоящей от точки О подвеса маятника на расстоянии приведенной длины, называется центром качаний физического маятника.

Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

3. Математический маятник

Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешено тело точечной массы m и совершающей колебания под действием силы тяжести.

Приближенно можно считать математическим маятником небольшой, нетяжелый шарик, подвешенный на тонкой длинной нити (рис.15.3).

Отклоним маятник от положения равновесия на угол a и предоставим ему возможность совершать колебания.

На маятник в отклоненном состоянии действует возвращающая сила

Она направлена по касательной к траектории движения шарика в сторону положения равновесия. Согласно второму закону Ньютона, уравнение движения математического маятника запишется в виде

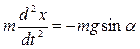
В общем случае решение уравнения сложно.

Рассмотрим случай, когда отклонение маятника от положения равновесия настолько малы, что синус угла можно считать пропорциональным величине угла:

Тогда смещение по дуге приближенно можно считать равным смещению вдоль горизонтальной хорды и синус угла a заменить отношением смещения x к длине нити

(15.3.7)

и подставляя его в уравнение (15.3.7), получим уравнение движения математического маятника:

(15.3.8)

Из вида уравнения (15.3.8) следует, что движение математического маятника описывается линейным однородным дифференциальным уравнением второго порядка.

Из теории дифференциальных уравнений известно, что решением уравнения (15.3.8) является функция вида

т.е. математический маятник совершает гармонические колебания с частотой

Таким образом, период колебаний математического маятника зависит только от ускорения силы тяжести в данном месте Земли и от длины маятника.

Математический маятник представляет собой частный случай физического маятника, где вся масса твердого тела сосредоточена в одной точке, находящейся на постоянном расстоянии от точки вращения.