Функция выручки — зависимость между количеством производимого блага и величиной денежной суммы, получаемой от продажи товара. Функция выручки выводится из спроса:
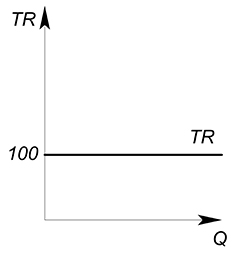
Функции выручки могут иметь совершенно разнообразный вид:
Пример 1
Функция спроса описывается зависимостью $Q(P)=dfrac $. Найти функцию выручки.
Выразим обратную функцию спроса: $P(Q)=dfrac$; теперь найдем функцию выручки: $TR=dfrac
cdot Q=100$. В данном случае выручка постоянна, не зависит от количества производимого блага и равна 100.
Подробнее о функции выручки мы будем говорить, когда будем изучать рыночные структуры.
Определение 2
Средняя выручка (AR — average revenue) показывает, какую выручку в среднем приносит единица продаваемого товара:
$AR=dfrac
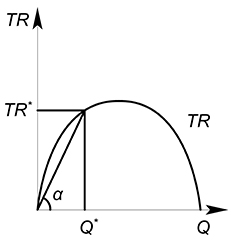
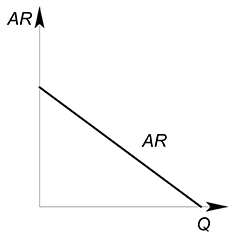
$Геометрический смысл средней выручки — тангенс угла наклона луча (секущей), проведенного из начала координат к какой-нибудь точке на графике выручки:
Проведя огромное количество лучей к графику выручки мы сможем получить график средней выручки $AR$.
Так среднюю выручку можно описать функцией, вид которой будет совпадать с обратной функцией спроса:
Определение 3
Предельная выручка (MR — marginal revenue) показывает, какую выручку принесет дополнительная произведенная единица товара.В дискретном случае предельная выручка будет равна $MR=dfrac
Геометрический смысл предельной выручки — тангенс угла наклона секущей, соединяющей точки $(Q_2;TR_2)$ и $(Q_1;TR_1)$.
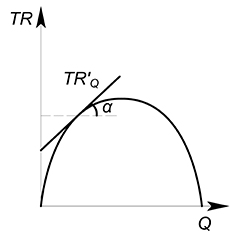
Если мы предполагаем, что производимый нами товар является бесконечно делимым, то нам будет интересно узнать какую выручку принесет дополнительная бесконечно малая единица выпускаемого блага.
Тогда геометрический смысл в данном случае будет следующий: MR есть тангенс угла наклона касательной, проведенной к графику функции выручки в интересующей нас точке.
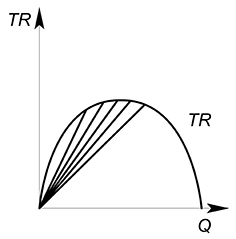
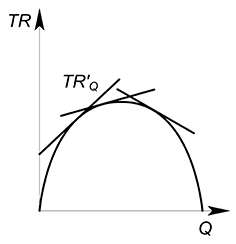
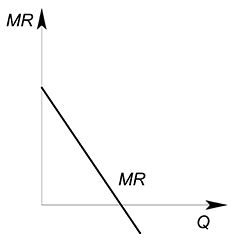
Проведя множество касательных к разным точкам сможем построить функцию предельной выручки:
В данном случае предельная выручка будет производной функции выручки: $MR(Q)=TR'(Q)$.
Пример 2
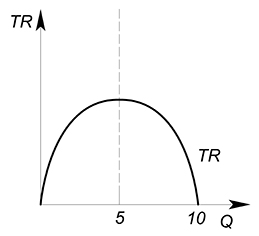
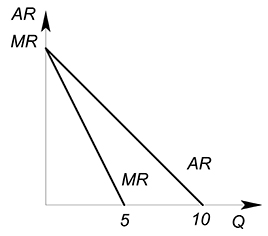
Функция спроса описывается уравнением $Q(P)=10-P$. Найти функции TR, AR, MR и изобразить их графики.
Выразим обратную функцию спроса: $P(Q)=10-Q$. Теперь найдем функцию выручки: $TR(Q)=P(Q)cdot Q=10Q-Q^2$. Можно найти функции средней и предельной выручки: $AR(Q)=dfrac
Максимизация функции выручки выполняется так же, как и любой другой функции — можно использовать производную (подробнее о максимизации функции можете узнать здесь), а можно обойтись без нее (подробнее здесь)
Пример 3
Обратная функция спроса имеет вид: $P(Q)=20-2Q$. Найти максимальную выручку.Запишем функцию выручки: $TR=20Q-2Q^2$. Это парабола, ветви вниз. Найдем точку максимума: $x_0=-dfrac=dfrac=5$. Подставим данную точку в функцию выручки: $TR=20cdot 5-2cdot 25=100-50=50$.
Также для функции $AR$ $TR$ в точке будет является произведением значений координат на осях:
для $MR$ — $TR$ в точке есть площадь под графиком функции, слева ограниченная осью $P$, справа перпендикуляром к оси $Q$, проведенным из интересующей нас точки:
СодержаниеВидео:Функция потребленияСкачать
Функция спроса Qd=12-2Р. Найдите: а) формулу зависимости выручки продавцов от цены товара; б) максимальную выручку продавцов
Готовое решение: Заказ №10007
Тип работы: Задача
Статус: Выполнен (Зачтена преподавателем ВУЗа)
Предмет: Экономика
Дата выполнения: 06.11.2020
Цена: 229 руб.
Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
Функция спроса Qd =12-2Р. Найдите:
а) формулу зависимости выручки продавцов от цены товара;
б) максимальную выручку продавцов;
в) цену, при которой выручка продавцов равна 10;
г) формулу зависимости выручки продавцов от объема продаж;
д) выручку продавцов при объеме продаж 4.
Решение:
а) Найдем формулу зависимости выручки продавцов от цены товара:
TR = P * Q = P (12-2 P )=12 P -2 P 2
б) Рассчитаем максимальную выручку продавцов:
TR мах = 12 P -2 P 2 =12*3-2*3 2 =18 д.е.
Максимальная выручка продавцов составляет 18 д.е.
Изучите экономику на странице ➔ решение заданий и задач по экономике.
Похожие готовые решения:
- Оцените следующую экономическую ситуацию! Предприниматель Михаил владеет небольшой фирмой по выращиванию цветов «Одуванчик». Он нанимает трех помощников за 10 тыс.у.е. в год
- Рассчитайте величины постоянных и переменных издержек на основе следующих данных: сырье и материалы – 5 тыс. долл., амортизация: станков – 4 тыс. долл., зданий – 8 тыс. долл.
- Кривые спроса и предложения на рынке аудиокассет представлены соответственно выражениями Р=42-Qd и Р=2Qs. Предположим, государство облагает продавцов кассет налогом равным 21 ден.ед.
- На рынке конкретного товара известны функция спроса Qd=8-Р и функция Qs=-7+2Р. Производители товара получают субсидию в размере 1,5 долл. на ед. товара
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Функция сбереженийСкачать
Типовые задачи с решениями
1. Функция спроса на товар QD = 18 — 2Р, функция предложения товара Qs = -3 + Р. Какую максимальную сумму акциза можно собрать с данного рынка?
При введении акциза равновесие на рынке приобретает вид
Сумма собранного акциза Т = tQ = At — 2/’it 1 . Она достигает максимума при 4 — 4/31 = 0 => t = 3. Тогда Т = 6.
2. Спрос и предложение описываются уравнениями QD = = 2400 — 100Р Qs = 1000 + 250Р. Найти равновесную цену и равновесный объем продаж.
В состоянии равновесия
3. (Пункция спроса населения на данный товар QD = 8 — Р, функция предложения данного товара Qs — -7 + 2Р. Определить излишек покупателя и продавца.
Определяем равновесную цену и равновесный объем продаж:
Максимальная цена спроса 8-Р=0=>Р=8. Излишек покупателя (8 — 5) • 3/2 = 4,5.
Максимальная цена предложения -7 + 2Р = 0 => Р = 3,5. Излишек продавца (5 — 3,5) • 3/2 = 2,25.
4. Функция спроса на товар QD = 9 — Р, функция предложения Qs= -6 + 2Р. Предположим, что на данный товар введен потовар- ный налог, уплачиваемый продавцом, размером 1,5 руб. за единицу.
Определить цену продавца, цену покупателя и равновесный объем продаж после введения налога.
После введения налога условие равновесия будет иметь вид
где Р’ — цена покупателя; Р — цена продавца.
5. Функция спроса на товар QD = 16 — АР, функция предложения Qs = -2 + 2Р. Определить ставку налога, при которой равновесный объем продаж составит две единицы.
При введении налога цепа покупателя (Р + ) будет равна
цена продавца:
Следовательно, ставка налога t = 3,5 — 2 = 1,5.
Видео:Конформные отображенияСкачать
Задачи для самостоятельного решения
1. Функция спроса на данный товар имеет вид Qj = 12 — Р, функция предложения Qs = -3 + 4Р.
Определите равновесную цену и объем продаж. Введен акциз на продукцию в размере 20% от цены покупателя. Определите новые равновесные объем продаж и цену. Какую величину налогового сбора получит государство?
2. Функция спроса па данный товар имеет вид Q,t = 2 — 3Р, функция предложения Qs = -0,5 + 2Р.
Определите общественную выгоду (сумму излишков покупателей и продавцов) по рыночным ценам.
3. Функция спроса на товар имеет вид Qj = 5 — Р, функция предложения товара Q s = -1 + 2Р. Предположим, что установлена квота па производство данного товара в размере двух единицы.
Рассчитать излишки продавца и покупателя до и после введения квоты.
4. Функция спроса на некоторый товар имеет вид QDr = 150 — Р,. Функция предложения данного товара Qs, = -15 + 0,5Р,, гдеР, — цена товара в период t, которую ожидают производители в момент принятия решений об объемах производства. Предположим, что
Pt-Pt-1а) Определить объемы продаж и цены данного товара в периоды 1, 2, 3, 4, если известно, что Р0 = 100.
- б) Определить равновесную цепу н равновесный объем продаж.
- в) Можно ли равновесие назвать стабильным?
Видео:Вышмат. Сопряжённое пространство. Дифференцируемые отображения нормированных пространствСкачать
Алгоритм решения задач D — S
Алгоритм решения задач D — S
Вот предложенный Интернетом алгоритм решения конкретной задачи. Он полезен как обобщающий пример. Но с необходимыми дополнениями и изменениями.
http://www.semestr.ru/ks296Из темы о спросе и предложении необходимо помнить, что при ПРУ (прочих равных условиях):
-увеличение объёма спроса вызывает рост как величины равновесной цены Ре (Рравн), так и равновесного значения Qе
(Qравн. На графиках авторов Ре и Qе не используются) ;
— сужение спроса приводит к уменьшению и Ре, и Qе;
— повышение объёма предложения способствует возрастанию Qе и снижению Ре (если сохраняется спрос на данные товары и услуги);
— сокращение предложения обусловит падение Qе и рост Ре;
— по закону спроса изменение Qe обратно пропорционально изменению Ре;
— по закону предложения изменение Qe прямо пропорционально изменению Ре
(у авторов в случае изменения спроса, величины Ре и Qe изменяются в одном направлении…);
— при росте спроса и росте предложения увеличивается Qe с разными вариациями Ре (возможно и сохранение прежней цены равновесия);
— при росте спроса и снижении предложения снижается Qe и увеличивается Ре;
— при снижении спроса и росте предложения снижаются Qe и Ре
(у авторов любопытная формула — Если произойдет одновременное изменение и спроса, и предложения, то величины равновесных Ре и Qе определяются в каждом конкретном случае степенью изменения спроса и предложения).Отсюда необходимые дополнения к графику авторов.
Pmax ; максимальной цене за 1 (единицу) товара, хотя на графике точка указывается на 0.
(выше Pmax потребитель покупать при ПРУ товар не будет).
Pmin; минимальной цене за 1 (единицу) товара, хотя на графике точка указывается на 0 (ниже Pmin производитель продавать товар не будет).Теперь алгоритм решения конкретной задачи.
Задан равновесный объем, когда:
— функция спроса на данный товар:
Qd = 40 — 2P; отсюда если приравнивать к нулю сразу 2Р = 40, а Р = 20 (; Pmax).
функция предложения:
Qs = -26 + 4Р; откуда если приравнивать к нулю сразу 26 = 4Р, а Р = 6,5 (; Pmin)..Требуется последовательно:
— построить кривые спроса и предложения;
— определить равновесную цену, равновесный объем продаж;
— найти коэффициент эластичности спроса и предложения в точке равновесия;
— излишек потребителя, излишек производителя;
— определить максимальную цену, по которой может быть куплена первая единица изделия;
— описать последствия принятия государством решения о фиксации цены на 1 ед. выше равновесной;
— описать последствия принятия государством решения о фиксации цены на 1 ед. ниже равновесной;
— показать графически, что потеряют покупатели и производители при установлении государством налога с продажи на единицу данного товара в размере 2 ден. единицы.
— описать последствия введения субсидии государством за каждый проданный товар в размере 2 руб.;
— найти максимальную выручку при равновесной цене.1) построим кривые спроса и предложения по образцу графика А;
2) Определим равновесную цену, равновесный объем продаж.
В точке равновесия E объем спроса Qs равен объему предложения Qd (d малое D, спрос и объём спроса).
Qd = Qs40 — 2P = -26 + 4P (цикл привычных математических преобразований 66 = 6P или)
6P = 66
Pравн = 11 — равновесная цена
Qравн = Qd = Qs = -26 + 4*11 = 40 — 2*11 = 18 шт. — равновесный объем продажИзлишек потребителя (или выигрыш) — это разность объёмов спроса между максимальной ценой, которую он готов отдать за товар ; Pmax, и той, которую он действительно платит. Pе.
Излишек производителя (выигрыш) — эта разность объёмов предложения между рыночной ценой и той минимальной ценой ; Pmin, за которую производители готовы продать свой товар.
Излишек (площадь треугольника) продавца: (Pравн — Ps)Qравн / 2 = (11 — 6,5) * 18/2 = 40,5;
Излишек (площадь треугольника) покупателя: (Pd — Pравн)Qравн /2 = (20 — 11) * 18/2 = 81.Qd = 0; 40 — 2P = 0; Pd (; Pmax; максимальная цена спроса) = 20;
Qs = 0;-26 + 4Р = 0; Ps (; Pmin; минимальная цена предложения) = 6,53) определим максимальную цену, по которой может быть куплена первая единица изделия (по графикам максимальные и минимальные цены приравниваются к нулевым объемам, хотя в реальности – к единице; здесь несовпадение математики и экономики);
Находим максимальную цену, по которой потребитель приобретет первую единицу товара через приравнивание Qd к нулю:
Qd=0
40 — 2P = 0
Р = 204) описать последствия принятия государством решения о фиксации цены на 1 ед. выше равновесной;
Pфикс = Pравн + 1 = 11 + 1= 12
Объем спроса Qdфикс = 40 — 2P = 40 — 2*12= 16 шт.
Объем предложения Qsфикс = -26 + 4P = -26 + 4*12 = 22 шт.
После фиксации цены, объем спроса уменьшился на 2 шт. (18 — 16), а излишек производителей увеличился на 4 шт. (22 — 18). На рынке излишек товаров в размере 6 шт. (22 — 16).5) описать последствия принятия государством решения о фиксации цены на 1 ед. ниже равновесной;
Pфикс = Pравн — 1 = 11 — 1= 10
Объем спроса Qdфикс = 40 — 2P = 40 — 2*10= 20 шт.
Объем предложения Qsфикс = -26 + 4P = -26 + 4*10 = 14 шт.
После фиксации цены, объем спроса увеличился на 2 шт. (18 — 20), а предложение сократилось на 2 шт. (18 — 16). На рынке дефицит товаров в размере 6 шт. (20 — 14).6) показать графически, что потеряют покупатели и производители при установлении государством налога с продажи на единицу данного товара в размере 2 ден. единицы.
Сдвиг кривой предложения вверх, влево.Налог = SP0P2E2M1
Для нахождения новой равновесной цены при введении налога с продажи изменяем функцию предложения Qsналог = -26 + 4(P — 2), оставляя без изменения функцию спроса, а затем их приравниваем:
Qsналог = Qd
40 — 2P = -26 + 4(P — 2)
74 = 6P
Pналог = 12,3 — равновесная цена при налоге с продаж;
Qsналог = 40 — 2*12,3 = 15,3В результате излишек потребителей и производителей сократится на величину площади, соответствующей SPPнE2E и SPP0ME
Излишек продавца: (P0 — Psн)Qsналог / 2 = (10.3 — 6.5) * 15,3/2 = 29.1;
Излишек покупателя: (Pd — Pналог)Qsналог / 2 = (20 — 12,3) * 15,3/2 = 58,9.
15,3 = -26 + 4*P; P0 = 10,3Разделение налогового бремени между потребителями и производителями зависит от эластичности кривых спроса и предложения.
Если спрос эластичен налоговое бремя ложится на производителя.
Если спрос неэластичен, налоговое бремя несет преимущественно потребитель.
При эластичном предложении налоговое бремя ляжет в основном на потребителя.
При неэластичном предложении налоговое бремя ляжет на производителя.
Доля продавца в новой цене ;Рпрод = Pравн — Psн = 11 — 10,3 = 0,7
Доля покупателя в новой цене ;Рпокуп = Pналог — Pравн = 12,3 — 11 = 1,3
Сумма налоговых поступлений в бюджет: (Pналог — Psн)Qsналог = (12,3 — 10,3)*15,3 = 30,6
Чистые потери от введения налога (чистые потери благосостояния): (12,3-11)*(18-15,3)/2 + (11-10,3)*(18-15,3)/2 = 1,8 + 0,9 = 2,77) При введении субсидии государством за каждый проданный товар в размере 2 руб.
Qsсубсидия = -26 + 4(P + 2) = -18 + 4Р
Сдвиг кривой предложения вправо. Субсидирование всегда сопровождается чистыми потерями для общества.
Новая равновесная цена при дотации
40 — 2Р = -18 + 4Р
58 = 6Р
Рсубсидия = 9,7 — равновесная цена при дотации товаров
Qсубсидия = 40 — 2*9,7 = 20,7 — равновесный объем продаж при субсидировании товаров
20,7 = -26 + 4*P; P = 11,7
Доля продавца ;Рпрод = 11,7 — 11 = 0,7
Доля покупателя ;Рпокуп= 11 — 9,7 = 1,3
Объем средств, необходимый для субсидирования:
V = ;Q*;Рпрод = (20,7 — 18)*(9,7-11) = 3,58) Максимальная выручка при равновесной цене
W = Q*P = 18*11 = 198
При цене р > р* объем продаж и выручка определяется функцией спроса, при р < р* — предложения. Необходимо найти цену р, определяющую максимум выручки:
При р*(40 — 2р) максимум достигается в точке р* = 10 (определяем максимум через производную, 40 — 4р = 0 ), выручка W(10) = 10*20 = 200
Таким образом, максимальная выручка W(p) = 200 достигается не при равновесной цене.9) Найдем коэффициент прямой эластичности спроса и предложения в точке равновесия.
Коэффициент прямой эластичности спроса в точке равновесия.
Функция спроса: Qd = 40 — 2P
Коэффициент наклона прямой спроса: -2.
Pравн = 11 — равновесная цена
Qравн = Qd = Qs = 18 — равновесный объем продаж
Е = -2*11/8 = -2,75Коэффициент прямой эластичности предложения в точке равновесия.
Функция предложения: Qs = -26 + 4Р
Коэффициент наклона прямой предложения: 4.
Е = 4*11/8 = 5,5Эти упражнения сравнительно простые и неплохо готовят к официальным тестированиям по «Экономике» и «Экономической теории».
📹 Видео
Химия (8 класс) - Приёмы обращения с лабораторным оборудованием. Наблюдение за горящей свечой...Скачать
21 функция полезности Кобба Дугласа и квазилинейная функция полезностиСкачать
ЕГЭ информатика задание 14. "Позиционные системы счисления"Скачать
Теория потребителя. Функция Кобба-ДугласаСкачать
Работа с FireSec. 20. Мультисерверная задачаСкачать
Запас по амплитуде/фазе и полоса пропускания - часть 12 (неустойчивость часть 2)Скачать
Методы оптимизации 9 Двойственность Сопряженные функцииСкачать
Построение производственной функции Кобба-ДугласаСкачать
15 Функция полезности определениеСкачать
СкважностьСкачать
MAGNET Field Расчеты – ХодСкачать
2020.04.21 В.А. Александров «Оптимизация размещения полюсов в одномерной системе управления»Скачать
Совокупности их Параметры и Статистики за 8 минутСкачать
Лекция 268. Источник питания на повторителеСкачать
Сортировка массива подсчетомСкачать


 Определение 3
Определение 3 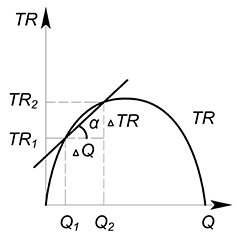
 Максимизация функции выручки выполняется так же, как и любой другой функции — можно использовать производную (подробнее о максимизации функции можете узнать здесь), а можно обойтись без нее (подробнее здесь)
Максимизация функции выручки выполняется так же, как и любой другой функции — можно использовать производную (подробнее о максимизации функции можете узнать здесь), а можно обойтись без нее (подробнее здесь)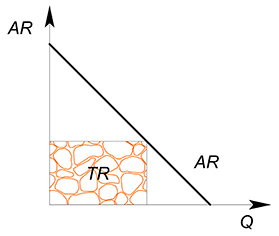

 Готовое решение: Заказ №10007
Готовое решение: Заказ №10007
 Тип работы: Задача
Тип работы: Задача
 Статус: Выполнен (Зачтена преподавателем ВУЗа)
Статус: Выполнен (Зачтена преподавателем ВУЗа)
 Предмет: Экономика
Предмет: Экономика
 Дата выполнения: 06.11.2020
Дата выполнения: 06.11.2020
 Цена: 229 руб.
Цена: 229 руб.









 где Р’ — цена покупателя; Р — цена продавца.
где Р’ — цена покупателя; Р — цена продавца.
 цена продавца:
цена продавца: