Функция совокупной полезности товара задана уравнением (7 видео)

Примеры решений задач: функция полезности

В этом разделе вы найдете подробно решенные задачи, касающиеся функции полезности, задачи выбора потребителем набора благ при заданном бюджетном ограничении, максимизации полезности, заменяемости товаров и т.д.

Содержание

Функция полезности: задачи с решениями
2.6 Бюджетное ограничение и полезность
Функция совокупной полезности потребителя от потребления благ А и В заданы уравнениями TUa=16Qa-Qa2 ; TUb=20Qb-1,5Qb2. Цена блага А (Ра) равна 2, цена блага В (Рb) равна 5.
Описание и исходные данные задания, 50% решения + фотография:
🔍 Видео

Видео:Предельная полезностьСкачать

Функция полезности: задачи с решениями

Задача 1. Функция полезности имеет вид: $TU=4xy$, где X и Y — количество товаров. Расходы потребителя на эти два товара в месяц равны 1200 р., цена товара X — 400 р., товара Y — 300 р. Определите оптимальный объем ежемесячных закупок двух данных товаров и соответствующее ему значение общей полезности.

Задача 2. Условия: потребитель расходует 200 руб. в неделю на покупку товаров А и В.
Цена (руб.) Кол-во покупаемых единиц товаров Общая полезность Предельная полезность
А 7 20 500 20
В 5 12 1000 30
Задание: Объяснить, как должен поступать потребитель, чтобы максимизировать получаемую полезность при данном бюджете.

Задача 3. Потребитель покупает три товара Х, Y, Z, цены которых соответственно равны Px=100 руб.; Py=70 руб.; Pz=50 руб. Функции общей полезности разных благ: $F(TU(x))=3sqrt$, $F(TU(y))=5sqrt$, $F(TU(z))=5sqrt$.
Определить:
1) каким образом потребитель может использовать денежный запас 500 рублей для достижения максимальной полезности при потреблении и рассчитать её количественно;
2) то же, если при покупке более, чем 2-х товаров Px снижается на 25%, а Py – на 50%

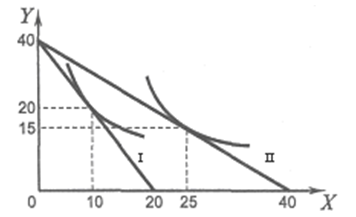
Задача 4. Допустим, потребитель имеет доход 200 ден. ед. На рисунке показаны две бюджетные линии (I и II) и соответствующие им кривые безразличия.

Определить координаты (P,Q) двух точек линии спроса данного потребителя на товар Х.

Задача 5. Общая полезность благ $alpha$ и $beta$ для некоего потребителя описывается уравнениями $U_alpha = q_alpha(15 — 0,5q_alpha)$, $U_beta = q_beta(30 — q_beta)$. Допустим, потребитель располагает бюджетом для покупки $alpha$ и $beta$ в размере 120 руб., цены на $alpha$ и $beta$ равны соответственно 5 и 10 руб. Определить количество $alpha$ и $beta$, максимизирующее полезность потребителя.

Задача 6. Потребитель тратит 7 долларов в день на товары X и Y. MU товара X для него равна $10 – x$, где $x$ — количество X в шт. MU товара Y: $21 – 2y$, где $y$ — количество Y в шт. Р 1 ед. товара X = 1 доллар, P 1 ед. Y = 1 доллар. Какое количество X и Y купит рациональный покупатель?

Задача 7. В таблице представлена предельная полезность для походов в магазин.
Имея 100 руб. 80 коп. потребитель купил 3 буханки хлеба по цене 8 руб. за буханку, 4 пакета молока по 11 руб. 20 коп. за пакет и 2 пачки сахара по 16 руб. за пачку. Достиг ли он максимума полезности? Ответ обосновать и в случае отрицательного ответа определить объем покупок, обеспечивающий максимум полезности при данном бюджете.

Задача 8. Построить кривую безразличия для двух абсолютно взаимозаменяемых товаров: пепси-колы и кока-колы, если их цены за литр равны 8 и 10 ден. ед. при бюджете на их потребление, равном 40 ден. ед.

Задача 9. Индивидуум имеет функцию полезности типа Неймана—Моргенштерна, а элементарная функция полезности строго возрастает и зависит только от одного аргумента (денег). Лотерея 6 долларов и 10 долларов с вероятностями 1/3 и 2/3 и лотерея 3 доллара и 9 долларов с вероятностями 2/3 и 1/3 для него эквивалентны. Что можно сказать о склонности данного индивида к риску?

Задача 10. Пусть функция полезности наборов из двух товаров $X=(x_1,x_2)$ имеет вид $u(x_1,x_2)=x_1^x_2^$.
• Найти набор товаров, который имеет такую же полезность, как набор $X_1=(5,3)$ и количество второго товара равно 1.
• Для набора $X_1=(5,3)$ найти предельные полезности первого и второго товаров.
• В наборе $X_1=(5,3)$ количество первого товара увеличивается на 0,1, а второго уменьшается на 0,2. Найти приближённое изменение полезности.

Задача 11. Функция полезности потребителя имеет вид $u(x_1,x_2)=(x_1-50)^(x_2-40)^$.
1. Найти равновесный спрос и его полезность, если рыночная цена первого товара $p_1=5$, рыночная цена второго товара $p_2=3$ и потребитель выделяет на приобретение товаров сумму $M=5000$ денежных единиц.
2. Найти функции спроса на оба вида товаров.
3. Найти спрос на оба товара при увеличении дохода на 30 денежных единиц и при уменьшении дохода на 60 денежных единиц.

Задача 12. Для потребителя с функцией полезности $U(x_1,x_2)=x_1^x_2^$
1) найдите функцию спроса на каждый товар;
2) найдите точку спроса при доходе $K=60$ и ценах $P=(2,4)$.

Задача 13. Решить прямую задачу потребителя (найти оптимальную потребительскую корзину). Дано: Функция полезности потребителя $U=sqrt$. Цена блага х равна 15, цена блага у равна 20, доход потребителя равен 300.
Найти: Оптимальный набор благ потребителя $(х, у)$.

Задача 14. Предельная полезность первой единицы блага равна 300. При потреблении первых трех единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза. Предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 5 раз. Найти совокупную полезность 5 единиц блага.

Видео:Как мыслит потребитель? Кривые безразличияСкачать

2.6 Бюджетное ограничение и полезность

Рассмотрим случай, когда товаров всего 2:

$I=P_xcdot+P_ycdot$
В данной формуле I обозначает доход; $P_x$, $P_y$ — цены товаров; $x$, $y$ — их количества.

Определение 2
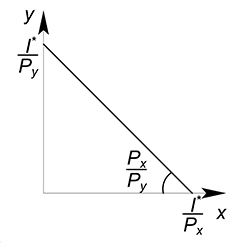
Пусть потребитель (как обычно) потребляет два товара — x и y. тогда назовем U(x, y) такое число, что чем потребителю лучше от потребления x и y, тем оно больше. если в каких-то двух наборах U совпадает, то для потребителя эти наборы эквивалентны.

Функция полезности показывает зависимость между количеством потребленного товара и полученной от потребления полезностью.

Определение 3
Кривая безразличия показывает все товарные наборы, приносящие потребителю одинаковый уровень полезности.

Пример 1
Цена товара $x$ равна 10 д.ед., цена товара $y$ составляет 5 д.ед. Доход равен 100 д.ед. Функция полезности задана уравнением $U=xy$. Найти оптимальное количество потребления двух благ.

В задачах на данную тему нам необходимо выбрать оптимальную комбинацию потребления товаров, которая будет приносить максимально возможный уровень полезности при заданном уровне дохода. Метод, используемый в задачах данного типа, похож на метод максимизации выручки

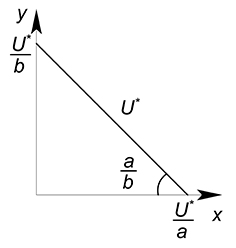
Построим график функции бюджетного ограничения.

Функция полезности задана уравнением $U=xy$. Зафиксируем переменную $U$ на некотором уровне $U^*$, получим функцию, зависящую от одной переменной $x$:

Изобразив на одном графике бюджетное ограничение и функцию полезности, начнем двигать функцию полезности вверх, пока она не достигнет максимально высокого уровня, то есть, пока прямая бюджетного ограничения не станет касательной к графику функции полезности.

Теперь приравняем производную функции бюджетного ограничения ($y'(x)=-2$) к производной кривой безразличия ($y'(x)=-dfrac$).

$x=sqrt<dfrac>$ (выбираем, естественно, положительный корень)

Мы получили оптимальные объёмы товаров $x$ и $y$ при данной функции полезности и соотношении цен товаров. Теперь найдем их числовое значение, помня про размер нашего дохода (найдем точку на прямой бюджетного ограничения, дающую максимальный уровень полезности):

Решим данное уравнение, получим максимально возможное значение полезности при данном уровне дохода:

Найдем соответствующую ему оптимальную комбинацию $x$ и $y$:

Здесь это можно также решить гораздо проще, если выразить $y$ из бюджетного ограничения и подставить в функцию полезности. Сразу же получится квадратичная парабола.

$U=x(f(x))$, где $f(x)$ — функция бюджетного ограничения.

Пример 2

Если у нас абсолютно взаимозаменяемые (для потребителя не имеет значения иметь единицу $x$ или единицу $y$, если на рынке один из товаров стоит дороже, то потребитель не будет его покупать) товары заменяются друг на друга в постоянной пропорции, вне зависимости от количества благ.

Пропорция всегда постоянна — функция полезности линейна при зафиксированном уровне $U^*$.

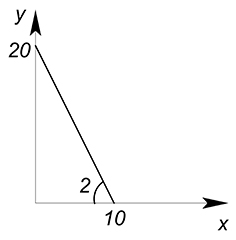
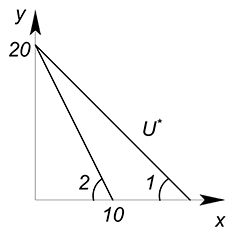
Цена товара $x$ равна 10 д.ед., цена товара $y$ составляет 5 д.ед. Доход равен 100 д.ед. Функция полезности задана уравнением $U=x+y$. Найти оптимальное количество потребления двух благ.

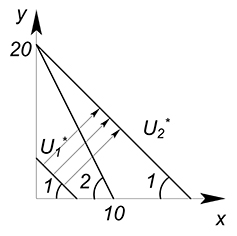
Аналогично с задачей 1 построим график функции бюджетного ограничения.

Дальше будем поступать аналогично случаю, когда КПВ у нас линейная (это ведь тоже бюджетное ограничение), и мы ищем максимально доступную выручку (сейчас максимальный уровень полезности).

Зафиксируем $U^*$, выразим $y$ через $x$:

Начнем двигать вверх данную прямую, пока она не достигнет максимально высокого положения из вcех возможных.

Получим оптимальную точку $x=0$, $y=20$, $U=20$.

Пример 3

Если товары являются взамодополняющими, функция полезности будет иметь вид:

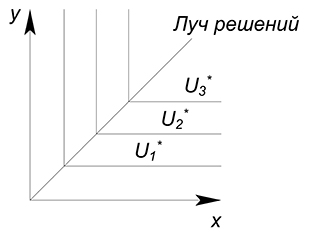
Если товары потребуются только в комплекте, то дополнительная единица одного из благ не принесет увеличения уровня полезности. Увеличение объёма только одного блага бессмысленно, ибо получить больший уровень полезности можно только при пропорциональном увеличении количества обоих благ.

В данном случае решение будет лежать на луче решений, который будет проходить через вершины углов кривых безразличия.

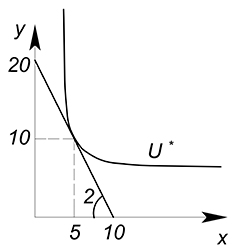
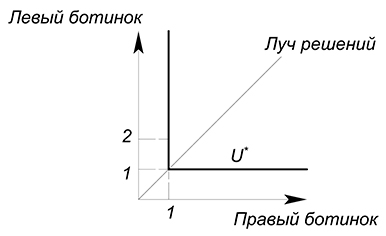
Цена товара $x$ равна 10 д.ед., цена товара $y$ составляет 5 д.ед. Доход равен 100 д.ед. Функция полезности задана уравнением $U=min(x;y)$. Найти оптимальное количество потребления двух благ.

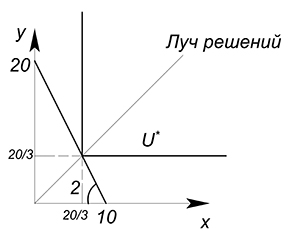
Функция полезности. Пропорция $x:y$ равна $1:1$, луч решений будет иметь вид

Нарисуем все на одном графике. Будем двигаться вверх вдоль луча решений до точки его пересечения с графиком бюджетного ограничения:

Найдем оптимальные объёмы товаров:

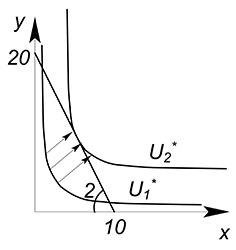
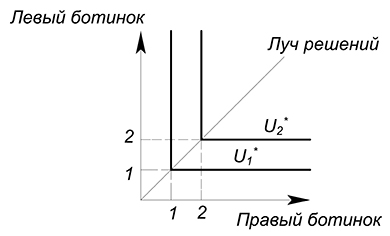
Выше мы рассмотрели случай с пропорцией потребления $1:1$. Такая пропорция подходит, например, для такого товара как ботинки. Если у нас будет 2 левых и 1 правый ботинок, то такая комбинация принесет такой же уровень полезности, как комплект из 1 правого и 1 левого ботинка (если нам доступна комбинация $2+1$, то мы не перейдем на более высокую кривую безразличия, а просто продвинемся вдоль одной из осей старой):

А комплект с пропорциональным увеличением обоих благ уже будет обладать большей полезностью:

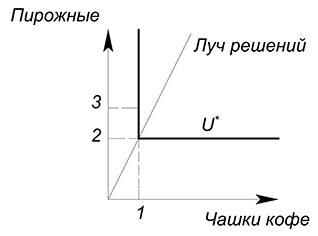
Но вообще пропорции потребления могут быть любыми. Решение тогда все равно будет лежать на луче, проходящем через вершины углов кривых безразличия. Например, можно всегда потреблять комплект 1 чашка кофе + 2 пирожных. Тогда при увеличении количества чашек кофе, нужно пропорционально увеличивать количество пирожных. Если мы купим 1 чашку кофе и 3 пирожных, мы получим тот же уровень полезности, что и когда мы приобретали 1 кофе и 2 пирожных:

Луч решений будет задаваться функцией $y=2x$, если по оси $x$ отложены чашки кофе, а по оси $y$ — пирожные.

Видео:15 Функция полезности определениеСкачать

Функция совокупной полезности потребителя от потребления благ А и В заданы уравнениями TUa=16Qa-Qa2 ; TUb=20Qb-1,5Qb2. Цена блага А (Ра) равна 2, цена блага В (Рb) равна 5.

Готовое решение: Заказ №10064

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Экономика

Дата выполнения: 09.11.2020

Цена: 219 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Функция совокупной полезности потребителя от потребления благ А и В заданы уравнениями TUa=16Qa-Qa2 ; TUb=20Qb-1,5Qb2.

Цена блага А (Ра) равна 2, цена блага В (Рb) равна 5, доход потребителя (I) равен 39.

Найти, какой объем благ А (Qa) и В (Qb) приобретет потребитель, чтобы максимизировать доступную ему совокупную полезность?

Для решения этой задачи необходимо изучить тему «Закономерности потребительского поведения».

Решение:

Максимальный уровень общей полезности обеспечит потребителю рациональный набор в соответствии со вторым законом Госсена:

Определим функцию предельной полезности:

Если вам нужно решить экономическую теорию, тогда нажмите ➔ заказать контрольную работу по экономической теории.

Похожие готовые решения:

Термин «политическая экономия» ввел в научный оборот… а) А.Монкретьен; б) Ф.Кенэ; в) Дж.М.Кейнс; г) П.Самуэльсон.
Заполните таблицу, пояснив способ расчёта каждого показателя: Q, AFC, VC, ATC, MC, TC.
Отрицает необходимость государственного вмешательства в процесс ценообразования: а) кейнсианство; б) неокейнсианство; в) марксизм; г) классическая политэкономия.
В каком из нижеперечисленных случаев достигается минимизация затрат на приобретение ресурсов: Поясните сделанный выбор.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.