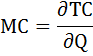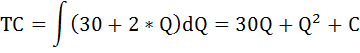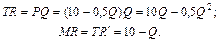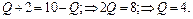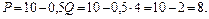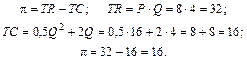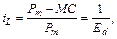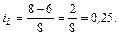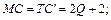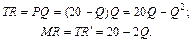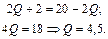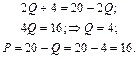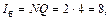- Задача №1. Расчёт экономической прибыли конкурентной фирмы
- Решение:
- Задача № 2. Определение рыночной цены и отраслевого выпуска продукции
- Решение:
- Задача № 3. Определение рыночной цены в долгосрочном периоде
- Решение:
- Задача № 4. Расчёт рыночной цены, при которой фирма уйдёт с рынка
- Решение:
- Решение:
- Задача №6. Расчёт объёма производства в краткосрочном периоде
- Решение:
- Задача № 7. Расчёт рыночной цены и объёма выпуска на конкурентном рынке
- Решение:
- Задача № 8. Расчёт рыночной цены на конкурентном рынке в долгосрочном периоде
- Решение:
- Задача № 9. Расчёт цены и объёма производства, максимизирующих прибыль
- Решение:
- Задача №10. Расчёт рыночной цены и объёма выпуска на конкурентном рынке
- Решение:
- Экономика (стр. 4 )
- Функция предельных издержек каждой из фирм будет описываться уравнением mc
- 2. Железо, дерево и глина
- 3. 1000 спросов
- 4. Евро за килограмм
- 5. Спрос касается AC
- Б. Примеры решения задач
- 💥 Видео
Видео:Решение задачи по экономике на издержки | Как рассчитать предельные издержкиСкачать

Задача №1. Расчёт экономической прибыли конкурентной фирмы
Фирма, находясь в условиях совершенной конкуренции, имеет следующую функцию общих затрат:
ТС = 140 + 10 × Q + 40 × Q 2 .
При каком выпуске прибыль фирмы достигнет максимума, если цена установилась на уровне 250 ден. ед.? Определить размер прибыли фирмы.
Будут ли в длительном периоде в эту отрасль стремиться войти новые фирмы?
Решение:
Наличие в составе общих затрат фиксированных (постоянных) затрат (FC = 140) свидетельствует о том, что речь идёт о краткосрочном периоде.
Найдём объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде имеет вид:
Определим функцию предельных издержек фирмы: найдём производную общих издержек.
МС = (ТС)’ = 10 + 80 × Q.
Приравняем эту функцию к цене равной 250.
Вычислим прибыль фирмы при объёме выпуска равном 3 по формуле:
П = TR — TC = P × Q — TC = 250 × 3 — (140 + 10 × 3 + 40 × 3 2 ) = 220 ден. ед.
В долгосрочном периоде наличие неотрицательной экономической прибыли будет привлекать в отрасль новые фирмы.
Видео:Сложные случаи в выводе предложения фирмы, Рэма Бахарева, преподавателя, Олмат.Экономика олимпиадыСкачать

Задача № 2. Определение рыночной цены и отраслевого выпуска продукции
В отрасли действуют 130 одинаковых фирм. Издержки производства каждой фирмы описываются функциями
ТС =Q 3 — 36*Q 2 + 384*Q,
где
Q — объём производства в тысячах штук. Найти рыночную цену и отраслевой выпуск продукции, при которых на конкурентном рынке устанавливается долгосрочное равновесие.
Решение:
В долгосрочном периоде на рынке совершенной конкуренции соблюдается равенство:
P = MC = MR = AR = minAC.
Найдём функцию средних издержек каждой фирмы по следующей формуле:
АС = ТС / Q = Q 2 — 36*Q + 384
Далее необходимо найти минимум данной функции. Для этого определим производную функции АС и приравняем её к нулю.
AC(18) = 18 2 — 36*18 + 384 = 60
Так как Р = minAC в долгосрочном периоде, следовательно, рыночная цена равна Р = 60.
Найдём отраслевой выпуск. Так как каждая из фирм отрасли производит 18 тысяч штук продукции, значит 130 фирм произведут:
Qотр. = 18*130 = 2340 тысяч штук
Видео:Как спрос и предложение задают ценыСкачать

Задача № 3. Определение рыночной цены в долгосрочном периоде
Конкурентная фирма находится в состоянии равновесия в долгосрочном периоде и имеет следующие затраты: TC = Q 3 — 38*Q 2 + 418*Q. Определите цену на этом рынке в долгосрочном периоде.
Решение:
В долгосрочном периоде цена в условиях соверешенной конкуренции устанавливается на уровне минимума средних затрат. При этом фирма совершенный конкурент получает нулевую экономическую прибыль.
Условие равновесия на рынке будет иметь вид:
Р = МС = МR = AR = min AC
Найдём средние затраты фирмы по формуле:
АС = ТС / Q = Q 2 — 38*Q + 418
Определим минимум функции средних затрат. Для нахождения экстремума функции приравняем к нулю её производную:
При выпуске Q = 19 средние затраты будут равны:
АС = 19 2 — 38*19 + 418 = 57.
Таким образом, цена в долгосрочном периоде будет равна 57.
Видео:Эластичность спроса и предложения | Как цена влияет на спросСкачать

Задача № 4. Расчёт рыночной цены, при которой фирма уйдёт с рынка
Общие затраты фирмы, действующей на рынке совершенной конкуренции, составляют
0,5*Q 3 — 15*Q 2 + 300*Q + 250 000.
При какой цене фирме становится невыгодным работать на этом рынке в краткосрочном периоде?
Решение:
В краткосрочном периоде фирма совершенный конкурент уйдёт с рынка, если цена окажется меньше минимума её средних переменных издержек: Р 3 — 15*Q 2 + 300*Q
Теперь определим функцию средних переменных издержек по формуле:
АVC = VC / Q = 0,5*Q 2 — 15*Q + 300
Найдём экстремум этой функции, приравняв к нулю её производную.
При объёме производства Q = 15 средние переменные издержки будут минимальными.
АVC(15) = 0,5*15 2 — 15*15 + 300 = 187,5
Это так называемая точка закрытия фирмы. Фирма совершенный конкурент уйдёт с рынка, если цена упадёт ниже этой точки в краткосрочном периоде.
При Р 2 — Q + 3, где Q — объём производства. Рыночная цена на продукцию фирмы составляет 7 и не зависит от объёма продаж этой фирмы. Найти объём выпуска продукции, максимизирующий прибыль фирмы.
Решение:
По условию рыночная цена не зависит от объёма продаж этой фирмы, это говорит о том, что фирма функционирует в условиях совершенной конкуренции.
Максимум прибыли фирмы действующей в условиях совершенной конкуренции определяется тождеством: Р = МС.
Найдём предельные издержки фирмы по формуле:
Найдём объём выпуска продукции, максимизирующий прибыль фирмы.
Цена по условию равна Р = 7.
Видео:27. Вычисление предела функции №1. Примеры 1-4Скачать

Задача №6. Расчёт объёма производства в краткосрочном периоде
В отрасли совершенной конкуренции установилась цена Р = 30. В эту отрасль входит фирма с общими издержками ТС = 1/2 * Q 2 + 10 * Q + 100. Найти её объём производства в краткосрочном периоде.
Решение:
Фирма выберет такой объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли: МС = MR.
На рынке совершенной конкуренции предельный доход равен цене: MR = P.
Отсюда следует, что цена равна предельным издержкам: P = MC.
Найдём предельные издержки. Предельные издержки в непрерывном случае (т.е. когда общие издержки заданы функцией) равны производной от функции общих издержек:
Функция предельных издержек будет иметь вид:
МС = Q + 10
P = MC
30 = Q + 10
Q = 20 — оптимальный объём производства фирмы.
Видео:Спрос и предложение разбор задачСкачать

Задача № 7. Расчёт рыночной цены и объёма выпуска на конкурентном рынке
Конкурентная фирма имеет общие затраты
ТС = 800 + 40*Q + 2*Q 2
Она получает в краткосрочном периоде максимально возможную прибыль, равную 1000.
Определить цену на рынке и объём выпуска данной фирмы.
Решение:
Формула прибыли фирмы имеет вид:
П = TR — TC = P*Q — TC
По условию максимально возможная прибыль равна 1000.
P*Q — (800 + 40*Q + 2*Q 2 ) = 1000
Условие максимизации прибыли на рынке совершенной конкуренции имеет вид:
Так как Р = МС, а МС = ТС’ = 40 + 4*Q, следовательно, Р = 40 + 4*Q. Подставим это выражение в формулу прибыли и получим:
(40 + 4*Q)*Q — (800 + 40*Q + 2*Q 2 ) = 1000
40*Q + 4*Q 2 — 800 — 40*Q — 2*Q 2 — 1000 = 0
Так как отрицательный корень экономического содержания не имеет, берём Q = 30.
Тогда цена будет равна:
Р = 40 + 4*30 = 160
Видео:Разбор регионального этапа ВСОШ 2023. Экономика. 10 классСкачать

Задача № 8. Расчёт рыночной цены на конкурентном рынке в долгосрочном периоде
Допустим, общие затраты фирмы на выпуск Q единиц продукции составляют:
Q 3 – 16*Q 2 + 400*Q.
а) При каком значении Q средние затраты достигают минимума?
б) При какой цене этой фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде?
Решение:
а) Найдём функцию средних затрат по формуле:
АС = ТС / Q = (Q 3 – 16*Q 2 + 400*Q) / Q = Q 2 – 16*Q + 400
Определим минимум функции. Для нахождения экстремума функции необходимо найти её производную и приравнять её к нулю.
AC’ =(Q2 – 16*Q + 400)’ = 2*Q – 16
2*Q – 16 = 0
Q = 8
При Q = 8 средние затраты достигают минимума.
б) В долгосрочном периоде фирме становится выгодным участвовать в совершенной конкуренции, если Р ≥ АС. При этом фирма имеет нулевую прибыль. И выполняется условие:
Р = МС = MR = minАС
Рассчитаем minAC. Подставим Q = 8 в функцию средних затрат:
minAC(Q=8) = 82 – 16*8 + 400 = 336
Итак, при цене Р ≥ 336 фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде.
Видео:Олимпиадная экономика. Вся теория для региона за 5 часовСкачать

Задача № 9. Расчёт цены и объёма производства, максимизирующих прибыль
Спрос на продукцию конкурентной отрасли:
Qd = 55 – P
Предложение:
Qs = 2P – 5
Если у одной из фирм отрасли восходящий участок кривой предельных издержек:
При каких цене и объёме производства фирма максимизирует прибыль?
Решение:
Найдём цену равновесия. Приравняем функцию спроса и предложения:
Qd = Qs
55 – P = 2P – 5
3 * Р = 60
Р = 20 – цена рыночного равновесия, то есть цена по которой фирмы будут продавать свою продукцию.
Фирма в условиях совершенной конкуренции получает максимум прибыли при условии равенства цены и предельных затрат.
МС = Р
3Q + 5 = 20
Q = 5 – объём производства, при котором прибыль фирмы будет максимальной.
Видео:15 Функция полезности определениеСкачать

Задача №10. Расчёт рыночной цены и объёма выпуска на конкурентном рынке
Конкурентная фирма имеет предельные затраты:
МС = 30 + 2 × Q
при фиксированных затратах, равных 500 денежным единицам.
Она получает в краткосрочном периоде максимально возможную прибыль, равную 1100 денежным единицам.
Определить цену на рынке и объём выпуска данной фирмы.
Решение:
Формула прибыли имеет вид:
П = TR – TC = P*Q – TC
Определим функцию общих затрат. Так как функция предельных затрат это производная функции общих затрат, следовательно, функцию общих затрат можно определить как первообразную от функции предельных затрат.
С – константа, равная величине фиксированных затрат, которые по условию равны 500.
Таким образом функция общих затрат имеет вид:
ТС = Q 2 +30*Q + 500
Теперь запишем условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде:
Р = МС = MR = AR
Воспользуемся тем, что:
По условию задачи:
МС = 30 + 2 × Q, то есть Р = 30 + 2 * Q
Подставим это выражение, а так же функцию общих затрат в формулу прибыли и получим уравнение с одной неизвестной.
(30 + 2 * Q) * Q – (Q 2 +30*Q + 500) = 1100
Q2 = 1600
Q = ± 40
Так как отрицательное значение Q экономического смысла не имеет, следовательно, объём выпуска данной фирмы Q = 40.
Видео:ЭКОНОМИКА ОЛИМПИАДЫ. Вся необходимая теория для муниципального этапаСкачать

Экономика (стр. 4 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |
5.5 Примеры заданий-кейсов
В конкурентной отрасли действует 200 одинаковых фирм, каждая из которых имеет следующую функцию общих издержек: TC = 4q2 +2q + 0,5, где TC – величина общих издержек одной фирмы (ден. ед.), q – объем производства каждой фирмы (ед.).
Спрос на продукцию данной отрасли сократился из-за снижения доходов потребителей и теперь описывается уравнением QD= 70 – 5P , где QD– объем спроса (ед.), P – цена за единицу (ден. ед.).
Функция предельных издержек каждой из фирм будет описываться уравнением MC = …..
2) 800q2 + 400q +50
Исследование рынка показало, что продукция фирм данной отрасли однородна, объем производства на всех фирмах одинаков и цена равна предельным издержкам. Следовательно, функция предложения данной отрасли описывается уравнением QS = ______________, а сама отрасль является рынком ____________ конкуренции.
Совокупный объем производства отрасли при условии, что рынок после сокращения спроса находится в равновесии, составит _______ единиц.
Спрос и предложение на рынке некоторого продукта описываются уравнениями QD = 25 – 0,2P и QS = 4P – 80, где QD – объем спроса (тыс. шт.), QS – объем предложения (тыс. шт.), P – цена, ден. ед.
Государство вмешалось и установило минимальную цену на товар в размере 30 ден. единиц за 1 тыс. шт. Примером рынка с таким участием государства может служить рынок …
1)пшеницы в сверхурожайный год
3)товаров первой необходимости
4)крепких спиртных напитков
Установление минимальной цены имеет целью помочь _____________ и приведет к ситуации ______________ товара на рынке.
До вмешательства государства рынок характеризовался как равновесный с объемом продаж ____________ тыс. шт.
На начало текущего месяца Комитет государственной статистики страны Сигма опубликовал актуальные данные о ее населении. Общая численность населения составила 77 млн чел., из которых 25 млн чел. являлись нетрудоспособными. К занятым были отнесены 32 млн чел., к безработным – 8 млн чел., из которых 3 млн чел. потеряли работу из-за переездов или собственного желания улучшить условия труда, 2 млн чел. не могли устроиться, так как их профессия оказалась невостребованной, а остальные были сокращены в результате общего падения объемов производства в стране.
Подзадача 1
Естественный уровень безработицы относительно стабилен в краткосрочном периоде и включает в себя _______________ виды безработицы (2 ответа).
В соответствии с данными, опубликованными Комитетом государственной статистики Сигмы, верными являются утверждения о том, что …
1)численность рабочей силы в стране составляет 40 млн чел.
2)уровень безработицы составляет 20 %
3)общая численность безработных – 33 млн чел.
4)структурной безработицей охвачено 2 млн чел.
Установите соответствие между видами безработицы и способами их сокращения.
1) Фрикционная безработица
2) Структурная безработица
3) Циклическая безработица
а) создание общедоступных баз данных с вакансиями в сети Интернет
б) реализация программ профессиональной переподготовки кадров
в)создание новых рабочих мест
г)стимулирование занятости среди пенсионеров
Обучающийся показывает полную сформированность навыков решения практических экономических задач, использования экономических методов для решения жизненных и профессиональных проблем
Обучающийся показывает сформированность навыков решения практических экономических задачи использования экономических методов для решения жизненных и профессиональных проблем, достаточную для осуществления профессиональной деятельности
Обучающийся показывает неполную сформированность навыков решения практических экономических задач, использования экономических методов для решения жизненных и профессиональных проблем, недостаточную для осуществления успешной профессиональной деятельности
Обучающийся показывает несформированность навыков решения практических экономических задач, использования экономических методов для решения жизненных и профессиональных проблем
Обучающийся показывает полную несформированность навыков решения практических экономических задач, использования экономических методов для решения жизненных и профессиональных проблем, что делает невозможным осуществление успешной профессиональной деятельности
5.6 Контрольные вопросы для самостоятельной оценки качества освоения дисциплины и собеседования с преподавателем
- Основные экономические школы.
- Методы экономических исследований.
- Экономические агенты и их интересы.
- Сущность и формы собственности.
- Сущность и методы приватизации.
- Кругооборот доходов, ресурсов и продуктов.
- Формы и виды предпринимательства.
- Классификация благ, потребностей и ресурсов.
- Характеристики кривой производственных возможностей.
- Рынок, его структура и виды рынка.
- Функции, объекты и субъекты рынка.
- «Фиаско» рынка и государства.
- Виды конкуренции и методы конкурентной борьбы.
- Понятие эффективности и Парето-эффективности.
- Показатели эффективности и результативности функционирования хозяйственной системы.
- Сущность закона спроса и предложения.
- Факторы, влияющие на спрос и предложение.
- Механизм установления параметров рыночного равновесия.
- Понятие излишка потребителя и производителя.
- Формулы эластичности спроса по цене, по доходу, перекрестной эластичности, эластичности предложения.
- Теория предельной полезности.
- Концепция кривых безразличия и бюджетного ограничения.
- Определение оптимума потребителя.
- Производственная функция и ее свойства.
- Отдача от масштаба.
- Издержки производства в краткосрочном и долгосрочном периодах.
- Расчет различных видов издержек.
- Основные характеристики рынка совершенной конкуренции.
- Условие максимизации прибыли при совершенной конкуренции.
- Понятие и виды монополии.
- Принципы монополистического ценообразования и ценовая дискриминация.
- Монопольная прибыль, монопольная цена и монопольный объем производства.
- Особенности монополистической конкуренции.
- Характерные черты рынка олигополии.
- Принципы спроса на факторы производства и их предложение.
- Сущность рынка капитала и условия инвестирования в капитал.
- Спрос и предложение на рынке труда.
- Спрос на землю и предложение земли.
- Земельная рента и цена земли.
- Виды внешних эффектов.
- Общественные блага: спрос и предложение, поиск ренты.
- Методы макроэкономического анализа.
- Модели кругооборота доходов и продуктов в национальной экономике.
- Основные макроэкономические показатели.
- Дефлятор ВВП, индекс потребительских цен.
- Предельная склонность к потреблению и сбережению.
- Сущность инвестиций и факторы, влияющие на инвестиции.
- Сущность мультипликатора и его роль в макроэкономике.
- Сущность совокупного спроса и совокупного предложения, факторы, влияющие на них.
- Сущность равновесия между совокупным спросом и предложением, модель AD-AS.
- Причины, формы и социально-экономические последствия безработицы.
- Сущность, причины, виды и социально-экономические последствия инфляции.
- Влияние инфляции на процентную ставку.
- Кривая Филлипса для оценки выбора между инфляцией и безработицей.
- Понятие, структура и типы экономических циклов.
- Технологические уклады и «длинные волны».
- Причины циклического развития экономики.
- Сущность, факторы и типы экономического роста, золотое правило накопления.
- Анализ воздействие шоков на макроэкономическое равновесие.
- Сущность и функции денег.
- Структура банковской системы страны.
- Функции центрального и коммерческих банков страны.
- Денежные агрегаты.
- Сущность денежного мультипликатора.
- Сущность и виды налогов.
- Сущность и инструменты бюджетно-налоговой политики.
- Доходы и расходы государственного бюджета.
- Сущность и инструменты денежно-кредитной политики.
- Классификация и характеристика основных видов ценных бумаг.
- Механизм функционирования рынка ценных бумаг.
- Формы международных экономических отношений.
- Принцип сравнительного преимущества.
- Свободная торговля и методы протекционизма.
- Фиксированный и плавающий валютный курсы.
- Паритет покупательной способности, платежный баланс.
Обучающийся показывает полное усвоение теоретических знаний по дисциплине, сформированную способность использовать полученные знания в жизни и профессиональной деятельности
Обучающийся показывает усвоение теоретических знаний по дисциплине, сформированную способность использовать полученные знания в жизни и профессиональной деятельности, достаточное для осуществления профессиональной деятельности
Обучающийся показывает неполное усвоение теоретических знаний по дисциплине, неполностью сформированную способность использовать полученные знания в жизни и профессиональной деятельности
Обучающийся показывает слабые теоретические знания по дисциплине, слабую сформированную способность использовать полученные знания в жизни и профессиональной деятельности, недостаточные для осуществления профессиональной деятельности
Обучающийся показывает отсутствие теоретических знаний по дисциплине, отсутствие способности использовать полученные знания в жизни и профессиональной деятельности
Видео:Математический анализ, 5 урок, Непрерывность функцииСкачать

Функция предельных издержек каждой из фирм будет описываться уравнением mc
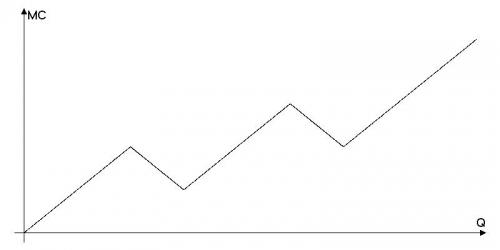
В связи с внедрением сложной системы субсидирования график предельных издержек совершенно конкурентной фирмы имеет несколько нетипичный вид:
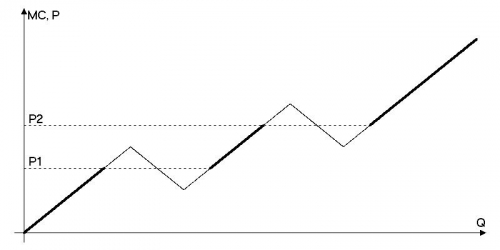
Постройте на этом же графике кривую предложения фирмы и подробно объясните свое решение.
Если уравнение $MC(Q) = P$ имеет один корень, кривая предложения совпадает с кривой $MC$.
Если корней несколько, то нужно выбрать тот выпуск, при котором прибыль будет больше. Во-первых, заметим, что мы никогда не выберем точку на убывающем участке $MC$, так как это точка локального минимума функции прибыли. Значит, мы всегда будем выбирать только корень уравнения $MC(Q) = P$, лежащий на возрастающем участке графика $MC$.
На следующем этапе для определения оптимального выпуска необходимо сравнить величины прибыли, которую фирма получит, выбирая больший или меньший объемы выпуска, соответствующие возрастающим участкам графика $MC$. Для этого удобно использовать площади треугольников, заключенных между графиками $P$ (для какого-то $P$) и $MC$. Площадь «верхнего» треугольника при каком-то $P$ равна дополнительным убыткам перехода от меньшего выпуска к большему, а «нижнего» — дополнительным выгодам. Тогда если больше площадь «нижнего» — то есть дополнительные выгоды больше дополнительных убытков – то кривой предложения будет принадлежать больший выпуск. Если же больше площадь «верхнего» треугольника – то есть дополнительные убытки больше дополнительных выгод – то выгоднее будет производить меньший объем выпуска.
Если площади указанных треугольников равны (как при ценах$P_1$ и $P_2$) – возникает точка разрыва функции предложения; фирме безразлично, какой из двух объемов выбрать (при этом обе интересующие нас точки включаются в график кривой предложения).
Поскольку указанные треугольники подобны, $P_1$ лежит ровно посередине между соответствующими локальным максимумом и минимумом $MC$. Аналогично для $P_2$.
2. Железо, дерево и глина
В античном городе N в производстве различных товаров используются три вида ресурсов: Железо (A), Дерево (B) и Глина (C). Кривая, описывающая возможности города в добыче ресурсов, задается уравнением $A^2+B^2+C^2=90000$. Все производимые в городе товары можно разделить на две группы: Военные Товары (X) и Мирные Товары (Y). В среднем для производства единицы Мирных Товаров необходимы 1 единица Железа, 2 единицы Дерева и 2 единицы Глины. Для производства единицы Военных Товаров нужно 4 единицы Железа и 3 единицы Дерева, Глины не нужно вовсе.
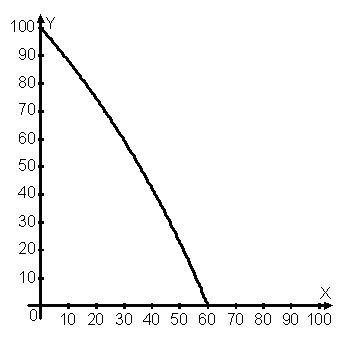
Война с античным городом М не за горами, поэтому необходимо точно оценить потенциал города в производстве Военной и Мирной продукции. Выведите уравнение кривой производственных возможностей города N в координатах (X,Y) и постройте её график, указав максимально возможные объемы производства военных и мирных товаров.
Для производства Х единиц Военной и Y единиц Мирной продукции нужно $A = 4X + Y$единиц Железа, $B = 3X + 2Y$ единиц Дерева, $C = 2Y$ единиц Глины. Подставляя эти выражения в КПВ ресурсов, получаем:
$(4X + Y)^2 + (3X + 2Y)^2 + (2Y)^2 = 90000 $ или $25X^2 + 20XY + 9Y^2 = 90000$.
Это и есть искомое уравнение КПВ. Решив это уравнение относительно Y, можно получить явную зависимость Y(X): $Y = <<sqrt — 10X> over 9>$ (хотя делать это, в принципе, не обязательно).
КПВ будет иметь обычный вогнутый вид, max(X) = 60, max(Y) = 100.
Ответ: Уравнение кривой, описывающей возможности города в производстве военной и мирной продукции:$Y = <<sqrt — 10X> over 9>$. Максимально возможный объем производства военных товаров равен 60, мирных товаров – 100.
3. 1000 спросов
На рынке присутствуют 1000 покупателей, для удобства дальнейших рассуждений пронумерованных индексами $i=1, 2, 3, dots, 1000$. Функция спроса i-го покупателя имеет вид: $q_i=1001-i-P$. Причем цены могут принимать только целые значения. Производит и продает товар фирма-монополист, функция общих издержек которой имеет вид $TC=100,5Q$. Сколько единиц товара и по какой цене продаст монополист, не имеющий возможности осуществлять ценовую дискриминацию? Какую прибыль он получит?
Очевидно, график функции спроса каждого отдельного покупателя будет представлять тобой отрезок прямой. Поскольку индивидуальные графики спроса начинаются при различных максимальных значениях цены, то суммарная (рыночная) функция спроса будет иметь график, представляющий собой ломаную линию. Представим точки перелома этой линии в виде таблицы, формулирующей зависимость между ценой и объемом товара, приобретенного всеми покупателями:
| P | 1000 | 999 | 998 | 997 | … | P |
| Q | 0 | 1 | 1+2 | 1+2+3 | 1+2+3+…+1000-P |
Используя формулу суммы членов арифметической прогрессии, можно записать:
$Q(P)=1+2+3+dots+(1000-P)=\= <over 2> cdot (1000 — P)=0,5(1001-P)(1000-P) $
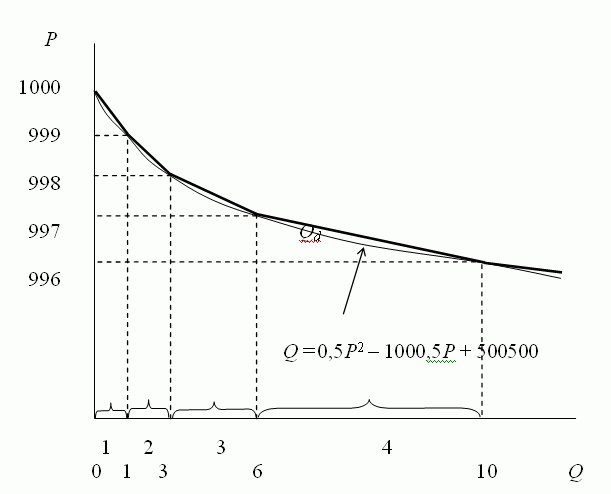
Разумеется, это уже не график ломаной линии. Это парабола, которая при целых значениях Р и Q проходит через точки ломаной линии спроса. Однако, именно при целых значениях данная зависимость нас и интересует. Графически полученный результат можно представить следующим образом:
Запишем выражение для прибыли монополиста при определенном значении Р:
$pi =TR-TC=Pcdot Q(P)-100,5cdot Q(P)=\=(P-100,5) cdot 0,5(P-1001)(P-1000)$
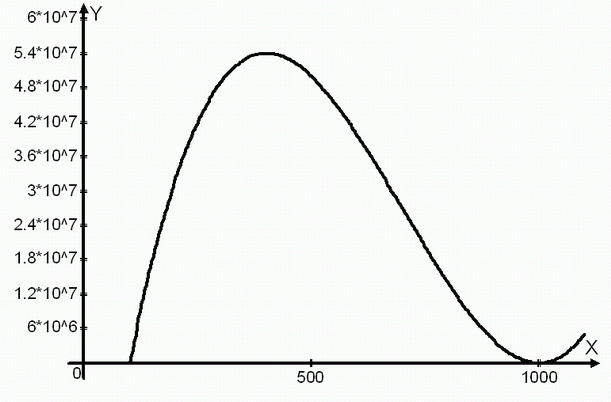
График этой функции – кубическая парабола, проходящая через точки 100,5; 1000; 1001.
Спрос определен при $Q le 1000 $. На участке (100,5;1000) эта функция имеет максимум. Найдем P такое, что $pi(P)=pi(P-1) $. Если это P целое, то P и P-1 – точки с максимальной прибылью среди всех целых P. Если это P не целое, то максимальную прибыль обеспечит целое число, лежащее между (P-1) и P.
pi(P)=pi(P-1) \ (P-100,5)*0,5(P-1001)(P-1000)=(P-101,5)*0,5(P-1002)(P-1001)\(P-100,5)(P-1000)=(P-101,5)(P-1002)\P^2 — 1100,5P + 100500 = P^2 — 1103,5P + 101703\3P = 1203\P = 401
Значит, P=401 и P=400 являются решениями задачи.
4. Евро за килограмм
- 0 t>12; 22-0,2Q=1+0,1Q+t; Q=70-3,33t
- 30 t>17/6; 22-0,2Q=2,5+0,05Q+t; Q=78-4t
- 66,67 t>0; 12-0,05Q=2,5+0,05Q+t; Q=95-10t
5. Спрос касается AC
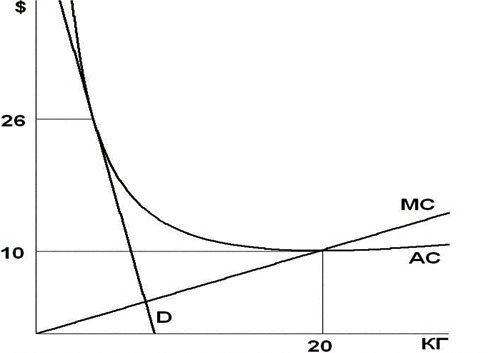
На рисунке представлены графики предельных (MC) и средних (АС) издержек фирмы-монополиста. А также график спроса на его продукцию (D).
Определите, какой объем выпуска должна выбрать фирма, чтобы максимизировать прибыль (минимизировать убытки)? Восстановите уравнение кривой спроса.
Функция предельных издержек проходит через точки $(0;0)$ и $(20;10)$, следовательно, предельные издержки заданы уравнением: $MC(Q)=0,5Q$. Значит, уравнение общих издержек имеет вид: $TC(Q)=0,25Q^2+FC$. Отсюда $FC=100$. Функция средних издержек задается уравнением: $AC(Q) = frac = 0,25Q + frac
$.
Из графика видно, что при объеме, соответствующем $P=26$, средние издержки равны 26 долларам и следовательно прибыль монополиста равна нулю. При любом другом объеме график спроса лежит ниже графика средних издержек, следовательно, прибыль монополиста отрицательна. Поэтому максимальная (нулевая) прибыль монополиста достигается при цене, равной 26. Значит, оптимальный объем выпуска, как следует из графика, является наименьшим из корней уравнения: $AC(Q) =26$. $0.25Q + frac = 26 Leftrightarrow Q^2 — 104Q + 400 = 0 Leftrightarrow Q=4 Q=100.$ Нас устраивает наименьший из корней: $fbox
$.
Нам известна одна точка на кривой спроса: $Q=4 ; P=26.$ Так что $MC(4) = 2; MR(4) = 2 ; Q_d(2) = 8$ (кривая спроса вдвое положе кривой $MR(Q)$). Таким образом, нам известна вторая точка на кривой спроса: $ Q=8 ; P=2$ и уравнение кривой спроса: $fbox
$
Видео:Экономика. Олимпиады. Теория игр. Модели олигополии. Приоткрытый вебинар.Скачать

Б. Примеры решения задач
Задача 4.1.Функция спроса на продукцию фирмы-монополиста: P = 10 – 0,5Q, функция общих издержек фирмы описывается уравнением: TC = 0,5Q 2 + 2Q.
Определите цену и объём выпуска, при которой прибыль фирмы-монополиста будет максимальна. Какую прибыль при этом получит фирма? Рассчитайте степень монопольной власти фирмы.
Решение. Чистая монополия максимизирует свою прибыль при условии:
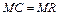
Определим МС, используя формулу (3.5):

Определим MR, используя формулы (3.6) и (3.8):
Оптимальный объём производства и реализации продукции для фирмы-монополиста будет Q = 4.
Для определения цены продукции фирмы подставим объём в уравнение спроса:
Прибыль монополии составит:
Степень монопольной власти монополиста отражает индекс Лернера:
где iL – индекс монопольной власти Лернера;
МС – предельные издержки;
Ed – эластичность спроса по цене.
Индекс Лернера, для данной фирмы-монополиста:
То есть фирма-монополист может превысить цену, характерную для свободной конкуренции, на 25 %.
Задача 4.2.Функция общих затрат фирмы монополиста: TC = Q 2 + 2Q Функция спроса на её продукцию: P = 20 – Q.
Государство вводит потоварный налог (на каждую единицу продукции) в количестве 2 ден. ед. Определите налоговые поступления в бюджет, объём выпуска и цену, максимизирующие прибыль монополиста, до и после введения налога.
Решение. До введения налога монополия максимизирует свою прибыль при условии MR = MC. Следовательно:
При объёме производства и реализации продукции Q = 4,5 монополия будет максимизировать свою прибыль. Определим монопольную цену реализации продукции:
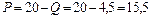
Введение налога сокращает предложение монополии. Кривая МС – это кривая предложения монополии, следовательно:
Объём производства и цена реализации продукции составят:
Поскольку монополист уплачивает налог в размере 2 ден. ед. за каждую единицу продукции, тогда налоговые поступления в бюджет (Iб):
где N – налоговая ставка на единицу продукции.
Задача 4.3.В таблице 4.1 представлены данные фирмы-монополиста. Рассчитайте МС, ATC, TR, MR, Pr.
Т а б л и ц а 4.1 – Данные фирмы-монополиста
| Q | P | TC | ATC | МС | TR | MR | π |
| – | – | – |
Выполните следующие задания:
а) постройте кривые МС, МR, ATC и D (спроса);
б) определите, при каком объёме фирма будет максимизировать свою прибыль, какую цену монополист назначит на свою продукцию.
Решение. Рассчитаем МR, MC, TR, ATC, Pr, используя формулы (3.1) – (3.8), полученные данные сведём в таблицу 4.2:
Т а б л и ц а 4.2 – Издержки, доход и прибыль фирмы-монополиста
| Q | P | TC | ATC | МС | TR | MR | π |
| – | – | – | –5 | ||||
| 8,0 | |||||||
| 7,0 | |||||||
| 7,7 | |||||||
| 9,3 | |||||||
| 11,0 | –5 | ||||||
| 12,8 | –2 | –29 |
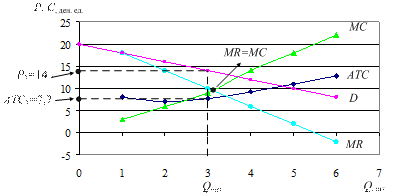
1 На основании таблицы построим графики МС, МR, D, ATC (рисунок 4.1).
Рисунок 4.1 – Кривые издержек и дохода монополиста
2 Фирма максимизирует свою прибыль при условии MC = MR. Это равенство выполняется при Qопт = 3. При производстве трёх единиц товара и реализации их по цене Р1 = 14 ден. ед., фирма-монополист получит максимальную прибыль π = 19 ден. ед.
В. Тесты
1 Монополист стремится:
а) продавать продукцию одному потребителю по единой цене;
б) увеличивать объём производства по сравнению с конкурентной фирмой, чтобы минимизировать издержки на единицу продукции;
в) максимизировать прибыль, снижая цену на продукт и сокращая предельный доход;
г) максимизировать прибыль, при объёме выпуска, отвечающего условию равенства предельного дохода и предельных издержек.
2 В модели чистой монополии предполагается, что:
а) на рынке товары приобретает один покупатель;
б) на рынке действует множество продавцов товаров;
в) вход других фирм на рынок связан с некоторыми ограничениями;
г) продукт фирмы уникален и не имеет заменителей.
3 Вид монополии, которая защищена от конкуренции с помощью юридических ограничений, называется:
а) открытой монополией;
б) закрытой монополией;
в) естественной монополией;
4 Кривая спроса монополиста:
а) совпадает с кривой предельных издержек;
б) параллельна горизонтальной оси объёма выпуска;
в) совпадает с кривой спроса всей отрасли;
г) перпендикулярна кривой спроса при совершенной конкуренции.
5 Кривая предельного дохода монополиста, не занимающегося ценовой дискриминацией:
а) расположена выше кривой спроса;
б) совпадает с кривой спроса;
в) расположена ниже кривой спроса;
г) пересекает кривую предельных издержек монополиста в точке минимального значения.
6 Монополист может получать экономическую прибыль:
а) в краткосрочном периоде;
б) долгосрочном периоде;
в) краткосрочном и долгосрочном периоде;
г) нет верного ответа.
7 «X-неэффективность» монополии проявляется:
а) в завышении цены на произведённый продукт;
б) неспособности произвести объем продукции при минимальных средних издержках;
в) сокращении объёма производства по сравнению с уровнем при совершенной конкуренции;
г) сокращении налоговых поступлений в бюджет государства.
8 К негативным последствиям чистой монополии можно отнести:
а) превышение объёма выпуска по сравнению с конкурентной отраслью;
б) неэффективное использование привлечённых ресурсов;
в) неспособность получать нормальную прибыль в долгосрочном периоде;
г) избыточный объём инвестиций во внедрение достижений научно-технического прогресса.
9 Ценовая дискриминация – это:
а) возможность установления различного уровня цен на один и тот же продукт;
б) стремление монополиста к установлению максимально возможных цен на свою продукцию;
в) возможность монополиста самостоятельно устанавливать цену на рынке (в отличие от чистоконкурентной фирмы);
г) превышение ставки налога на монопольную продукцию по сравнению с конкурентными отраслями.
10 Использование ценовой дискриминации позволяет монополисту:
а) сократить издержки производства;
б) увеличить монопольную прибыль;
в) сократить объём выпуска по сравнению с недискриминирующим монополистом;
г) увеличить спрос на производимую продукцию;
д) перераспределить свой излишек в пользу потребителя.
11 Монопсония – это:
а) отрасль с единственным продавцом товара, не имеющего близких заменителей;
б) ситуация, когда в отрасли единственный покупатель продукции;
в) то же самое, что и двусторонняя монополия;
г) положение на рынке, когда власть монополии ограничена государством.
12 Дилемма регулирования естественной монополии государством состоит в выборе:
а) объёма оптимального выпуска естественной монополии, с целью максимального удовлетворения потребностей общества;
б) между социально-оптимальной ценой (P = MC) и ценой, обеспечивающей безубыточность функционирования фирмы (P = ATC);
в) разрешать или нет ценовую дискриминацию монополисту;
г) регулировать или нет деятельность монополии.
Г. Задачи
Задача 4.4. В таблице 4.3 представлены данные об издержках фирмы-монополиста. Функция рыночного спроса представлена уравнением 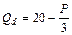
Т а б л и ц а 4.3 – Данные об издержках фирмы-монополиста
| Q |
| TC |
Выполните следующие задания:
1) постройте кривые МС, МR, ATC и D;
2) определите, при каком объёме фирма будет максимизировать свою прибыль, какую цену монополист назначит на свою продукцию;
3) рассчитайте объём максимальной прибыли монополиста.
Задача 4.5. Функция спроса на продукцию фирмы-монополиста представлена уравнением 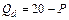
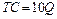
1) какой объём производства и уровень цены выберет монополист, чтобы максимизировать свою прибыль;
2) объём полученной прибыли;
3) чистые потери общества от существования монополии на данном рынке.
Сделайте вывод об эффективности функционирования отрасли.
Задача 4.6. Фирма, действующая на рынке товара A, максимизирует прибыль, продавая его по цене 10 ден. ед. за штуку. По оценкам отдела маркетинга компании, рыночный спрос на товар таков, что при снижении цены до 8 ден. ед., объём продаж увеличится в 2 раза. Оцените рыночную власть фирмы.
Задача 4.7. Фирма-монополист проводит политику ценовой дискриминации, продавая продукцию трём группам потребителей по разным ценам. Функции спроса потребителей на продукцию монополии:
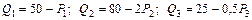
где Q1,2,3 и P1,2,3 – объём спроса и цена для каждой группы потребителей.
Функция общих издержек фирмы описывается уравнением TC = 10Q.
1) определите, какую цену назначит на свою продукцию монополист, максимизирующий прибыль, на каждом сегменте рынка;
2) рассчитайте объём выпуска и прибыль от реализации продукции на каждом сегменте рынка и общие значения по рынку;
3) предположим, что монополист не занимается ценовой дискриминацией и реализует произведенную продукцию по единой цене различным группам потребителей. Рассчитайте объём выпуска, уровень цен и прибыль монополиста.
Выгодна ли монополисту стратегия ценовой дискриминации?
💥 Видео
Предельная полезностьСкачать

Разбор регионального этапа ВсОШ9 классСкачать

Функция потребленияСкачать

Монополистическая конкуренция и экономическая прибыльСкачать

Главные части функций. Частичные пределы. Интегрирование.Скачать

Разбор задач пробной олимпиады по экономике №1Скачать

Урок 28. Экономика. Решение экономических задач.Скачать

Сколько регионов ВсОШ по экономике можно решить за 120 минут?Скачать