Про уравнения - легко » Статьи

Функция лагранжа и уравнения лагранжа системы материальных точек

Обновлено
Содержание
  1. Функция Лагранжа системы материальных точек
  2. Функция Лагранжа системы материальных точек
  3. Примеры решения, формулы и задачи
  4. Принцип наименьшего действия. Уравнения Лагранжа
  5. Теоретическая механика. Уравнения Лагранжа
  6. 🔥 Видео

Видео:Форш П. А. - Теоретическая механика - Формализм Лагранжа. Уравнения Лагранжа для материальной точкиСкачать

Форш П. А. - Теоретическая механика - Формализм Лагранжа. Уравнения Лагранжа для материальной точки

Функция Лагранжа системы материальных точек

Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек

Функция лагранжа и уравнения лагранжа системы материальных точек

Видео:Уравнения Лагранжа второго рода. Задача 1Скачать

Уравнения Лагранжа второго рода. Задача 1

Функция Лагранжа системы материальных точек

  • Здесь важным моментом для рассмотрения системы взаимодействия Только друг с другом, т.е. с незнакомыми людьми Тело, которое не взаимодействует, такая система называется замкнутой.

Можно видеть, что взаимодействие между точками материи можно описать, добавив конкретную координатную функцию x) (в зависимости от характера взаимодействия) к невзаимодействующей точке (4.2) к функции Лагранжа.

Называется кинетическая энергия Людмила Фирмаль

Выражая эту функцию с помощью -C / = t5? -ir (ri, r2, …) (5.1) (Ha — радиус-вектор i-й точки). Это общий вид функции. Лагранжева замкнутая система. Сумма 2 J1 _ y ^ но , функция U называется потенциальной Энергия всего тела, значение этих имен разъясняется в §6. Тот факт, что потенциальная энергия зависит только от расы Положение всех материальных точек одновременно означает, что изменение их положения немедленно влияет на все остальные точки.

Можно сказать, что взаимодействие «распространяется» мгновенно. Неизбежность этого свойства взаимодействия в классической механике тесно связана с последней основной предпосылкой — абсолютностью времени и принципом относительности Галилея.

Видео:Функция Лагранжа. Уравнения Лагранжа. Интегралы движения.Скачать

Функция Лагранжа. Уравнения Лагранжа. Интегралы движения.

Примеры решения, формулы и задачи

Решение задачЛекции
Расчёт найти определенияУчебник методические указания
  • Если взаимодействие не распространялось сразу, то есть абсолютность времени автоматически означает применимость нормального правила добавления скорости ко всем явлениям, эта скорость отличается при конечной скорости ( Зависит от системы отсчета (движутся друг с другом).

Но в этом случае законы движения взаимодействующих объектов различны в разных (инерциальных) системах отсчёта, которые противоречат друг другу Это становится принципом относительности. В §3 мы только упомянули равномерность времени. Для отображения Функция Лагранжа (5.1) показывает, что время не только равномерно, но и изотропно.

поэтому уравнение движения не изменится Людмила Фирмаль

Его характеристики одинаковы в обоих направлениях. Фактически, если вы замените t на -t, функция Лагранжа останется, . Другими словами, если в системе возможно любое движение, обратное движение всегда возможно. Система, которая проходит через то же состояние в обратном порядке.

В этом смысле все движения, которые происходят по законам классической механики, являются обратимыми. Если вы знаете функцию Лагранжа, вы можете создавать уравнения Движение d5L = 5L, dtdwa dva ‘^ ’ Подставляя здесь (5.1), два ди / со о T’IG = ST (5’3) Эта форма уравнения движения называется уравнением Ньютона и представляет собой основу динамики системы взаимодействующих частиц. вектор F „= -g, (5.4) Стоя на правой стороне уравнения (5.3) называется силой в i-й точке.

Наряду с U, это зависит от координат всех частиц, но не от скорости. Следовательно, уравнение (5.3) показывает, что вектор ускорения частицы является функцией только координат. Потенциальная энергия Точность, с которой можно добавлять произвольные константы.

Там Некоторые дополнения не изменяют уравнение движения (частный случай неоднозначности функции Лагранжа показан в конце § 2). Наиболее естественным и общепринятым способом выбора этой константы является то, что потенциальная энергия стремится к нулю при увеличении расстояния между частицами.

В случае неортогональная Ордината точки и любые обобщенные координаты Чтобы получить функцию Лагранжа, нужно выполнить соответствующее преобразование Xa = / a (9 1, 9 2, Qs), = I.T. к Присвойте эти выражения функциям B = 5yPa (Xa + b1 +%)

U, но Получить желаемую функцию Лагранжа. L = ^ 2 aik (q) mk -u (q), (5.5) Где dik — только координатная функция.

Кинетическая энергия Обобщенные координаты все еще вторичны Это функция скорости, но также зависит от координат. Пока что мы обсуждали только закрытые системы. Теперь рассмотрим открытую систему A, которая взаимодействует с другой системой 5, которая выполняет определенное движение.

В этом случае говорят, что система A перемещается в заданное внешнее поле (созданное системой B). Уравнение движения может быть найдено из принципа минимального действия, изменяя каждую координату независимо (то есть, предполагая, что другие координаты известны), так что функция может быть найдена.

LaGrange La System A использует функции Лагранжа. Система А + В в целом Л. Замените координату qs заданной временной функцией. Предполагая, что система A + B закрыта, L = Ta (taAa) + Tv (yavLv) -U (qA, qB), Где первые два члена — это кинетические энергии систем A и 5, а третий член — их совокупная потенциальная энергия.

Замените данную функцию времени вместо qs и опустите время T (qy (Ј), ## (Ј)). La = Ta (caLa) -U (qA, qB (t)). Следовательно, движение системы во внешнем поле Лагранжева функция нормального типа с единственной разницей Потенциальная энергия теперь может явно зависеть от времени.

Поэтому для движения одной частицы во внешнем поле Вид функции Лагранжа 2 L = ^ -U (r, t), (5.6) И уравнение движения — = Vm9U / k—. (5.7) Поле называется однородным и во всех отношениях Та же сила Ф. действует на потенциал. Такие поля явно равны U = -F r. (5.8) В конце этого раздела мы сделаем следующие замечания о применении уравнения Лагранжа к различным конкретным задачам.

Во многих случаях, как говорит взаимодействие тел (материальных точек), характер связи, то есть ограничения, накладываемые на относительное положение тела. На самом деле такое объединение выполняется соединением О кузове с различными стержнями, нитками, петлями и т. Д.

Стоя представляет новый фактор движения тела-движения С трением в месте их контакта, результат состоит в том, что, вообще говоря, задача выходит за рамки чисто механики (см. § 25). Тем не менее, часто трение в системе Влияние на движение настолько слабо, что оно полностью игнорируется.

Кроме того, если массой «неподвижного элемента» системы можно пренебречь, последняя роль просто сводится к уменьшению числа степеней свободы системы s (по сравнению с числом 3N). Функция Лагранжа формы (5.5) может быть снова использована для определения ее движения.

Количество независимых обобщенных координат, соответствующее фактическому количеству степеней свободы. Задание Найти функцию Лагранжа следующей системы в однородном гравитационном поле (ускорение g-гравитации). 1. Двойной плоский маятник (рис. 1). Решения. Взять в качестве координаты Угол (pi и (p2, нити 1 и I2 образуют вертикальную линию.

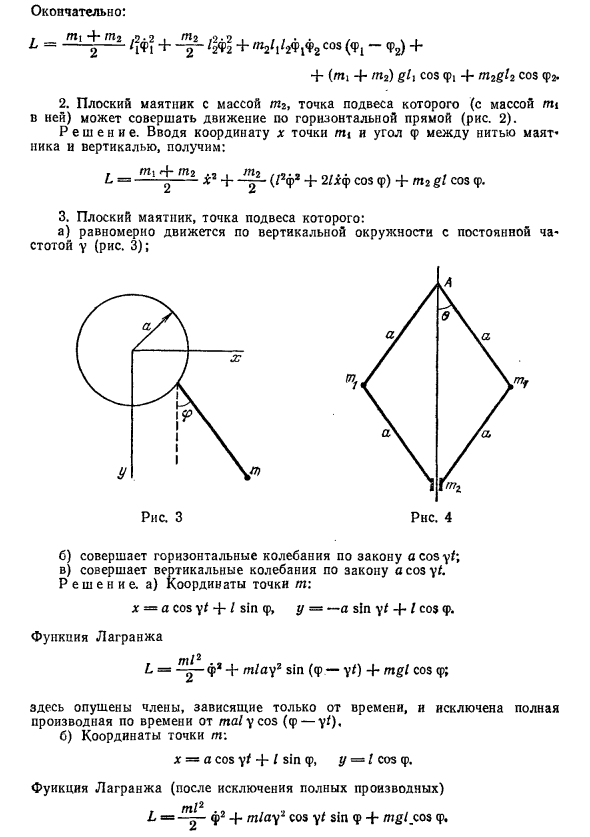
Для точки mi, Ti = ^ m i / ^ φ? , U = -m ig / icoscp i. Чтобы найти кинетическую энергию второй точки, Представляет собой декартовы координаты X2, г / 2 (Начало точки подвеса, ось Y-вертикальная Через угол) (пи, — (ZΦ + 21 φφCOS (p) — — 17l2gl cos (p. 3. Плоский маятник с точкой подвешивания: а) движется равномерно вдоль вертикального круга с постоянной частотой у (рисунок 3).

б) Выполнить горизонтальную вибрацию в соответствии с удобными правилами] в) выполнять вертикальную вибрацию в соответствии с законом Уютное. Решения. а) координаты точки mp: x = cosyt + / sin (p, y = -asinyt + I cos (p. Функция Лагранжа ml2 L = -ф2 + mlay2 sin (cp-yt) + mgl cos (p; Термины, которые зависят только от времени, здесь опущены Кроме того, общая производная по времени Марикос ((р-йт).

б) координаты точки m: х = уют + я грешу (р, у = лкос (с. Функция Лагранжа (после полного исключения Производные финансовые инструменты) ml2. 2 2 L = -ф + mlay cosy sin (p + mgl cos (p. в) Точно так же ml2. 2, 2, L = -ф + mlay cos cos (p + mgl cos (p. 4. Система 4 показана на рисунке; ​​Точка Ш2 Перемещается вдоль вертикальной оси, и вся система вращается с постоянной угловой скоростью Q4 Это ось. Решения.

Введите угол 0 между сегментом a и вертикалью и углом поворота (широкий угол системы p вокруг оси вращения). φ = Q. Для каждой точки mi, элемент смещения dti = a2 dQ2 + a2 sin2 0 dip2. В случае точки 777-2 расстояние от точки подвеса A составляет 2a cos 0, dh = -2asinQdQ. Функция Лагранжа L = mi a2 (02 + Q2 sin2 0) + 2m2a2 sin2 0 02 + 2ga (mi + m2) cos 0.

Функция лагранжа и уравнения лагранжа системы материальных точек

Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Решение уравнения ЛагранжаСкачать

Решение уравнения Лагранжа

Принцип наименьшего действия. Уравнения Лагранжа

Движение системы, имеющей s степеней свободы, можно описать посредством функций q 1 = 9i(i). q$ = qs(t)t определяющих зависимость обобщенных координат от времени t. Для краткости всю совокупность этих функций обозначим так:

Функция лагранжа и уравнения лагранжа системы материальных точек

Производные qa от обобщенных координат qQ = q0(t) по времени t называются обобщенными скоростями:

Функция лагранжа и уравнения лагранжа системы материальных точек

Используя функции (14.21), кинетическую

Функция лагранжа и уравнения лагранжа системы материальных точек Функция лагранжа и уравнения лагранжа системы материальных точек

Функцией Лагранжа (Жозеф Лагранж (1736 — 1813) — французский математик) называется функция

и потенциальную V = U(r. гуу, f) энергии системы можно выразить через обобщенные координаты и скорости и время I, т.е. представить их в виде

Функция лагранжа и уравнения лагранжа системы материальных точек

Уравнениями движения механической системы называются дифференциальные уравнения, решениями которых являются функции (14.23), описывающие движение этой системы. Для системы с идеальными связями, в которой действуют только потенциальные активные силы, уравнения движения могут быть получены из принципа наименьшего действия или принципа Гамильтона (Уильям Гамильтон (1805 — 1865) — ирландский математик и физик).

Пусть q = q(t) есть произвольная непрерывно дифференцируемая функция, удовлетворяющая условиям

Функция лагранжа и уравнения лагранжа системы материальных точек

где qW и qW — значения обобщенных координат, характеризующие какие- то два положения 1 и 2 системы в пространстве. Функционал 5 от функции г (рис. 14.7). Такая система имеет только одну степень свободы. Будем описывать ее движение при помощи функции у? =

Функция лагранжа и уравнения лагранжа системы материальных точек

в качестве обобщенных координат этой системы декартовы координаты материальных точек и запишем функцию Лагранжа:

Функция лагранжа и уравнения лагранжа системы материальных точек

где 1А — момент инерции цилиндра относительно мгновенной оси вращения, — его угловая скорость. Момент инерции однородного цилиндра относительно оси, проходящей через его центр масс, согласно формуле (6.30) равен

Функция лагранжа и уравнения лагранжа системы материальных точек

Рис. Ц.1. Для этой системы угол ф есть обобщенная координата

С учетом того, что расстояние от центра масс до мгновенной оси вращения равно г, угловую скорость цилиндра найдем по формуле Эйлера

Видео:Классическая функция Лагранжа частицыСкачать

Классическая функция Лагранжа частицы

Теоретическая механика. Уравнения Лагранжа

В этой статье мы попробуем разобраться с такой темой, как «Уравнения Лагранжа». Вообще, уравнения Лагранжа довольно полезная штука, например, на их основе решаются задачи на малые колебания. В МГТУ им. Баумана в третьем семестре предлагается самостоятельное домашнее задание, в котором нужно записать уравнения Лагранжа для системы с двумя степенями свободы.

Итак, типовое задание выглядит так.

Функция лагранжа и уравнения лагранжа системы материальных точекПрежде чем броситься решать эту задачу, посмотрим на задание и проанализируем его. Есть призма 3, которая движется поступательно по горизонтальной плоскости без трения. В призме сделан паз 2, по которому движется шарик 1. Если вы помните темы прошлого семестра, то легко увидите, что шарик совершает сложное движение — переносное поступательное вместе с призмой 3 и относительное поступательное по пазу 2. Далее есть стержень 4, который соединяет призму и каток 5. Очевидно, что скорость центра катка С равна скорость призмы. Каток движется без скольжения, это важный момент. Движение системы описывается двумя обобщенными координатами, которые любезно выбрал для нас составитель задания.

Итак, приступим к решению.

Поскольку обобщенных координат две (две степени свободы), система уравнений Лагранжа будет выглядеть так:

Функция лагранжа и уравнения лагранжа системы материальных точекРасчет начинаем с записи уравнений связи — выражаем скорости всех ключевых точек и тел, имеющих массу, через обобщенные координаты. Из сказанного ранее понятно, что нам понадобится линейная скорость призмы 3, линейная скорость катка 5, угловая скорость катка 5 и скорость шарика 1. С поступательным движением все просто

Функция лагранжа и уравнения лагранжа системы материальных точек

С угловой скоростью катка тоже все понятно. Так как проскальзывание отсутствует

Функция лагранжа и уравнения лагранжа системы материальных точек

Самое трудное — выразить скорость шарика 1. Как мы уже говорили, он совершает сложное движение, значит, его скорость складывается из относительной и переносной. Переносная — это скорость поступательного движения призмы 3. Относительное — скольжение вдоль паза 2, которое описано координатой S. Значит

Функция лагранжа и уравнения лагранжа системы материальных точек

Векторно складываем эти две скорости

Функция лагранжа и уравнения лагранжа системы материальных точек

Второе выражение здесь — это теорема косинусов. Если нанести все векторы на рисунок, станет понятно, почему так.

Функция лагранжа и уравнения лагранжа системы материальных точек

Определившись со скоростями, записываем выражение для кинетической энергии системы Т. Полная кинетическая энергия складывается из кинетических энергий всех тел, обладающих массой. То есть в нашем случае, тел 1, 3, 5.

Шарик 1 обладает энергией

Функция лагранжа и уравнения лагранжа системы материальных точек

Призма 3 движется поступательно

Функция лагранжа и уравнения лагранжа системы материальных точек

Каток 5 совершает плоское движение, так что его кинетическая энергия складывается из энергии поступательного и вращательного движений

Функция лагранжа и уравнения лагранжа системы материальных точек

Полная кинетическая энергия системы

Функция лагранжа и уравнения лагранжа системы материальных точек

Для записи уравнений Лагранжа это выражение нужно несколько раз продифференцировать.

Сначала по координате x. Частные производные

Функция лагранжа и уравнения лагранжа системы материальных точек

Производную по x с точкой дифференцируем по времени

Функция лагранжа и уравнения лагранжа системы материальных точек

Теперь то же самое по координате S. Частные производные

Функция лагранжа и уравнения лагранжа системы материальных точек

Производная по времени

Функция лагранжа и уравнения лагранжа системы материальных точек

Левая часть уравнений Лагранжа готова. Займемся правой частью. Для нее нужно посчитать обобщенные силы по каждой координате. Есть несколько способов это сделать, мы предпочитаем делать это через элементарную работу на малом приращении координаты. В общем случае формула выглядит так

Функция лагранжа и уравнения лагранжа системы материальных точек

На практике это применяется следующим образом. Сначала нанесем на рисунок все действующие силы. В нашем случае это сила упругости пружины и силы тяжести.

Функция лагранжа и уравнения лагранжа системы материальных точек

Сначала считаем обобщенную силу по координате x. Для этого мысленно «замораживаем» координату S, и позволяем системе свободно двигаться по координате x. То есть шарик «приклеивается» к пазу 2, и внутри него никуда не движется. Все перемещение происходит по координате x. Очевидно, что сила упругости работу не совершает, так как ее длина не меняется. Очевидно, что силы тяжести работу не совершают, так как движение происходит горизонтально. Официальным языком это записывается так

Функция лагранжа и уравнения лагранжа системы материальных точек

Теперь обобщенная сила по координате S. Мысленно «замораживаем» координату x. Получается, что призма 3 вместе с пазом 2 и катком 5 стоит на месте, а внутри неподвижного паза движется шарик. Сила упругости совершает работу, также как и сила тяжести шарика 1. Пружина была растянута на величину статической деформации δ и дополнительно растянута на S в произвольный момент времени, то есть сила упругости равна с·(δ+S). Работа силы упругости отрицательна, так как пружина растягивается. Работа силы тяжести шарика 1 положительна, так как шарик движется вниз. Силы тяжести призмы 3 и катка 5 работу не совершают, так как эти тела покоятся. Получаем

Функция лагранжа и уравнения лагранжа системы материальных точек

Собственно, все. Собираем все посчитанные величины в уравнения Лагранжа и получаем систему дифференциальных уравнений, описывающих движение системы.

Функция лагранжа и уравнения лагранжа системы материальных точек

Для проверки можно посмотреть размерности, в обеих частях выражения размерности должны совпадать (обычно это ньютоны).

Конечно, разные задачи немного отличаются в ходе решения, но алгоритм всех задач примерно такой.

1) Определить число степеней свободы и выбрать обобщенные координаты

2) Записать уравнения связей

3) Записать выражение для кинетической энергии

4) Взять необходимые производные

5) Записать обобщенные силы по каждой координате

6) Записать уравнения Лагранжа

Если что-то не получается, не отчаивайтесь, мы всегда рады помочь.

🔥 Видео

Уравнение ЛагранжаСкачать

Уравнение Лагранжа

Уравнения Лагранжа второго родаСкачать

Уравнения Лагранжа второго рода

Принцип наименьшего действия #2 - Уравнение Эйлера-ЛагранжаСкачать

Принцип наименьшего действия #2 - Уравнение Эйлера-Лагранжа

Кулешов А. С. - Теоретическая механика. Семинары. Часть 3 -Уравнения Лагранжа для материальной точкиСкачать

Кулешов А. С. - Теоретическая механика. Семинары. Часть 3 -Уравнения Лагранжа для материальной точки

Теоретическая механика. Лекция №1: Уравнения ЛагранжаСкачать

Теоретическая механика. Лекция №1: Уравнения Лагранжа

Теормех. 2021-окт-15. Группа РФЗ. Уравнения Лагранжа.Скачать

Теормех. 2021-окт-15. Группа РФЗ. Уравнения Лагранжа.

Условный экстремум и функция ЛагранжаСкачать

Условный экстремум и функция Лагранжа

Уравнение Лагранжа для консервативных системСкачать

Уравнение Лагранжа для консервативных систем

Уравнения Лагранжа #1Скачать

Уравнения Лагранжа #1

Механическая система со связями. Идеальные связи и уравнения Лагранжа 1-го рода.Скачать

Механическая система со связями. Идеальные связи и уравнения Лагранжа 1-го рода.

Численное решение системы уравнений Лагранжа I родаСкачать

Численное решение системы уравнений Лагранжа I рода

Аналитическая механика | функционал Лагранжа | 1Скачать

Аналитическая механика | функционал Лагранжа | 1

Уравнения Лагранжа 2-го рода. Функция Лагранжа и законы сохранения обобщенного импульса и энергии.Скачать

Уравнения Лагранжа 2-го рода. Функция Лагранжа и законы сохранения обобщенного импульса и энергии.

Несвободное движение точки. Уравнение ЛагранжаСкачать

Несвободное движение точки. Уравнение Лагранжа

Дифференциальное уравнение Лагранжа II рода. Расчет механической системы.Скачать

Дифференциальное уравнение Лагранжа II рода. Расчет механической системы.
Поделиться или сохранить к себе: