Функциональная грамотность в теме решение уравнений

Открытый урок по алгебре в 8 классе по функциональной грамотности «решение квадратный уравнений по формуле корней». Урок проходил в форме презентации

Просмотр содержимого документа
«Открытый урок по алгебре в 8 классе по функциональной грамотности «решение квадратный уравнений по формуле корней»»

КГУ «Целинная средняя школа»

район имени Габита Мусрепова

Северо- Казахстанская область

Открытый урок алгебры в 8 классе по функциональной грамотности

« Решение квадратных уравнений по формуле корней»

Учитель математики : Гришкевич А. И.

Открытый урок алгебры в 8 классе

Тема урока: Решение квадратных уравнений по формуле корней.

Цель урока: обобщение и систематизация способов решения квадратных уравнений, ликвидация пробелов в знаниях и умениях учащихся.

Цель ученика: уметь применять полученные знания и умения с целью правильно, быстро и рационально решать квадратные уравнения.

1. продолжить формирование понятия о квадратных уравнениях и проверка уровня сформированности навыка решения квадратных уравнений по формуле корней;

2. развивать логическое мышление, интеллект, память, навыки быстрого вычисления,

3. способствовать воспитанию учеников средствами своего предмета;

Тип урока: урок обобщения знаний и умений.

Методы обучения: словесный, практический, частично-поисковый, проблемный, наглядный.

Оборудование: презентация, доска, таблица №8.

Прогнозируемый результат: учащиеся совершенствуют навыки решения квадратных уравнений.

1. Вводно-мотивационный этап.

2. Исследовательская работа по видам квадратных уравнений.

3. Квадратные уравнения при подготовке к ВОУД .

4. Межпредметная связь.

5. Практикум по решению уравнений

6. Постановка домашнего задания.

7. Выводы по уроку.

8. Рефлексивно-оценочный этап.

В течении всего урока будет проводится перекрёстный опрос по видам уравнений, формуле Д, формулах корней.

1. Водно-мотивационный этап

1. целеполагание (ученики+я)

2. эта тема очень важная в курсе математики, она является первой ступенькой в изучении сложного материала.

Логическая минутка по развитию логического мышления и концентрации внимания

2. Исследовательская работа по видам квадратных уравнений

Вывод: все виды квадратных уравнений нужно знать.

3. Квадратные уравнения при подготовке к ВОУД

1. Найдите отрицательный корень уравнения: 20х 2 +х -12=0

А) —

В) —

С) —

Д) —

2. Решите уравнение: 100х 2 -1 =0

С) 0,1

Д) 0,01

3. Решите уравнение: 4х 2 -2х =0

Вывод: все виды уравнений нужно уметь решать быстро и качественно.

Математическая переменка «Это интересно знать» или кто такой Литр?

4. Межпредметная связь .

Решив уравнение, вы получите название цветка. О нём в народе говорят так « Цветы ангельские, а когти дьявольские».

-2;

Вывод: теория уравнений интересовала не только математиков.

5. Практикум по решению уравнений .

1. Решите уравнение: =

2. При каких значениях переменной разность дробей равна их произведению.

Решение: — =

6у+12-у 2 +4у-6у=0 -у 2 +4у+12-0 │*(-1) у 2 -4у-12=0 у₁=6 у₂=-2- не подходит

Проверка для у=6 — = * 3 — = 2 = = = Ответ : 6

Математическая переменка « Это интересно знать или Точность – вежливость королей»

Вывод: квадратные уравнения можно решать и такими способами.

6. Постановка домашнего задания.

№ 137 (3;4) + повторить или доучить формулы Д и корней квадратного уравнения

7. Выводы по уроку

— Вот и подошёл к концу урок, посвящённый решению уравнений. Теория уравнений интересовала

и интересует математиков всех времён и народов , а нам нужно решать уравнения – качественно и быстро!

8. Рефлексивно- оценочный этап.

-Какое событие урока поразило вас своей неожиданностью?

— С какими моментами урока вы не согласны?

— Какие вопросы сегодняшнего разговора требуют доработки?

Зелёный цвет – 3 балла Жёлтый цвет — 4 балла Красный цвет – 5 баллов

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Конспект урока с элементами функциональной грамотности «Решение текстовых задач с помощью квадратных уравнений» 8 класс

урок с элементами функциональной математической грамотности

Просмотр содержимого документа
«Конспект урока с элементами функциональной грамотности «Решение текстовых задач с помощью квадратных уравнений» 8 класс»

Тема: Решение текстовых задач с помощью квадратных уравнений

• Организовать деятельность учащихся по формированию умений и навыков в решении задач на составление квадратных уравнений.

• образовательные:
• актуализировать необходимые теоретические знания по теме (квадратное уравнение, виды квадратных уравнений,
• способы решения квадратных уравнений, виды задач, алгоритм решения задач с помощью уравнения),
• научить учащихся решать задачи с помощью квадратных уравнений,
• показать возможности применения изученной темы в практической жизни.

• способствовать развитию общения как метода научного познания, аналитического мышления, смысловой памяти, внимания;
• развитию навыков умственного труда — планирование своей работы,
• поиск рациональных путей ее выполнения,
• развитию навыков критической оценки результатов.

Воспитание дисциплины мышления,

• культуры устной и письменной математической речи;
• эстетическое воспитание;
• воспитание самостоятельности;
• воспитание коммуникативной

Урок применения знаний.

Формы работы на уроке:

Индивидуальная и групповая.

1 . Организационный этап

2. Мотивация. Актуализация знаний.

3.Формирование умений и навыков.

4. Рефлексивно-оценочный этап.

• — В какой теме мы с вами сейчас работаем?
• Квадратные уравнения, дробно-рациональные уравнения. уравнения, приводимые к квадратным.

• -Где могут применяться уравнения?
• при решении текстовых задач в алгебре, при решении задач геометрии, физики и химии

• -А может ли умение решать уравнения пригодиться в практической жизни ?

• — С помощью каких уравнений вы уже решали задачи в математике?
• Линейных
• -А теперь мы научились решать квадратные уравнения. Сформулируйте тему урока
• Решение текстовых задач с помощью квадратных уравнений

• — На эту тему отводится 4 урока. Можем ли мы сразу приступить к решению задач на нашем 1 уроке по этой теме?
• Нет, надо вспомнить необходимый теоретический материал
• — Сформулируйте цель урока.
• — Какие знания, формулы нам пригодятся на сегодняшнем уроке?

. Разберите решение задачи 1 в тексте учебника, стр 69, запишите решение.

В квартире проектируется две комнаты одинаковой ширины. Длина первой комнаты в 1,5 раза больше её ширины, а длина второй комнаты 7,2м. Определите, какой ширины должны быть комнаты, если общая их площадь может быть 56,7м2?

Решение: х- ширина, длина 1 комнаты 1,5х,

площадь 1 комнаты равна

площадь второй комнаты равна 7,2х .

По условию задачи составляем уравнение:

Х= -9 — не подходит к условию задачи.

Сформулируйте ответы на вопросы:

• Связана ли решённая задача с практической жизнью?
• -Понятен алгоритм решения задачи на составление квадратного уравнения?

Приём «Карусель» /работа в группе/

• Решения оформляются в тетрадях.
• После решения задачи, члены одной группы знакомятся с решением этой же задачи другой группой, выражают согласие или несогласие с их решением.
• В процессе решения задач возможно обращение к учителю. Учитель отмечают правильность решения задач каждой группой.
• Выставляется суммативная оценка каждому члену группы.

• 1)Задача о мобильной связи.

В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе, если известно, что радиус Земли равен 6380 км. Какую высоту должна иметь вышка мобильной связи, поставленная в нашем городе, чтобы село Бутаково и Черемшанка попали в зону связи (расстояние от вышки до данных сел по прямой не больше 25 км.)?

• 2)Задача на работу.

Работая вместе, штукатуры выполняют задание за 6 часов. За сколько часов может выполнить задание каждый рабочий, если одному из них для выполнения всей работы потребуется на 5 часов больше, чем другому ?

3) Задача на движение /Транспортная задача/

Товарный поезд был задержан в пути на 12 минут, а затем на расстоянии 60км он наверстал потерянное время, увеличив скорость на 15 км/ч. С какой первоначальной скоростью ехал поезд?

• 1)Задача о мобильной связи.
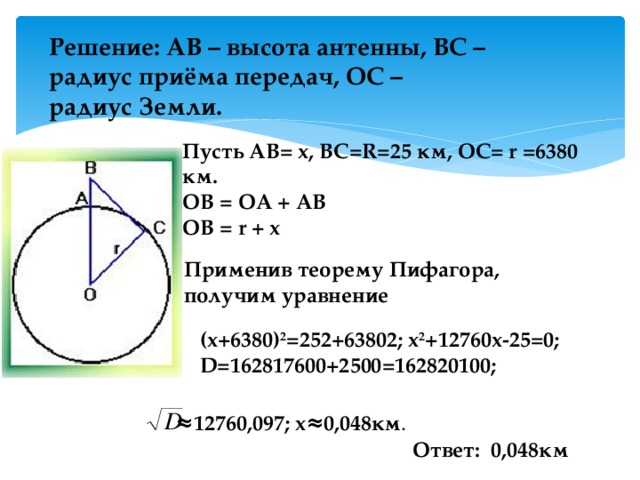
• В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе, если известно, что радиус Земли равен 6380 км. Какую высоту должна иметь вышка мобильной связи, поставленная в нашем городе, чтобы село Бутаково и Черемшанка попали в зону связи (расстояние от вышки до данных сел по прямой не больше 25 км.)?

Решение: АВ – высота антенны, ВС – радиус приёма передач, ОС – радиус Земли.

Пусть AB= x, BC=R=25 км, OC= r =6380 км.

Применив теорему Пифагора, получим уравнение

• какие понятия действительное имеют отношение к предложенной теме урока.

• Что нового Вы узнали сегодня?
• Что дляВас сталосамымудивительным, шокирующим, интересным, полезным сегодня?
• Что бы Вы сделали иначе?

• составить (найти) задачу с практическим содержанием, для решения которой потребуется составить квадратное уравнение.

• Спасибо за внимание!

Видео:Проверь свои знания по математике за 11 классСкачать

Формирование функциональной грамотности на уроках математики, на примерах заданий 1-5 ОГЭ

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Формирование функциональной грамотности на уроках математики на примерах заданий 1-5 ОГЭ.docx

Фахрутдинова Л.Т. МАОУ СОШ с. Первомайское Туймазинский р-н Башкортостан

Выступление РМО учителей математики

Фахрутдинова Лилия Тукбаевна

Учитель математики высшей категории

Формирование функциональной грамотности

на уроках математики

Хранение и передача знаний, навыков, норм и идеалов, образцов деятельности и поведения, социальных ценностей и ориентаций в системе образования осуществляется через учителя, поэтому к педагогической культуре учителя предъявляются высокие требования, одним из которых является функциональная грамотность.

В Федеральном государственном образовательном стандарте среднего общего образования (10–11е классы) (утвержденном приказом Минобрнауки России от 17 апреля 2012 г. № 413) указывается, что в рамках обучения математике (базовый уровень) необходимо добиться у учащихся сформированности представлений о роли и месте математики в современной научной картине мира; понимания математической сущности; понимания роли математики в формировании кругозора и функциональной грамотности для решения практических задач.

Функциональная грамотность – «способность человека решать стандартные жизненные задачи в различных сферах жизни и деятельности на основе прикладных знаний».

Функционально грамотная личность – это человек, ориентирующийся в мире и действующий в соответствии с общественными ценностями, ожиданиями и интересами.

Основные признаки функционально грамотной личности: это человек самостоятельный, познающий и умеющий жить среди людей, обладающий определёнными качествами, ключевыми компетенциями.

Под математической функциональной грамотностью следует подразумевать способность личности использовать приобретенные математические знания для решения задач в различных сферах.

На уроках математики дети учатся:

• выполнять математические расчеты для решения повседневных задач;
• рассуждать, делать выводы на основе информации, представленной в различных формах (в таблицах, диаграммах, на графиках), широко используемых в средствах массовой информации.

Образование является особой формой мышления, которая, подчиняясь диалектическим законам, поэтапно проводит обучающегося от незнания – к знанию, от владения знаниями – к их применению, а затем – к созданию новых знаний.

Именно поэтому, задания, призванные исследовать состояние математической грамотности учеников, имеют четко выраженную прикладную направленность и их решение предусматривает владение учащимися приемами деятельности прикладного характера.
Состояние математической грамотности учеников оценивается развитием “математической компетентности”. Математическая компетентность определяется как “сочетание математических знаний, умений, опыта и способностей человека”, которые обеспечивают решение разных проблем, нуждающихся в применении математики.

Многие идеи компетентностного подхода появились в результате изучения ситуации на рынке труда и в результате определения тех требований, которые складываются на рынке труда по отношению к работнику. Поэтому школа должна готовить своих учеников к переменам, развивая у них такие качества, как «мобильность, динамизм, конструктивность, инициативность, умение самостоятельно принимать решения»

Для формирования информационной компетентности необходимо использовать задачи содержащие информацию, представленную в различной форме (таблицах, диаграммах, графиках и т. д.). Вопрос задачи может быть сформулирован следующим образом: переведите в графическую (словесную) форму; если возможно, хотя бы приближенно опишите их математической формулой; сделайте вывод, наблюдается ли в этих данных какая-то закономерность и др.

Пример: Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.

Для формирования коммуникативной компетентности можно использовать групповую форму организации познавательной деятельности учащихся на уроках. Учащимся можно разделиться на несколько групп, каждая группа должна решить задачу предложенным способом и доказать правильность своего решения оставшимся группам.

Задача, которую можно решить, разделившись на группы.

№ 5 На плане (см. рисунок) изображена местность, прилегающая к озеру Круглому. Для удобства план нанесён на квадратную сетку, сторона каждого квадрата которой равна 500 м. Населённые пункты обозначены на плане жирными точками.

Рядом с озером Круглое находится болото, обозначенное на плане штриховкой. На болоте расположен хутор Камышино. От хутора Камышино проложена дорога к деревне Дубки, вокруг которой имеются дубовые рощи. Далее дорога идёт к селу Большое, расположенному по другую сторону озера от хутора Камышино. Село Большое соединено также дорогой с деревней Малая, обозначенной на плане цифрой 7. Деревня Малая, в свою очередь, соединена дорогой с деревней Дальней (отмечена цифрой 4). Преобладающая часть изображённой на плане местности — это поля, используемые для выращивания злаков.

Сторона одной клетки равна 500 м. Значит, 2 км дороги из хутора Камышино в деревню Дальняя будет проходить по болоту, а 0,5 км — по полю. Следовательно, стоимость дороги из хутора Камышино в деревню Дальняя равна

2*20+0,5*10=45 млн рублей.

Далее, 1 км дороги из хутора Камышино в деревню Малая будет проходить по болоту, а другие 3 км — по полю. Следовательно, стоимость дороги из хутора Камышино в деревню Малая равна

Таким образом, стоимость дороги из хутора Камышино в деревню Дальняя меньше и равна 45 млн рублей.

Для формирования исследовательской компетентности учащимся можно предложить задания, в которых необходимо исследовать все возможные варианты и сделать определенный вывод.

Пример: По периметру участка планируется установить забор. С двух сторон сквера будут два входа. При обсуждении, каким должен быть забор, рассматривалось два варианта: кованый или комбинированный. Цены на доставку оборудования и на установочные работы, а также стоимость изготовления одного погонного метра забора представлены в таблице. На сколько рублей общая стоимость кованного забора меньше общей стоимости комбинированного забора?

Найдём периметр сквера: 20*2*4=160 м.

Поскольку входы не учитываются, получаем160-2-4=154 м. Стоимость установки кованого забора равна:154*1000+3500+5130=162 630 рублей.

Стоимость установки комбинированного забора равна:

154*1300+3000+5300=208 500 рублей.

Разница в стоимости составляет 208 500-162 630=45 870 рублей.

Готовность к разрешению проблем формируется с помощью задач, в которых необходимо проанализировать предложенную ситуацию, поставить цель, спланировать результат, разработать алгоритм решения задачи, проанализировать результат.

Пример: Школьник Антон в среднем в месяц совершает 45 поездок в метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна. По истечении месяца Антон уедет из города и неиспользованные карточки обнуляются. Во сколько рублей обойдётся самый дешёвый вариант?

Формирование определенной системы математических знаний всегда было в центре внимания в математическом образовании. Объем этой системы является слишком большим с общеобразовательных позиций, а качество владения ими – недостаточно высоким. А главное, формирование этой системы знаний и умений не связана органически с формированием умений применять математику и стратегией решения задач.

Успешное выполнение контекстных заданий может быть обеспечено только при ориентации учебного процесса на решение подобных задач.

Чтобы повысить математическую грамотность учащихся, можно предложить учащимся самим составить задачи и уравнения, ребусы, кроссоворды, разноуровневые задания.

В связи с этим давайте все запомним одну математическую формулу, которая позволит сформировать у учащихся в процессе изучения математики и других дисциплин качества мышления, необходимые для полноценного функционирования человека в современном обществе.

«ОВЛАДЕНИЕ = УСВОЕНИЕ + ПРИМЕНЕНИЕ ЗНАНИЙ НА ПРАКТИКЕ»

Рассмотрим несколько примеров задач, для решения которых, необходима функциональная грамотность. Это, конечно же, первые пять задач ОГЭ по математике.

Тип задач «Участок»

На плане изображено домохозяйство по адресу: с. Корнеево, улица Парковая, д. 3 (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок слева от ворот находится веранда, отмеченная на плане цифрой 6. Площадь, занятая верандой, равна 9 кв. м.

Жилой дом находится в глубине территории. Помимо веранды и жилого дома, на участке имеются будка, имеющая наименьшую площадь на участке, и теплица, построенные на территории огорода (огород отмечен цифрой 2). Также в центре участка перед домом расположен пруд, а справа от него гараж.

Все дорожки внутри участка вымощены тротуарной плиткой размером 0,5 м × 0,5 м. Перед верандой имеется площадка, вымощенная такой же плиткой.

На участке планируется провести электричество.

№ 1 Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр .

Ответ.5714 (Слайд 13)

Тип задачи «Квартира» Слайды №20-25

Тип задачи «Автозаправочная станция» Слайды № 26-31

Функциональная грамотность становится фактором, содействующим развитию способностей школьников творчески мыслить и находить стандартные решения, умений выбирать профессиональный путь, использовать информационно-коммуникационные технологии в различных сферах жизнедеятельности, а также обучению на протяжении всей жизни.

Таким образом, задачи по формированию функциональной грамотности, в частности, математической грамотности обучающихся, возможно реализовать при условии оптимального сочетания учебного содержания базового уровня образования и дополнительных курсов, направленных на совершенствование прикладных математических умений, использующихся в различных жизненных ситуациях.

Спасибо за внимание!

Выбранный для просмотра документ Формирование функциональной грамотности на уроках математики.pptm

🔍 Видео

Повторяем решение уравнений. Полезно всем! Вебинар | МатематикаСкачать

Математика 6 класс (Урок№51 - Решение задач с помощью уравнений. Часть 1.)Скачать

Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать

11 класс, 27 урок, Общие методы решения уравненийСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Функциональная грамотность в примерахСкачать

Что такое функциональная грамотность?Скачать

Как решают уравнения в России и США!?Скачать

🚀Часть 1. Функциональные уравнения: Погружаемся глубже в математику🔮Скачать

Функциональная грамотностьСкачать

РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ. §3 алгебра 7 классСкачать

Система уравнений. Метод алгебраического сложенияСкачать

Д-13. Формирование функциональной грамотности обучающихсяСкачать

Не сдал ОГЭ Устное Собеседование shorts #shortsСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

функциональная грамотностьСкачать

Функциональная грамотность. Что использовать? Где применять? Когда формировать?Скачать