Функции заданной параметрически с помощью уравнений x sint y cost (8 видео)

Производная функции заданной параметрически онлайн

Пусть функция задана в виде параметрических уравнений (т.н. параметрическое задание функции):

где x ( t ) , y ( t ) — дифференцируемые функции и x ‘ ( t ) ≠ 0 . Тогда производная

определяется по формуле:

где — производная от параметрического уравнения y ( t ) по параметру t и — производная от параметрического уравнения x ( t ) , по параметру t .

Наш онлайн сервис найдет производную от параметрической функции с подробным решением. Пример подробного решения, выдаваемого нашим сервисом, можно посмотреть здесь .

Содержание

Функции заданной параметрически с помощью уравнений x sint y cost
Примеры кривых
Правила ввода выражений и функций
Где учитесь?
Функции, заданные параметрически, и их дифференцирование
Функции, заданные параметрически, и их дифференцирование
Примеры решения и задачи с методическими указаниями
💡 Видео

Видео:Математика Без Ху!ни. Производная функции, заданной параметрически.Скачать

Функции заданной параметрически с помощью уравнений x sint y cost

Построим график параметрической функции x=x(t) и y=y(t), которая задаёт прямую или кривую линию,
где параметр t лежит в промежутке [a, b],
и вы можете указать свои границы.
Задайте также функции x и y, зависящих от параметра.

Видео:14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать

Примеры кривых

Название кривой	Уравнение
Окружность
Спираль
Дельтоида
Астроида
Гипоциклоиды
Кардиоида
Нефроида
Эпициклоиды
Бабочка
Фигуры Лиссажу
Сердце

Правила ввода выражений и функций

3.14159.. e Число e — основание натурального логарифма, примерно равно

2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности

Видео:14.1. Касательная к параметрически заданной функцииСкачать

Где учитесь?

Для правильного составления решения, укажите:

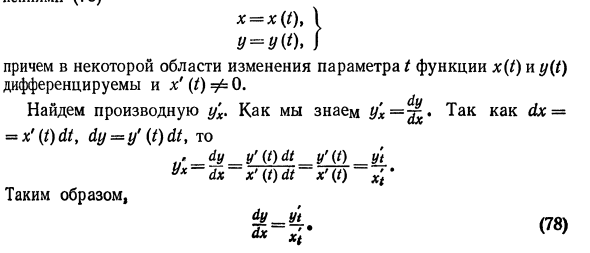
Видео:Решение найдите производные y′ и y″ параметрически заданной функции x=e^2t∙sint y= e^2t∙cost пример3Скачать

Функции, заданные параметрически, и их дифференцирование

Видео:20. Вторая производная параметрической функции, вывод формулы, примерСкачать

Функции, заданные параметрически, и их дифференцирование

Функции, задаваемые параметрами и их отличиями /. Параметрические обязанности и линии До сих пор рассматривались линейные уравнения на плоскости, которые непосредственно связывают текущие координаты этих точек. Тем не менее, другой метод определения линий часто используется. В этом методе текущие координаты x и y считаются функцией третьей переменной. Укажите две функции переменной /. (73) То же значение / считается.

Когда переменная t проходит через все значения области функции (73), точка My) описывает конкретную линию C в плоскости Ohu. Уравнение (73) называется параметрическим уравнением этой линии, а переменная / называется параметром. Предположим, что функция x = x (() имеет обратную функцию / = φ (:) :).

Тогда одно из этих значений t соответствует однозначному значению x и однозначному значению y, так что определенная точка M (x y) соответствует. Людмила Фирмаль

Подставляя эту функцию во второе выражение (73), выражение (74) y = y [Φ (A ‘)], Выразите y как функцию от x. Я согласен, что эта функция параметрически определяется уравнением (73). Переход от этих уравнений к уравнению (74) называется исключением параметров. При рассмотрении функциональности, Найдите вторую производную. Второй по определению FX.

Dx2 рф * ‘дх Функция параметра- = / (/), DY дх) дх d ^

Следует рассматривать как заданную функцию Параметрический: 1 * = «(/). J ■ ‘8 Следовательно,

= определяется уравнением (78) вместо y ду Должен быть заменен (А ты (79) «» Dar Пример 3. Найти вторую производную функции y, определенной параметрически. x = sin2 /, ^ y = sin2 /. ) Решения. В примере 1 первая производная была найдена, но рассматривают эту производную как параметрически определенную функцию. | = 2ctg2 /, | я Пой- ^ 7.

Видео:Производная от параметрически заданной функцииСкачать

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

Согласно уравнению (78) * = найти sin2 /, вторая производная dyV ‘

2 2 «в уравнении (79) Y /

(2 ctg _ sin * 2 /

__4

dx2 «» *

2 sin / cos / sin * 2 /’ Когда вы указываете параметр, исключение параметра не только не требуется, но и не всегда возможно на практике. Во многих случаях гораздо удобнее запрашивать разные значения для параметров и использовать уравнение (73) для вычисления соответствующих значений для аргументов x и y. Давайте посмотрим на некоторые примеры.

Пример 1.Декартовы координаты x и y этой точки выражаются полярным радиусом r-R и полярным углом. , §3, пункт 3): x = Rcostt y = Rs nt. ((7 ° Уравнение (75) называется параметрическим круговым уравнением. Эти параметры являются полярным углом / и варьируются от 0 до 2n. Если уравнение (75) возводится в квадрат и заканчивается для каждого члена, тождество устраняется тождеством cos2 // fsin2 / = 1, а круговое уравнение в декартовой системе координат xx + y2z = R * f определяет две основные функции вы: И tj- * / R2-A2’2. Каждая из этих функций определяется параметрически уравнением (75), но диапазон изменения параметров для этих функций различен.

Пусть M — любая точка на окружности с центром в начале координат и радиусе R. Людмила Фирмаль

Их первый 0 я Кроме того, в конкретной области изменения параметра t функции x (t) и y (t) дифференцируемы и x ‘(/) Φ0. Найдите производную y’x. Как вы знаете, yx = ^ 6 * dx = = x ‘(t) dt, dy = y’ (t) dt, то > dy_y ‘(t) dt y’ (t) yt yx dx x ‘<t) dt x’ (0 x’t ‘ Вот так ты не поймешь / * 7о Уравнение (78) находит производную параметрически определенной функции.

Пример 1. Найти производную функции y от k, заданную параметрическим уравнением x = sin2 /, y = sin2 /. Решение. Из уравнения (78) dy_y’t _ (sin 2Q ‘_ 2cos21 0 0 dx to x; (sin54 /)’ 2 sin / cos / ^ 8 Пример 2. Найти касательные и циклоидальные нормальные уравнения (А = 1) x = / -sin ^ r / = 1-cos / / T

Y ‘решение в точке Ml (xr; yx), соответствующей значению параметра. Найти координаты контакта Mt (xx yv). т. , Зло зла зло. Зло | -2 *! = (/ -Sin /) / = zy = -2 — Sin-2- = -2- + 1 * зло yt = ( -cos /) = 1 — COS— = 1. • г Найти производную от уравнения (78), чтобы найти коэффициенты тангенса и нормального угла. dy_ (1-cos /) ‘_ sin t dx

Найти угловой коэффициент касательной к циклоиде в точке М. b-dJ-1- (sin / = —I * kas-